问题描述

最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由结点和路径组成的）中两结点之间的最短路径。在最短路径上的各个顶点之间的路径也是各个顶点之间的最短路径

迪杰斯特拉算法

#define MAXEDGE 20
#define MAXVEX 20
#define INFINITYC 65535

我们需要三个辅助数组来存储相关的信息，分别是：

1. final数组，表示从V0到某个顶点Vi是否已经找到了最短路径，如果是final[i]=1
int final[MAXVEX] = {0};

2. W数组，表示从V0到某个顶点Vi的路径长度，final[i]=1时，w[i]表示最短路径的值。
int w[MAXVEX] = {INFINITYC};

3. P数组，表示路径中当前顶点的前驱顶点的下标，用于寻找最短路径，-1表示暂时还没有前驱顶点
int p[MAXVEX] = {-1};

思路

起点为V0，默认final[0] = 1, w[0] = 0, p[0] = -1
从v0出发，寻找v0的连通边，并更新数组w中对应的值。
在w中，寻找最小的权值min，以及对应的下标k，并且要求final[k]!=1。此时min即为从V0到Vk顶点的最小路径，更新p[k]=0，表示在V0到Vk的最短路径中，V0为Vk的前驱顶点，同时更新final[k]=1，我们根据p数组可以打印出V0到Vk的最短路径。
找到Vk对应的连通边，更新w中对应的值，因为V0通过Vk也可以访问到Vk的连通顶点，需要注意的是，可能存在某个顶点Vi，V0到Vi已经有了路径，但是V0通过Vk再到Vi的路径比较短，此时我们需要取最短的值。
重复步骤3，寻找下一个最短路径。

证明

主要的疑问在于步骤3中，如何确定最小的权值min以及对应的下标k就是新的最短路径呢？

因为min是从V0可以到达的路径中最小的值，假设存在其他某一路径经过Vi也可以到达Vk，那么路径长度为w[i]+x，其中w[i]为V0到Vi的路径长度而x为Vi到Vk的路径长度，可知min<w[i]+x，因为min<w[i]。

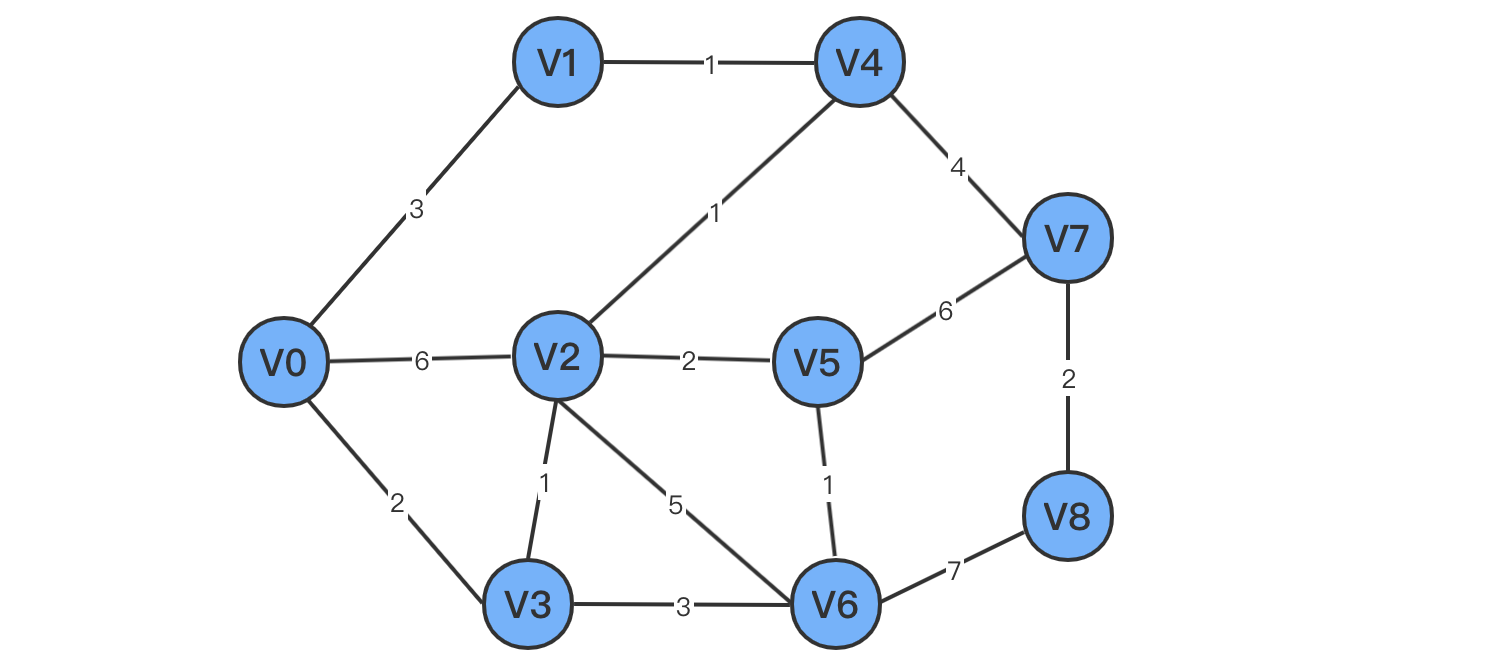
以上图为例

初始化数组final、w、p，默认V0已经有了最短路径，更新w、p中对应的值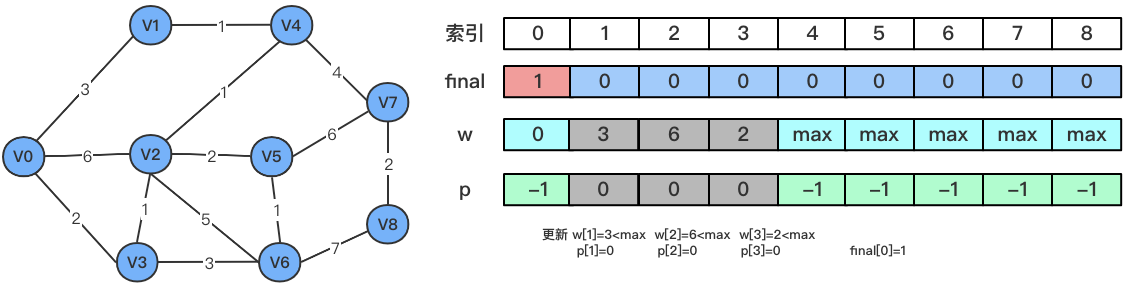
在w数组中找到路径最短同时没有找到最短路径的顶点V3，更新对应数组中的值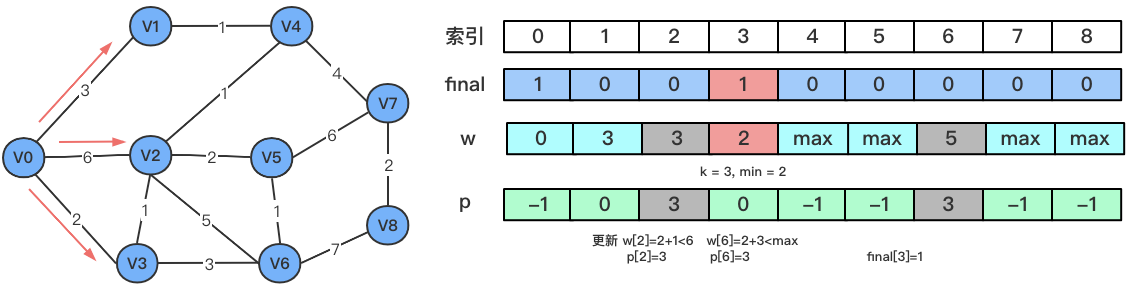
依次类推，找到V1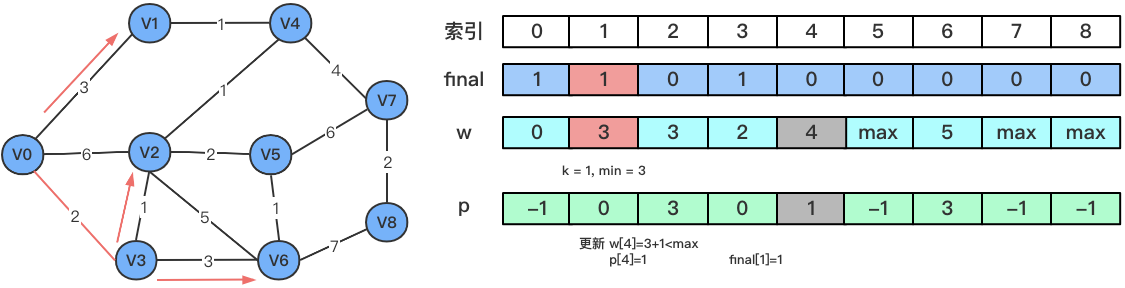
找到V2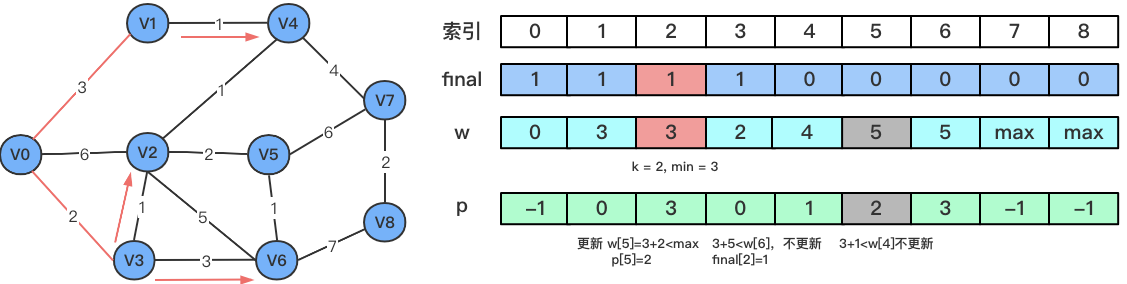
找到V4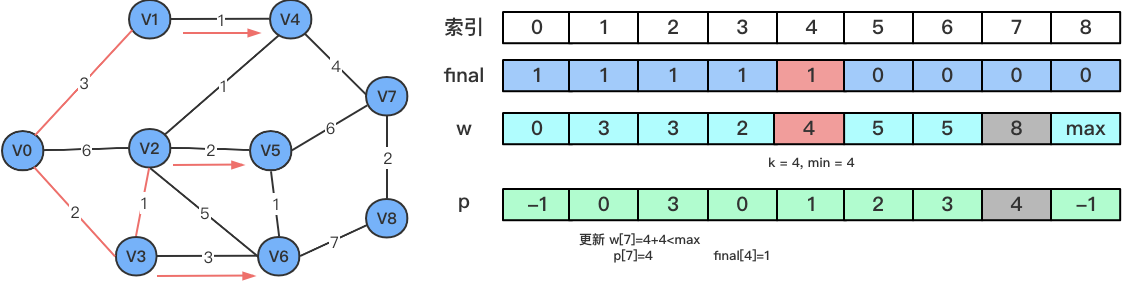
找到V5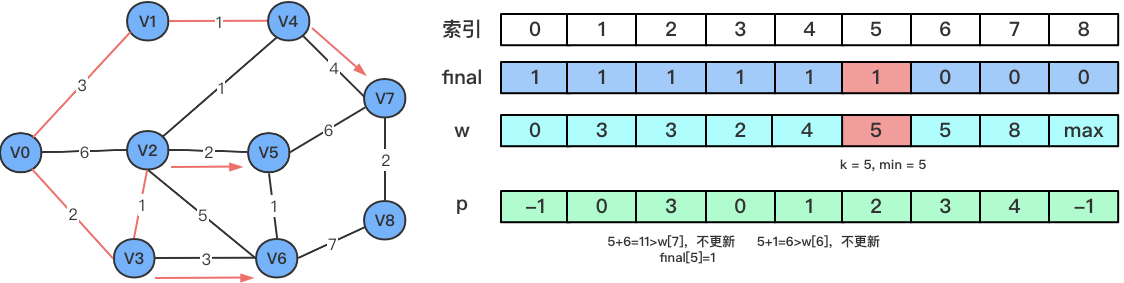
找到V6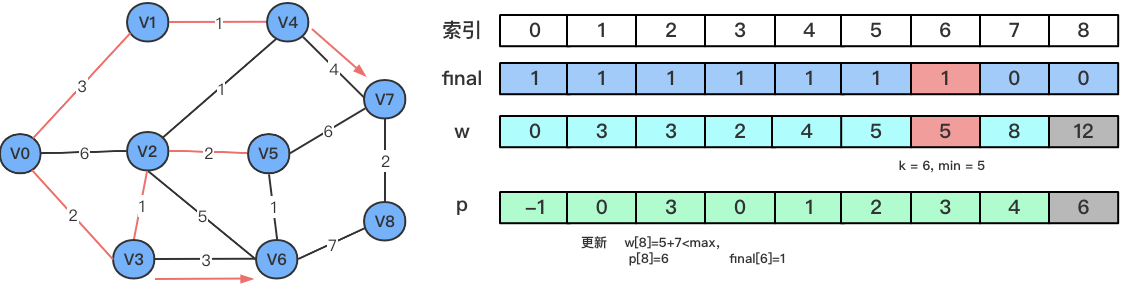
找到V7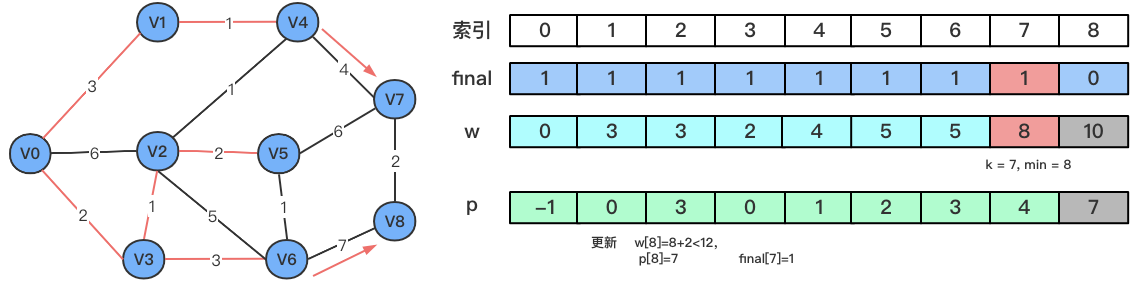
此时只剩最后一个顶点，其实已经找到了最短路径。代码

void ShortestPath_Dijkstra_1(MGraph G) {
    int final[MAXVEX] = {0};
    int w[MAXVEX];
    int p[MAXVEX];
    
    final[0] = 1;
    //初始化路径数组p
    for(int i = 1; i < G.numVertexes; i++) {
        w[i] = G.arc[0][i];
        if(G.arc[0][i] < INFINITYC) {
            p[i] = 0;
        }else {
            p[i] = -1;
        }
    }
    p[0] = -1;
    
    int min;
    int k = 0;
    for(int i = 1; i < G.numVertexes-1; i++) {
        min = INFINITYC;
        //找到w数组中路径最短并且还不属于最短路径的顶点
        for(int j = 1; j < G.numVertexes; j++) {
            if(w[j] < min && final[j] != 1) {
                k = j;
                min = w[j];
            }
        }
        final[k] = 1;
        //更新w数组的值以及p的路径
        for(int j = 0; j < G.numVertexes; j++) {
            if(final[j] != 1 && (min + G.arc[k][j]) < w[j]) {
                w[j] = min + G.arc[k][j];
                p[j] = k;
            }
        }
    }
    printf("最短路径路线:\n");
    for(int i=1;i<G.numVertexes;++i)
    {
        printf("v0 -> v%d : ",i);
        int j=i;
        while(p[j]!=-1)
        {
            printf("%d ",p[j]);
            j=p[j];
        }
        printf("\n");
    }
    printf("\n最短路径权值和\n");
    for(int i=1;i<G.numVertexes;++i)
        printf("v%d -> v%d : %d \n",G.vexs[0],G.vexs[i],w[i]);
    
    printf("\n");
}

Floyd算法

思路

假设图有n+1个顶点，在顶点Vi和Vj的最短路径T(i,j)上，必然存在某一点Vk(可能为V0到Vn的任意点)，将路径T分为了路径T(i,k)和T(k,j)。那么可以得到如下方程：

T(i,j) = min(T(i,k)+T(k,j))  0<=k<=n
我们还需要一个辅助数组P来记录中转顶点
P[i][j] = P[i][k];

代码

void ShortestPath_Floyd_1(MGraph G) {
    int T[G.numVertexes][G.numVertexes];
    int P[G.numVertexes][G.numVertexes];
    
    for(int i = 0; i < G.numVertexes; i++) {
        for(int j = 0; j < G.numVertexes; j++) {
            T[i][j] = G.arc[i][j];
            P[i][j] = j;
        }
    }
    //此处需要注意的是：k的循环顺序不能改变
    //另外需要记录的是P[i][k]，保证对应的值是路径的第一个顶点，记录k也可以，不过后面打印路径的时候比较麻烦。
    for(int k = 0; k < G.numVertexes; k++) {
        for(int i = 0; i < G.numVertexes; i++) {
            for(int j = 0; j < G.numVertexes; j++) {
                if(T[i][j] > (T[i][k]+T[k][j])) {
                    T[i][j] = T[i][k]+T[k][j];
                    P[i][j] = P[i][k];
                }
            }
        }
    }
    
    printf("最短路径D数组\n");
    for(int i=0; i<G.numVertexes; ++i)
    {
        for(int j=0; j<G.numVertexes; ++j)
        {
            printf("%d\t",T[i][j]);
        }
        printf("\n");
    }
    //打印最终变换后的最短路径P数组
    printf("最短路径P数组\n");
    for(int i=0; i<G.numVertexes; ++i)
    {
        for(int j=0; j<G.numVertexes; ++j)
        {
            printf("%d ",P[i][j]);
        }
        printf("\n");
    }
    printf("各顶点间最短路径如下:\n");
    int k;
    for(int i=0; i<G.numVertexes; ++i)
    {
        for(int j=i+1; j<G.numVertexes; j++)
        {
            printf("v%d-v%d weight: %d ",i,j,T[i][j]);
            //获得第一个路径顶点下标
            k=P[i][j];
            //打印源点
            printf(" path: %d",i);
            //如果路径顶点下标不是终点
            while(k!=j)
            {
                //打印路径顶点
                printf(" -> %d",k);
                //获得下一个路径顶点下标
                k=P[k][j];
            }
            //打印终点
            printf(" -> %d\n",j);
        }
        printf("\n");
    }
}

数据结构与算法-Day14-最短路径

问题描述

迪杰斯特拉算法

Floyd算法