1 线索二叉树
1.1 介绍
在前面的章节中介绍了二叉树的结构及三种遍历方式的实现。二叉树的遍历本质上是将一个复杂的非线性型结构转换为线性结构的过程,使每个节点都有前驱和后继(首尾节点除外)。对于树结构而言,查找它的子结点是很方便的,而查找其前驱与后继(在某种遍历顺序中)只能通过遍历实现。为了更加容易地找到前驱与后继有两种方法:
- 在结点结构中增加前驱与后继的指针
这种方法增加了内容的开销,不可取。
- 利用树节点中空链指针,即空的左右子结点指针,来指向前驱与后继
对于 n 个结点的二叉树中,将存在 n + 1 个空链,充分利用这些空间可避免空间的浪费。
其中记录的前驱与后继称为线索,在二叉树的结点上加上线索的二叉树称为线索二叉树,对二叉树进行遍历(前序、中序、后序)使其变成线索二叉树的过程称为对二叉树进行线索化。
1.2 线索化
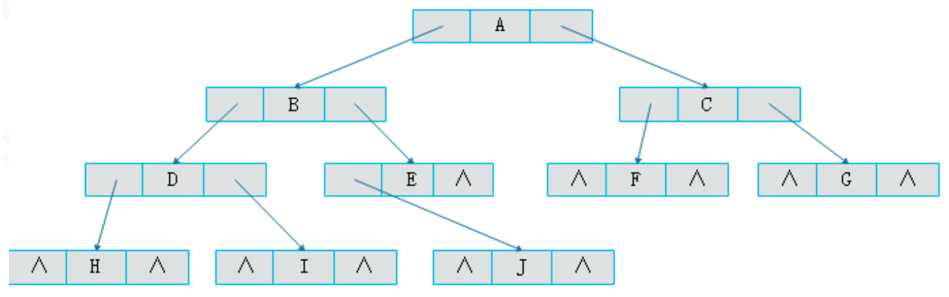
如图展示了一个二叉树的结构。一般情况下 ^ 处因为没有子结点,所以指针为空。线索化的过程就是充分利用这些空的指针,尽可能地添加遍历中的线索,提高遍历的效率。添加线索后的结构图如下所示:
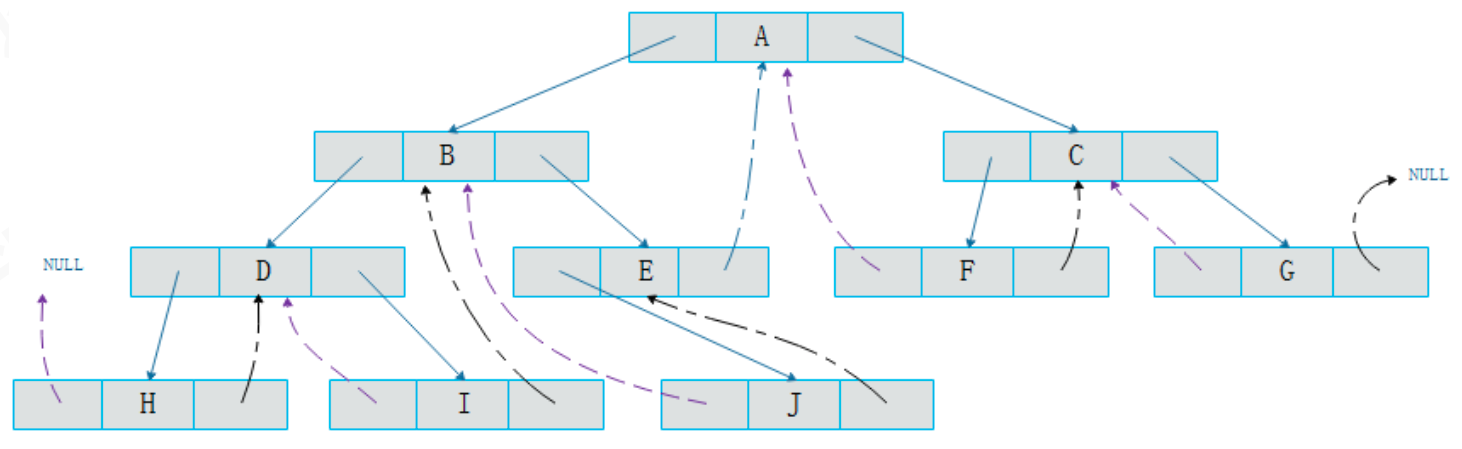
在原来二叉树的基础之上,将其中空的指针指向了遍历(前序)中的前驱或后继结点。当遍历到结点 I 时,一般情况下我们需要通过递归的方式才能继续走到后继结点 B。添加了线索后可以直接通过图中的线索 4 找到后继结点,节省了一定的开销。
在这种方式下,线索与子结点都是指针,如果不加辨认则将使结构混乱。所以去了区分二者,需要新建两个标志位来区分指针的用途。一般树节点的结构如下:

添加两个标志位之后结构如下:

1.2 双向链表结构
线索化的二叉树在进行遍历时,等价于操作一个双向链表结构。所以为了方便操作,可以添加一个头结点,这样做既可以从第一个节点顺序遍历,也可以从最后一个节点起倒序遍历。
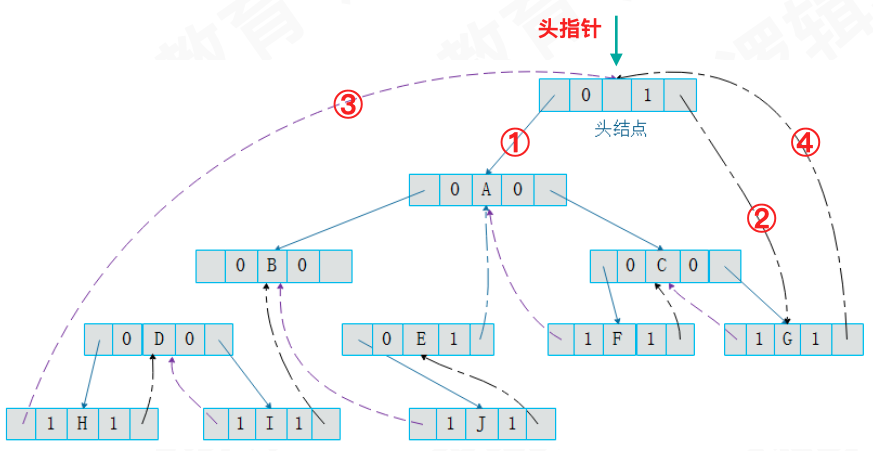
- 将头结点的左子树
lch指向树的根节点; - 将头结点的右子树
rch指向遍历过程中的最后一个节点; - 遍历过程中的第一个节点 H 的前驱指向头结点;
- 遍历过程中的最后一个节点 G 的后继指向头结点。
2 代码实现
2.1 结构
// 定义指针类型
typedef enum {
Link,
Thread,
} PointerType;
// 自定义数据元素类型
typedef char CElementType;
/// 定义线索二叉树节点
typedef struct ThreadBiTreeNode {
CElementType data; // 数据域
PointerType lpType, rpType; // 指针类型
struct ThreadBiTreeNode *lch, *rch; // 指针域
} *ThBiNodePtr;
比一般二叉树结点增加了两个标志位 lpType rpType 来表示指针的类型,可以通过枚举定义使代码更加清晰。
2.2 构建二叉树
// 序列化字符串
char *str = "ABDH#K###E##CFI###G#J##";
// 根据前序序列化字符串构建二叉树
static Status createThreadBiTree(ThBiNodePtr *t, char *str) {
static int index = 0;
CElementType data = str[index];
index++;
if (data == '#') {
*t = NULL;
return SUCCESS;
}
// 创建节点
*t = (ThBiNodePtr)malloc(sizeof(ThBiNodePtr));
(*t)->data = data;
// 构造左子树
createThreadBiTree(&(*t)->lch, str);
// 构造右子树
createThreadBiTree(&(*t)->rch, str);
return SUCCESS;
}
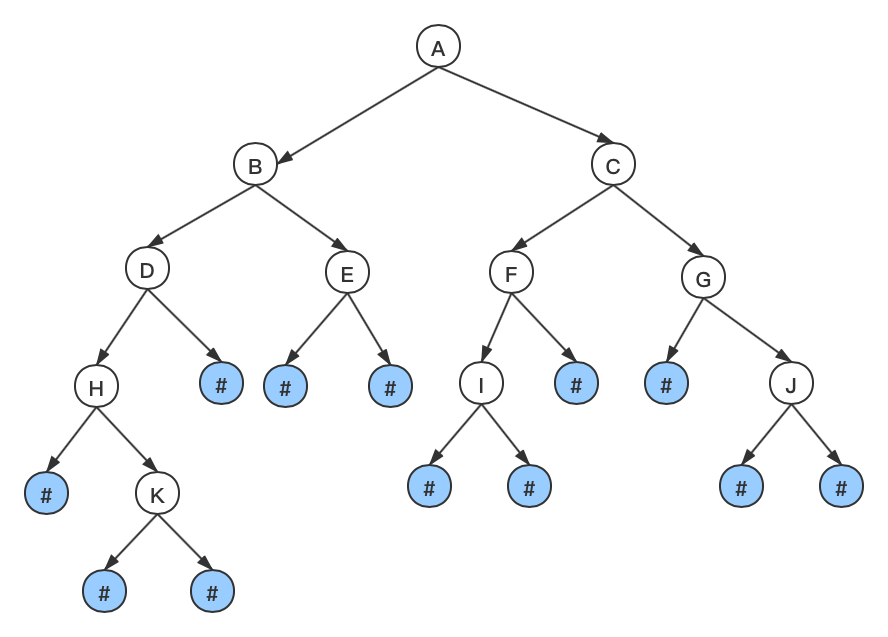
为方便使用,根据前序遍历的规则,构建了序列化的字符串,# 表示空结点,其他字符表示非空的节点。通过该字符串构建相应二叉树的结构。
前序遍历:ABDH#K###E##CFI###G#J##
2.3 线索化处理
// 中序遍历线索化二叉树
static void inOrderThreading(ThBiNodePtr t) {
if (!t) {
return;
}
// 1 递归线索化左子树
inOrderThreading(t->lch);
// 2 线索化自身结点
// 2.1 有无左子树
if (t->lch) {
// 有左子树,指针为 Link 类型
t->lpType = Link;
} else {
// 无左子树,指针为 Thread 类型
t->lpType = Thread;
// 指针指向前驱
t->lch = pre;
}
// 3 线索化 pre 结点
// 3.1 pre 有无右子树
if (pre->rch) {
// 有右子树,指针为 Link 类型
pre->rpType = Link;
} else {
// 无右子树,指针为 Thread 类型
pre->rpType = Thread;
// 设置 pre 的后继为当前节点
pre->rch = t;
}
// 4 将 pre 指向自身结点,线索化下一个结点
pre = t;
// 5 递归线索化右子树
inOrderThreading(t->rch);
}
// 使用头结点,中序遍历线索化二叉树
static Status inOrderThreadingWithHead(ThBiNodePtr *head, ThBiNodePtr t) {
// 1 创建头结点
*head = (ThBiNodePtr)malloc(sizeof(ThBiNodePtr));
// 左子树指向根结点
(*head)->lpType = Link;
// 右子树指向遍历中的最后一个结点,类型为线索类型
(*head)->rpType = Thread;
// 空树
if (!t) {
(*head)->lch = *head;
(*head)->rch = *head;
} else {
// 2 原根结点作为左子树
(*head)->lch = t;
// 3.1 初始化 pre 为头结点
pre = *head;
// 3.2 开始中序遍历线索化
inOrderThreading(t);
// 4 此时 pre 为最后一个节点
// head 右子树指向尾节点 pre
(*head)->rch = pre;
// 尾节点右子树指向头结点
pre->rpType = Thread;
pre->rch = *head;
}
return SUCCESS;
}
2.4 线索化遍历
/// 中序遍历,传入头结点 t
static Status inOrderTraverseWithThread(ThBiNodePtr head) {
// 0 获取首元根结点
ThBiNodePtr p = head->lch;
while (p != head) {
// 1 按照中序的规则,从结点的”最左“子树开始访问
while (p->lpType == Link) {
p = p->lch;
}
// 2 访问结点
printf("%c ", p->data);
// 3 访问下一个结点
// 3.1 如果右子树为线索,且后继不为头结点
while (p->rpType == Thread && p->rch != head) {
// 顺着线索依次访问结点
p = p->rch;
printf("%c ", p->data);
}
// 3.2 右子树不是线索,则按默认规则访问
p = p->rch;
}
return SUCCESS;
}
2.5 使用
int main() {
// 定义头结点和根结点
ThBiNodePtr head, t;
// 根据前序序列化字符串构建二叉树
char *str = "ABDH#K###E##CFI###G#J##";
printf("str = %s\n", str);
createThreadBiTree(&t, str);
// 添加头结点并线索化处理
inOrderThreadingWithHead(&head, t);
printf("线索化中序遍历:");
inOrderTraverseWithThread(head);
printf("\n");
return 0;
}
打印结果:
str = ABDH#K###E##CFI###G#J##
线索化中序遍历:H K D B E A I F C G J