数据结构和算法--线索二叉树

一、产生背景

正常二叉树结构：

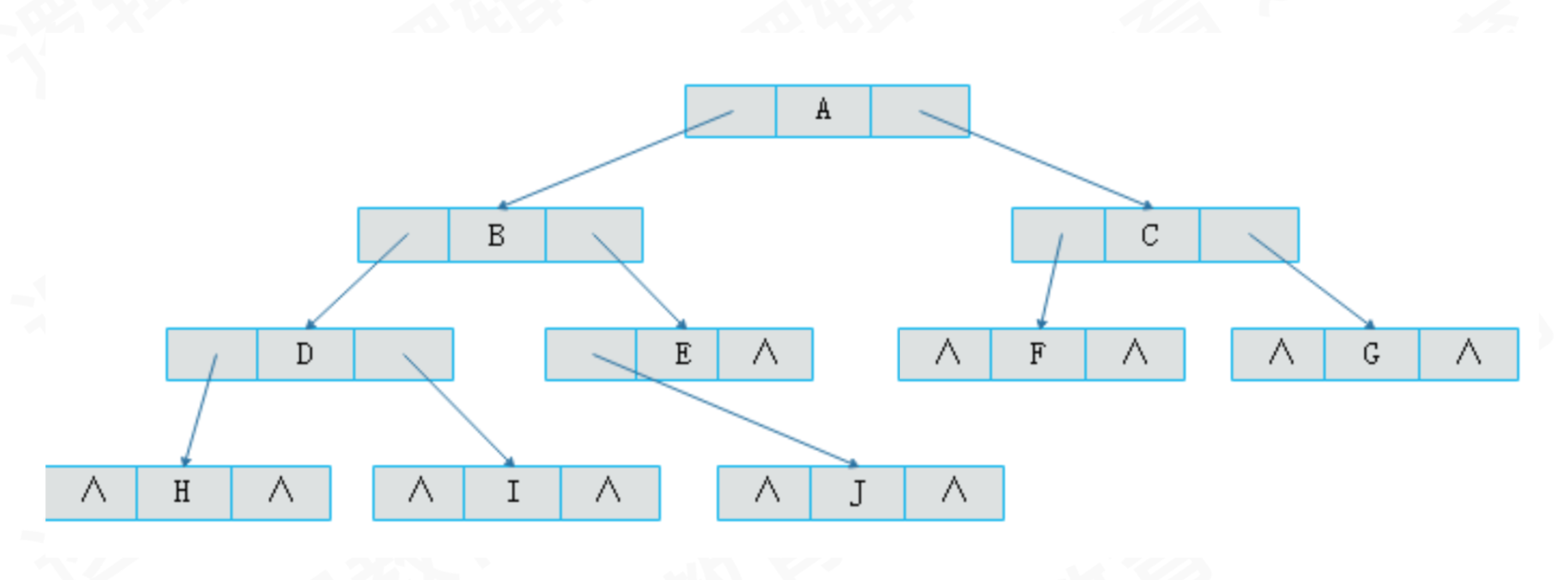
• 每个结点都有一个左指针、一个右指针，在叶子节点或者个别节点上左指针或者右指针为空，这样无形中浪费了存储空间，
• 所以这个时候我们引入了线索二叉树，我们可以将空出来的左指针指向该结点的前驱，空出来的右指针指向该结点的后继

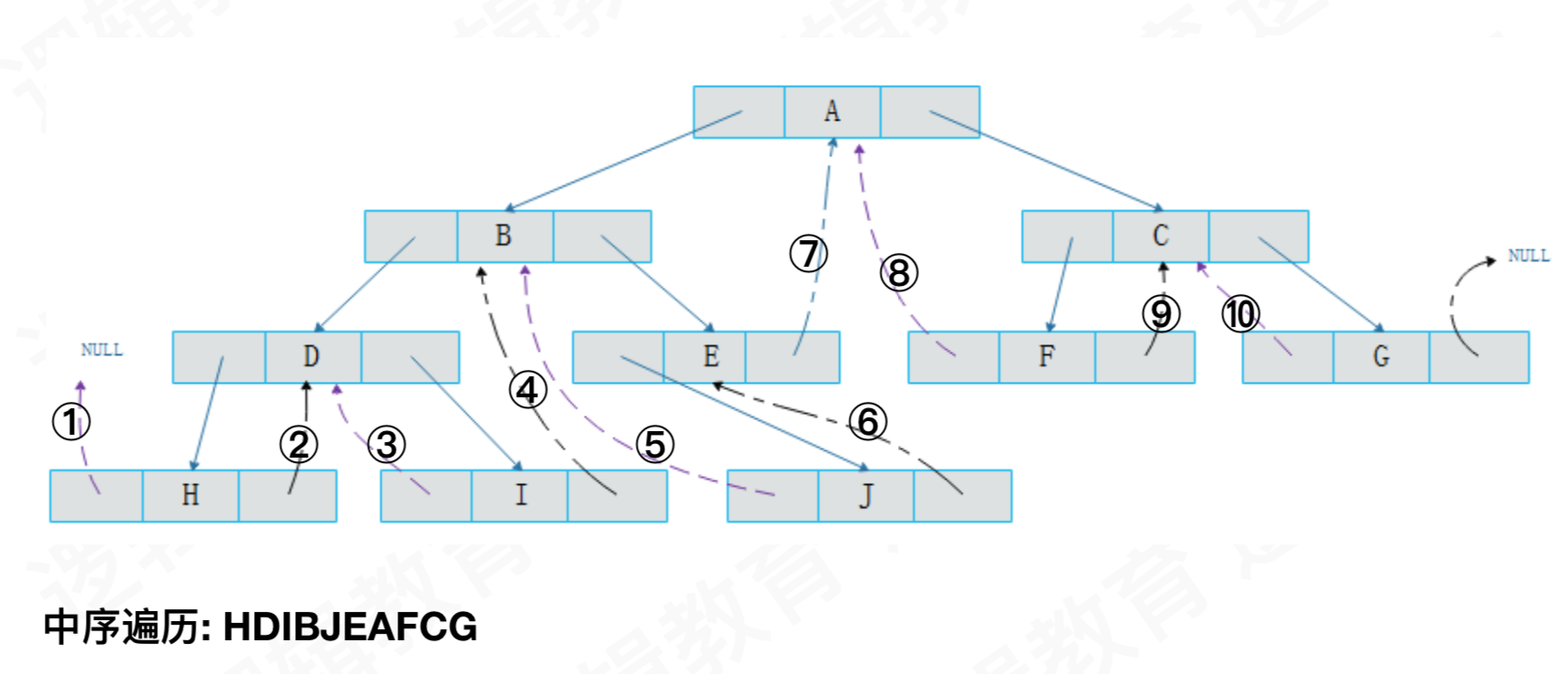
这个时候就出现问题，如何区分一个结点的左孩子指针指向的是左孩子还是前驱结点？

这个时候我们引入了tag标示，用来标示该指针指向的是孩子还是前驱或者后继

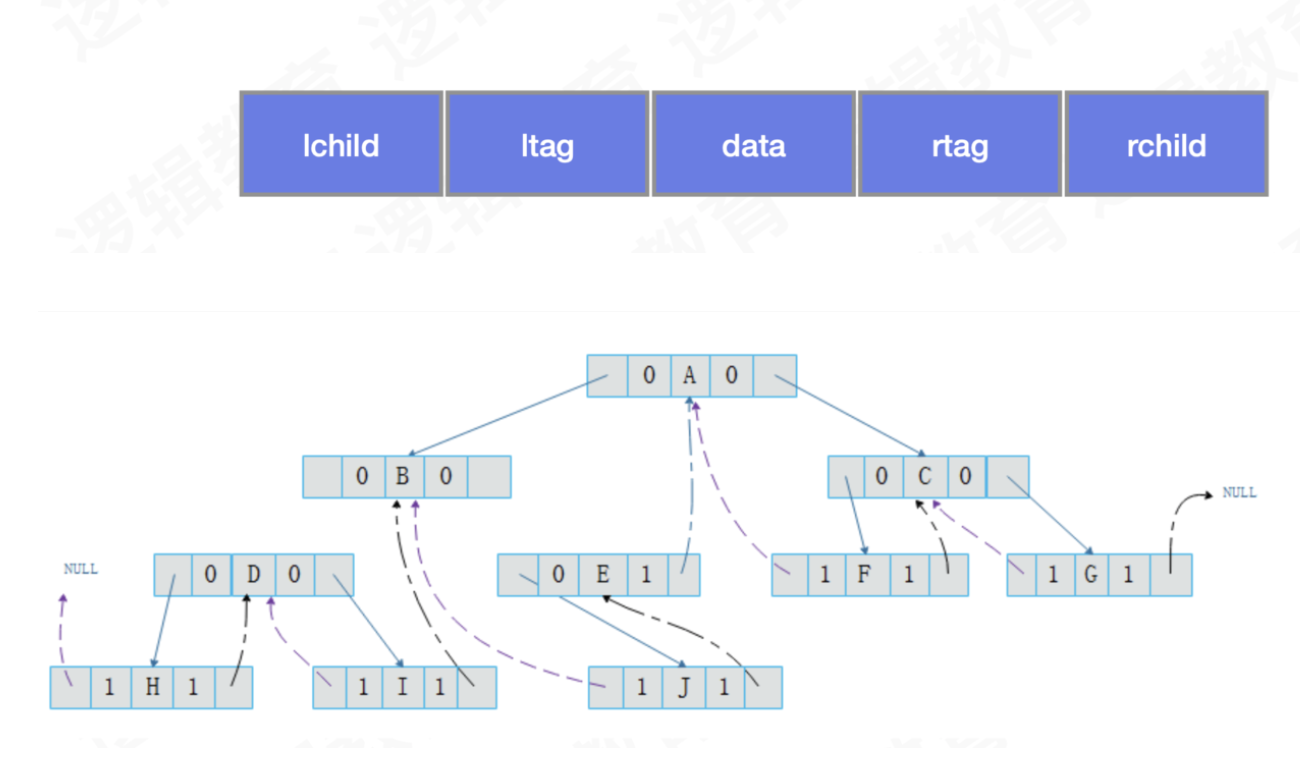
但是我们为什么不在每个结点上加上前驱和后继的指针的，这是因为线索二叉树的产生是为了将浪费的内存空间使用起来，如果每个结点都加上这样就会造成结构的存储密度大大降低，会浪费很多内存空间，这就跟线索二叉树产生的初衷发生悖论了，并且tag标示只是为了标示而创造的，并且tag标示占用的内存空间小

二、实现

1、结构

typedef char CElemType;
/* Link==0表示指向左右孩子指针, */
/* Thread==1表示指向前驱或后继的线索 */
typedef enum {Link,Thread} PointerTag;
/* 线索二叉树存储结点结构*/
typedef struct BiThrNode{
    //数据
    CElemType data;
    //左右孩子指针
    struct BiThrNode *lchild,*rchild;
    //左右标记
    PointerTag LTag;
    PointerTag RTag;
}BiThrNode,*BiThrTree;

以这种结点结构构成的二叉链表作为二叉树的存储结构，叫做线索链表。 其中指向结点前驱和后继的指针，叫做线索。加上线索的二叉树称之为线索二叉树。对二叉树以某种次序遍历使其变为线索二叉树的过程叫做线索化。

2、线索二叉树的操作

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100 /* 存储空间初始分配量 */

/* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef int Status;
typedef char CElemType;
/* 字符型以空格符为空 */
CElemType Nil='#';

二叉树构造

#pragma mark--二叉树构造
int indexs = 1;
typedef char String[24]; /*  0号单元存放串的长度 */
String str;
Status StrAssign(String T,char *chars)
{
    int i;
    if(strlen(chars)>MAXSIZE)
        return ERROR;
    else
    {
        T[0]=strlen(chars);
        for(i=1;i<=T[0];i++)
            T[i]=*(chars+i-1);
        return OK;
    }
}

/* Link==0表示指向左右孩子指针, */
/* Thread==1表示指向前驱或后继的线索 */
typedef enum {Link,Thread} PointerTag;

/* 线索二叉树存储结点结构*/
typedef struct BiThrNode{
    
    //数据
    CElemType data;
    
    //左右孩子指针
    struct BiThrNode *lchild,*rchild;
    
    //左右标记
    PointerTag LTag;
    PointerTag RTag;
    
}BiThrNode,*BiThrTree;

二叉树打印

/*
 8.1 打印
 */
Status visit(CElemType e)
{
    printf("%c ",e);
    return OK;
}

构造二叉树

/*
 8.3 构造二叉树
 按照前序输入线索二叉树结点的值,构造二叉树T
 */

Status CreateBiThrTree(BiThrTree *T){
    
    CElemType h;
    //scanf("%c",&h);
    //获取字符
    h = str[indexs++];
    
    if (h == Nil) {//如果字符为Nil说明树存储结束了
        *T = NULL;
    }else{
        //如果字符有值则创建第一个结点-跟结点
        *T = (BiThrTree)malloc(sizeof(BiThrNode));
        if (!*T) {
            exit(OVERFLOW);
        }
        //生成根结点(前序)，给节点赋值
        (*T)->data = h;
        
        //递归构造左子树，先将左子树创建完，再创建右子树，并将tag赋值为link
        CreateBiThrTree(&(*T)->lchild);
        //存在左孩子->将标记LTag设置为Link
        if ((*T)->lchild) (*T)->LTag = Link;
        
        //递归构造右子树
        CreateBiThrTree(&(*T)->rchild);
        //存在右孩子->将标记RTag设置为Link
        if ((*T)->rchild) (*T)->RTag = Link;
    }
    
    return OK;
}

中序遍历二叉树T, 将其中序线索化,Thrt指向头结点

1、中序遍历进行中序线索化

/*
 8.3 中序遍历二叉树T, 将其中序线索化,Thrt指向头结点
 通过对子树进行遍历处理的方式
 */

BiThrTree pre; /* 全局变量,始终指向刚刚访问过的结点 */
/* 中序遍历进行中序线索化*/
void InThreading(BiThrTree p){
    
    /*
     InThreading(p->lchild);
     .....
     InThreading(p->rchild);
     */
    if (p) {
        //递归左子树线索化
        InThreading(p->lchild);
        //无左孩子
        if (!p->lchild) {
            //前驱线索
            p->LTag = Thread;
            //左孩子指针指向前驱
            p->lchild  = pre;
        }else
        {
            p->LTag = Link;
        }
        
        //前驱没有右孩子
        if (!pre->rchild) {
            //后继线索
            pre->RTag = Thread;
            //前驱右孩子指针指向后继(当前结点p)
            pre->rchild = p;
        }else
        {
            pre->RTag = Link;
        }
        
        //保持pre指向p的前驱
        pre = p;
        //递归右子树线索化
        InThreading(p->rchild);
    }
}

2、中序遍历进行中序线索化

/*
 中序遍历二叉树T,并将其中序线索化,增加一个Thrt指向头结点
 */
Status InOrderThreading(BiThrTree *Thrt , BiThrTree T){
    //将二叉树T线索化，给T加一个头结点Thrt，Thrt左指针指向二叉树T的第一个节点，右指针指向二叉树的最后一个元素
    *Thrt=(BiThrTree)malloc(sizeof(BiThrNode));
    
    if (! *Thrt) {
        exit(OVERFLOW);
    }
    
    //建立头结点;
    (*Thrt)->LTag = Link;
    (*Thrt)->RTag = Thread;
    //右指针回指向
    (*Thrt)->rchild = (*Thrt);
    
    /* 若二叉树空,则左指针回指 */
    if (!T) {
        (*Thrt)->lchild=*Thrt;
    }else{
        
        (*Thrt)->lchild=T;
        pre=(*Thrt);
        
        //中序遍历进行中序线索化
        InThreading(T);
        
        //最后一个结点rchil 孩子
        pre->rchild = *Thrt;
        //最后一个结点线索化
        pre->RTag = Thread;
        (*Thrt)->rchild = pre;
        
    }
    return OK;
}

中序遍历二叉线索树T

/*中序遍历二叉线索树T*/
Status InOrderTraverse_Thr(BiThrTree T){
    BiThrTree p;
    p=T->lchild; /* p指向根结点 */
    while(p!=T)
    { /* 空树或遍历结束时,p==T */
        while(p->LTag==Link)
            p=p->lchild;
        if(!visit(p->data)) /* 访问其左子树为空的结点 */
            return ERROR;
        while(p->RTag==Thread&&p->rchild!=T)
        {
            p=p->rchild;
            visit(p->data); /* 访问后继结点 */
        }
        p=p->rchild;
    }
    
    return OK;
}

int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, 线索化二叉树!\n");
    BiThrTree H,T;
    
    //StrAssign(str,"ABDH#K###E##CFI###G#J##");
    StrAssign(str,"ABDH##I##EJ###CF##G##");
    
    CreateBiThrTree(&T); /* 按前序产生二叉树 */
    InOrderThreading(&H,T); /* 中序遍历,并中序线索化二叉树 */
    InOrderTraverse_Thr(H);
    printf("\n\n");
    return 0;
}