LeetCode每日一题221.最大正方形

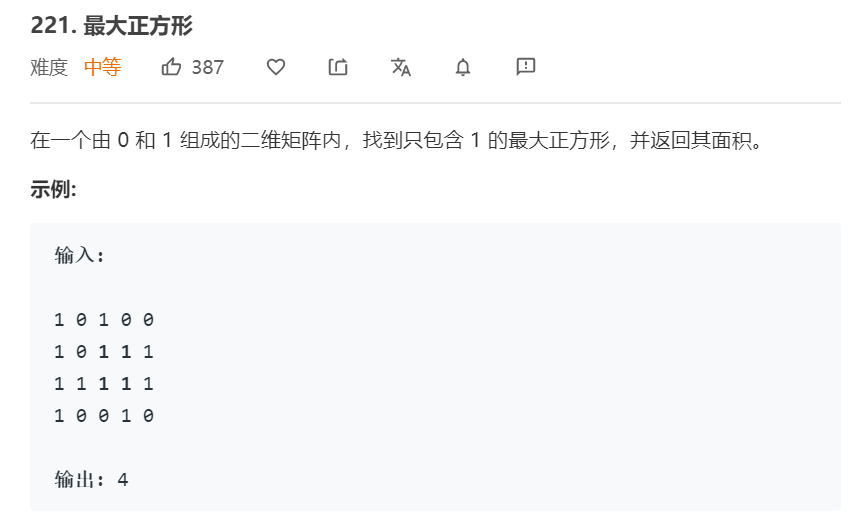
两种思路

• 暴力法遍历矩阵中的每一个1，然后寻找最大边长判断范围内的每个点是否都是1

public class Num221最大正方形 {
    public int maximalSquare(char[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }
        int row = matrix.length;
        int col = matrix[0].length;
        //初始化最大边长
        int maxLen = 0;
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                if (matrix[i][j] == '1') {
                    //如果有1，将最大边长置换成1
                    maxLen = Math.max(maxLen, 1);
                    //当前坐标下能遍历到的最大边长取决于两个边界距离的最小值
                    int curMaxLen = Math.min(row - i, col - j);
                    for (int k = 1; k < curMaxLen; k++) {
                        boolean flag = true;
                        //找到第一个对角线上不是1的元素，即是可能的最大边长记录下k
                        if (matrix[i + k][j + k] == '0') {
                            break;
                        }
                        //判断范围内的点是不是都是1，只有有一个不是1就break并把flag置成false
                        for (int m = 0; m < k; m++) {
                            if (matrix[i + k][j + m] == '0' || matrix[i + m][j + k] == '0') {
                                flag = false;
                                break;
                            }
                        }
                        //如果是满足要求的正方形，则将最大边长保留，进入下一次搜索
                        if (flag) {
                            maxLen = Math.max(maxLen, k + 1);
                        } else {
                            break;
                        }
                    }
                }

            }
        }
        //返回面积
        return maxLen * maxLen;
    }
}

• 方法二，考虑dp，dp[i][j]代表以(i,j)为右下角的点能构成正方形的最大边长,dp[i][j]的状态值取决于他上面，左边，和左上角三个值。

public class Num221最大正方形 {
    
    public static int maximalSquare2(char[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }
        int row = matrix.length;
        int col = matrix[0].length;
        int maxLen = 0;
        //dp[i][j]代表以(i,j)正方形右下角点能构成的最大边长是多少
        int[][] dp = new int[row][col];
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                //为0的就不需要判断了，默认值为0
                if (matrix[i][j] == '1') {
                    //初始化第一行和第一列
                    if (i == 0 || j == 0) {
                        dp[i][j] = 1;
                    } else {
                        //状态转移
                        dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;
                    }
                    maxLen = Math.max(maxLen, dp[i][j]);
                }
            }
        }
        return maxLen * maxLen;
    }
}