今天为大家带来三道关于求单数组最长上升xx的动态规划题目,都是leetcode上面的题目。本质都是一样的解法,只是在解决问题前需要对问题进行一定的转化。
第一题 leetcode-300《最长上升子序列》
这是一道很经典的动态规划题,也是三道中最容易的一题,不需要任何转换。我们可以将这个解题思路记作模板,使用这个模板去解决后面两道题目。
题目描述

还是按照之前的步骤,让我们一步步地解决这个问题:
I. 证明存在子问题和重叠子问题:
-
若给你一个只有一个数字的数组(数组A),那这个数组的最长上升子序列是多少呢?毫无疑问是1
-
那如果给你的数组是,数组A再加上另一个整数呢?也很容易,只需要看新加上的整数是否比数组A原先的元素大就可以了,大就返回2,小就还是返回1
通过上面这两个步骤,你是否已经体会到,我们是如何把一个更大的问题转化为子问题的呢?
很容易,看四个元素,我们只需要去看前三个元素的大小,与第四个元素比较就可以了。看三个元素同理,直到到达basecase(只有一个元素)
那重叠子问题在这道题中是如何产生的呢?
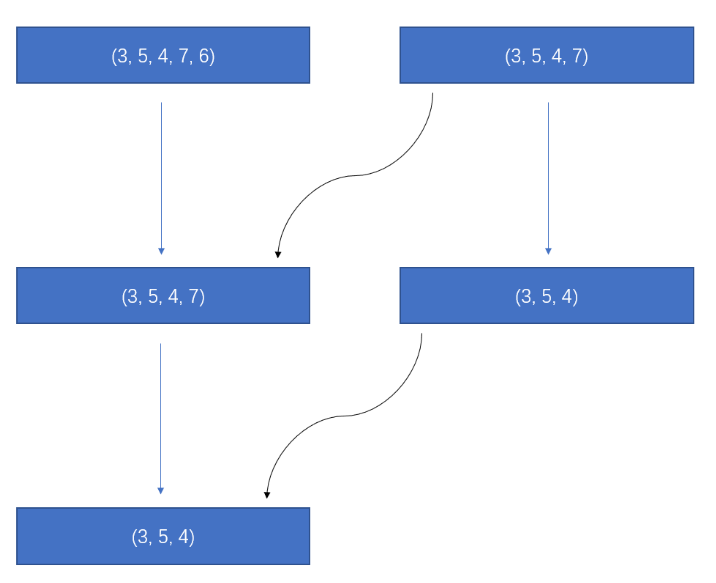
左侧是新增6这个元素之后,需要去判断前四个元素(3,5,4,7)的情况,而在此之前,我们在之前新增7这个元素的时候,就已经计算过(3,5,4,7)这个数组的情况,所以这时候就产生了重叠子问题。 (注意:我们是从整个数组只有3这一个元素,每次增加一个元素从而得到一个具有多个元素的数组的。)
II. 状态定义:
I中解释子问题和重叠子问题的过程中,其实本质就是一个状态到另一个状态的转移过程描述。即:(3,5,4,7,6)是一个状态,(3,5,4,7)是另一个状态。这两个状态之间有什么不同呢?
元素个数不同,更进一步地说,就是前一个状态比后一个状态多了一个元素,而其他部分都是相同的。再联系到我们的dp数组,很明显就可以用数组最后一个位置的索引来作为状态。
dp[index] = 数组从[0 - index]的最长上升子序列
需要注意的是,我这里的dp定义,还隐含了:index这个位置的元素必须在这个最长上升子序列当中。这是为了状态转移方程的书写方便,请读者们牢记这个定义,状态定义的不同会使我们状态转移方程的书写大相径庭。
III. 状态转移方程:
在开始书写方程之前,让我们再看看这个题目中的一些关键词,以及我们状态定义的关键词:
-
上升子序列
-
dp[index]为包含 array[index] 这个位置的最长上升子序列的长度
好了,现在让我们回顾I中,是如何将一个状态转移到另一个状态的。
就是把最后一个元素丢掉,去看前面的元素的情况。那么用一个循环就可以很容易地表达这种状态转移:
//求dp[index]
for(int cur = index; cur >= 0; cur --)
dp[index] = ...
再想想,有两个元素的时候,我们是如何判断最长上升子序列是1还是2?很明显,就是看第二个元素是否比第一个元素大就可以了!这里也一样,因为我们的dp[index]必须包含array[index]这个元素,所以我们要确保前面遍历到的元素不能比array[index]大。
这样,状态转移方程就可以很容易地写出来了:
dp[index] = Max(dp[i0], dp[i1], ..., dp[ik]) + 1;
// 其中 array[i] < array[index], i∈{i0, i1, ..., ik}
用我们上面的循环表示,就变成了这样:
for(int cur = index - 1; cur >= 0; cur --)
if(array[cur] < array[index])
dp[index] = Math.max(dp[index], dp[cur] + 1);
好了,到此为止,这道题就说完了,因为确实比较简单,所以说得比较快。下面是我的实现代码,供参考:
class Solution {
public int lengthOfLIS(int[] nums) {
int n = nums.length;
if(n == 0) return 0;
if(n == 1) return 1;
int[] dp = new int[n];
dp[0] = 1;
int res = Integer.MIN_VALUE;
for(int i = 1; i < n; i ++){
dp[i] = 1;
for(int j = i - 1; j >= 0; j--)
if(nums[i] > nums[j]){
dp[i] = Math.max(dp[i], dp[j] + 1);
}
res = Math.max(dp[i], res);
}
return res;
}
}
注意:
-
初始时,dp[0 -- n-1]都应该设置为1,因为dp[index]必须包含index处的元素,可能前面所有元素多比nums[index]要大
-
因为最长上升子序列,不一定包含整个数组的最后一个元素,而dp[n - 1]是包含最后一个元素的最长上升子序列长度,所以不应该直接返回dp[n - 1],而是取dp数组中的最大值返回
由于第二题和第三题跟第一题本质是一样的,只是需要一步转化,所以下面的我只给出问题转化过程的分析和代码,剩下动态规划的步骤读者请自行完成,可以当作是第一题的练习。
第二题 leetcode-646《最长数对链》
题目描述

很明显,这也是一个最长上升的问题,跟上面的第一题非常相似。
但是也有个很不一样的地方:第一题中给定的数组顺序是无法改变的, 我们只能按照给定的顺序,求出最长上升子序列,在这个子序列中,前面的元素在原数组nums中,也一定在后面元素的前面。
而此题则不一样,题目明确告诉我们,可以以任何顺序选择给出的数对来构造出最长数对链。
也就是,在此题中,给出的pairs是以下两种不同顺序的情况时,返回结果应该是相同的:

而在第一题中,如果给出的nums是一下这两种不同的数组,所求得的最长上升子序列必然是不同的:
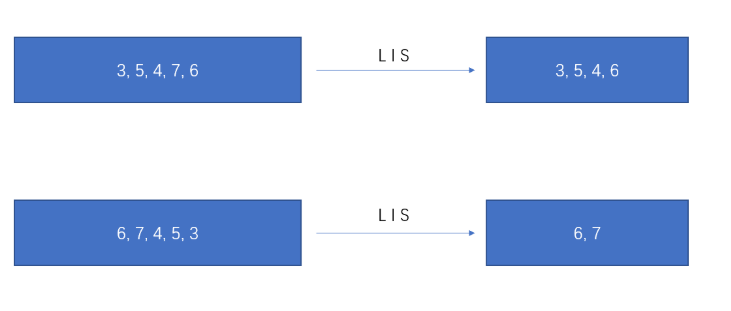
现在问题的关键是,我们是否可以通过对第二题中pairs进行一定的重排序,使其场景变得跟第一题一样呢?也就是说,我们要寻求一种排序方式,使得排序后的pairs数组,index + 1 位置的元素在最长上升数对链中必不可能出现在包含 index 位置的最长上升数对链中。(注意,按照我们第一题对dp数组的定义,dp[index]是包含pairs[index]的最长上升数对链的长度。如果pairs[index + 1]可能出现在pairs[index]前面,也就是pairs[index + 1]的b比pairs[index]的a要小,那我们此时的排序就是错的,因为 "pairs[index + 1] -> pairs[index]"也是一种可能的情况)
如果你读懂了上面那段话,那么排序方式就很明朗了,我们只需要按照pairs[index][1]进行排序就行了,也就是按照pairs[index]的数对(a, b)中的b,对整个pairs进行排序。
下面我简单证明一下上面这个排序方式的正确性:
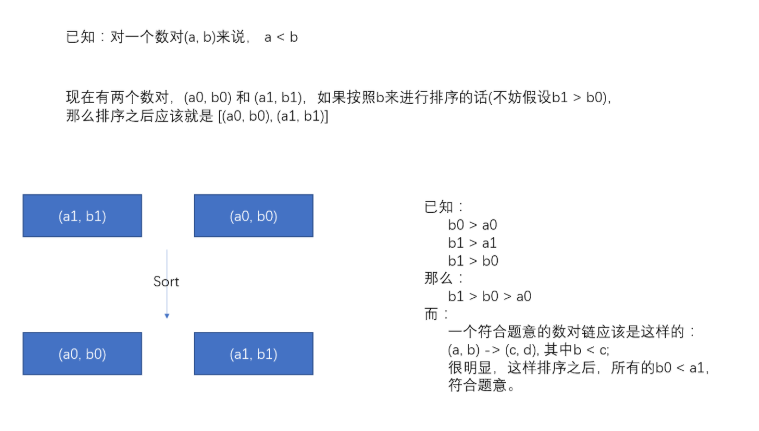
排好序之后,接下来就很简单了,按照第一题的思路做就可以了。下面给出我的代码,供参考:
public class LongestChain {
public int findLongestChain(int[][] pairs) {
int n = pairs.length;
Arrays.sort(pairs, (pair1, pair2) -> pair1[1] - pair2[1]);
int[] dp = new int[n];
dp[0] = 1;
int res = 1;
for(int i = 1; i < n; i ++){
dp[i] = 1;
for(int j = i - 1; j >= 0; j --)
if(pairs[i][0] > pairs[j][1])
dp[i] = Math.max(dp[i], dp[j] + 1);
res = Math.max(dp[i], res);
}
return res;
}
}
你会发现,整个代码除了有一步排序之外,跟第一题的过程几乎是一样的。
第三题 leetcode-1048《最长字符串链》
题目描述

整体来说,这道题其实是比第二题简单的,因为它的转化比起第二题来明显很多。
题目已经暗示了我们,后一个单词的长度要比前一个单词的长度长,所以我们这里的排序方式,就是按照字符串的长度,对整个words数组进行排序!
但是此题光是排序还是不够的,仔细看看题目,会发现此题要求后一个字符串必须是在前一个字符串的基础上添加一个字符可以获得的!
其实这很容易判断,只要遍历那个较短的字符串,看看是否能够通过一步操作到达那个比较长的字符串就行了。这个逻辑很简单,我就不多解释了。直接给出代码吧:
class Solution {
public int longestStrChain(String[] words) {
int n = words.length;
Arrays.sort(words, Comparator.comparingInt(String::length));
int[] dp = new int[n];
Arrays.fill(dp, 1);
int res = 1;
for(int i = 1; i < n; i ++) {
for (int j = i - 1; j >= 0; j--) {
String a = words[j];
String b = words[i];
if (a.length() + 1 < b.length()) break;
if (a.length() != b.length() && canBeChain(a, b))
dp[i] = Math.max(dp[i], dp[j] + 1);
}
res = Math.max(res, dp[i]);
}
return res;
}
private boolean canBeChain(String a, String b){
//默认a.length() < b.length()
boolean flag = false;
for(int i = 0; i < a.length(); i ++){
if(!flag && a.charAt(i) != b.charAt(i))
flag = true;
if(flag && a.charAt(i) != b.charAt(i + 1))
return false;
}
return true;
}
}
仔细看代码,你会发现,除了多了一步排序,和判断两个字符串是否"可达"之外,其余代码跟第一题的代码几乎是一样的。
(ps1:这里顺便可以说一下这种字符串"可达"问题,其实也是一个非常经典的动态规划问题,人称 “编辑距离”,在leetcode上也有相应题目,是leetcode的72号问题。)
(ps2:关于判断两个字符串是否一步可达,也可以使用最长公共子序列的技巧,判断两个字符串的公共子序列是否是较短的那个。而最长公共子序列本身也是非常经典的动态规划问题,在leetcode上也有相应的题目,是leetcode的1143号问题,感兴趣的读者可以去把这两个问题找来看看。)
(ps3:由于这两个问题过于经典,leetcode中的题解也是五花八门,要是有读者觉得有什么问题,可以直接去看题解。这两道题的题解里都有一个叫labuladong的大佬写了相应的题解,很清晰,有问题的读者可以看他的题解)
结语: 至此,我在这篇文章中想向大家介绍的三道题目已经全部说完了。值得一提的是,对于这样的一个最长上升子序列的问题,是有一种二分解法的,最后时间复杂度是O(nlogn),但是由于本文的目的是讲清楚动态规划,所以我不对这种太过胡里花哨的做法进行解释(为了大家的头发着想)。有兴趣的读者可以自行研究。