数据结构与算法之连通图的最小生成树

首先我们要知道什么是连通图的最小生成树，我们需要注意的是这个最小生成树不是树，它依然是图。

连通图的生成树概念

定义

一个连通图的生成树是一个极小的连通子图，它包含了图中所有的顶点，但只能构成图的n-1条边

生成树的条件

• 连通的
• 包含了所有的顶点
• 图中边的数量是n-1条

生成树的识别

• 不满足连通的条件

  
  

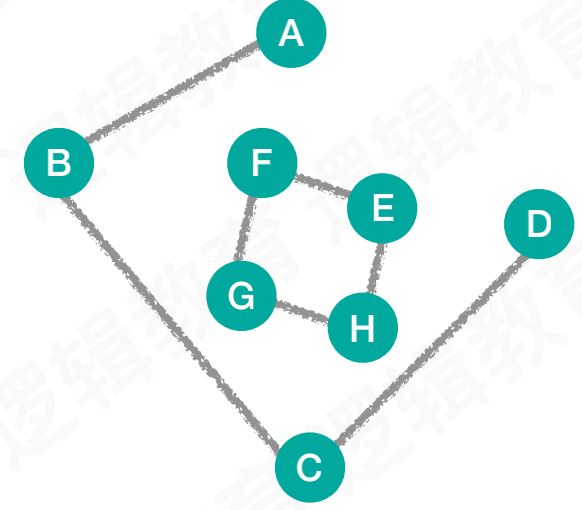
• 不满足包含所有顶点
• 不满足边数是n-1条

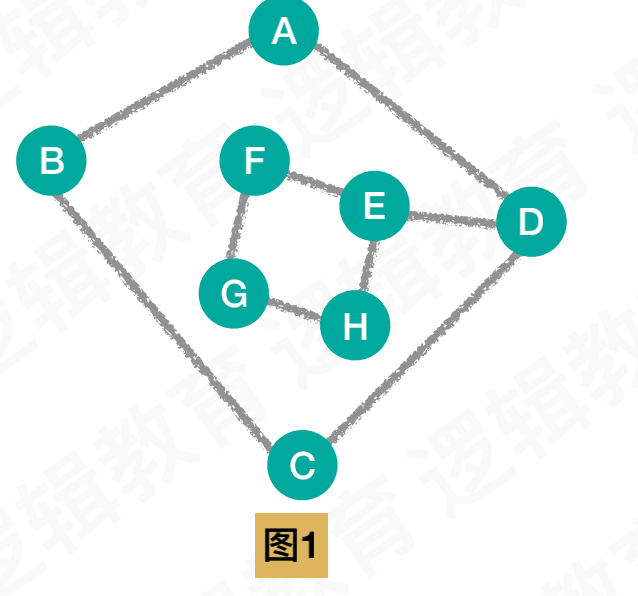
• 满足条件的生成树

  
  

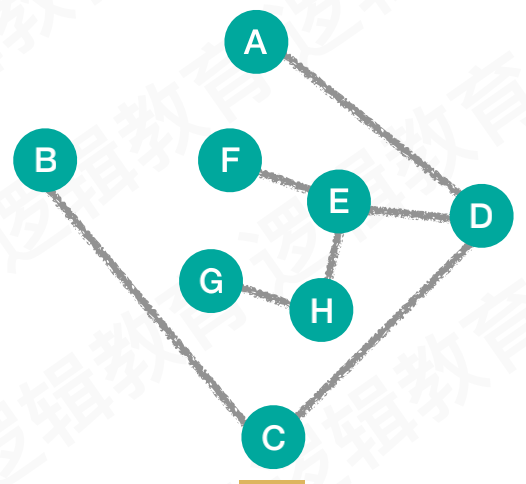
求解最小生成树的算法

假设有N个顶点，每个顶点连接的路径不一样，请设计一个算法快速找出能覆盖所有顶点的路径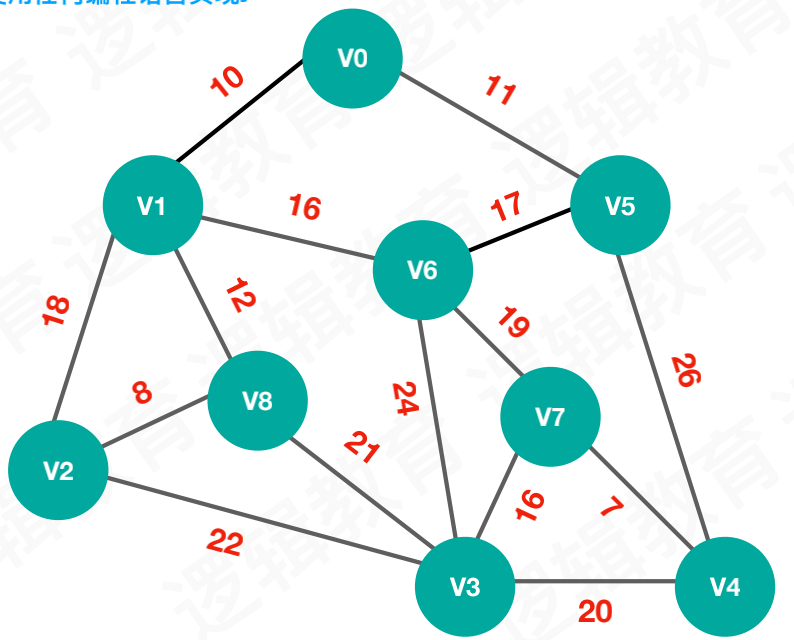

最小生成树的概念：构成连通图生成树的最小代价的生成树为最小生成树

Prim算法求解最小生成树

• 算法思路分析

  
  

• 核心代码实现

  /**
   时间复杂度O(n^2)，n为顶点的个数
   */
  void PrimSearch(MGraph Map){
      int min,i,j,k;
      int sum = 0;
      //定义保存相关顶点的数组，该数组的下标对应结束顶点，下标对应值是开始顶点，比如v0->v1则为：adjvex[1] = 0;
      int adjvex[MAXVEX];
      //定义保存相关顶点权值的数组,该数组的下标对应顶点，下标对应的值是该顶点的权值
      int lowcost[MAXVEX] = {INFINITYC};
      //我们默认从V0顶点开始加入生成树
      adjvex[0] = 0;
      //下标0表示顶点是V0，值0在这里表示已经加入到了生成树
      lowcost[0] = 0;
      //循环除v0顶点外的所有顶点
      for (i = 1; i<Map.numVertexes; i++) {
          //取出与v0顶点有关的权值
          lowcost[i] = Map.arc[0][i];
          //初始化相关顶点都起始位置都是v0顶点
          adjvex[i] = 0;
      }
      //循环除v0外的所有顶点
      for (i = 1; i<Map.numVertexes; i++) {
          //设置最小值为无穷
          min = INFINITYC;
          //每次循环j，k都重新设置
          j = 1;
          k = 0;
          //遍历剩余的顶点，查找最小权值的两个顶点
          while (j<Map.numVertexes) {
              //找到权值小于min并且没有加入到生成树的顶点
              if (lowcost[j] != 0 && lowcost[j] < min) {
                  //更新最小值
                  min = lowcost[j];
                  //记录最小值的顶点
                  k = j;
              }
              j++;
          }
          //打印路径以及权值,adjvex[k]是起点顶点，k是结束顶点
          printf("(v%d,v%d),权值为：%2d\n",adjvex[k],k,Map.arc[adjvex[k]][k]);
          sum += Map.arc[adjvex[k]][k];
          //设置k顶点已经加入了生成树
          lowcost[k] = 0;
          //循环遍历剩余顶点，更新adjvex数组以及lowcost数组
          for (j = 1; j<Map.numVertexes; j++) {
              //如果顶点j没有加入生成树并且与k顶点相关的权值小于min
              if (lowcost[j] != 0 && Map.arc[k][j] < lowcost[j]) {
                  lowcost[j] = Map.arc[k][j];
                  adjvex[j] = k;
              }
          }
      }
      printf("sum = %d\n",sum);
  }
  
  

Kruskal算法

• 算法思路分析

  
  

• 核心代码实现

  /* 对边集数组Edge结构的定义 */
  typedef struct {
      int begin;
      int end;
      int weight;
  }Edge ;
  #pragma mark - 给边数组排序
  void RankSort(Edge edges[], MGraph *Map){
      //对权值从小到大排序
      int tempValue;
      for (int i = 0; i<Map->numEdges; i++) {
          //j不能跟自己比所以要从i+1开始
          for (int j = i + 1; j<Map->numEdges; j++) {
              if (edges[i].weight > edges[j].weight) {
                  //交换begain
                  tempValue = edges[i].begin;
                  edges[i].begin = edges[j].begin;
                  edges[j].begin = tempValue;
                  //交换end
                  tempValue = edges[i].end;
                  edges[i].end = edges[j].end;
                  edges[j].end = tempValue;
                  //交换权值
                  tempValue = edges[i].weight;
                  edges[i].weight = edges[j].weight;
                  edges[j].weight = tempValue;
              }
          }
      }
      //打印下交换后的数据
      printf("交换后的数据为：\n");
      for (int i = 0; i<Map->numEdges; i++) {
          printf("(v%d,v%d)的权值为：%d\n",edges[i].begin,edges[i].end,edges[i].weight);
      }
  }
  #pragma mark - 查找父顶点
  int FindParent(int *parent, int result){
      while (parent[result]>0) {
          result = parent[result];
      }
      return result;
  }
  #pragma mark - Kruskal算法最小生成树
  void KruskalSearch(MGraph Map){
      //1、构建边数组
      int i,j,m,n;
      int k = 0;
      Edge edges[MAXVEX];
      for (i = 0; i<Map.numVertexes - 1; i++) {//最后一个顶点不需要了，否则第二层循环不会执行
          for (j = i + 1; j<Map.numVertexes; j++) {
              if (Map.arc[i][j] < INFINITYC) {
                  edges[k].begin = i;
                  edges[k].end = j;
                  edges[k].weight = Map.arc[i][j];
                  k++;
              }
          }
      }
      //对Map的边数组进行排序
      RankSort(edges, &Map);
      //定义parent数组,其中喜下标为起始顶点，下标的值为结束顶点，当下标值为0时表示没有下一个顶点了
      int parent[MAXVEX] = {0};
      int sum = 0;
      printf("最小生成树\n");
      for (i = 0; i<Map.numEdges; i++) {
          //获取begin、end信息
          //如果m == n则会有闭环
          n = FindParent(parent, edges[i].begin);
          m = FindParent(parent, edges[i].end);
          if (n != m) {//没有闭环
              //保存到parent数组中，此时改顶点已经在生成树中
              parent[n] = m;
              printf("(v%d,v%d),权值为：%2d\n",edges[i].begin,edges[i].end,edges[i].weight);
              sum += edges[i].weight;
          }
      }
      printf("sum = %d\n",sum);
  }