分类是人类时时刻刻在做的事情,比如我们收拾孩子的玩具的时候,需要辨认哪个是“玩沙子套装”的成员、哪些是图书,然后分类存放。
一些比较懒的人,希望让生活中尽量多的事情自动化。比如一个哥们,构建了一个分类装置,将两吨的乐高积木按照颜色、形状做了分类。分类装置的核心是一个训练好的神经网络。分类算法在生产和生活里的用处不止于此。
神经网络挺好的,本文介绍一下k最近邻算法(k-Nearest neighbor,kNN)。kNN是我确信自己学明白的第一个分类算法,它非常简单。
1kNN分类算法简介
1.1kNN分类算法的思想
kNN算法认为,具体的事物之间存在一定的相似性。举个例子,假设我和一只大熊猫的相似度是s1,我和赵本山的相似度是s2。除非大家抬杠,综合身高体重毛发等等特征,我和本山大叔显然更相似,即 s1< s2。
kNN算法认为,如果一个待分类样本,与类别(假设是A类)的代表性样本最像,相似程度超过了其他类别的代表性样本,那么,我们可以判定待分类样本的类别为A。
当然,实际操作的时候,我们用“距离”的远近来表示相似程度的大小:距离越远,相似度越低;距离越近,相似度越高。
1.2kNN算法的最简单形态-NN算法
假设我们要将10000个生物分为(人类,动物)两类,如果用最近邻算法(Nearest neighbor, NN)来完成这个任务,步骤是:
(1)请专家挑选1个人类(A类), 1个动物(B类);
(2)对于第i个生物,我们计算它与那个人类的距离,以及它与那个动物的距离,然后看那个距离更小,对应的类别就是这个生物的类别;
(3)重复(2)步,直到对所有生物分类完毕。
前面我们用纯语言的方式描述这个算法,对一些人比较合适,接下来用图形介绍一下,如图1-1。分类器会计算我离赵本山更近一点,还是离大熊猫更近一点,然后以离我更近的赵本山的类别,作为我的类别。
有的人看图学得快,有的人看文字学得快,有的人看公式学得快,大家平时可以注意一下哪种是最适合的。后面我们会有公式。
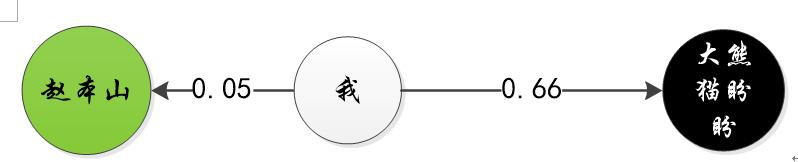
图1-1 最近邻分类器判断我是人类还是动物
1.3kNN分类算法的完整形态
1.2讲的分类器比较简单,只找了本山大叔和大熊猫作为分类依据,现在我们看完全体的kNN。我们请专家找4个人类,4个动物分别作为AB两类的代表性样本,如图1-2,这样既可以构建一个4-NN分类器。是的,kNN中的“k”是一个整数,它代表了我们选取的代表性样本的个数。
这一次,分类器需要计算我和赵本山等的平均距离,以及我和大熊猫组合的平均距离。我和前者的距离更小,因此我属于A类。
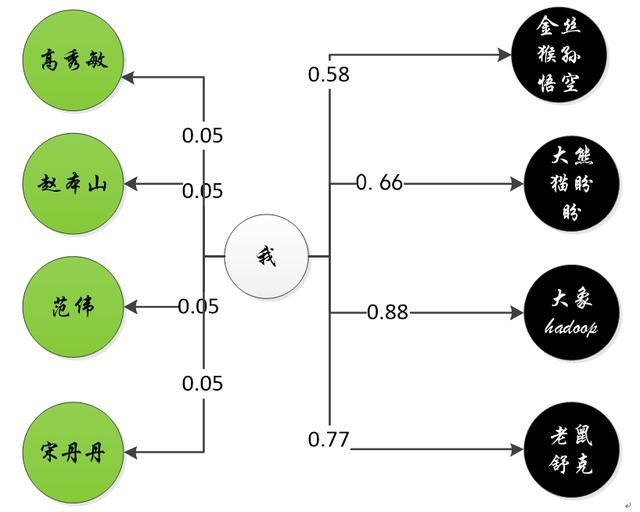
图1-2 4NN分类器
问题来了,前面这些相似度都是捏造的,实际生产中我们应该如何计算距离呢?
1.4距离的计算
1.4.1特征工程
计算相似度,我们需要解决两个问题:(1)构造特征;(2)制定距离计算方式。
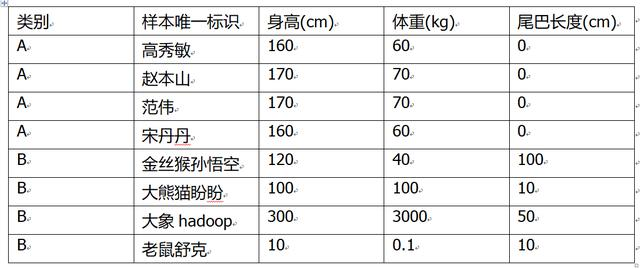
构造特征是一项高难度的任务,这里简单做。我们选择生物的(身高,体重,尾巴长度)这3个易测量的尺寸或者重量,作为特征。具体(伪造)取值情况如表1-1。
表1-1 训练集特征取值情况
1.4.2欧氏距离
我们用欧氏距离来的来计算样本i和样本j之间的距离:
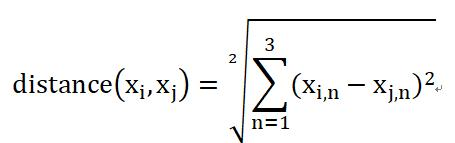
其中x_i和x_j是两个样本的特征向量。比如我的特征向量取值为(175,70,0),和赵本山的距离是:
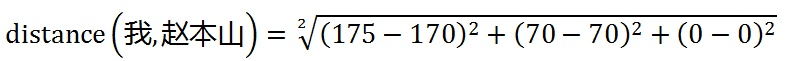
那么,我与训练集的A类样本的相似度就是:

注意,我们在表述的时候经常出现"N位一体"的情况,容易造成混淆。比如上面这个等式中“distance(我,赵本山)”中的“我”实际上是我的特征向量取值。
这种看起来节省文字的表述方式对码字的人来说比较简便,虽然有语病的嫌疑,但是比较普遍——只好适应了,学习的时候脑子里自动建立连接即可。
1.5可以升级的地方
1.4提出的分类器可以升级的地方很多:
(1)特征工程,我们可以用PCA之类的方法搞一个降维、把特征里重要的信息突出一下,这样分类器的效果会提升一些;
(2)选取合适的距离计算方式,特征目前是有量纲的,要特别注意特征的绝对值大小对欧氏距离影响很大,可以尝试一下余弦距离之类的;
(3)资源允许的情况下再加一点训练样本。
2 kNN的python实现
import numpy as np
#一个最简单的KNN
class KNN():
def __init__(self):
self.model = {}#存储各个类别的训练样本的特征,key为类别标签,value是一个list,元素为样本的特征向量
self.training_sample_num = {}#存储训练数据中,各个类别的数量
#训练模型,输入是标签列表,和对应的输入数据列表
def fit(self, X, Y):
for i in range(len(Y)):
#将训练数据按照类别分组
if Y[i] in self.model:
self.model[Y[i]].append(X[i])
else:
self.model[Y[i]] = [X[i]]
#各个类别的样本总数
self.training_sample_num[Y[i]] = self.training_sample_num.get(Y[i], 0) + 1
#预测/判断一个样本的类别。这里模仿sklearn的风格,允许输入单个样本,也允许输入多个样本
def predict(self, X):
result = None
if type(X[0])==list:
for x in X:
result.append(self.predict_one(x))
else:
result = self.predict_one(X)
return result
#判断单个样本的类别
def predict_one(self, x):
label = None#类别标签
min_d = None#目前为止,待分类样本与各类代表性样本的最小平均距离
for class_label in self.model:#遍历每个类别的代表性样本
sum_d = 0#待分类样本与本类别的代表性样本的距离之和
for sample in self.model[class_label]:#遍历这个类别下所有的代表性样本
sum_d += self.distance(x, sample)#累计
mean_d = sum_d/self.training_sample_num[class_label]#待分类样本与本类别的代表性样本的平均距离
if min_d==None or mean_d<=min_d:#如果遍历到第一个类别,或者待分类样本与当前类别的平均距离比之前的更低,更新类标签与最小距离
label = class_label
min_d = mean_d
return label
#计算两个样本之间的距离
def distance(self, x1, x2, type="eu"):
d= None
if type=="eu": d = np.sum((x1-x2)**2)#欧氏距离
return d
#评估模型效果
def eveluate(self, X, Y):
pass
#制造训练数据
def generate_training_data(self):
data_str = """类别 样本唯一标识 身高(cm) 体重(kg) 尾巴长度(cm)
A 高秀敏 160 60 0
A 赵本山 170 70 0
A 范伟 170 70 0
A 宋丹丹 160 60 0
B 孙悟空 120 40 100
B 大熊猫 100 100 10
B 大象 300 3000 50
B 老鼠 10 0.1 10"""
print(data_str)
data_list = data_str.split('\n')
X = []
Y = []
for line in data_list[1:]:
data = line.split(" ")
Y.append(data[0])
X.append(list(map(lambda x: float(x), data[2:])))
return X, Y
if __name__ == '__main__':
M = KNN()
train_X, train_Y = M.generate_training_data()
print(train_X)
M.fit(train_X, train_Y)
xiao_li_zi = np.array([175,75,0])
res = M.predict(xiao_li_zi)
print(res)3 结束语
KNN是我们学数据挖掘或者机器学习时,最早接触的分类算法。比起SVM之类的算法,KNN显得有些简陋,不过如果通过数据探查和分析,如果可以确定样本非常容易分类,使用简单的算法还是挺节省资源的。
KNN算法在实际使用之外,还有教学价值。KNN现在的实用性可能不是特别高,但是由于符合人类思维习惯、比较直观,而且容易实现,是数据科学入门必学算法。
另外,学习聚类算法,比较顺畅的学习路径就是先学习KNN,然后学习kmeans,然后看其他的聚类算法。
原文链接: zhuanlan.zhihu.com/p/76423064 文源网络,仅供学习之用,侵删。
在学习Python的道路上肯定会遇见困难,别慌,我这里有一套学习资料,包含40+本电子书,800+个教学视频,涉及Python基础、爬虫、框架、数据分析、机器学习等,不怕你学不会! shimo.im/docs/JWCghr… 《Python学习资料》
关注公众号【Python圈子】,优质文章每日送达。
