树
树结构在客观世界中的应用,例如族谱,公司架构等
只有根结点的树

一般树
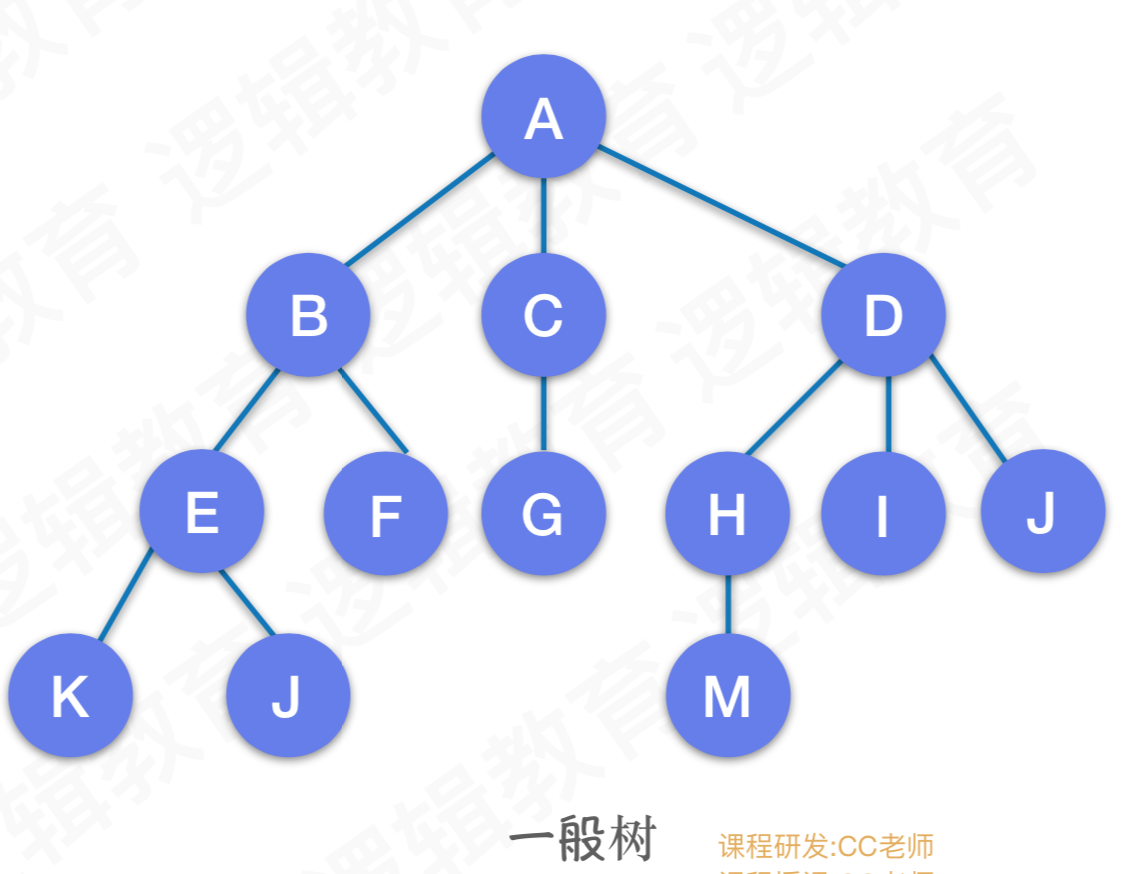
树结构中的高度、深度、层数
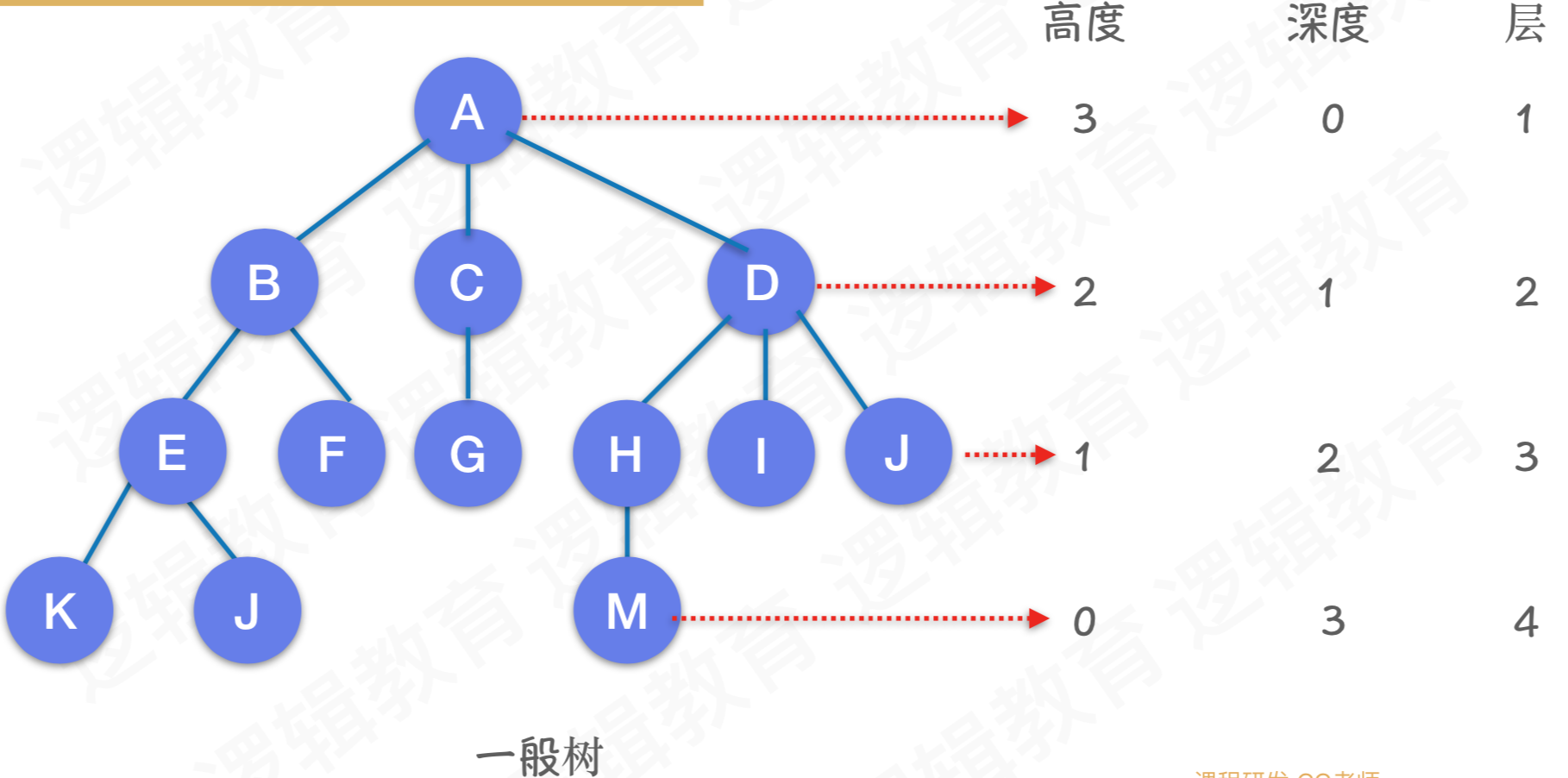
- 高度:叶结点到根结点的最长的边数
- 深度:根结点到叶结点的最长的边数
- 层数:从根开始定义,根为第一层,根的孩子为第二层...
- 度:某个节点的度,就是该节点拥有子节点的数量。上图,节点[A]的度=2, 节点[B]的度=2,节点[D]的度是2、节点[K]到节点[G]的度为0.
- 叶结点:度为0的结点称为叶结点或终端结点
- 结点间的关系:
- 结点的子树的根,称为该结点的孩子结点,该结点也是孩子结点的双亲结点;
- 同一双亲结点下的孩子结点为兄弟结点
- 该结点下所有子树的任一结点为该结点的子孙结点
- 结点的次序:从左向右
我们从上图可以发现
-
在第i层上,有2^i-1个节点
-
最大深度为k时,整个二叉树最多有 2k-1 个节点
-
终端节点数 = 度为2的节点数+1;(终端节点就是叶子节点,度为0的节点)
-
有n个节点完全二叉树,深度 = log_2n+ 1
-
有n个节点的完全二叉树,从根节点开始标号,标号i从1开始,如上面的完全二叉树,那么
- i>1,i节点的双亲节点为i/2;
- 如果i=1,那么序号为i的结点为根节点,无双亲结点
- 如果2i<=n,那么序号为i的结点的左孩子结点序号为2i
- 如果2i>n,那么序号为i的结点无左孩子
- 如果2i+1<=n,那么序号为i的结点右孩子序号为2i+1
- 如果2i+1>n,那么序号为i的结点无右孩子
二叉树
每个节点有且最多只有两个节点的树叫做二叉树
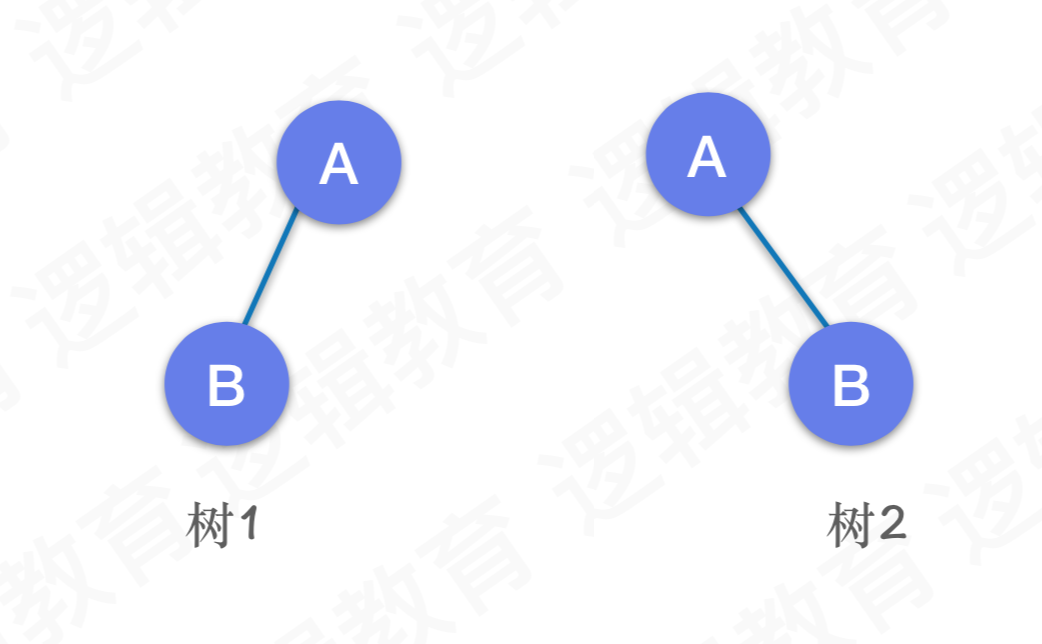
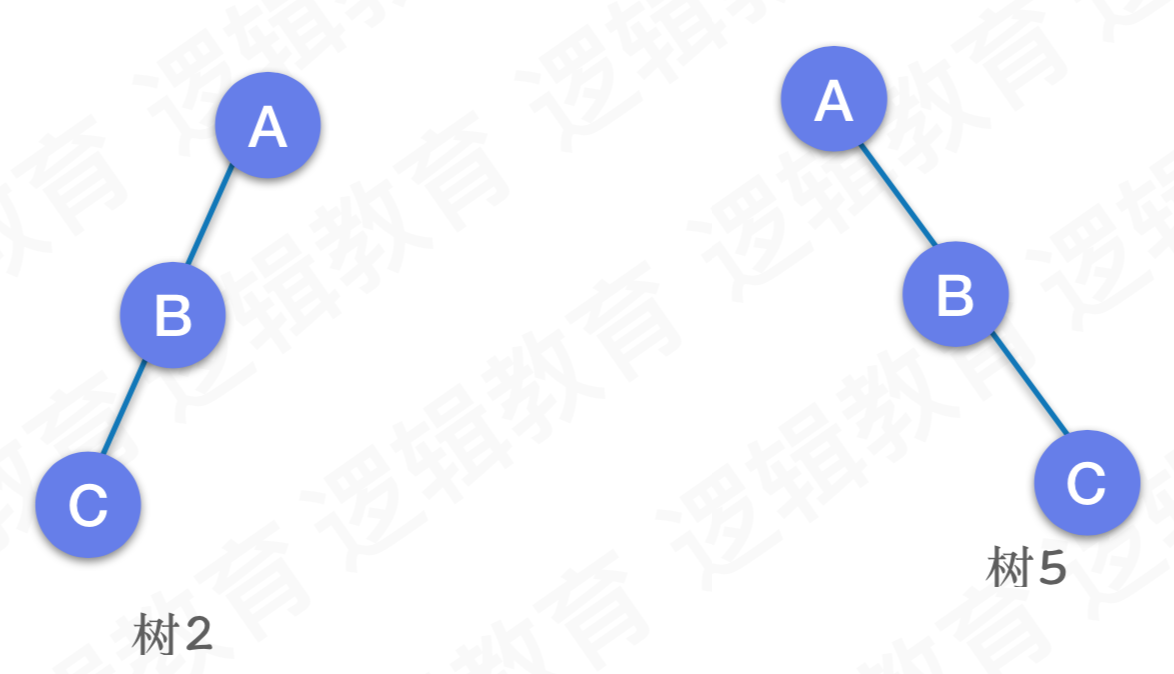
特殊二叉树-斜树
所有结点都只有左子树或者右子树,那么分别称之为左斜树/右斜树
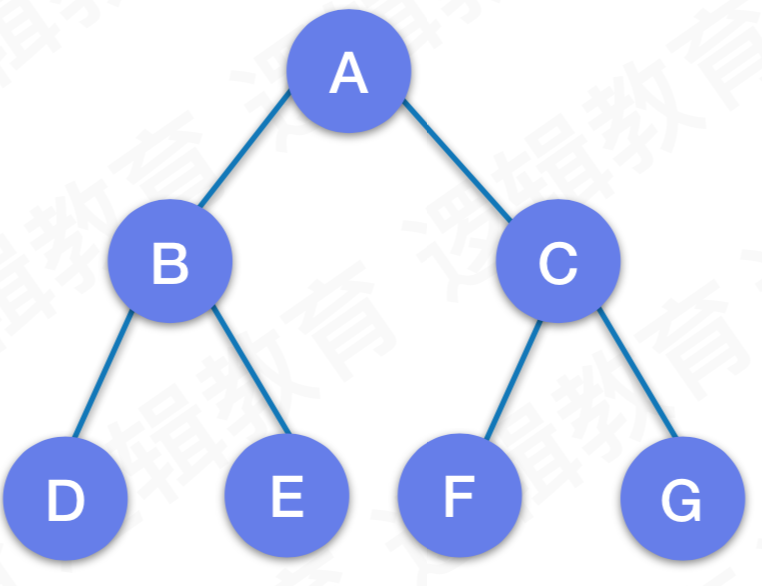
特殊二叉树-满二叉树
满二叉树:所有的结点都有两个子树,并且叶子结点都在同一层。(整体看来是左右对称的)
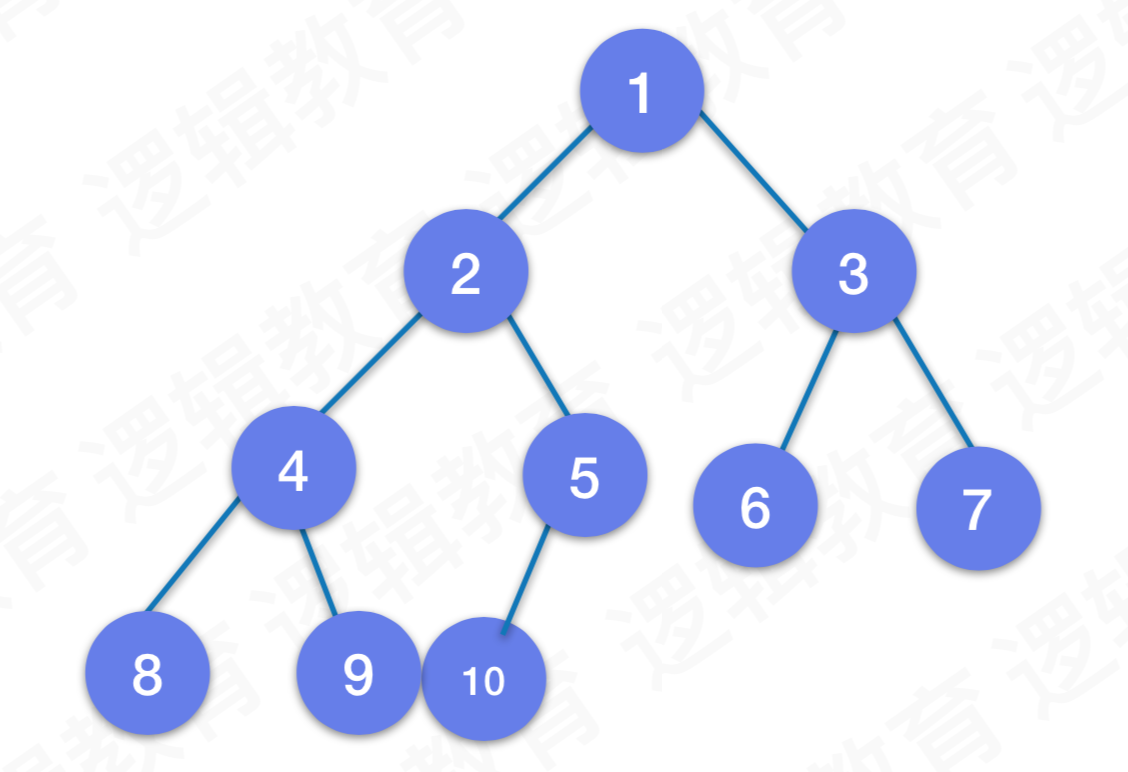
特殊二叉树-完全二叉树
完全二叉树的所有结点与同样深度的满二叉树,按照层序编号相同的结点,是一一对应的。
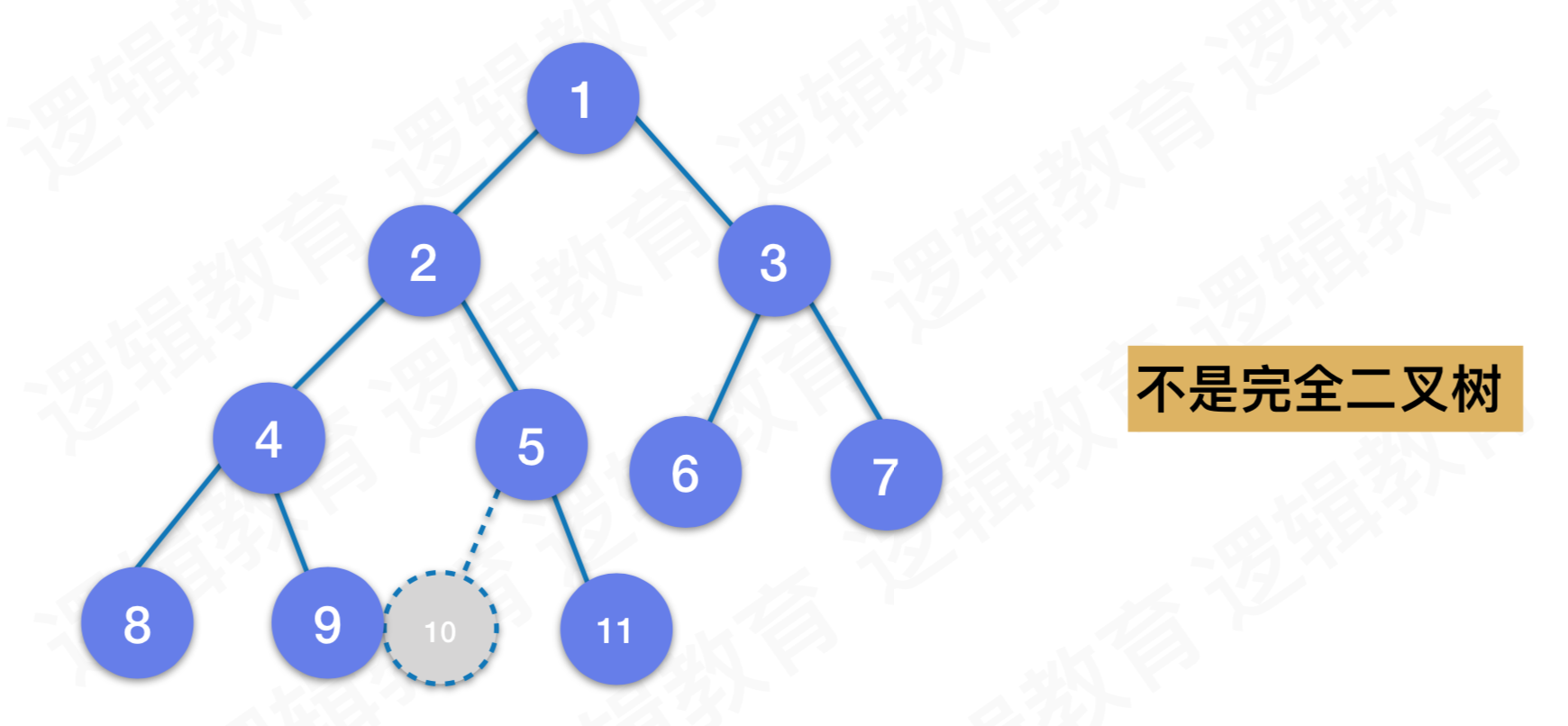
完全二叉树的判断
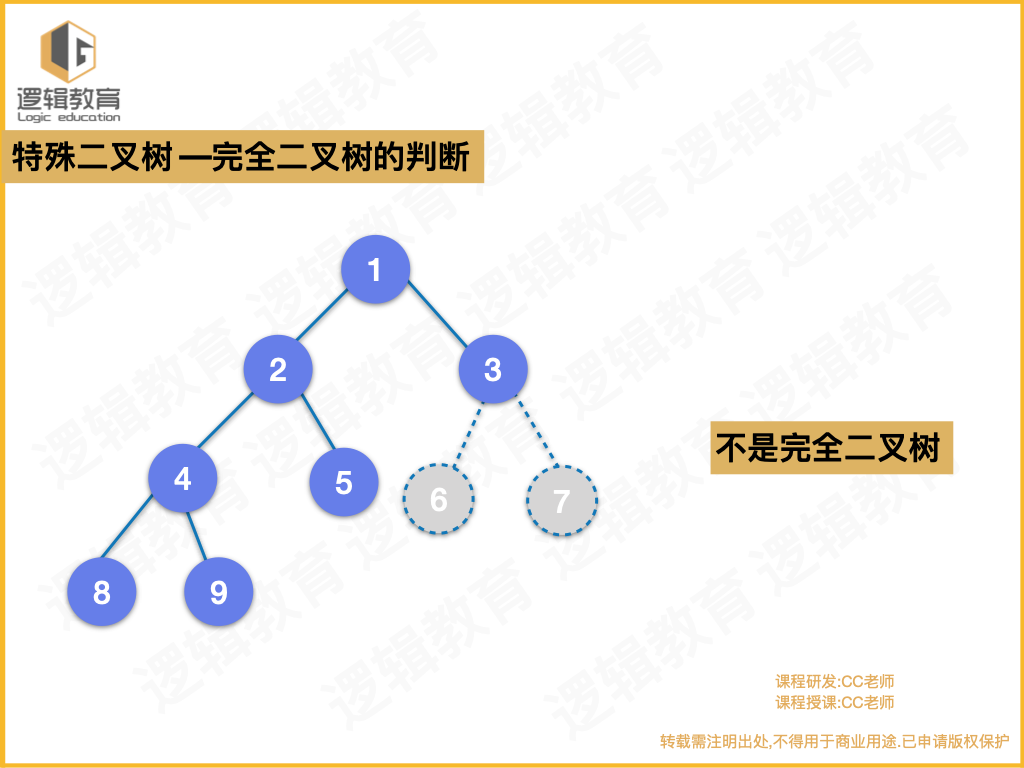
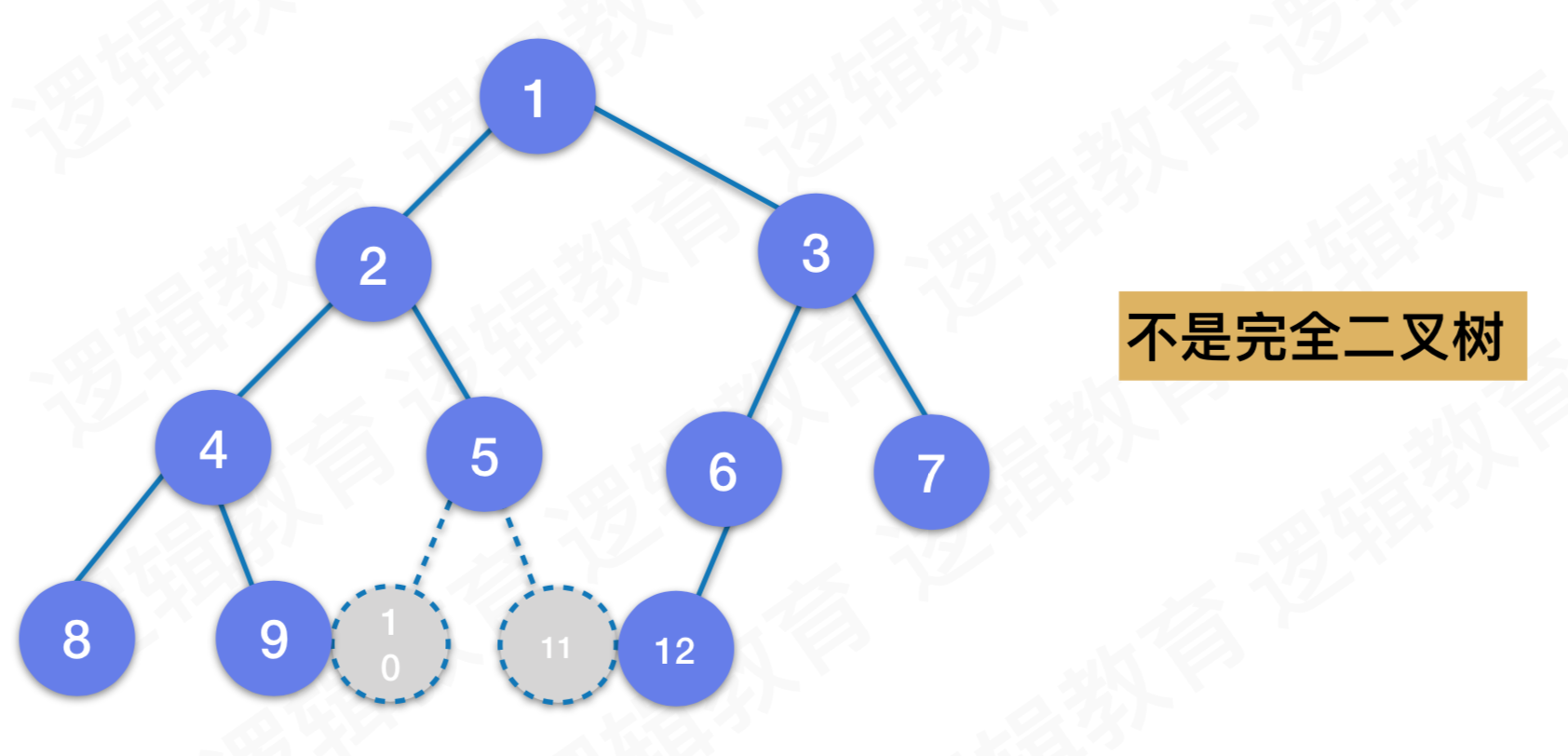
二叉树的遍历 - 前序遍历
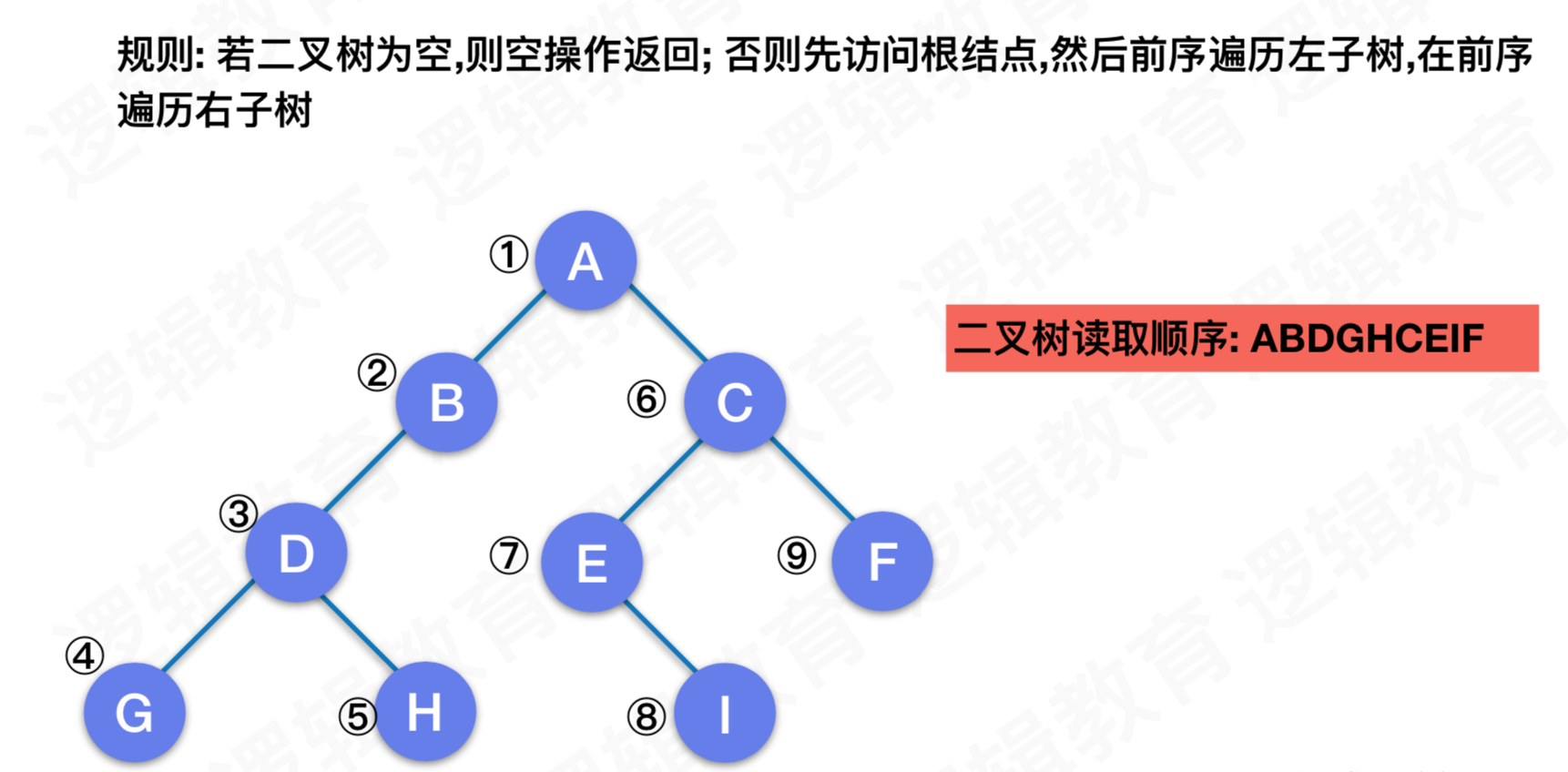
二叉树的遍历 - 中序遍历
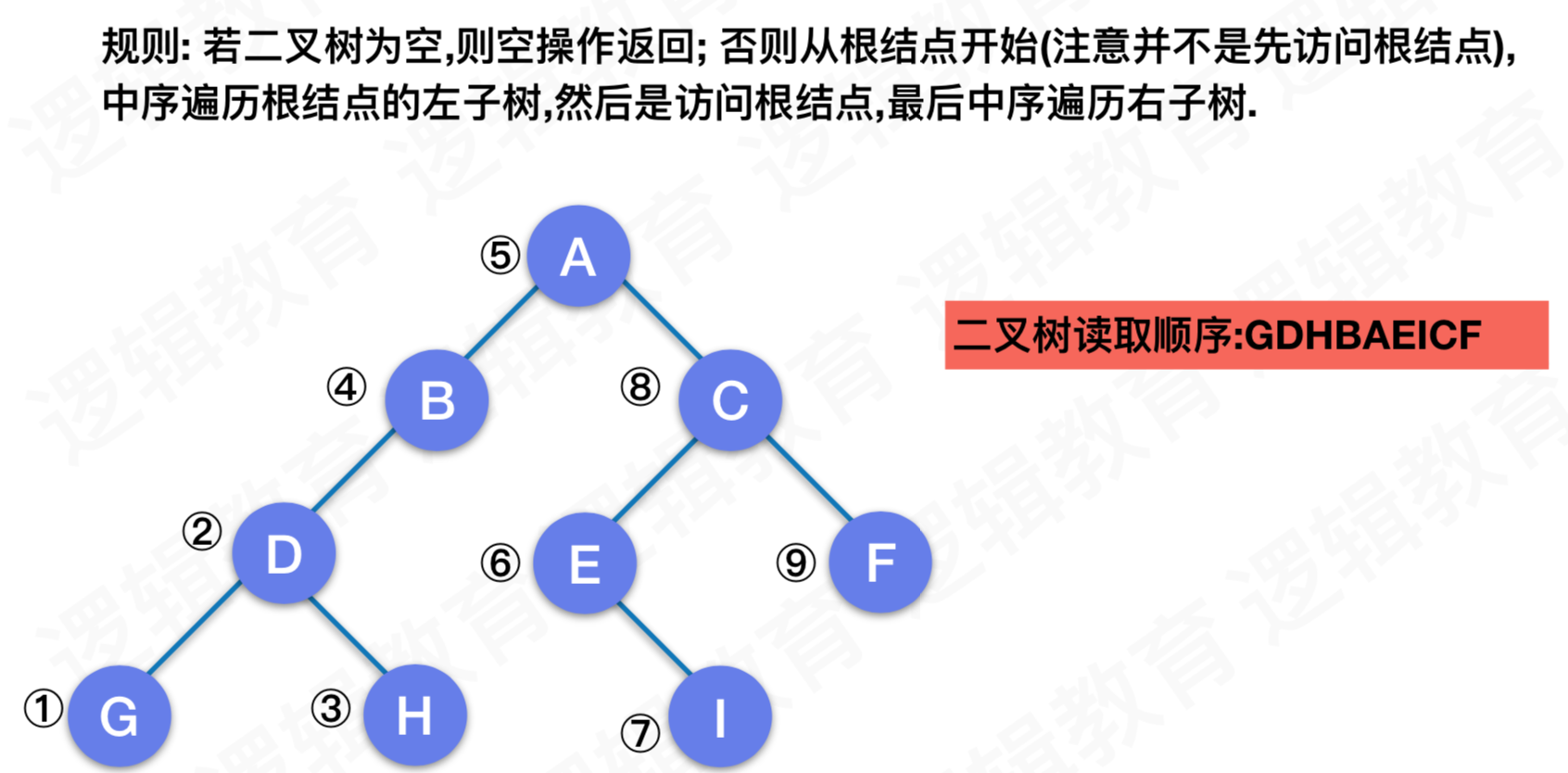
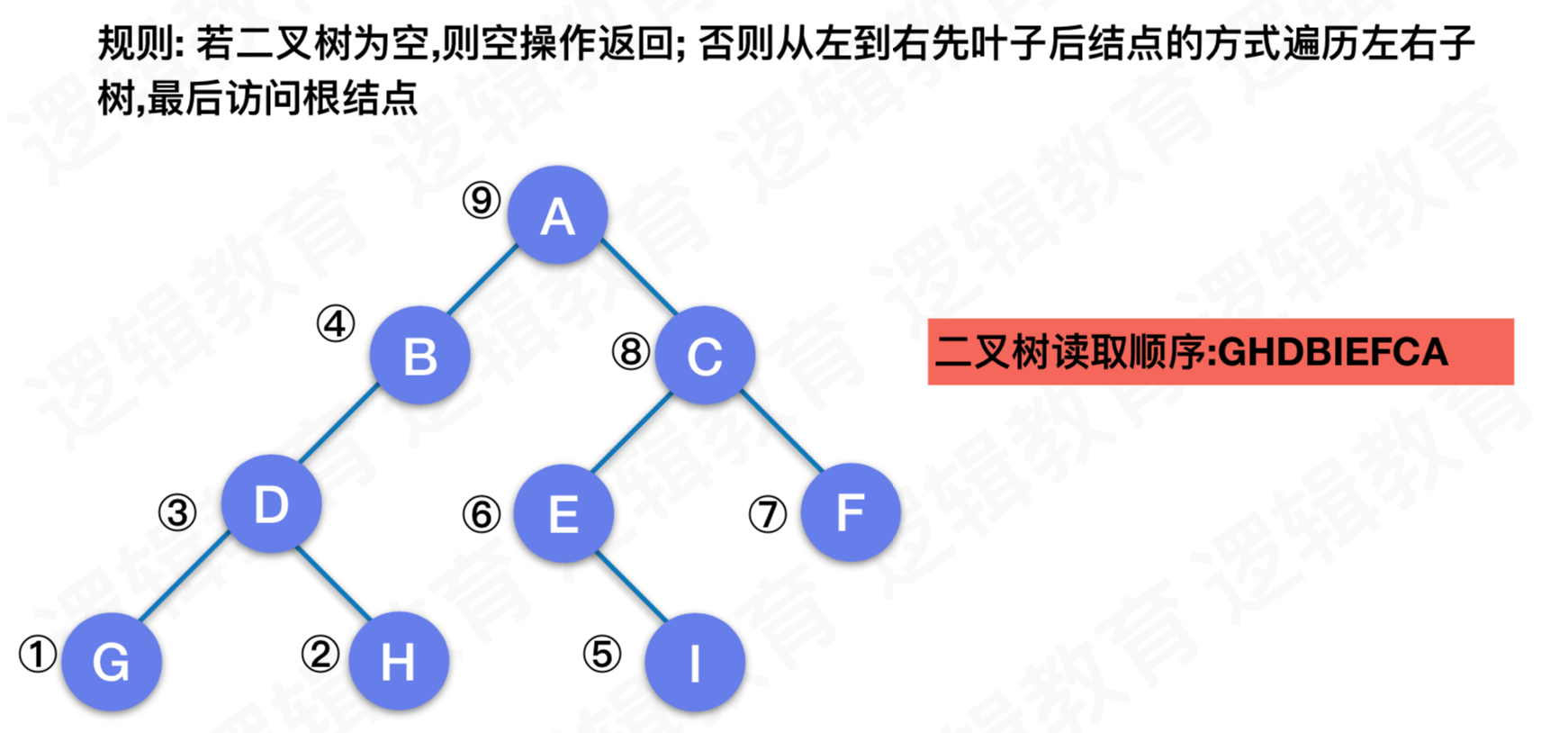
二叉树的遍历 - 后序遍历
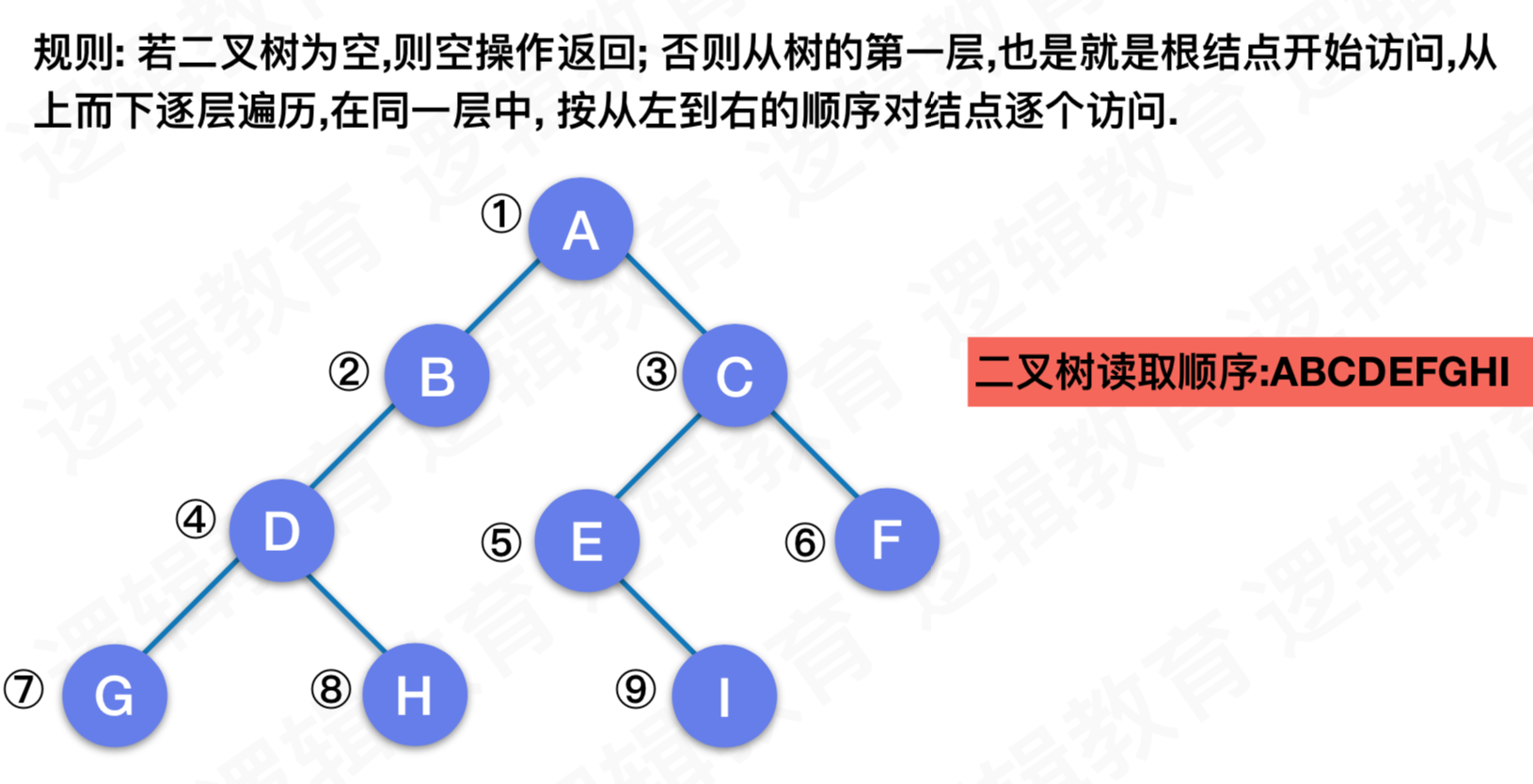
二叉树的遍历 - 层序遍历