一、堆的定义
堆是计算机科学中一类特殊的数据结构的名称,堆通常是一个可以被看做一颗完全二叉树(完全二叉树指的是除了最底层,每一层都是满的)的数组对象,堆总是满足以下性质:
1.堆中某个节点的值总是不大于或不小于其父节点的值;
2.堆总是一颗完全二叉树
将根节点最大的堆叫做最大堆或者大根堆,根节点最小的堆叫做最小堆或者小根堆,常见的堆有二叉堆、斐波那契堆等,堆是非线性数据结构,相当于一维数组,有两个直接后继
二、堆的数据结构图
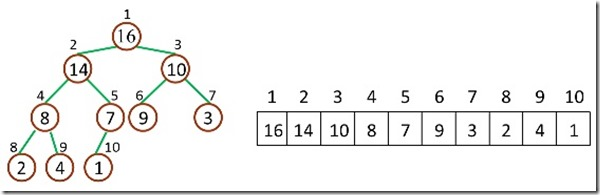
例如:上图给定的一个js 数组完全可以用左侧的二叉树来表示
但是数组都是以 0为基数,所以对应关系如下:
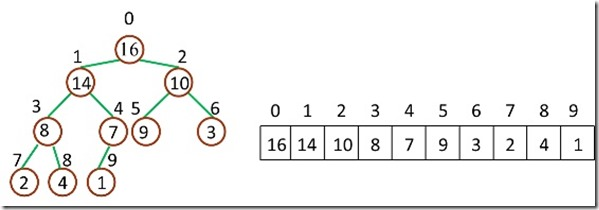
节点计算方式如下:
-
Parent(i) = floor((i-1)/2), i 的父节点下标
-
Left(i) = 2i +1, i 的左子节点下标
-
Right(i) = 2(i+1), i 的右子节点下标
三、堆的操作
1.堆排序
操作思路:
1.将需要排序的数组构造成一个最大堆,此时,整个数组的最大值就是堆结构的顶端
2.将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序的数组个数n-1
3.将剩余的n-1个数再构造成最大堆,再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序数组
1.1构造堆
将无序数组构造成堆(升序用最大堆,降序用最小堆)
如下数组:
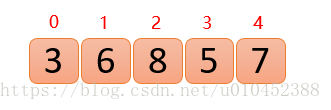
操作思路:第一次吧保证0~0位置最大堆结构,第二次保证0~1位置最大堆结构,第三次保证0~2位置最大堆结构...直到保证0~1位置最大堆结构(每次新插入的数据都与其父节点进行比较,如果插入的数比父节点大,则与父节点交换,否则一直向上交换,直到小于或者等于父节点,或者来到了顶端)
插入6的时候,6大于他的父节点3,即arr(1) > arr(0),则交换,此时,保证了0~1位置是最大堆,如图所示:
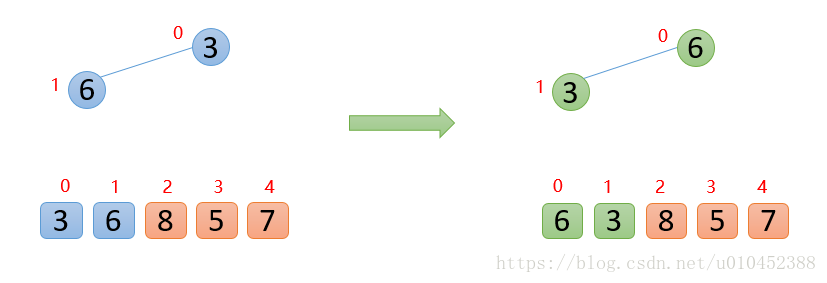
插入8的时候,8大于其父节点6,即arr(2) >arr(0),则交换,此时,保证了0~2位置是最大堆结构,如图:
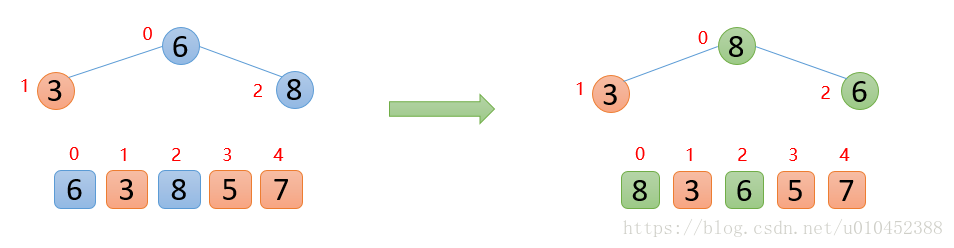
插入5的时候,5大于其父节点3,则交换之后,5又发现比8小,所以不交换;此时,保证了0~3位置最大堆结构,如下图:
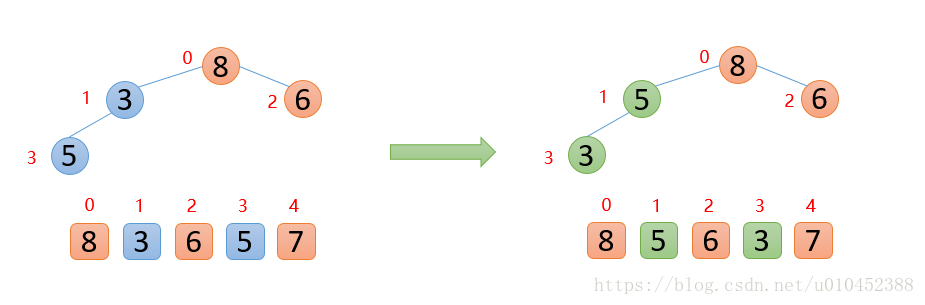
插入7的时候,7大于其父节点5,则交换,交换之后,7又发信比8小,所以不交换,此时整个数组已经是最大堆结构
1.2固定最大值再构建堆
现在我们已经有一个最大堆,下面将顶端的数与最后一位数交换, 然后将剩余的数在构造成一个最大堆
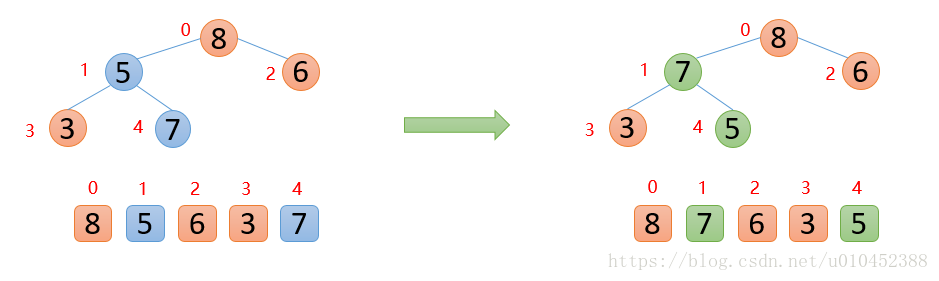
此时最大数8已经来到末尾,则固定不动,后面只需要对顶端的数据进行操作即可,拿顶端的数与其左右子节点较大的数进行比较,如果顶端的数大于其左右子节点较大的数,则停止,如果顶端的数小于其左右子节点较大的数,则交换,然后继续与下面 的子节点进行比较
如下图,5的作用子节点中,左子节点比右子节点大,则5与7进行比较,发现5 < 7,则交换,交换后,发现5已经大于他的子节点,说明剩余的数已经构成最大堆,后面就是重复固定最大堆,然后构造最大堆

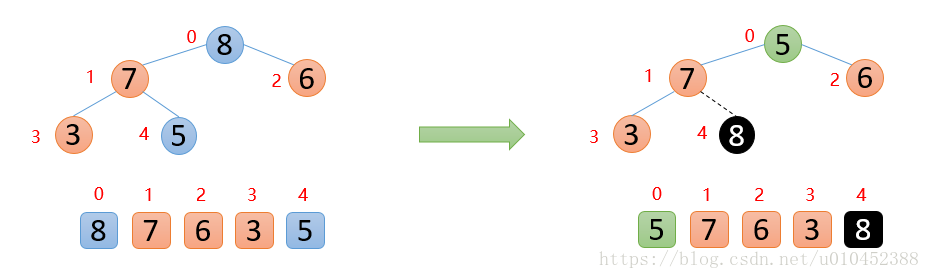
如下图:顶端7与末尾数3进行交换,固定好7
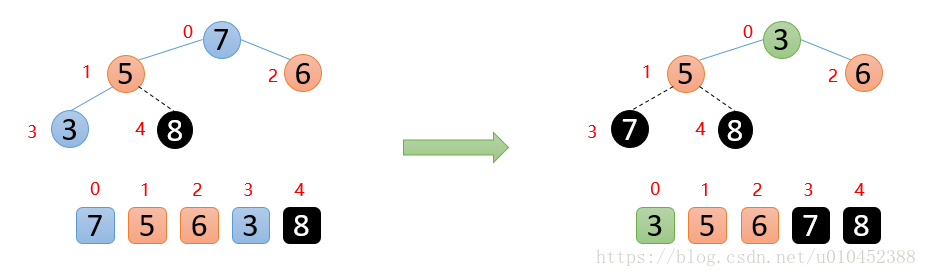
剩余的数开始构造最大堆,然后顶端数与末尾数交换,固定最大值在构造最大堆,重复执行上面的操作,最终会得到有序数组
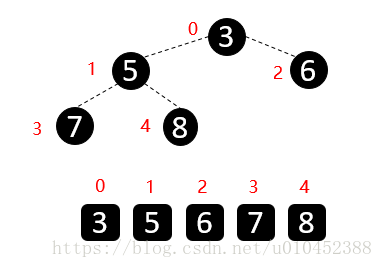
1.3总结
堆排序流程:
1.将无序数组构造成一个最大堆
2.固定一个值,将剩余的数重新构造一个最大堆,重复这样的过程
1.4实现代码
/**
* 从 index 开始检查并保持最大堆性质
*
* @array
*
* @index 检查的起始下标
*
* @heapSize 堆大小
*
**/
function maxHeapify(array, index, heapSize) {
var iMax = index,
iLeft = 2 * index + 1,
iRight = 2 * (index + 1);
if (iLeft < heapSize && array[index] < array[iLeft]) {
iMax = iLeft;
}
if (iRight < heapSize && array[iMax] < array[iRight]) {
iMax = iRight;
}
if (iMax != index) {
swap(array, iMax, index);
maxHeapify(array, iMax, heapSize); // 递归调整
}
}
function swap(array, i, j) {
var temp = array[i];
array[i] = array[j];
array[j] = temp;
}
/*创建最大堆*/
function buildMaxHeap(array, heapSize) {
var i,
iParent = Math.floor((heapSize - 1) / 2);
for (i = iParent; i >= 0; i--) {
maxHeapify(array, i, heapSize);
}
}
/*堆排序*/
function heapSort(array, heapSize) {
buildMaxHeap(array, heapSize);
for (let i = heapSize - 1; i > 0; i--) {
swap(array, 0, i);
maxHeapify(array, 0, i);
}
}
1.5时间复杂度与排序稳定性
1.5.1 堆调整时间复杂度
从堆调整的代码可以看到是当前节点与其子节点比较两次,交换一次。父节点与哪一个子节点进行交换,就对该子节点递归进行操作,设对调整的时间复杂度为T(k)(k为该层节点到叶节点的距离),那么有:
-
T(k) = T(k -1) +3, k∈[2,h]
-
T(1) = 3
迭代法计算结果为:
T(h) = 3h = 3floor(log n)
所以堆调整的时间负责度是O(log n)
1.5.2 建堆的时间复杂度
n个节点的堆,树高度是 h = floor*(log n )
对深度位于h-1层的节点,比较2次,交换1次,这一层最多有2^(h-1)个节点,总共操作次数最多为3(12^(h-1));对深度为h-2层的节点,总共有2^(h-2)个。每个节点最多比较4次,交换2次,所以操作次数最多为3(22^(h-2))……,
一次类推,从最后一个父节点到跟节点进行堆调整的总共操作次数为:
s=3*[2^(h-1) + 2*2^(h-2) + 3*2^(h-3) + … + h*2^0] a
2s=3*[2^h + 2*2^(h-1) + 3*2(h-2) + … + h*2^1] b
b-a,得到一个等比数列,根据等比数列求和公式
s = 2s - s = 3*[2^h + 2^(h-1) + 2^(h-2) + … + 2 - h]=3*[2^(h+1)- 2 - h]≈3*n
所以建堆的时间复杂度是O(n)
1.5.3堆排序时间复杂度
堆排序的时间等于建堆和进行堆调整的时间之和,所以堆排序的时间复杂度是O(nlog n + n) =O(nlog n)
1.5.4稳定性
堆排序是不稳定的算法,它不满足稳定算法的定义,它在交换数据的时候,是比较父节点和子节点之间的数据,所以,即便是存在两个数值相等的兄弟节点,它们的相对顺序在排序也可能发生变化