参考链接：KMP算法

KMP概念

KMP 算法也是比较著名的模式匹配算法. 是由D.E.Knuth,J.H.Morrs 和VR.Pratt. 发表的一个模式匹配算法，可以大大避免重复遍历的情况;

KMP原理探索

正常我们字符串匹配方式，假如用暴力法的话：假设, 主串S = “abcdefgab” ; 模式串 T = “abcdex”，第一次匹配情况：

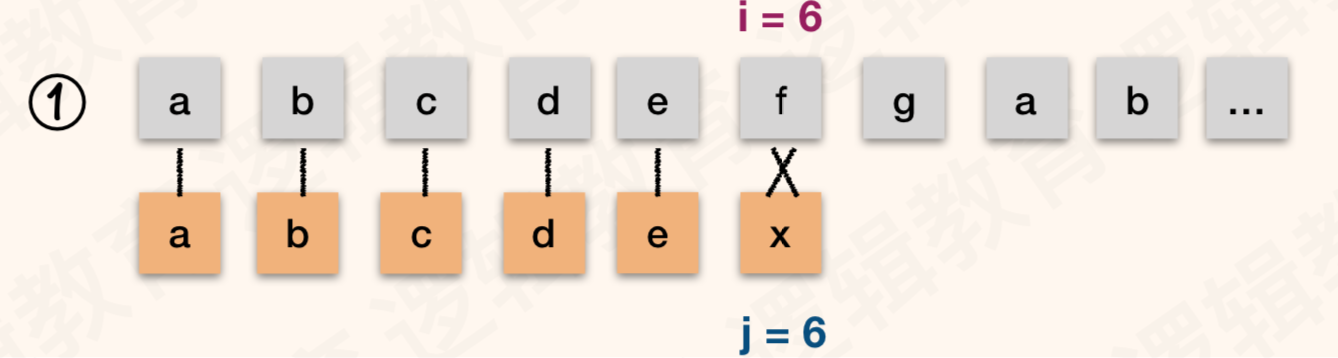
假如匹配不成功的话，我们会将i变成2，j变成1来进行下一次匹配

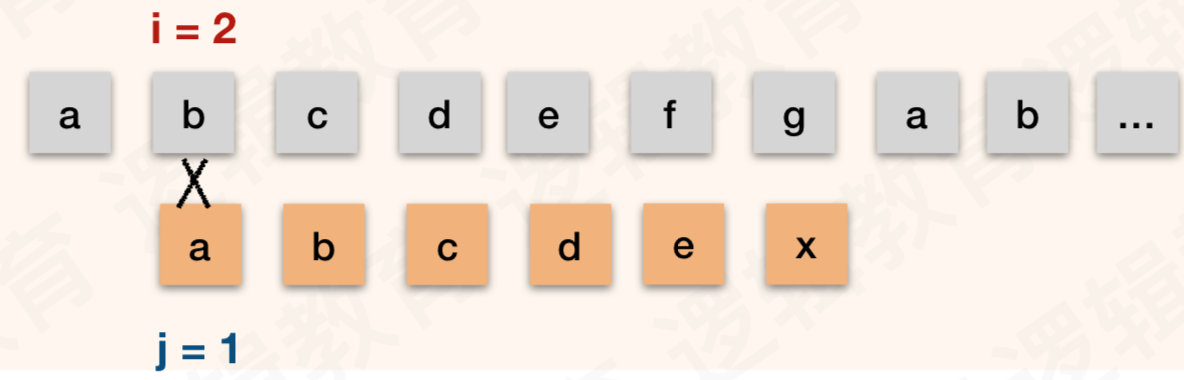
这样依次类推

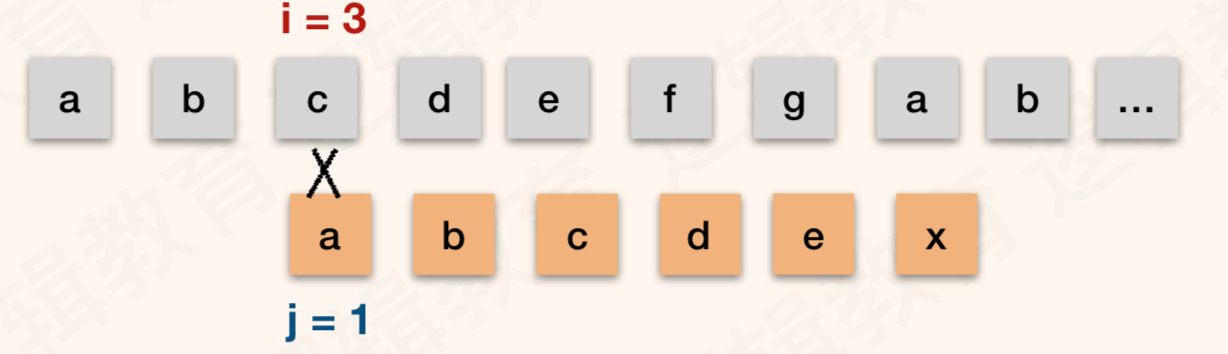
我们会发现，当第六位匹配失败时候，因为模式串的首字母a跟主串的前几位都不同，所以从第二位到第六位的匹配肯定是失败的，所以这些匹配都是多余的

KMP算法的思想就是设法利用这个已知信息，不要把"搜索位置"移回已经比较过的位置，继续把它向后移，这样就提高了效率

推导流程

情况1：

假设, 主串S = “abcdefgab” ; 模式串 T = “abcdex”

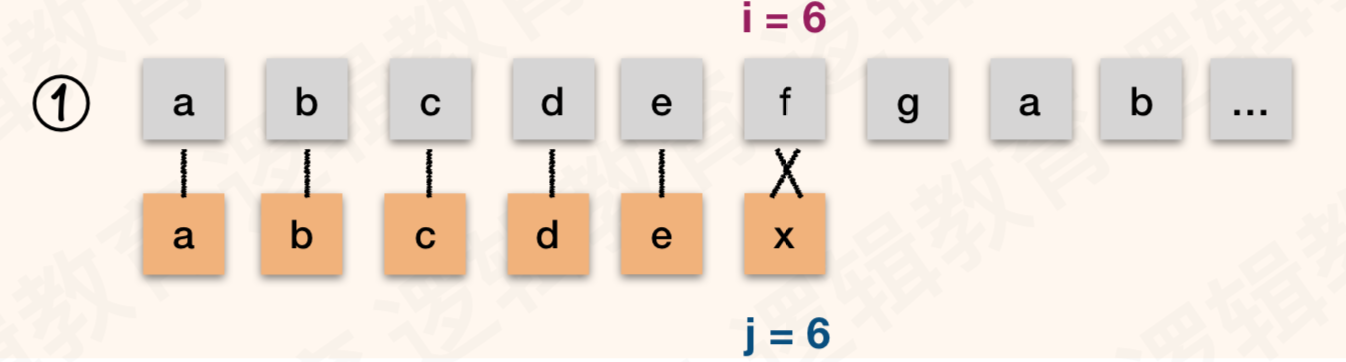
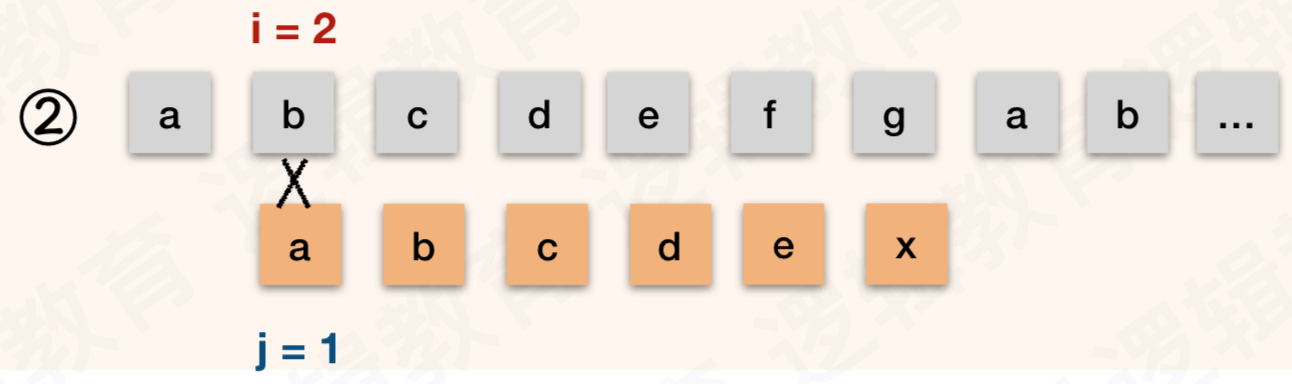
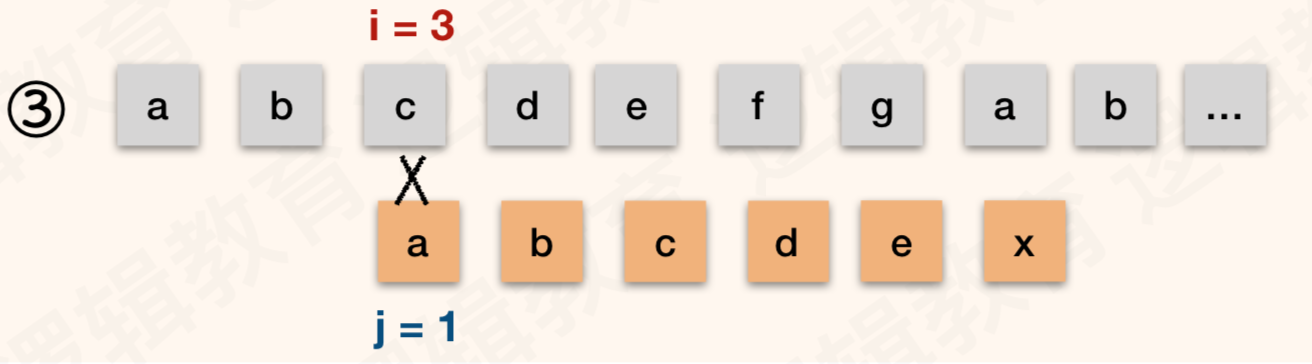
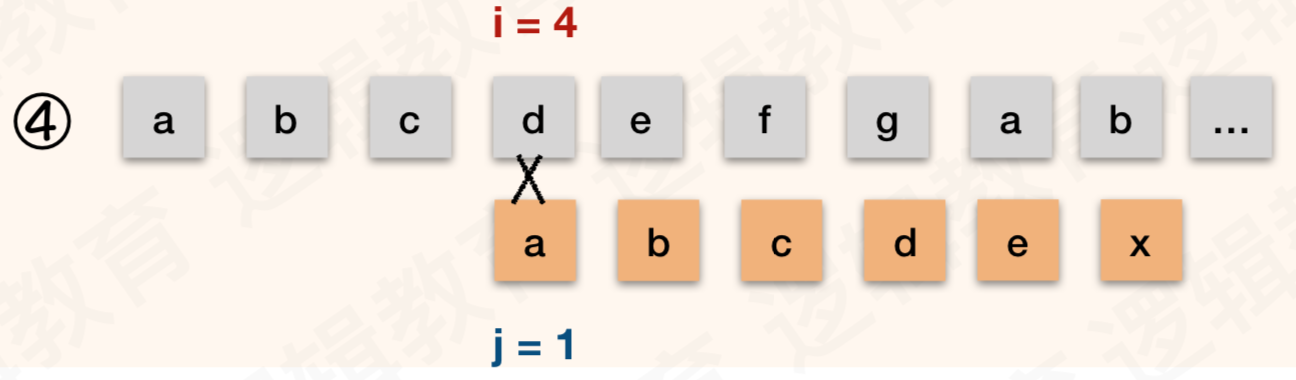
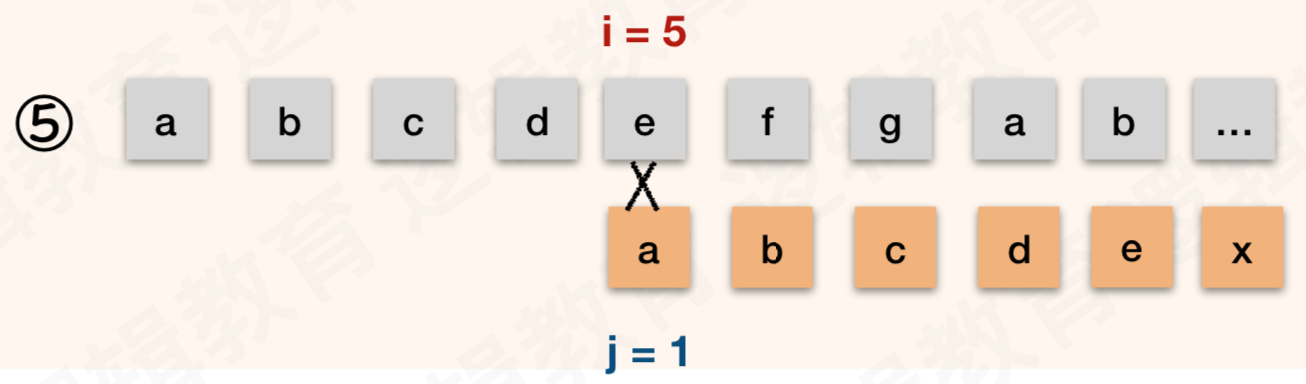
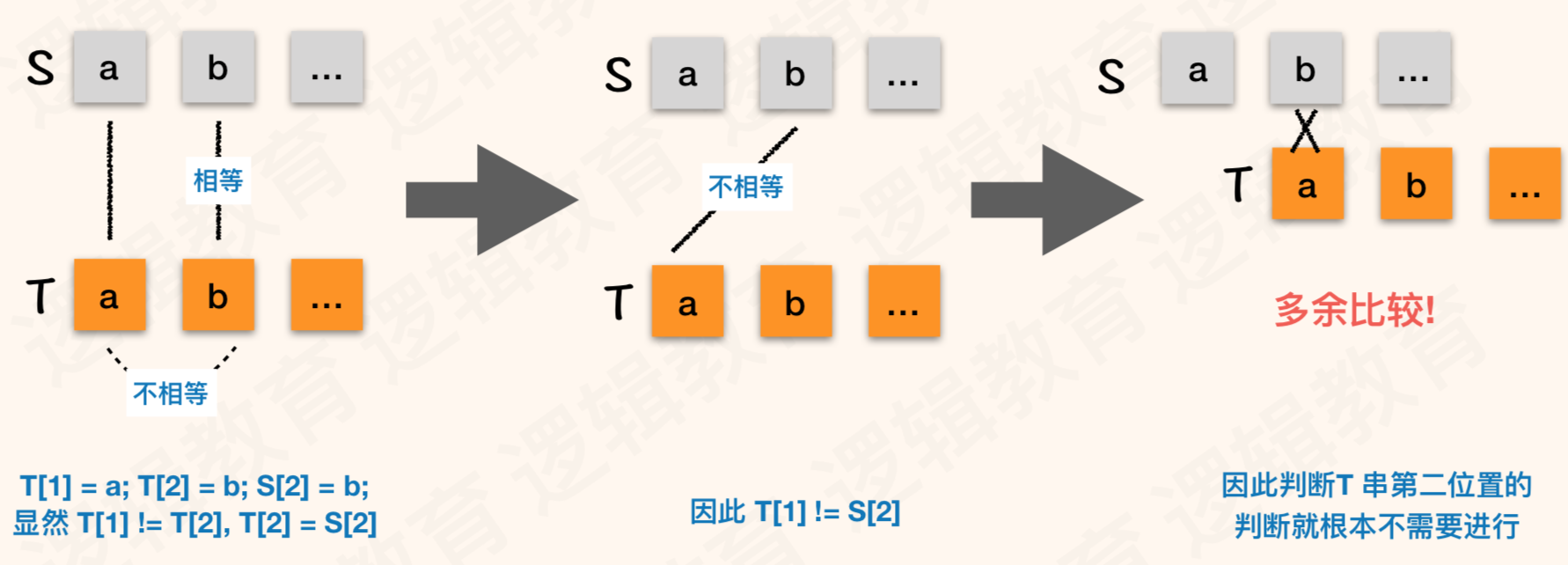
如果我们知道 T 串中的首字母"a" 与 T 中后面的字符均不相等(注意这是前提,如何判断后面会说明);
并且 T 串的第二位的 "b" 与 S 串中的第二位的 "b" 在第①图已经判断相等.
那么就意味着. T串中的首字符 "a" 与 S 串中的第二位 "b" 是不需要判断. 也知道他们不可能相等; 那么图②是可以省略的!
同样的道理,在我们知道T串中首字母 "a" 与 T 中的后面字符均不相等的前提下, T 串的 "a" 与 S 串中的 "c" "d" "e" 也都可以和在于 ①图之后就确定是不相等的. 所以②③④⑤ 都是没有必要的;

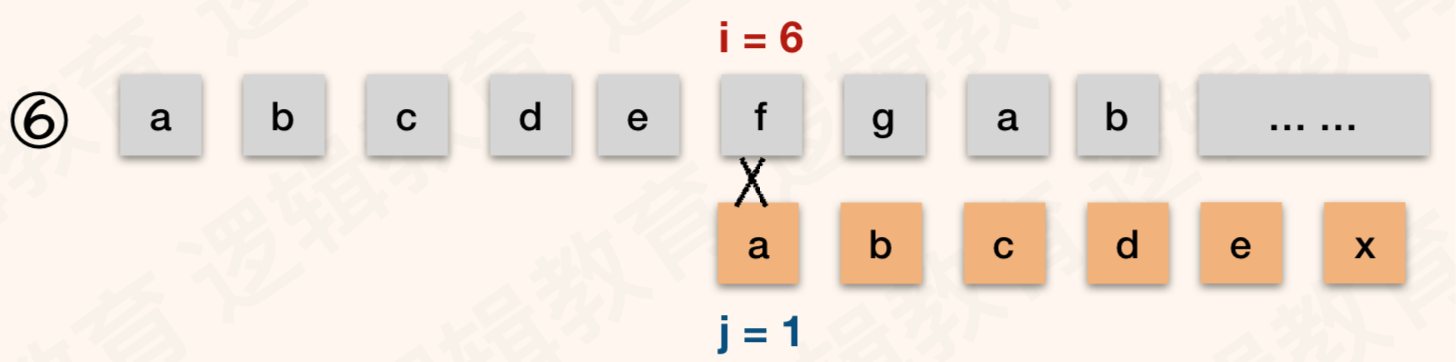
之所以会保留第⑥次判断是因为在①中 T[6] != S[6],尽管我们已经知道T[1] != T[6]. 但是不能断定 T[1] 一定不等于 s[6]. 因此需要保留第⑥步;

情况2 - 如果主串中有和首字符相同的字符

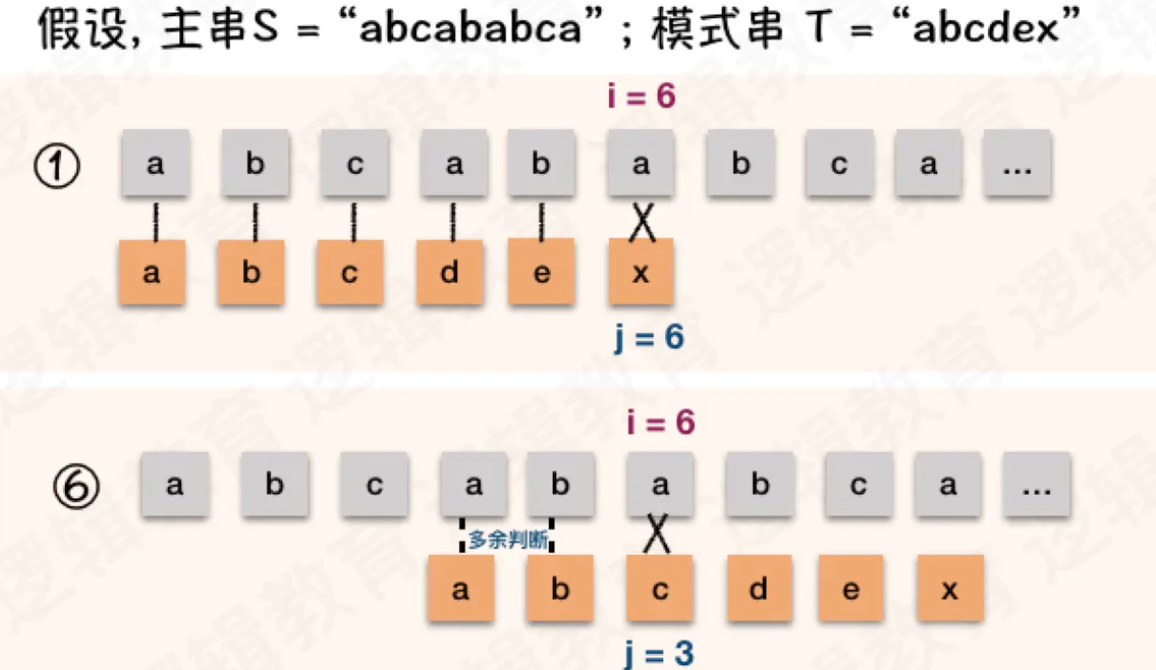
假设, 主串S = “abcdefgab” ; 模式串 T = “abcdex”

对于开始的判断,前 5 个字符完全相等. 第6个字符不相等; 如果下图①.

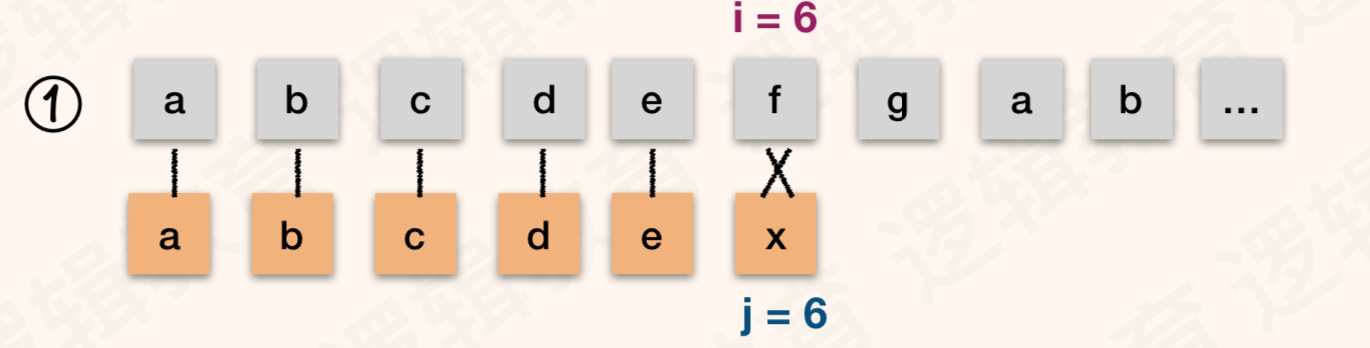
根据刚才的经验,T 的首字符 "a" 与 T的第二位字符 "b" ,第三位字符 "C" 均不相等，所以不需要做判断了.那么步骤②③都是多余的;

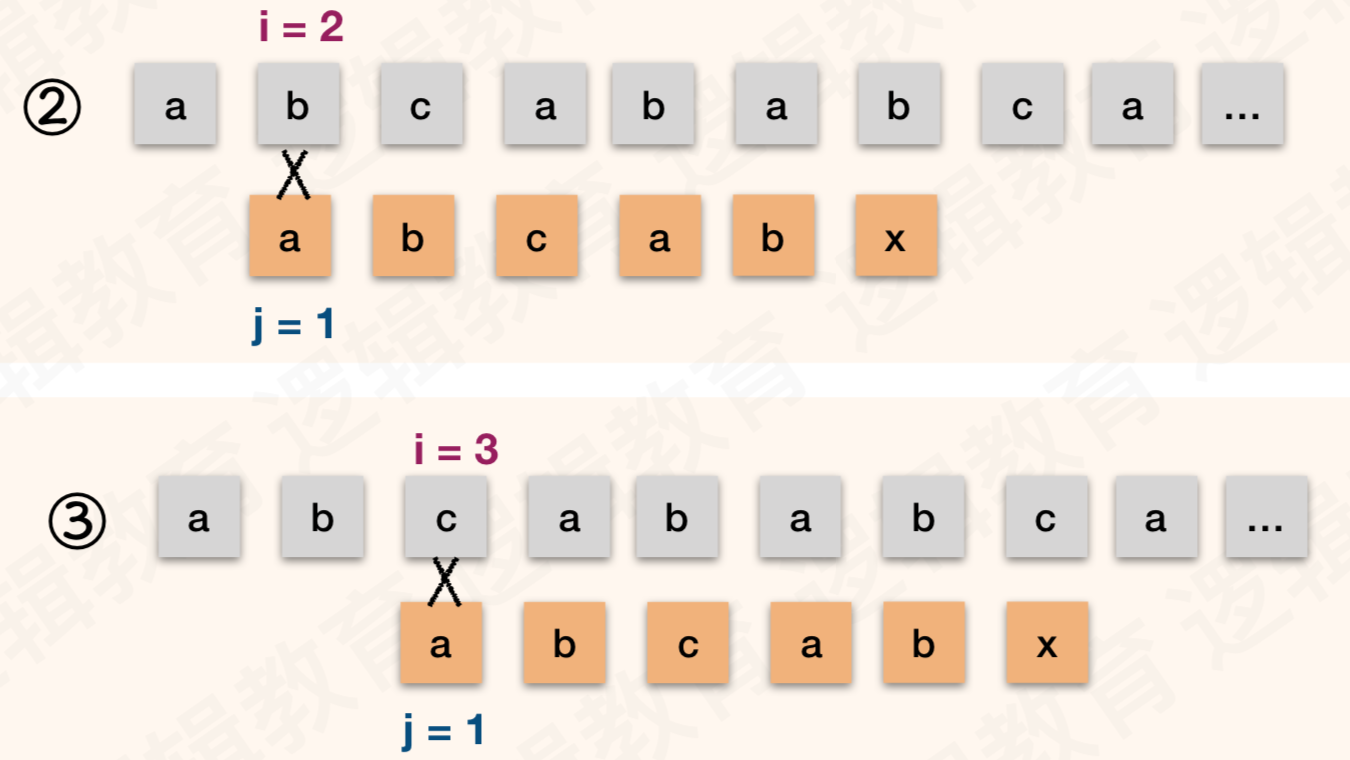
因为 T 的首位"a" 与 T 的第四位的 "a" 相等, 第二位的 "b" 与第五位的 "b" 相等;
而且在第①次比较时, 第四位的 "a" 与第五位的 "b" 已经与主串 S 中的相应位置比较过了.是相等的;
因此可以断定: T 的首字符 "a", 第二字符 "b" 与 S 的第四位字母"a" 和第五位字母"b" 不需要在做比较了. 肯定也是相等的.
所以④⑤的比较也是多余的;

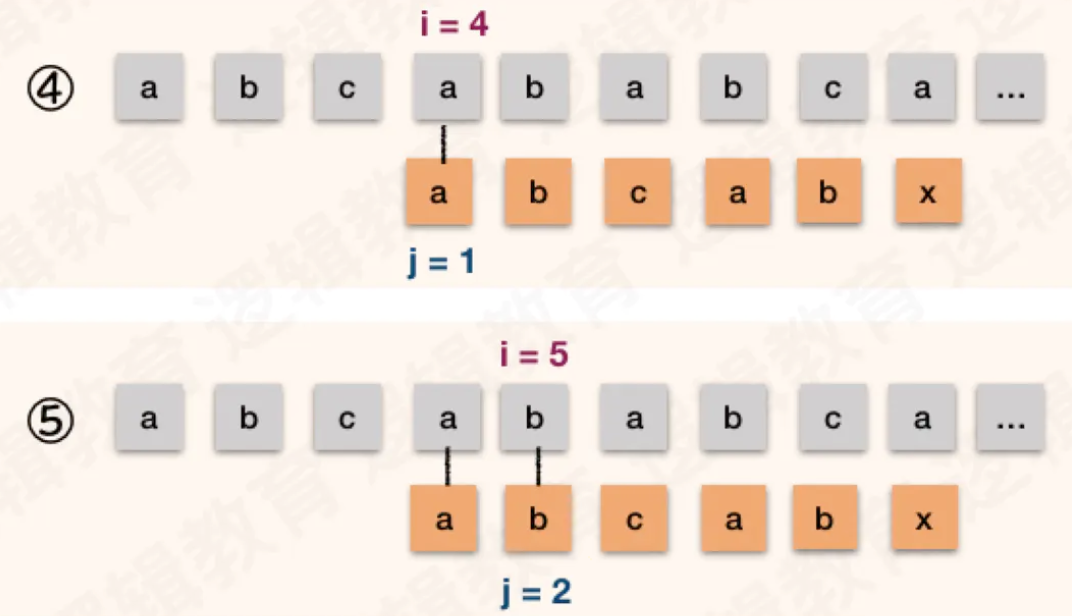
也就是说,对于子串中有与首字符相等的字符,也是可以省略一部分不必要的判断步骤;
如下图所示, 省略了 T 串前两位 "a" 与 "b" 同 S 串中的 4,5 位置字符匹配操作!

对比这2个例子中, 我们会发现 ① 时,我们的 i 值,就是主串当前位置的下是 6 ;
②③④⑤ ,i 的值是 2,3,4,5, 到了 ⑥ 时,i 值又回到了6.
当我们在暴风匹配算法中, 主串的 i 值是不断地回溯来完成的;
而在刚刚的分析中,有很多不必要的回溯;
而KMP 算法就是为了让不必要的回溯发生!
既然 i 值不能回溯, 也不可以变小; 那么考虑的变化就是 j 值;
通过刚刚的分析了解,我们屡次提到了 T 串的首字符与自身后面字符的比较;
发现如果有相等字符, j值的变化就会不相同;
也就是说, j 值的变化其实与主串的关系.
更多取决于T串中的结构是否有重复问题;

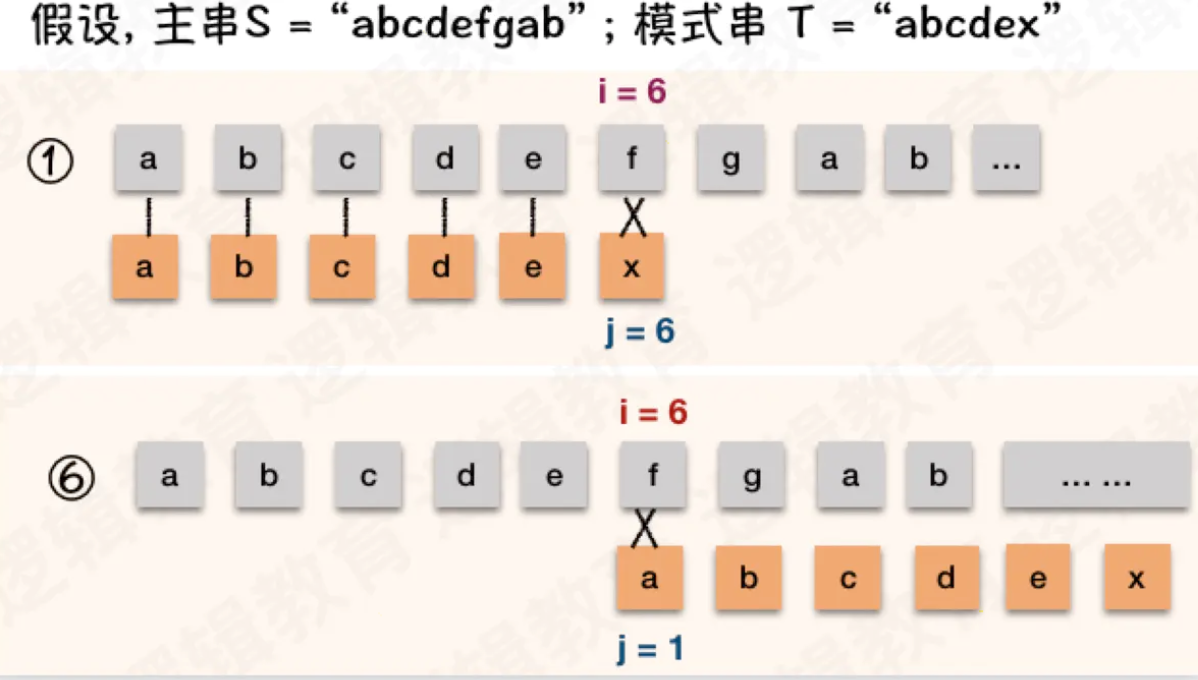
如上图,由于 T = "abcdex" 当中没有重复的数字, 所以 j 就由 6 变成了1;
而下图,由于 T = "abcabx". 前缀 "ab" 与最后的"x" 之前串的后缀 "ab" 是相等的. 所以就 j 就由 6 变成了 3;

总结1：

因此得出规律: j 值的多少取决于当前字符之前的串前后缀相似度;也就是在模式串的每个字符前面有多少个字符跟开头几个字符相同，那么j就等于多少

例如：

根据之前总结的K的求取规则! 可以根据相等的字符,换算出K值; 同时需要注意的是:

next数组是比较连续的前缀字符和后缀字符;
例如当j=6时,字符串"ababa", 最大前缀是"aba",后缀也是"aba".
当 j = 7时,字符串"ababaa",此时前缀是"a",后缀是"a". 不要误以为是"ab";

情况4：

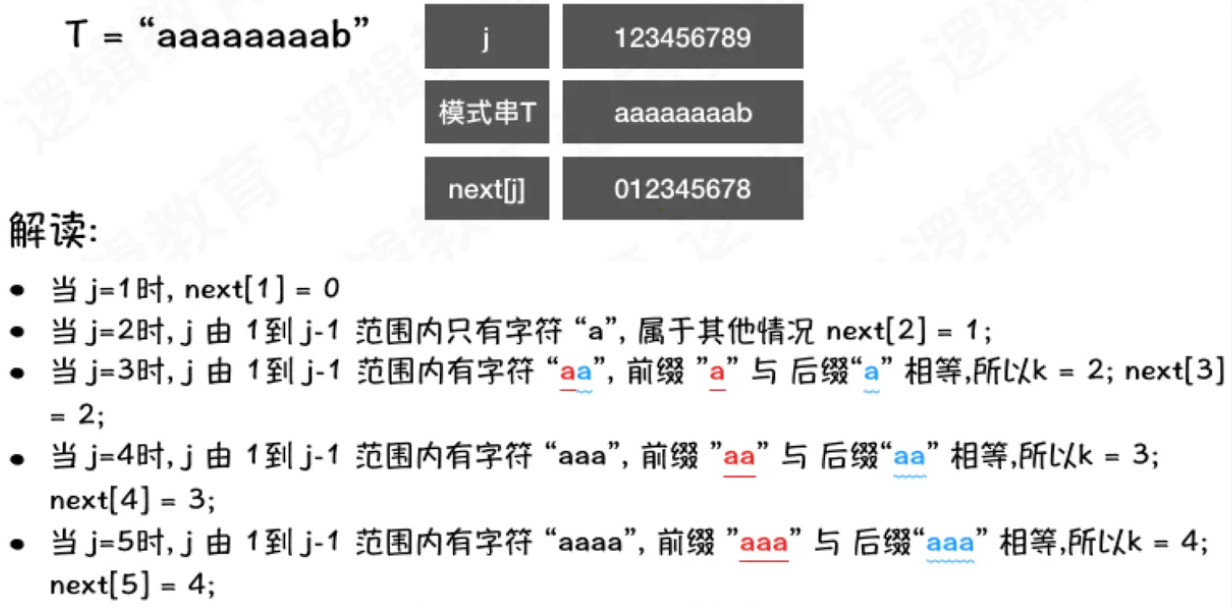
在这样的情况下,需要注意刚刚发生的重叠情况就可以了.

KMP模式匹配算法实现

计算子串T的next数组:求解next数组其实就是在求解字符串的回溯位置; KMP next数组的回溯位置求解过程模拟

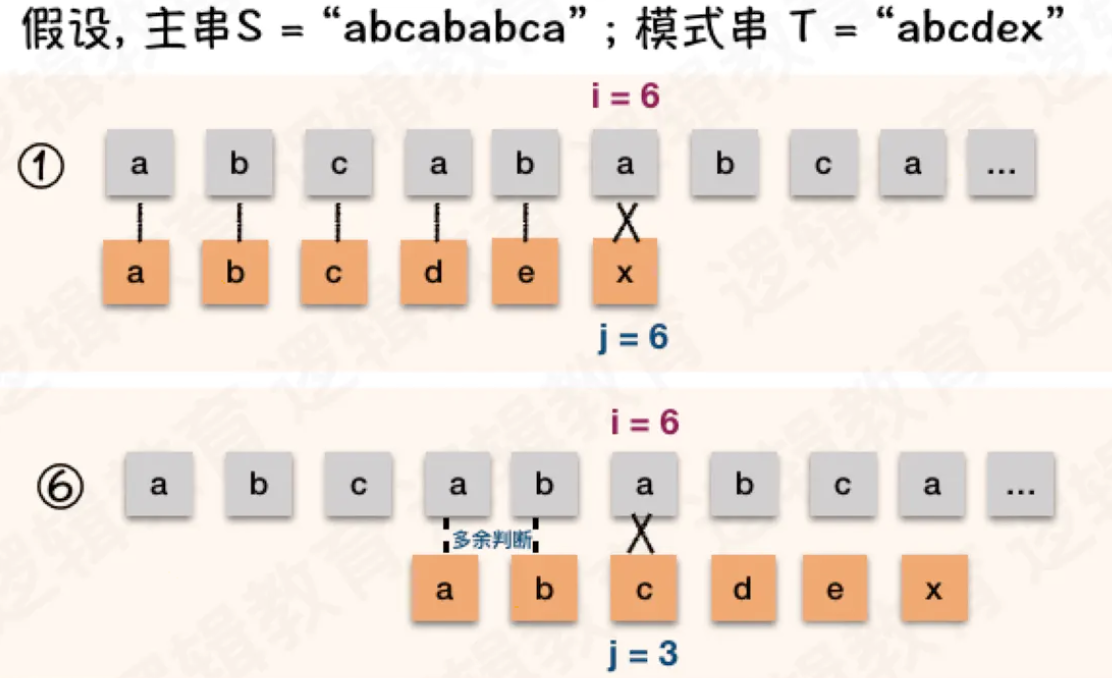
假设, 主串S = “abcababca” ; 模式串 T = “abcdex”

根据刚刚的公式的推演过程,我们其实非常情况next数组的应该是 011111 . 但是我们如何利用代码来求解出next数组了?

011111,意味着什么.

意味着其实模式串中abcdex 根本没有可以便于回溯的地址.也就是当主串与模式串不匹配时,都需要从第1的位置上重新比较;

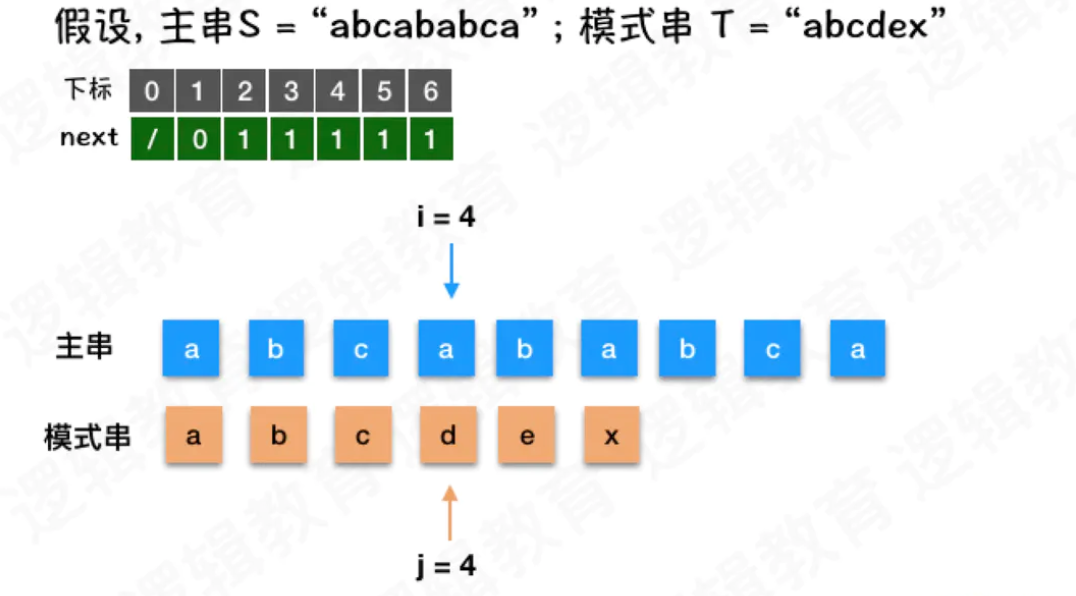
比如 abcababca 比较 abcdex 当比较到第4个位置是发现不匹配. 而此时主串的索引不变;

模式串的索引j当时等于4. 而此时发现不匹配,则要进行回溯. 那么应该回溯到哪里了?

j = next[j] ; j = 1; 也就是把abcbabca 的第4个字符与模式串的第1个字符串重新开始比较;

首先默认next[1] = 0; 表示它需要从0开始遍历;

接下来设计2个索引下标 i = 0, j = 1;

i 用于求解回溯的地址, 而j用于模式串的遍历

如果出现 i = 0,就是表示此时在模式串中并没有出现它相同的字符, 需要记录此时的回溯地址地址为1; next[j] = 1; 表示需要把从模式串的第一个字符开始比较;

如果T[i] == T[j] 表示此时已经出现了模式串中有重叠字符,则回溯地址next[j] = i;

如果既没有出现 i = 0,且 T[i] == T[j] 表示此时从[i,j]这个范围没有出现回溯位置的调整,我们则把 i 回溯到next[i] 的位置;

这个过程我们通过图例来分析! 这是KMP算法.也是众多匹配算法中最为难以理解的算法;

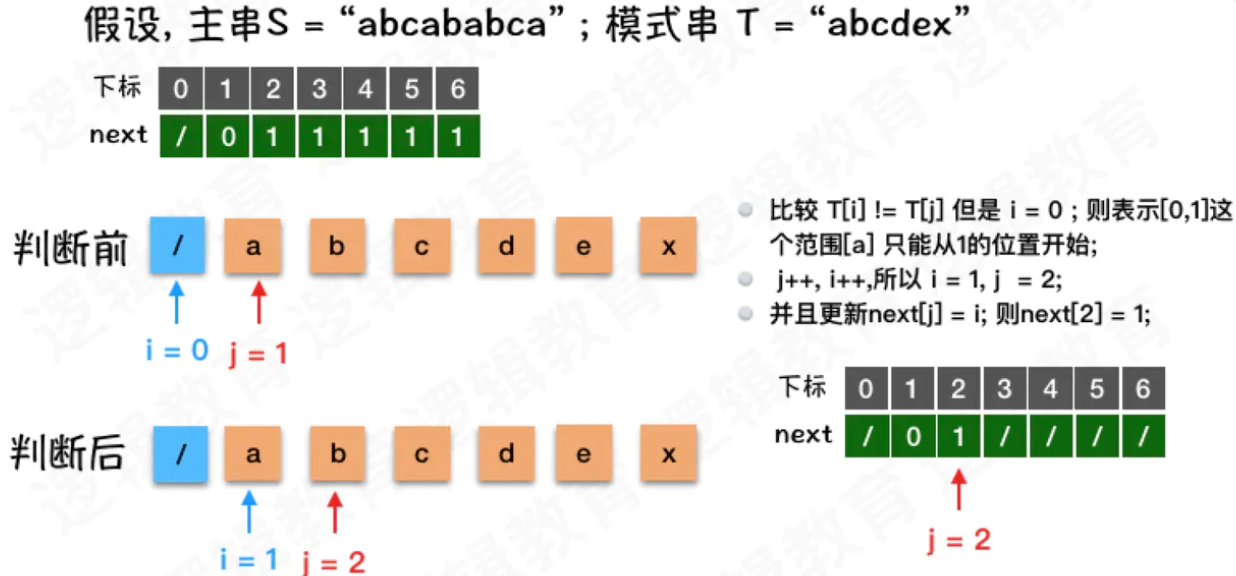
此时在 i = 0,且j = 1的情况下.也是就是我们要找到[0,1]这个范围的字符 a 是否存储需要回溯的情况.
而这是只有字母 a,并且当前 i = 0, - 所以如果主串和模式串匹配是,遇到第2个字符就不相配.
那么就应该讲主串后移1位,并且与模式串重新的第1位开始重新匹配计算;
但是此时i=0,j = 1; 所以我们应该i++,j++;
并且将next[j] = i; 所以此时`next[2] = 1;
表示,当j=2时,发现字符不匹配.需要把控制模式串比较的下标索引回溯到1. 从第一个字符重新开始比较;

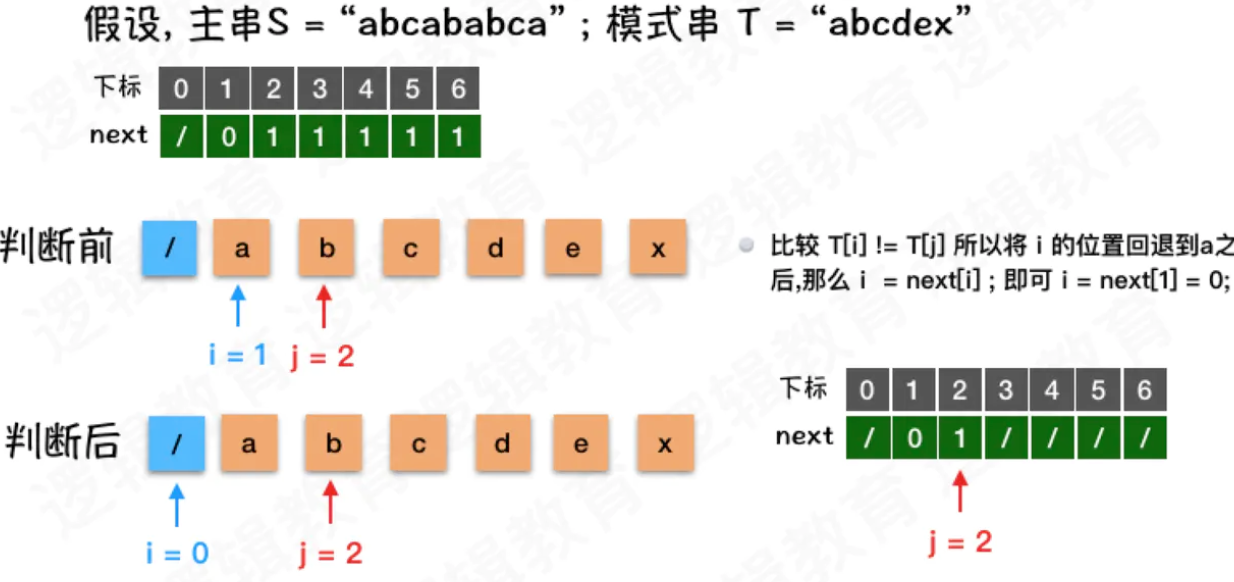
此时i = 1,j = 2，明白此时在[0,2]范围内,没有可以回溯的合理位置;
所以将i回退到next[1]. 也就是 i = next[i];
那么如果i = 1,next[1] = 0;也就是0的位置; 0就意味着我们需要下一个字符进行比较时,我们需要头开始比较;
那么如果是 next[i] 等于其他位置,表示把i回溯到其他位置. 而只有i有可回溯的可能性才会回溯到其他位置.

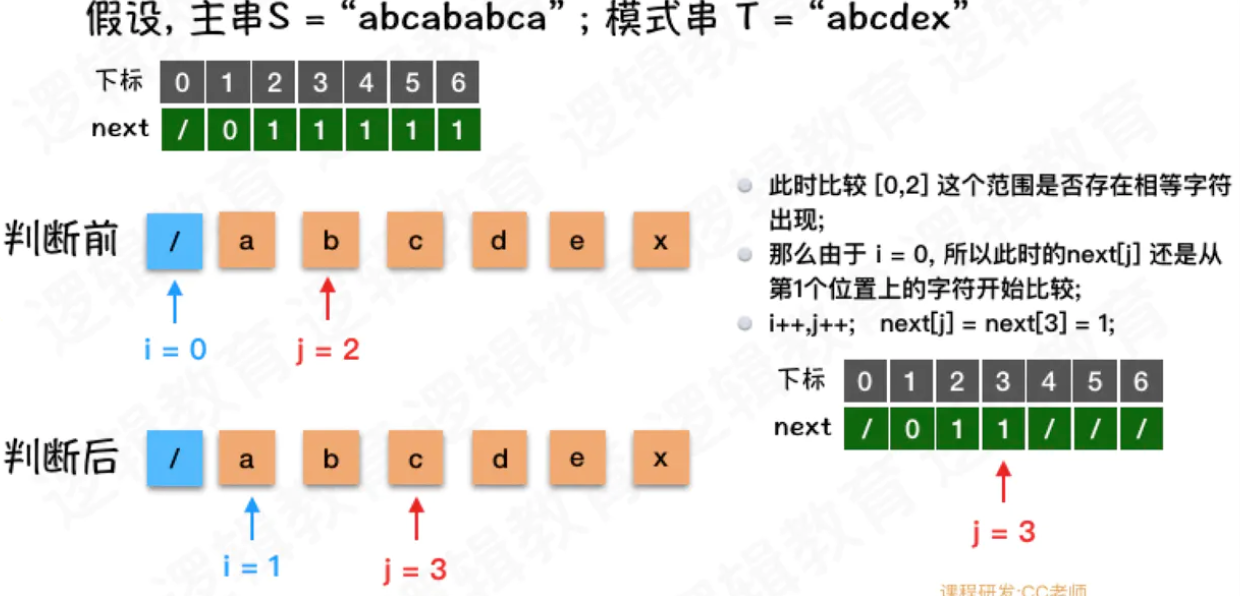
此时由于 i = 0, 那么就意味着如果需要从头开始比较;
那么头的位置指的是 1. 所以i++,j++; 因为这是当j = 3时, 如果不匹配需要回溯到开始的位置. 所以j 也是要➕➕ 的;
同时next[j] = i; 所以next[3] = 1;

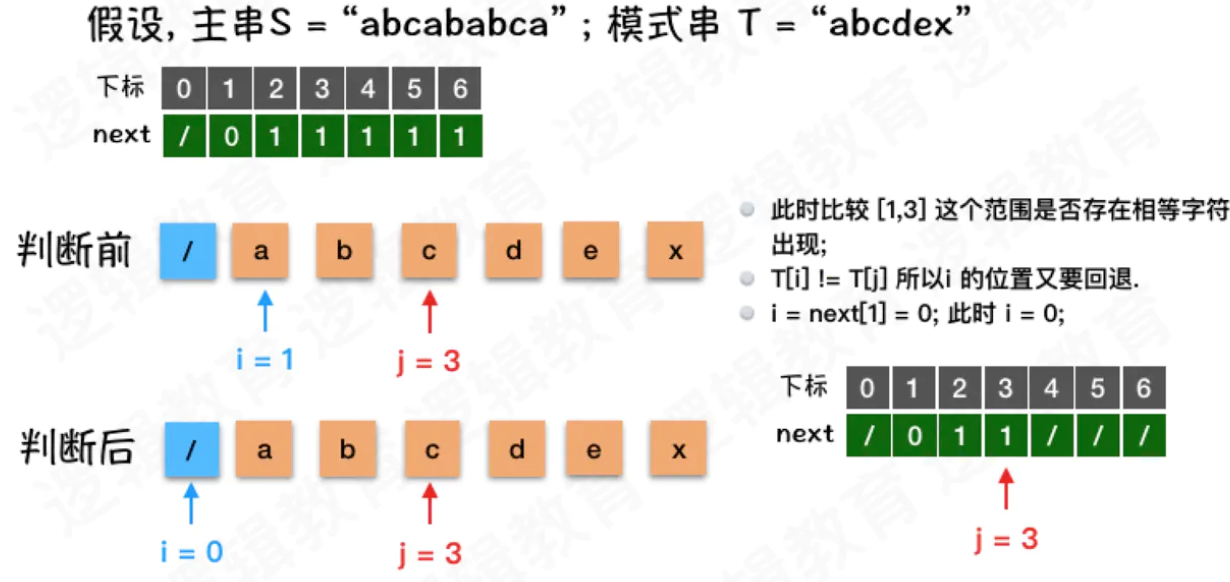
此时i = 1, j = 3;
那么我们要看看这个范围内是否出现回溯的可能性;
而此时T[i] != T[j], a != c ,所以此时应该回到开始的位置;
也就是 i = next[i]; 此时 i 等于0 .
表示下一次的比较,要重头开始;

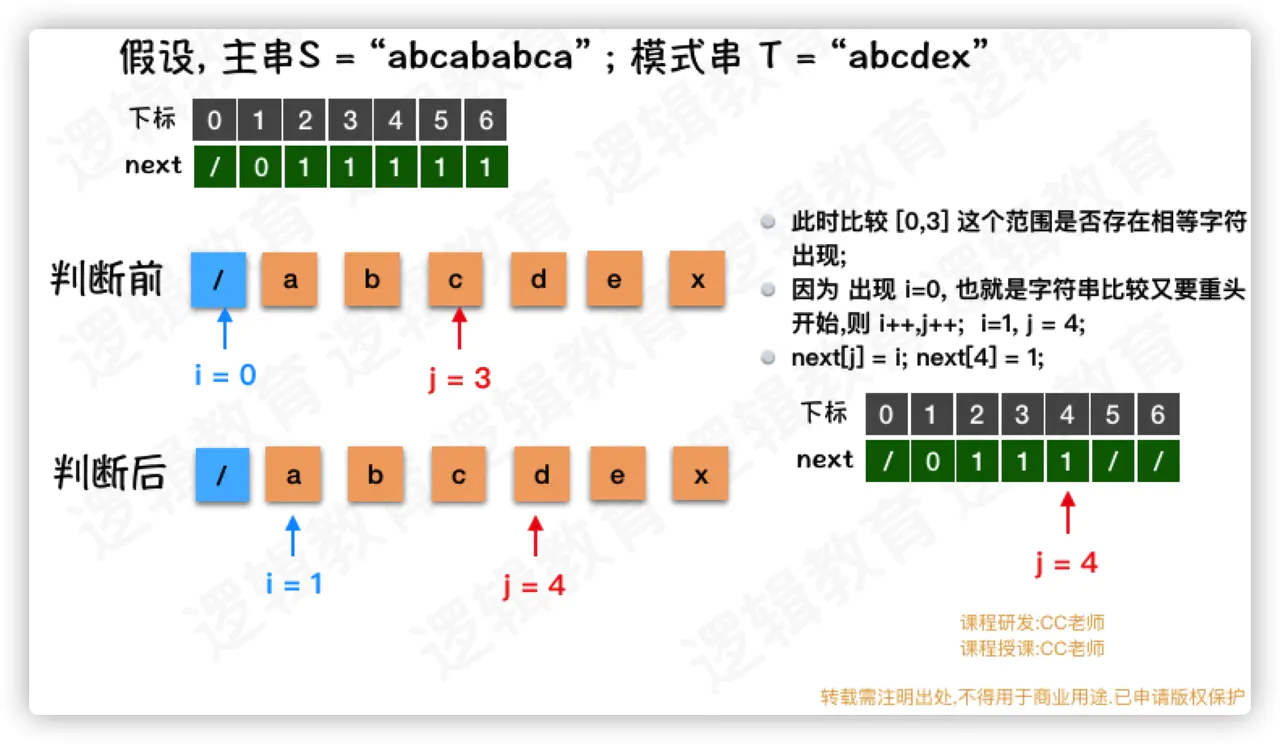
此时 i = 0,也就意味着.当j = 4时, 是需要从头开始比较;
那么 i++,j++,同时next[j] = i;
此时,i = 1,j = 4, next[4] = 1;

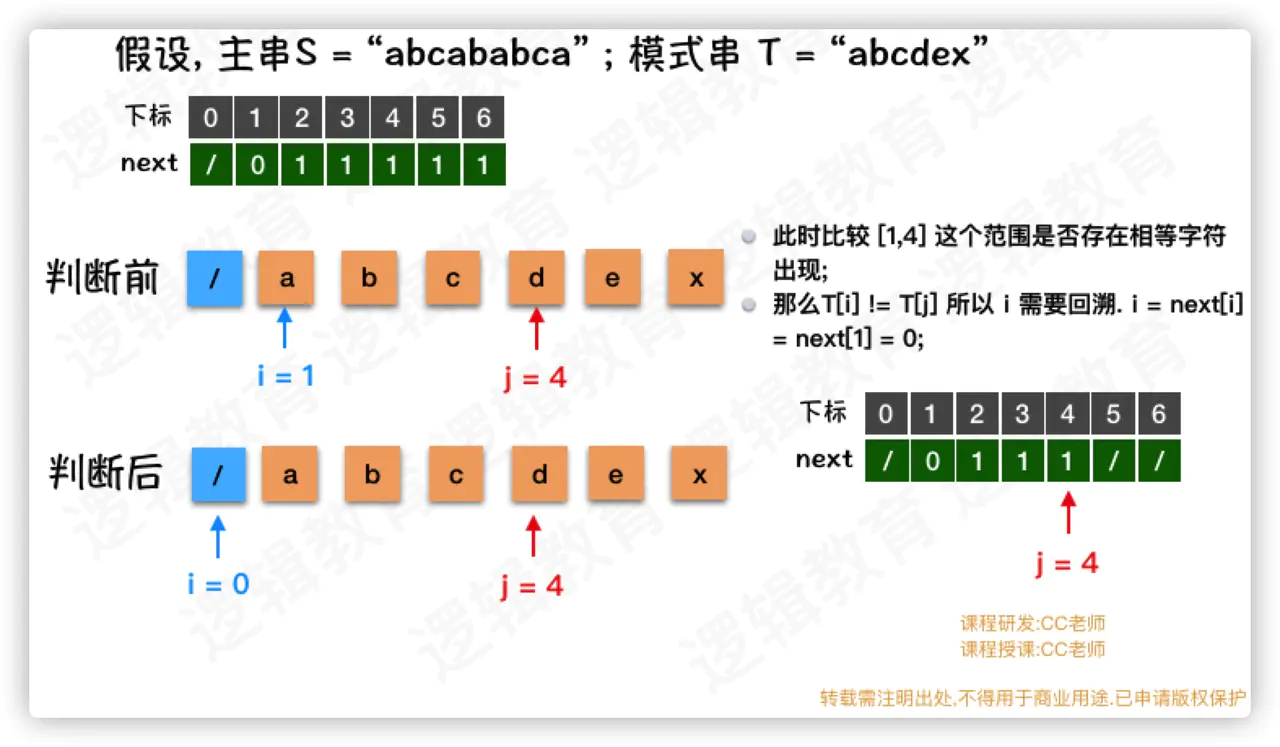
当j = 4时候，i=1，依然不匹配需要从头开始找，所以next[4]=1

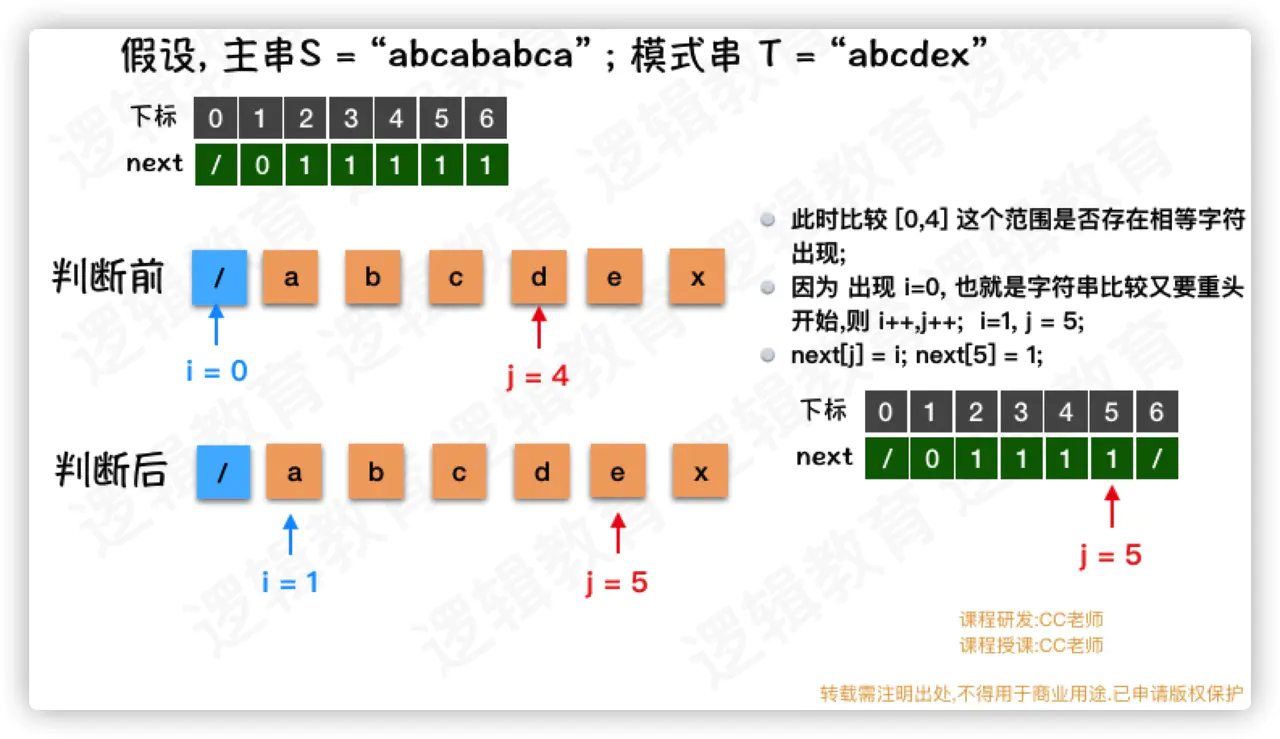
当j = 5时候，i=1，依然不匹配需要从头开始找，所以next[5]=1

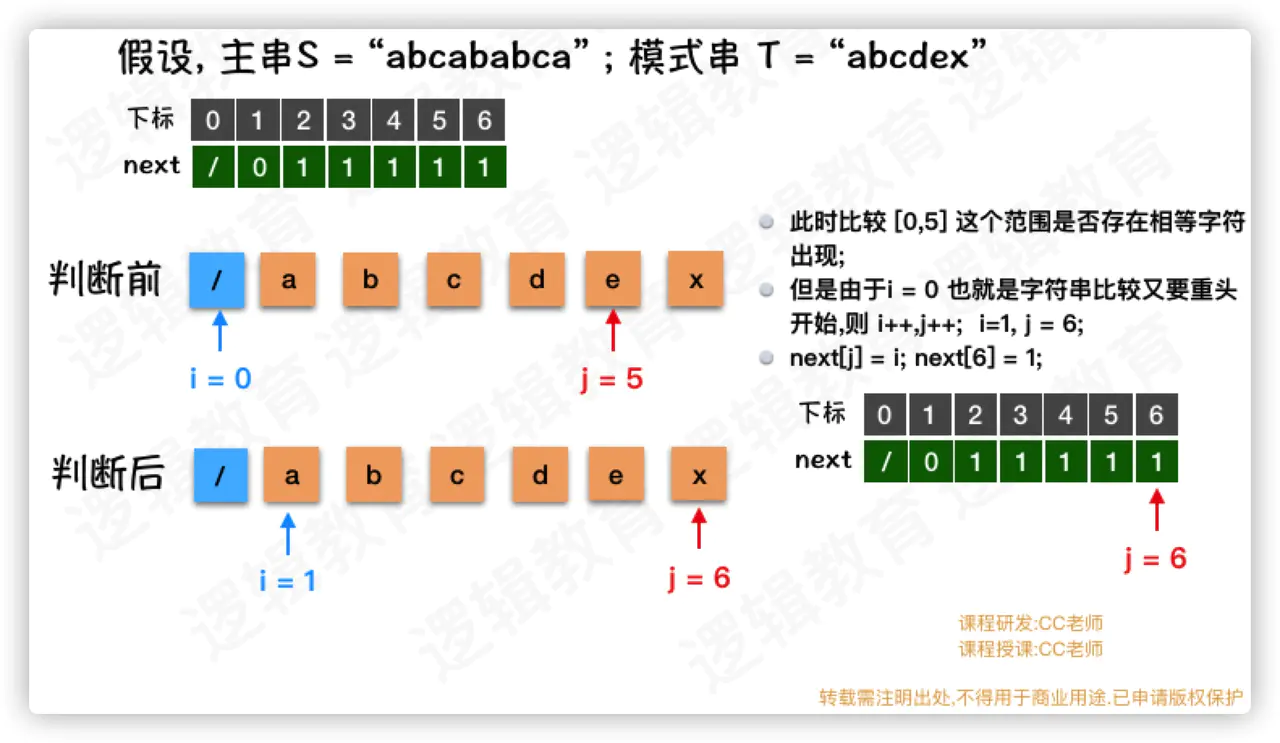
此时 j = 6. 循环条件不能满足,则退出循环;
在j等于1到5的时候, 都是需要从头开始比较; 那么 i++,j++,同时next[j] = i;

总结求解next数组

在求解next数组的4种情况:

默认next[1] = 0;
当 i=0时,表示当前的比应该从头开始.则i++,j++,next[j] = i;
当 T[i] == T[j] 表示2个字符相等,则i++,j++.同时next[j] = i;
当 T[i] != T[j] 表示不相等,则需要将i 退回到合理的位置. 则 i = next[i];

那么 next 数组如何应用到KMP 的查找中了?

当字符比较不匹配时, 如果是暴力查找法时;

当发现主串与模式串在 i = 4,j = 4时不匹配. 那么下一次比较

则是i = 2,j = 1,重新开始比较;

当使用 KMP 时, i = 4, j = 4 时发现不匹配,则进行下一次比较时.

i 保留 4 的位置,不需要回退; 同时 j = next[j];

此时发现 next[j] = 1,那么则让 j = 1.开始新的一轮比较'

KMP算法之next数组求解

//----KMP 模式匹配算法---
//1.通过计算返回子串T的next数组;
//注意字符串T[0]中是存储的字符串长度; 真正的字符内容从T[1]开始;
void get_next(String T,int *next){
    int i,j;
    j = 1;
    i = 0;
    next[1] = 0;
    //abcdex
    //遍历T模式串, 此时T[0]为模式串T的长度;
    printf("length = %d\n",T[0]);
    while (j < T[0]) {
        printf("i = %d j = %d\n",i,j);
        if(i ==0 || T[i] == T[j]){
            //T[i] 表示后缀的单个字符;
            //T[j] 表示前缀的单个字符;
            ++i;
            ++j;
            next[j] = i;
            printf("next[%d]=%d\n",j,next[j]);
        }else
        {
            //如果字符不相同,则i值回溯;
            i = next[i];
        }
    }
}

KMP 查找算法(1)

int count = 0;
//KMP 匹配算法
//返回子串T在主串S中第pos个字符之后的位置, 如不存在则返回0;
int Index_KMP(String S,String T,int pos){
    
    //i 是主串当前位置的下标准,j是模式串当前位置的下标准
    int i = pos;
    int j = 1;
    
    //定义一个空的next数组;
    int next[MAXSIZE];
    
    //对T串进行分析,得到next数组;
    get_next(T, next);
    count = 0;
    //注意: T[0] 和 S[0] 存储的是字符串T与字符串S的长度;
    //若i小于S长度并且j小于T的长度是循环继续;
    while (i <= S[0] && j <= T[0]) {
        
        //如果两字母相等则继续,并且j++,i++
        if(j == 0 || S[i] == T[j]){
            i++;
            j++;
        }else{
            //如果不匹配时,j回退到合适的位置,i值不变;
            j = next[j];
        }
    }
    
    if (j > T[0]) {
        return i-T[0];
    }else{
        return 0;
    }
    
}

KMP 模式匹配算法优化

KMP 算法也是有缺陷的. 比如,如果我们的主串 S = "aaaabcde",模式串T = "aaaaax". 其中 next 数组就是 012345;

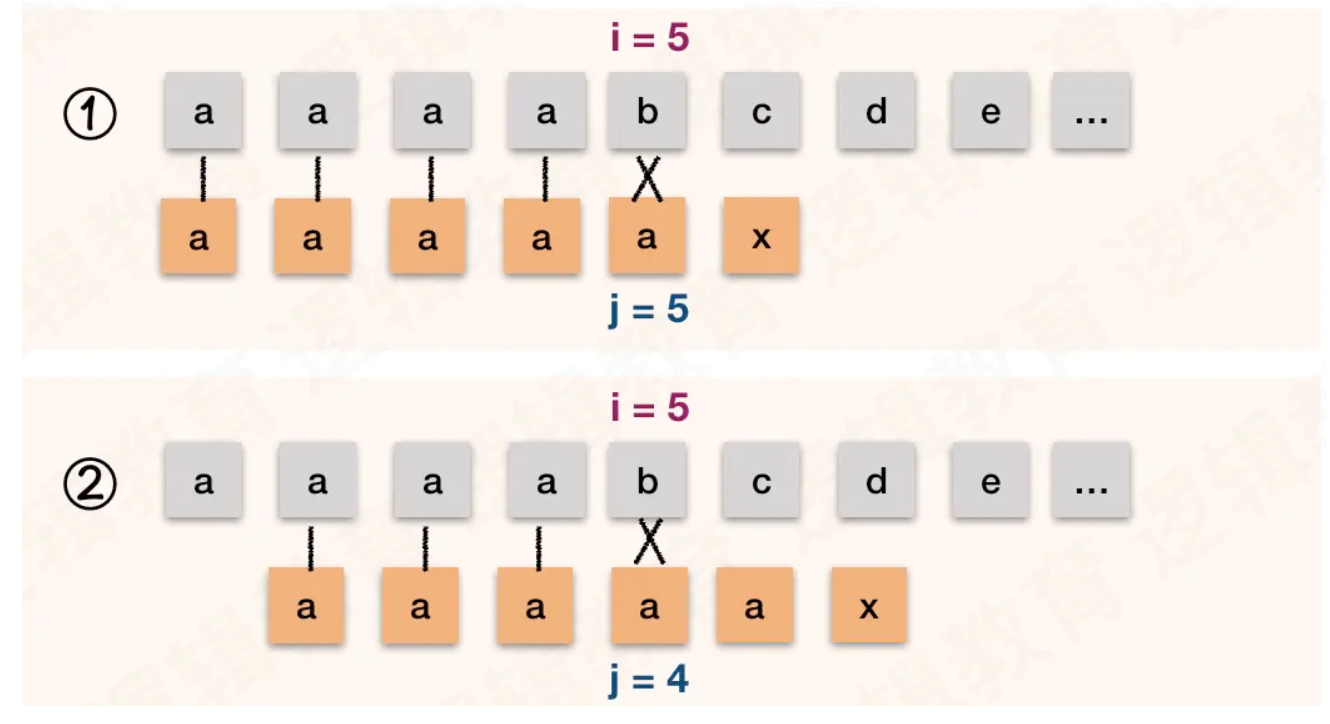
当开始匹配时, 当 i = 5, j = 5 时, 我们发现字符 "b" 与字符 "a" 不相等时, 如图① . 因此 j = next[5] = 4.

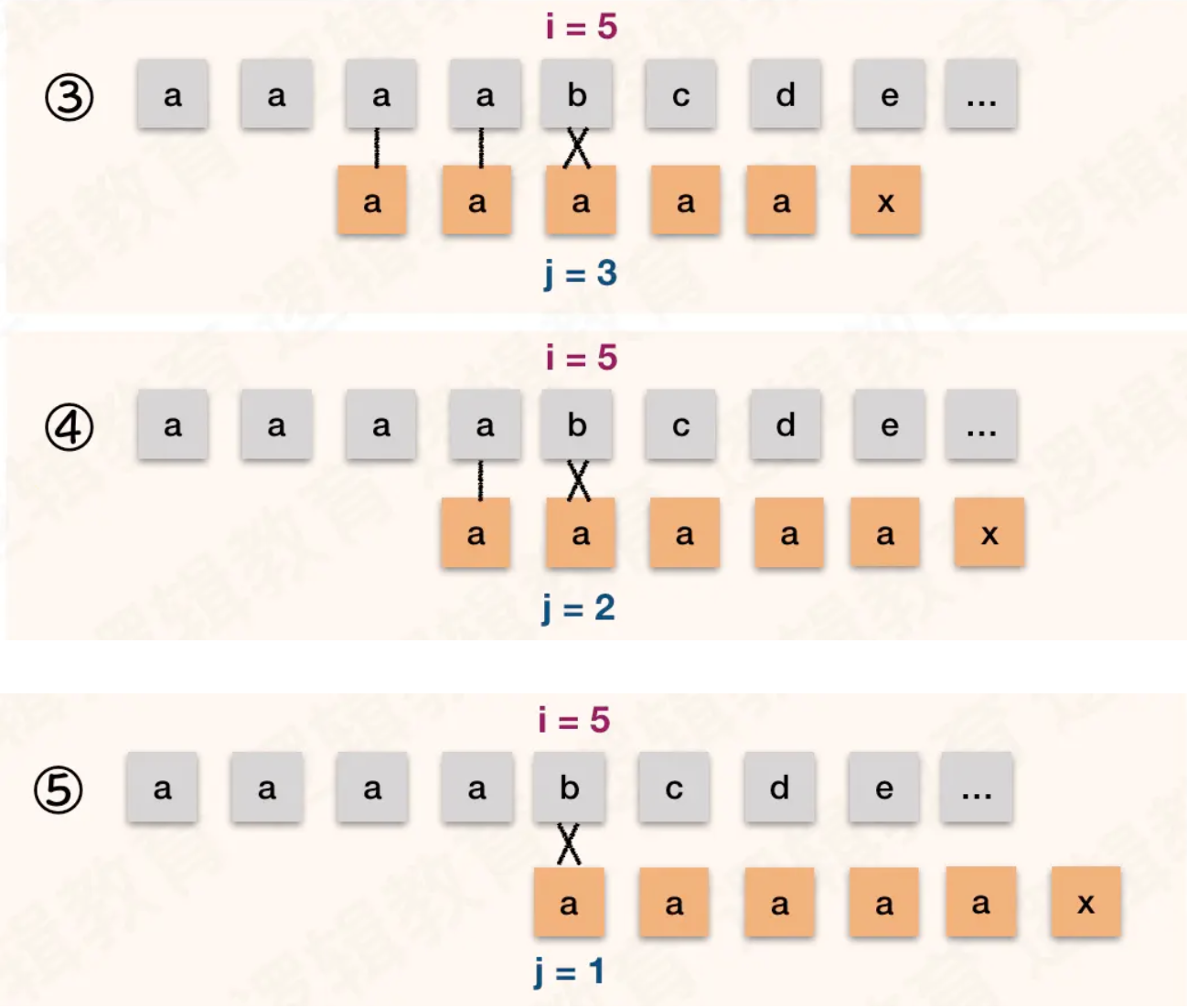
那么此时就如图②. 此时字符 "b" 与第4个位置上的 "a" 依然不等; j = next[4] = 3; 如图③

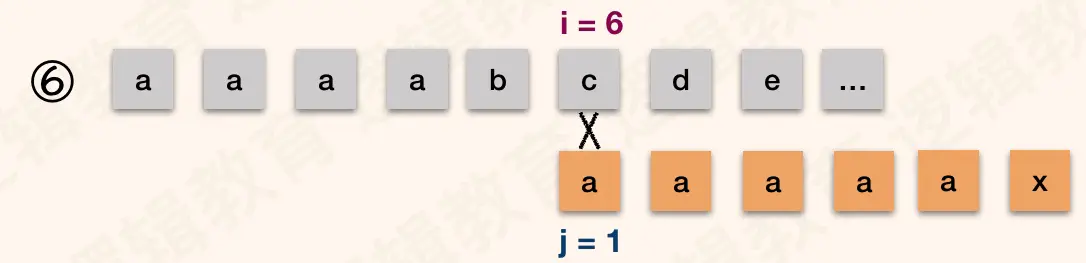
以此内推. 如图④⑤; 当 j = next[1] = 0时,根据算法,此时 i++,j++; 得到i = 6,j = 1. 如图⑥;

其实,在比较的过程发现当中②③④⑤步骤的回溯比较都是多余的判断;
由于 T 串的第二,三,四,五位置的字符都与首位 "a" 相等, 那么可以用首位 next[1] 的值去取代与它相等的字符后续的 next[j] 值. 那么我们来对 next 函数来进行改良;
next 数组= {0,1,2,3,4,5}如果要节省刚刚 ②③④⑤ 的无效比较则需要next 数组={0,0,0,0,0,5}

KMP 模式匹配next 数组的优化

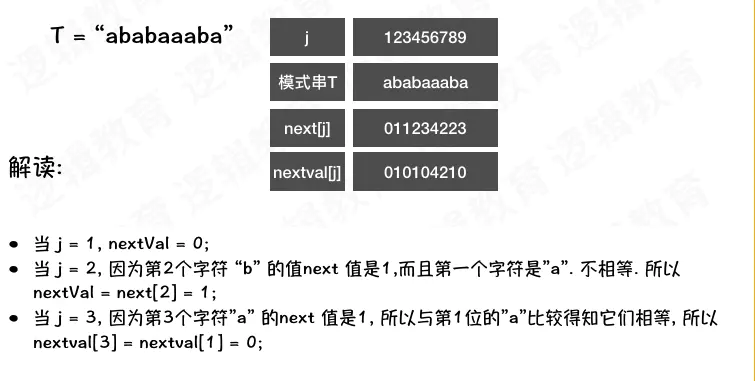
当 j = 1,nextVal = 0; 继续保持next[1]的逻辑;
当 j = 2时, 也就是当j = 2发生匹配错误, 那么由于第二个字符'b'的 next 值是1, 而且第一个字符是'a' .两者不相等.所以nextval[2] = next[2] = 1;

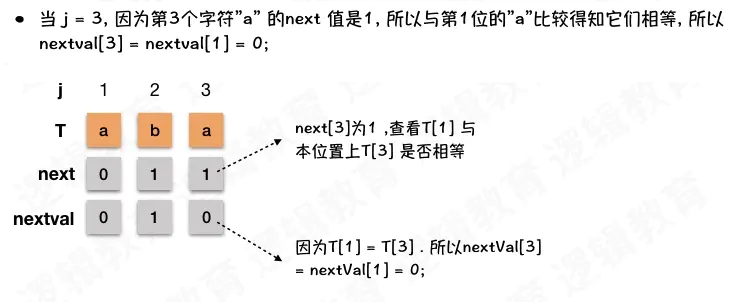
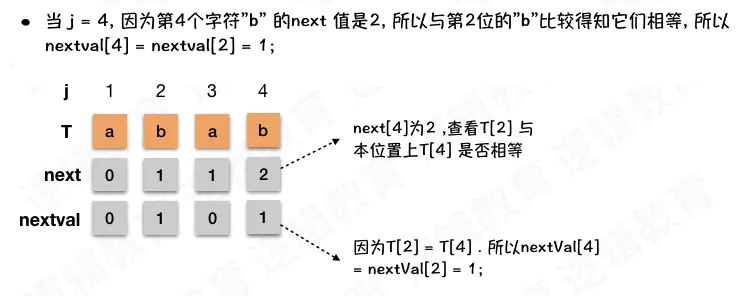
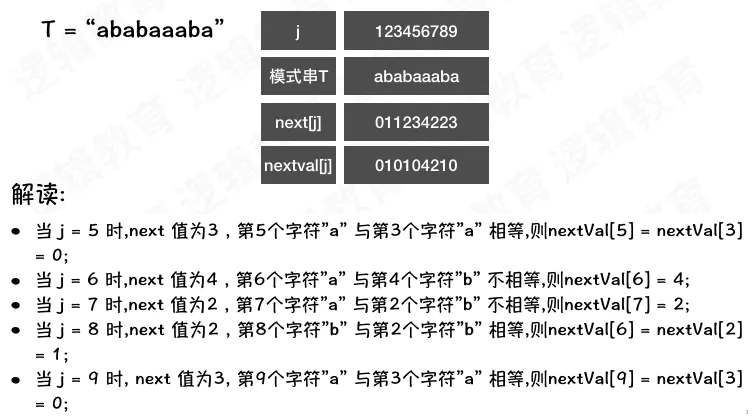
KMP_NextVal 数组逻辑在求解nextVal数组的5种情况:

1、默认nextval[1] = 0;
2、T[i] == T[j] 且++i,++j 后 T[i] 依旧等于 T[j] 则 nextval[i] = nextval[j]
3、i = 0, 表示从头开始i++,j++后,且T[i] != T[j] 则nextVal = j;
4、T[i] == T[j] 且++i,++j 后 T[i] != T[j] ,则nextVal = j;
5、当 T[i] != T[j] 表示不相等,则需要将i 退回到合理的位置. 则 i = next[i];

void get_nextVal(String T,int *nextVal){
    int i,j;
    i = 1;
    j = 0;
    nextVal[1] = 0;
    while (i < T[0]) {
        if (j == 0 || T[i] == T[j]) {
            ++j;
            ++i;
            //如果当前字符与前缀不同,则当前的j为nextVal 在i的位置的值
            if(T[i] != T[j])
                nextVal[i] = j;
            else
            //如果当前字符与前缀相同,则将前缀的nextVal 值赋值给nextVal 在i的位置
                nextVal[i] = nextVal[j];
        }else{
            j = nextVal[j];
        }
    }
}

数据结构和算法 - KMP算法