数据结构与算法之图的遍历

图的深度优先遍历

邻接矩阵遍历

• 分析邻接矩阵结构

  
  

• 根据上图我们知道，相连接的两个顶点的值为1，所以遍历图的时候需要判断两个顶点是否连接

• 使用一个数组来记录当前的顶点是否进行了遍历

• 代码实现逻辑

  
  

• 代码实现

  #include <stdio.h>
  #include <stdlib.h>
  #include "math.h"
  #include "time.h"
  
  #define TRUE 1
  #define FALSE 0
  
  typedef int Boolean; /* Boolean是布尔类型,其值是TRUE或FALSE */
  
  typedef char VertexType; /* 顶点类型应由用户定义 */
  typedef int EdgeType; /* 边上的权值类型应由用户定义 */
  
  #define MAXSIZE 9 /* 存储空间初始分配量 */
  #define MAXVEX 9
  
  typedef struct
  {
      VertexType vexs[MAXVEX]; /* 顶点表 */
      EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵，可看作边表 */
      int numVertexes, numEdges; /* 图中当前的顶点数和边数 */
  }MGraph;
  
  /*4.1 构建一个邻接矩阵*/
  void CreateMGraph(MGraph *G)
  {
      int i, j;
      
      //1. 确定图的顶点数以及边数
      G->numEdges=15;
      G->numVertexes=9;
      
      /*2.读入顶点信息，建立顶点表 */
      G->vexs[0]='A';
      G->vexs[1]='B';
      G->vexs[2]='C';
      G->vexs[3]='D';
      G->vexs[4]='E';
      G->vexs[5]='F';
      G->vexs[6]='G';
      G->vexs[7]='H';
      G->vexs[8]='I';
      
      /*3. 初始化图中的边表*/
      for (i = 0; i < G->numVertexes; i++)
      {
          for ( j = 0; j < G->numVertexes; j++)
          {
              G->arc[i][j]=0;
          }
      }
      
      /*4.将图中的连接信息输入到边表中*/
      G->arc[0][1]=1;
      G->arc[0][5]=1;
      
      G->arc[1][2]=1;
      G->arc[1][8]=1;
      G->arc[1][6]=1;
      
      G->arc[2][3]=1;
      G->arc[2][8]=1;
      
      G->arc[3][4]=1;
      G->arc[3][7]=1;
      G->arc[3][6]=1;
      G->arc[3][8]=1;
      
      G->arc[4][5]=1;
      G->arc[4][7]=1;
      
      G->arc[5][6]=1;
      
      G->arc[6][7]=1;
      
      /*5.无向图是对称矩阵.构成对称*/
      for(i = 0; i < G->numVertexes; i++)
      {
          for(j = i; j < G->numVertexes; j++)
          {
              G->arc[j][i] =G->arc[i][j];
          }
      }
  }
  #pragma mark - 定义bool类型的数组用来记录该顶点是否被遍历
  Boolean visit[MAXSIZE] = {FALSE};
  //从index顶点开始遍历
  void DFSVisit(MGraph map, int index){
      //设置成遍历过了
      visit[index] = TRUE;
      //打印当前遍历的顶点
      printf("当前遍历的顶点是：%c\n",map.vexs[index]);
      for (int i = 0; i<map.numVertexes; i++) {
          //递归遍历
          if (map.arc[index][i] == 1 && !visit[i]) {
              DFSVisit(map, i);
          }
      }
      
  }
  
  int main(int argc, const char * argv[]) {
      // insert code here...
      printf("Hello, World!\n");
      MGraph map;
      CreateMGraph(&map);
      for (int i = 0; i<map.numVertexes; i++) {
          if (!visit[i]) {
              DFSVisit(map, i);
          }
      }
      return 0;
  }
  

邻接表的遍历

• 邻接表的结构

  
  

• 邻接表的代码实现逻辑思路

  
  

• 代码实现（核心代码）

  #pragma mark - 定义bool类型的数组用来记录该顶点是否被遍历
  Boolean visit[MAXSIZE] = {FALSE};
  //从index顶点开始遍历
  void DFSVisit(GraphAdjList map, int index){
      //设置成遍历过了
      visit[index] = TRUE;
      //打印当前遍历的顶点
      printf("当前遍历的顶点是：%c\n",map->adjList[index].data);
      EdgeNode *temp = map->adjList[index].firstedge;
      while (temp) {
          if (!visit[temp->adjvex]) {
              DFSVisit(map, temp->adjvex);
          }
          temp = temp->next;
      }
      }
  int main(int argc, const char * argv[]) {
      // insert code here...
      printf("Hello, World!\n");
      MGraph G;
      GraphAdjList GL;
      CreateMGraph(&G);
      CreateALGraph(G,&GL);
      for (int i = 0; i<GL->numVertexes; i++) {
          if (!visit[i]) {
              DFSVisit(GL, i);
          }
      }
      return 0;
  }
  
  

广度优先遍历

广度优先遍历的特点

• 把根节点放到队列的末尾
• 每次从队列的头部取出一个元素，查看这个元素下的所有的下一级元素，把它们放在队列的末尾，并把这个元素记为它下一级元素的前驱
• 找到所要找到的元素时结束程序
• 如果遍历整个树还没有找到则结束程序

广度优先遍历的图示结构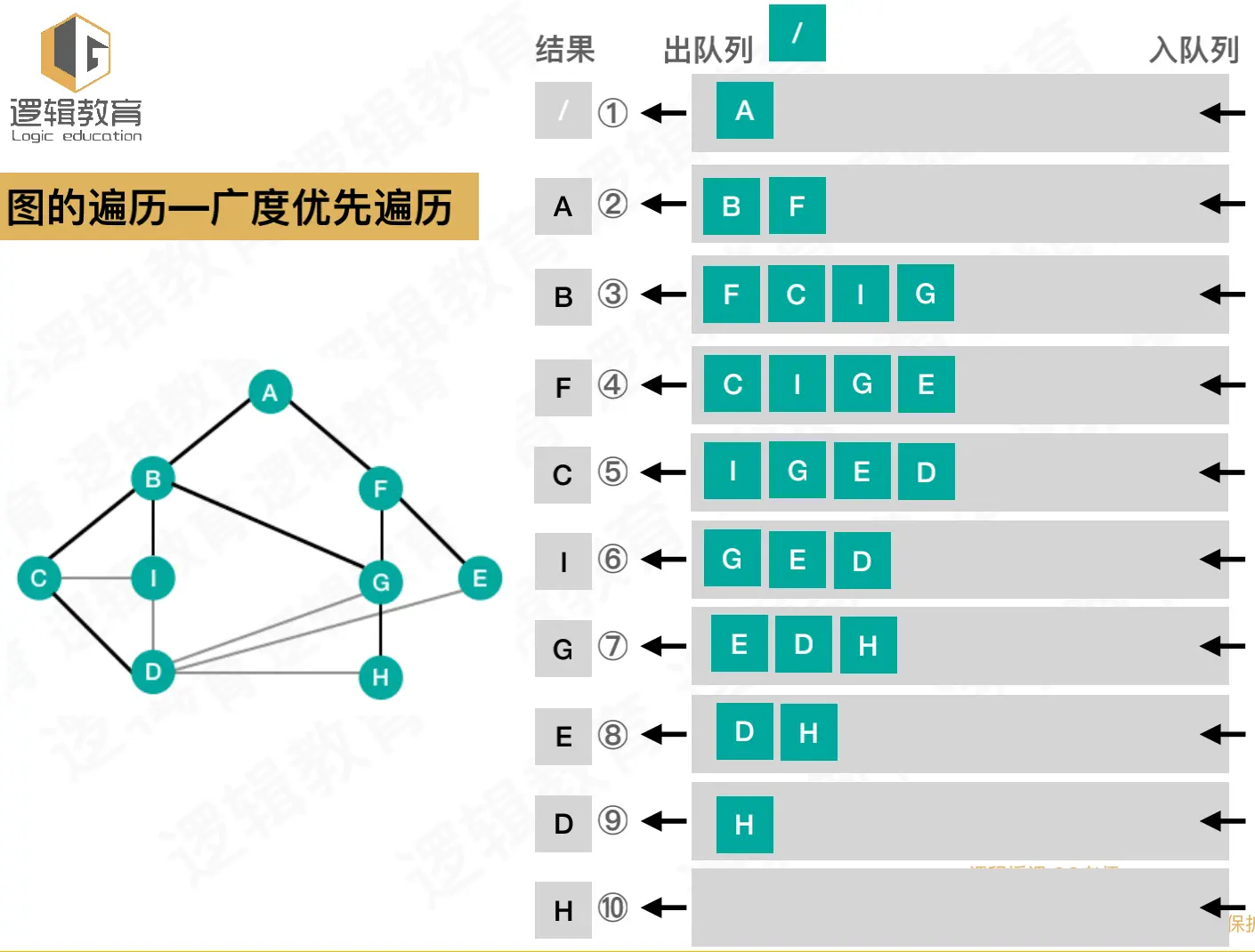

邻接矩阵遍历代码实现

Boolean visit[MAXSIZE] = {FALSE};
void BFSVisit(MGraph Map){
    Queue Q;
    InitQueue(&Q);
    //遍历顶点
    for (int i = 0; i<Map.numVertexes; i++) {
        if (!visit[i]) {//当前顶点还没与遍历
            visit[i] = TRUE;
            //打印当前的顶点
            printf("当前遍历的顶点是：%c\n",Map.vexs[i]);
            //入栈
            EnQueue(&Q, i);
            while (!QueueEmpty(Q)) {
                //出队
                DeQueue(&Q, &i);
                for (int j = 0; j < Map.numVertexes; j++) {
                    if(Map.arc[i][j] == 1 && !visit[j])
                    {    visit[j] = TRUE;
                        printf("当前遍历的顶点是：%c\n",Map.vexs[j]);
                        EnQueue(&Q, j);
                    }
                }
            }
        }
    }
}

int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, World!\n");
    MGraph Map;
    CreateMGraph(&Map);
    BFSVisit(Map);
    printf("\n");
    return 0;
}

邻接表遍历代码实现

Boolean visit[MAXSIZE] = {FALSE};
void BFSVisit(GraphAdjList Map){
    //创建结点
    EdgeNode *p;
    Queue Q;
    InitQueue(&Q);
    for (int i = 0; i<Map->numVertexes; i++) {
        if (!visit[i]) {
            visit[i] = TRUE;
            EnQueue(&Q, i);
            printf("当前遍历的顶点是：%c\n",Map->adjList[i].data);
              
            while (!QueueEmpty(Q)) {
                DeQueue(&Q, &i);
                p = Map->adjList[i].firstedge;
                while (p) {
                    if (!visit[p->adjvex]) {
                        visit[p->adjvex] = TRUE;
                        printf("当前遍历的顶点是：%c\n",Map->adjList[p->adjvex].data);
                        EnQueue(&Q, p->adjvex);
                    }
                    p = p->next;
                }
            }
        }
    }
}