数据结构与算法之哈夫曼编码当我们计算学生分数分布范围的时候我们可能会这样设计代码，当数量集不大的时候计算效率差别不大，但

引入哈夫曼思想

如下图所示，

当我们计算学生分数分布范围的时候我们可能会这样设计代码，当数量集不大的时候计算效率差别不大，但是当数量集比较大的时候效率就比较低了，比如我们找大于90分的分布范围，需要多做几次判断才可以。因此我们引出哈夫曼编码的思想来解决问题

哈夫曼编码是如何思考的

给学生成绩分布添加比重，下图是没有添加权重的
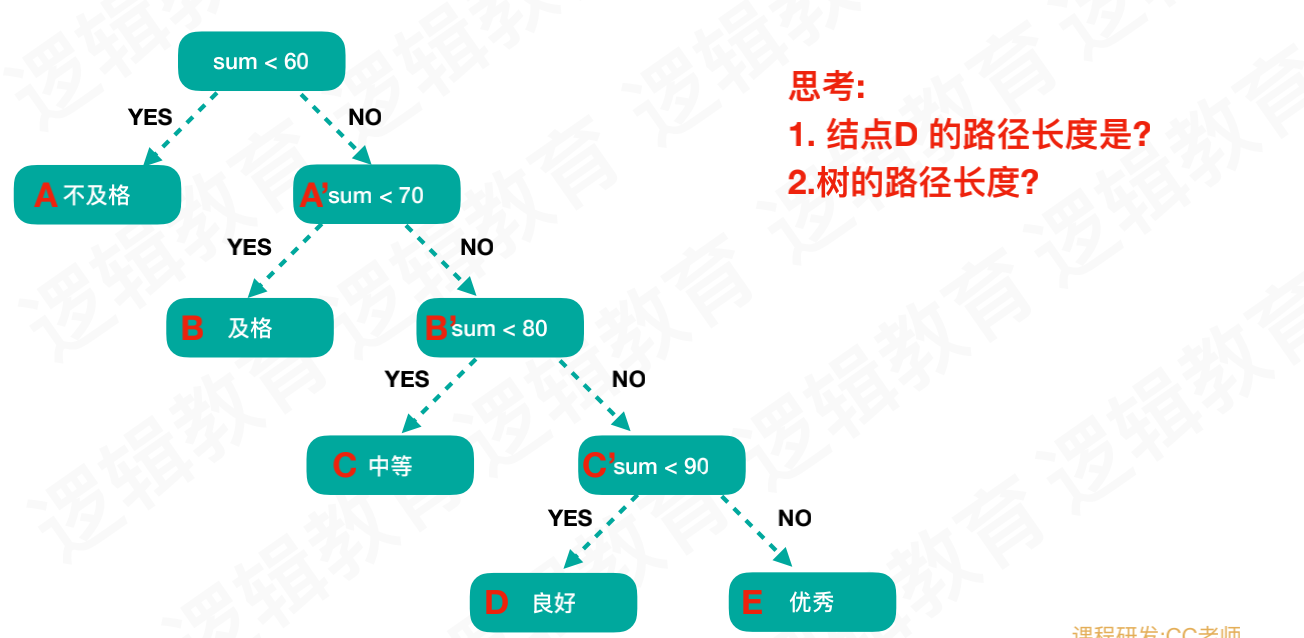
添加权重后的大小
此时wpl的大小是315，我们要使WPL值最小才能更好的优化该问题
优化WPL值，第一种
第二种优化
比较两种优化WPL我们可以得知第二种优化更好，第二种的方法是把权重比最小的看成是二叉树的叶子结点，比如A、E，然后A、E结点的权重之和变为N1（15）跟剩余的结点权重比较，然后发现B（15）结点的权重此时最小，然后N1跟B组合成新的结点，依次类推。注意的是同一层的结点，权重小的在左侧

利用哈夫曼编码来对发送信息进行编码

如下图所示，将发送的内容进行优化处理

哈夫曼编码分析

根据字母出现的概率（这个概率是大数据统计的结果，直接拿来使用的）进行排序
如上图中的5、8、15、15、27、30分别对应着F、B、C、D、A、E的权重值
根据权重值最小的F、B构造二叉树的结构，
根据新生成的结点N1（13）的权重与剩余结点的权重，继续构造二叉树结构，注意左节点的权重值比右节点小
依次类推剩余的步骤
最终生成二叉树如下图所示
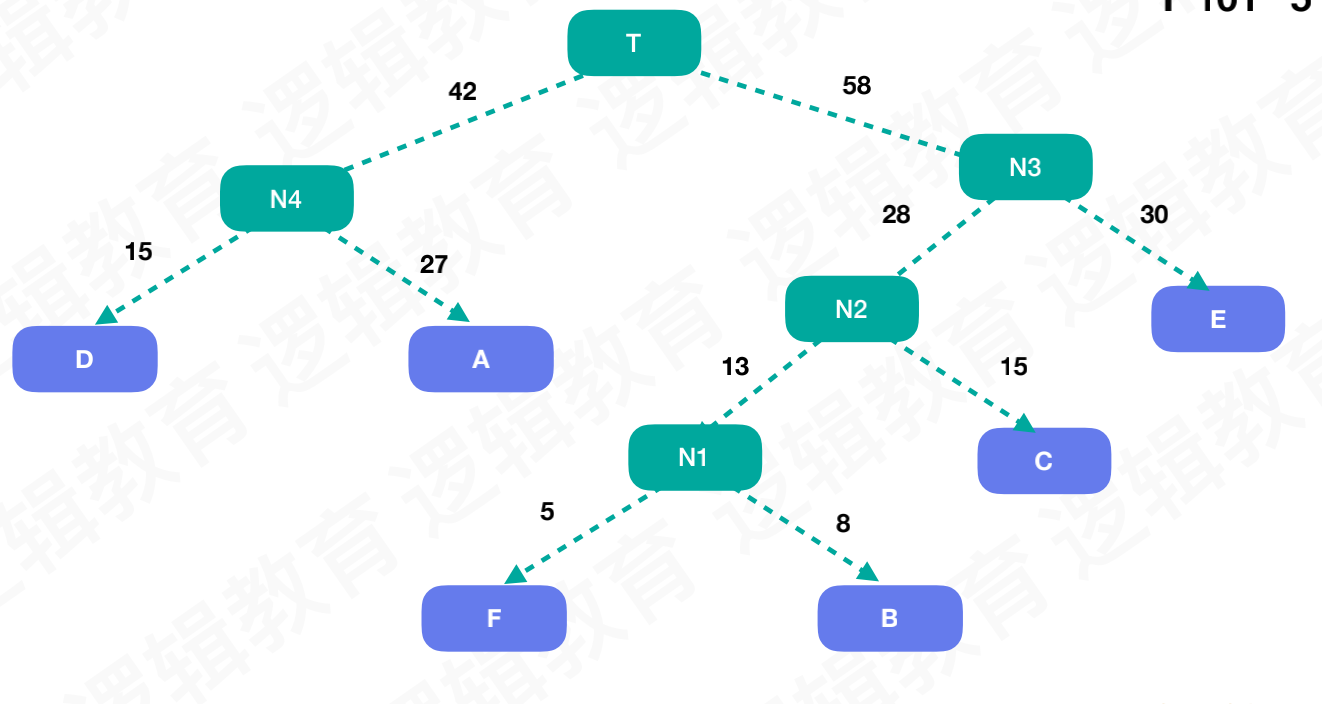
重新调整字母的权重路径，左孩子路径为0，右孩子为1，结果如下图所示
哈夫曼编码后的字符长度为
哈夫曼编码步骤总结
实现哈夫曼树思路

初始化哈夫曼树
循环不断找到结点中最小的两个结点值，然后加入到哈夫曼树中

哈夫曼编码实现思路

获取根据权值构建的哈弗曼树
循环遍历[0,n]个结点
创建临时结点temp，从根节点开始对temp开始编码，左孩子为0，右孩子为1
将编码后的结点存储haffCode[i]
设置haffCode[i]的开始位置以及权值

哈弗曼编码代码实现

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
const int MaxValue = 10000;//初始设定的权值最大值
const int MaxBit = 4;//初始设定的最大编码位数
const int MaxN = 10;//初始设定的最大结点个数

typedef struct HaffNode{
    int weight;//权重
    int flag;//是否处理过的标识，0表示没有处理，1表示处理过了
    int parent;//双亲结点的下标
    int leftChild;//左孩子的下标
    int rightChild;//右孩子的下标
}HaffNode;

typedef struct Code//存放哈夫曼编码的数据元素结构
{
    int bit[MaxBit];//数组
    int start;  //编码的起始下标
    int weight;//字符的权值
}Code;
#pragma mark - 根据权重创建哈夫曼树
void CreatHaffmanTree(int weight[], int n, HaffNode *nodeTree) {
    //weight[]为权重数组，n为结点个数，nodeTree是哈弗曼树
    int j,m1,m2,x1,x2;
    for (int i = 0; i<2*n - 1; i++) {//n个叶子结点有2n—1个结点
        if (i<n) {//叶子结点设置权重
            nodeTree[i].weight = weight[i];
        }else{
            nodeTree[i].weight = 0;
        }
        nodeTree[i].parent = 0;
        //设置成都未处理
        nodeTree[i].flag = 0;
        nodeTree[i].leftChild = -1;
        nodeTree[i].rightChild = -1;
    }
    //构造哈夫曼树的n-1个非叶子结点
    for (int i = 0; i<n-1; i++) {
        m1 = m2 = MaxValue;
        x1 = x2 = 0;
        for (j = 0; j<n + i; j++) {//找出结点中权重最小的两个结点
            if (nodeTree[j].weight < m1 && nodeTree[j].flag == 0) {
                m2 = m1;
                x1 = x2;
                m1 = nodeTree[j].weight;
                x1 = j;
            }else if (nodeTree[j].weight < m2 && nodeTree[j].flag == 0){
                m2 = nodeTree[j].weight;
                x2 = j;
            }
        }
        //将两个权重最小结点（子树）合并成一个结点（子树）
        nodeTree[x1].parent = n + i;
        nodeTree[x2].parent = n + i;
        //将最小的两个结点设置成已经处理了
        nodeTree[x1].flag = 1;
        nodeTree[x2].flag = 1;
        //给新生成的结点赋值权重
        nodeTree[n + i].weight = m1 + m2;
        //或这样赋值
//        nodeTree[n + i].weight = nodeTree[x1].weight + nodeTree[x2].weight;
        //给新生成结点的左右孩子赋值
        nodeTree[n + i].leftChild = x1;
        nodeTree[n + i].rightChild = x2;
    }
}
#pragma mark - 根据哈弗曼树构造哈夫曼编码
void CreatHaffCode(HaffNode haffTree[], int n , Code haffCode[]){
    Code *temp = (Code *)malloc(sizeof(Code));
    if (!temp) {
        return;
    }
    int child, parent;
    //遍历l叶子结点
    for (int i = 0; i < n; i++) {
        //从0开始计数
        temp->start = 0;
        //取得权重
        temp->weight = haffTree[i].weight;
        //设置叶子结点i为孩子结点
        child = i;
        //找到双亲结点
        parent = haffTree[i].parent;
        //循环到根节点，将其左右孩子重新编码
        while (parent != 0) {
            if (haffTree[parent].leftChild == child) {//左孩子则编码为0，右孩子为1
                temp->bit[temp->start] = 0;
            }else{
                temp->bit[temp->start] = 1;
            }
            temp->start++;
            //此时的双亲变为孩子
            child = parent;
            //获取新的双亲结点
            parent = haffTree[child].parent;
        }
        int p = 0;
        for (int j = temp->start - 1; j>=0; j--) {
            p = temp->start - j - 1;
            haffCode[i].bit[p] = temp->bit[j];
        }
        haffCode[i].weight = temp->weight;
        haffCode[i].start = temp->start;
    }
}

数据结构与算法之哈夫曼编码

引入哈夫曼思想

哈夫曼编码是如何思考的

利用哈夫曼编码来对发送信息进行编码

哈夫曼编码分析

哈夫曼编码步骤总结

哈弗曼编码代码实现