数据结构与算法(十三) -- 图在线性表中, 数据元素之间是被串起来的, 仅有线性关系, 每一个数据只有一个前驱跟一个后

一、图的定义

在线性表中, 数据元素之间是被串起来的, 仅有线性关系, 每一个数据只有一个前驱跟一个后继. 在树形结构中, 数据元素之间有着明显的层次关系, 并且每一层上的数据元素可能和下一层中多个元素有关, 但只能和上一层中一个元素有关.

可现实中人与人之间的关系非常复杂, 比如我有许多朋友, 每一个朋友也有许多朋友, 朋友的朋友可能是我的朋友可能也不是. 这就不是一个一对一、一对多的关系. 这种多对多的情况就是图.

图是一种较线性表和树更加复杂的数据结构, 图中任意两个数据元素之间都可能相连.

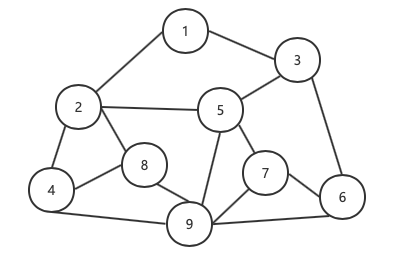
图是由顶点的有穷非空集合和顶点之间边的集合组成, 通常表示为: G(V,E), 其中,G表示一个图, V是图G中顶点的集合, E是图中边的集合.

图的定义:

图中的数据元素, 称之为顶点
图结构中, 不允许没有顶点
在图中, 任意两个顶点之间都可能有关系, 顶点之间的逻辑关系用边来表示, 边集是可以为空的

1.1、各种图定义

1.1.1、无向图

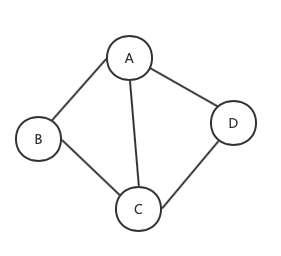
任意一条边的两个顶点之间的连接是没有方向的, 则称这条边为无向边. 如果图中任意两个顶点之间的边都是无向边, 则这个图就称为无向图.

1.1.2、有向图

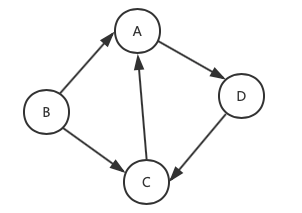
任意一条边的两个顶点之间的连接是有方向的, 则称这条弧为有向边. 如果图中任意两个顶点之间的边都是有向边, 则这个图就称为有向图.

1.1.3、无向完全图

任意两个之间顶点之间都有一条边, 则这个图就称为无向完全图.

1.1.4、有向完全图

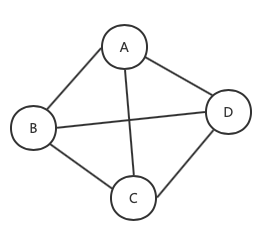
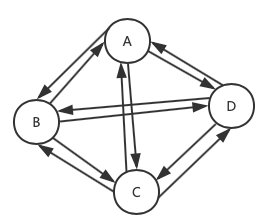
任意两个之间顶点之间都存在方向互为相反的两条边, 则这个图就称为无向完全图.

1.1.5、网

图的边相关的数叫做权, 带权的图通常称之为网.

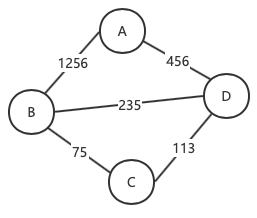
1.1.5、环

第一个顶点到最后一个顶点相同的路径称之为环

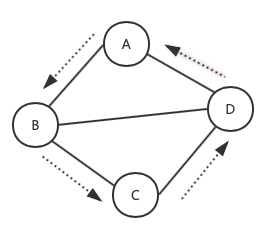
1.1.6、连通图

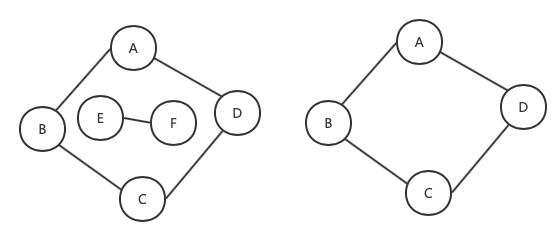
在无向图中, 如果任意两个顶点之间都是连通的, 则称之为联通图 (注: 左:非连通图右:连通图)

二、图的存储

在计算机中, 任何逻辑结构的存储, 最终都会化为顺序存储与链式存储. 这里使用顺序存储来进行图的存储.

2.1、邻接矩阵

考虑到图是由顶点和边或弧组成. 合在一起比较困难, 所以就用两个结构来分别存储. 顶点部分大小主次, 所以用一个一维数组进行存储. 而弧或边是顶点与顶点之间的关系, 就用一个二维数组来存储.

图的邻接存储方式是用两个数组来表示图, 一个用来存储顶点, 一个用二维数组来存储边或弧的信息, 这个二维数据就称为邻接矩阵.

无向图的示例:

f(x)=
\begin{cases}
1& \text{,若(Vi, Vj) 或 <Vi, Vj> ∈ E }\\
0& \text{,反之}
\end{cases}

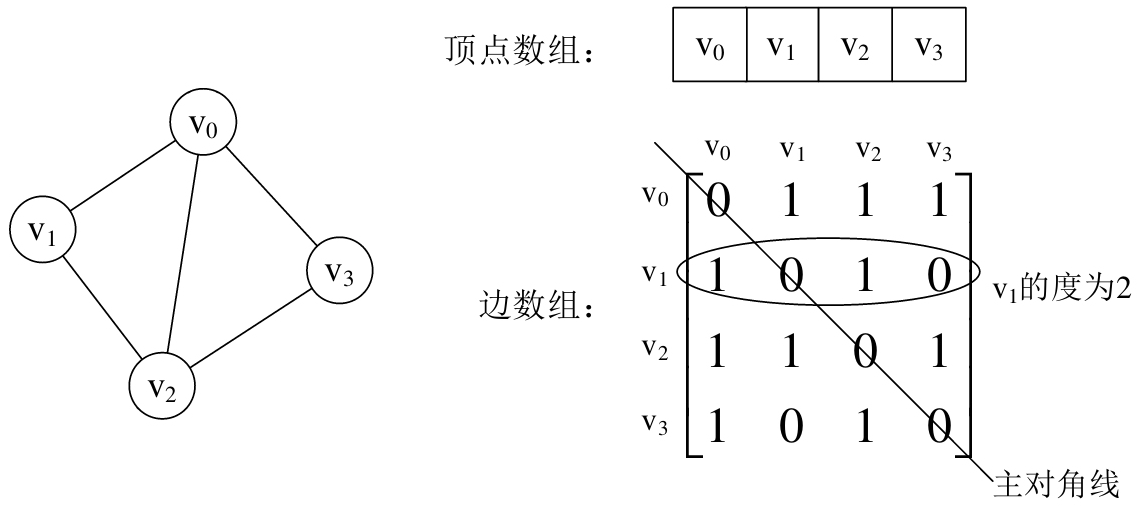
一个顶点Vi与其他顶点的连接关系的和称之为这个顶点的度

当一个图是有向且带权的:

f(x)=
\begin{cases}
w[i]& \text{,若(Vi, Vj) 或 <Vi, Vj> ∈ E }\\
0& \text{, i=j}\\
∞& \text{,反之}\\
\end{cases}

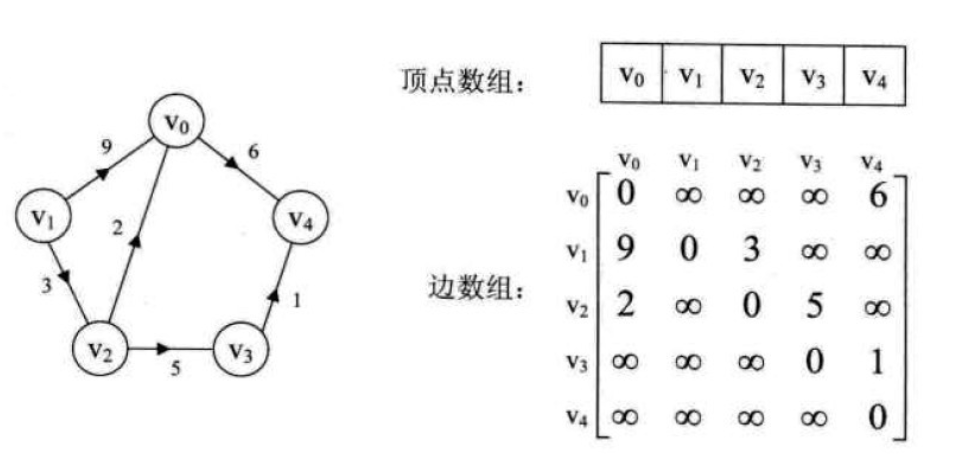
三、代码存储图

#define MAXVEX 100//最大顶点数
#define INFINITY 65535//代替 ∞

typedef char VertexType;//顶点类型
typedef int EdgeType;//权值

typedef struct MGraph {
    VertexType vexs[MAXVEX];//顶点数组
    EdgeType arc[MAXVEX][MAXVEX];//邻接矩阵
    int numNodes;//顶点数
    int numEdges;//边数
    
}MGraph;

3.1、图的邻接矩阵存储

void CreateMGraph(MGraph *G) {
    
    int i, j, k, w;
    //输入顶点数与边数
    printf("输入顶点数和边数:\n");
    scanf("%d,%d", &G->numNodes, &G->numEdges);
    printf("顶点数:%d,边数:%d\n",G->numNodes,G->numEdges);
    
    //输入顶点
    printf("输入顶点信息/顶点表:\n");
    for (i = 0; i < G->numNodes; i++) {
        scanf("%c", &G->vexs[i]);
    }
    
    //初始化邻接矩阵
    for (i = 0; i < G->numNodes; i++) {
        for (j = 0; j < G->numNodes; j++) {
            G->arc[i][j] = INFINITY;
        }
    }
    
    
    //输入边表信息(邻接矩阵)
    for (i = 0; i < G->numEdges; i++) {
        printf("输入边(vi,vj)上的下标i,下标j,权重:\n");
        scanf("%d %d %d", &j, &k, &w);
        G->arc[j][k] = w;
    }
    
    //打印邻接矩阵
    for (i = 0; i < G->numNodes; i++) {
        printf("\n");
        for (j = 0; j < G->numNodes; j++) {
            printf("%d ", G->arc[i][j]);
        }
    }
}

3.2、图的邻接表存储

有了顺序存储, 当然就有链式存储了. 用链式存储来存储图, 就需要使用一个邻接表, 用来表示每一个节点都和谁有关系.

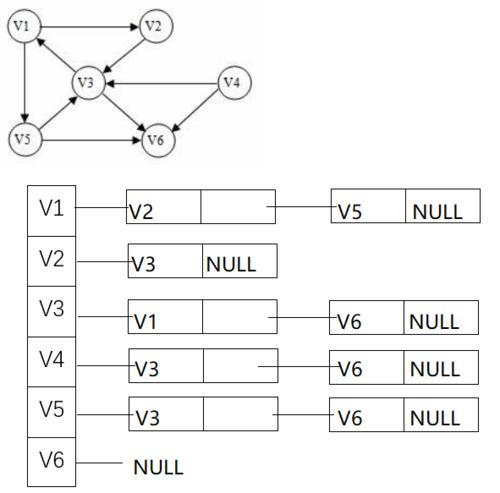
如图, 可以对每一个顶点创建一条关系链表, 每一个顶点与哪些顶点有关都可以记录下来.

定义一个链表, 用来存储每一个顶点与哪些顶点有关

//邻接表的结点
typedef Element int;
typedef struct Node{
    int adj_vex_index;  //弧头的下标，也就是被指向的下标
    Element data;       //权重值
    struct Node * next; //边指针
}EdgeNode;

定义一个顶点结点表, 用来存储每一个顶点, 并且包含一条邻接表结点

//顶点节点表
#define M 100
typedef struct vNode{
    Element data;          //顶点的权值
    EdgeNode * firstedge;  //顶点下一个是谁？
}VertexNode, Adjlist[M];

定一个总图信息结构, 用来存储顶点结点与边数等其他信息:

//总图的一些信息
typedef struct Graph{
    Adjlist adjlist;       //顶点表
    int arc_num;           //边的个数
    int node_num;          //节点个数
    BOOL is_directed;      //是不是有向图
}Graph, *GraphLink;

用链式结构创建一个图:

void creatGraph(GraphLink *g){
    
    int i, j, k;
    EdgeNode *p;
    
    //输入顶点 边 是否有向
    printf("输入顶点数、边数、是否有向:\n");
    scanf("%d,%d,%d", &i, &j, &k);
    (*g)->arc_num = i;
    (*g)->node_num = j;
    (*g)->is_directed = k;

    //顶点表
    printf("输入顶点信息：\n");
    for (i = 0; i < (*g)->node_num; i++) {
        getchar();
        scanf("%c", &(*g)->adjlist[i].data);
        (*g)->adjlist[i].firstedge = NULL;
    }
    
    //边信息
    printf("输入边信息：\n");
    for (k = 0; k < (*g)->arc_num; k++){
        getchar();
        scanf("%d %d", &i, &j);
        
        //新建一个节点
        p = (EdgeNode *)malloc(sizeof(EdgeNode));
        //弧头的下标
        p->adj_vex_index = j;
        //头插法插进去，插的时候要找到弧尾，那就是顶点数组的下标i
        p->next = (*g)->adjlist[i].firstedge;
        //将顶点数组[i].firstedge 设置为p
        (*g)->adjlist[i].firstedge = p;
        
        if(!(*g)->is_directed)
        {
            //新建一个节点
            p = (EdgeNode *)malloc(sizeof(EdgeNode));
            //弧头的下标i
            p->adj_vex_index = i;
            //头插法插进去，插的时候要找到弧尾，那就是顶点数组的下标i
            p->next = (*g)->adjlist[j].firstedge;
            //将顶点数组[i].firstedge 设置为p
            (*g)->adjlist[j].firstedge = p;
        }
    }
}

四、图的遍历

4.1、深度遍历

深度遍历又叫深度优先搜索(DFS: depth first search)

4.1.1、使用邻接矩阵来实现深度遍历

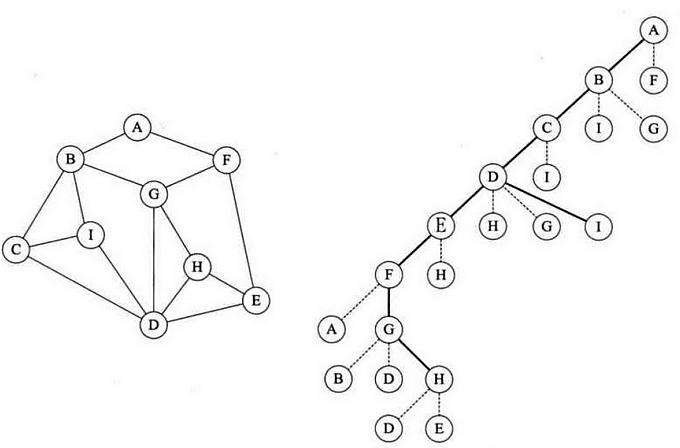
以A为起点, A与B、F相连, 定一个结点A, B、F为A的左右子结点.
依次生成结点来到F, 此时F与A、G有关, 那么为了避免走到重复的结点, 所以我们需要定义一个数组用来标记哪些结点是已经遍历过了的,
所以此时走G. 依次类推, 走到H.
发现H的子结点都走过, 这个时候就需要进行一次回退来到G,
重复 4 步骤来到D结点, 发现I并没有遍历, 此时遍历I
再次利用标记进行查询, 确保所有结点都已经遍历

//深度遍历
//是否遍历过的标记
Boolean visited[MAXVEX];

void DFS(MGraph G, int i) {
    
    visited[i] = true;//遍历过
    printf("%c", G.vexs[i]);
    
    //遍历每一个节点的邻接结点
    for(int j = 0; j < G.numNodes;j++){
        if(G.arc[i][j] == 1 && !visited[j])
            DFS(G, j);
    }
}


void DFSTravese(MGraph G) {
    //标记初始化
    for (int i = 0; i < G.numNodes; i++) {
        visited[i] = false;
    }
    //遍历每一个结点
    for (int i = 0; i < G.numNodes; i++) {
        if (!visited[i]) {
            DFS(G, i);
        }
    }
    
}

4.1.1、使用邻接表来实现深度遍历

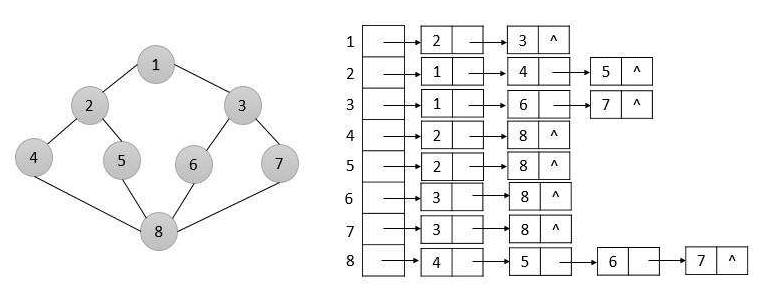
首先从1开始, 下一个为2, 跳往2,
2的下一个为1, 已经遍历, 跳往4
4的下一个为2, 已经遍历, 跳往8
8的下一个为4, 已经遍历, 跳往5
5的下一个为2, 已经遍历, 下一个8, 已经遍历, 直接前往下一个结点6
6的下一个为3, 跳往3
3的下一个为1, 已经遍历, 下一个6, 已经遍历, 跳往7
7的下一个为3, 已经遍历, 下一个8, 已经遍历, 直接前往8, 已经遍历, 遍历完毕
DDF为: 1 2 4 8 5 6 3 7

/* 邻接表的深度优先递归算法 */
void DFS(GraphLink GL, int i)
{
    EdgeNode *p;
    visited[i] = TRUE;
    
    //打印顶点 A
    printf("%c ",GL->adjlist[i].data);
    
    p = GL->adjlist[i].firstedge;
    
    //向下找到没有遍历的结点
    while (p) {
        if(!visited[p->adj_vex_index]) {
            DFS(GL,p->adj_vex_index);
        }
        p = p->next;
    }
    
}
/* 邻接表的深度遍历操作 */
void DFSTraverse(GraphLink GL)
{
    //标记初始化
    for (int i = 0; i < GL->node_num; i++) {
        visited[i] = FALSE;
    }
    //选择一个顶点开始DFS遍历.
    for(int i = 0; i < GL->node_num; i++)
        //对未访问过的顶点调用DFS, 若是连通图则只会执行一次.
        if(!visited[i]) {
            DFS(GL, i);
        }
}

4.2、广度遍历

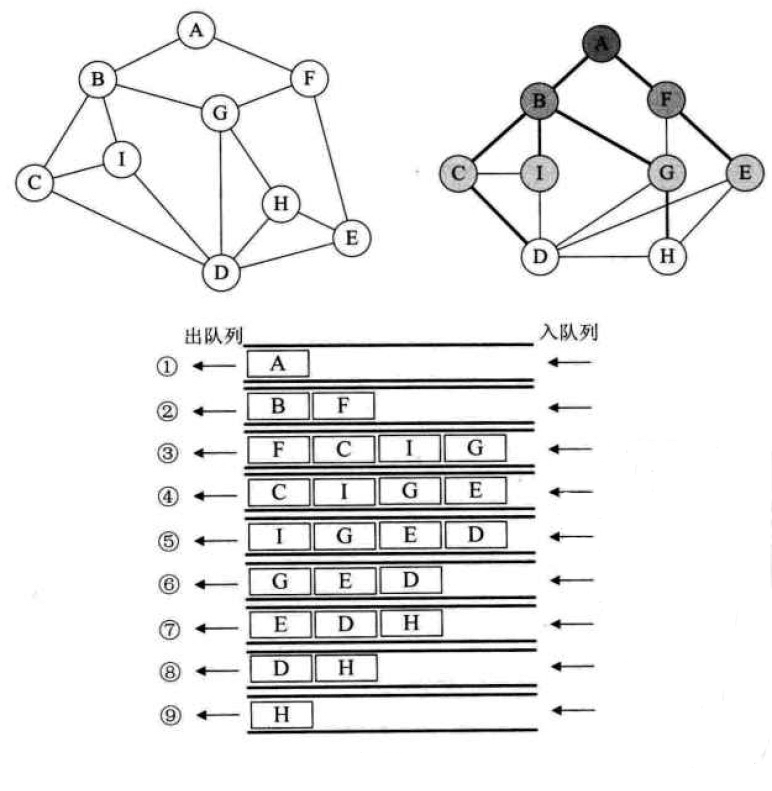
选任意一结点(A)入队列
A出队列, 入A的邻接结点B、F
B出队列, 入B的邻接结点C、I、G
F出队列, 入F的邻接结点E
C出队列, 入C的邻接结点D
I出队列, 入I的邻接结点(均重复, 无)
G出队列, 入G的邻接结点H
E出队列, 入E的邻接结点(均重复, 无)
D出队列, 入D的邻接结点(均重复, 无)
H出队列, 入H的邻接结点(均重复, 无)

4.1.1、使用邻接矩阵来实现广度遍历

Boolean visited[MAXVEX]; /* 访问标志的数组 */
void BFSTraverse(MGraph G){
    
    //创建队列
    Queue Q;
    InitQueue(&Q);//初始化队列
    
    //初始化标记
    for (int i = 0 ; i < G.numNodes; i++) {
        visited[i] = FALSE;
    }
    
    //对遍历邻接表中的每一个顶点(对于连通图只会执行1次,这个循环是针对非连通图)
    for (int i = 0 ; i < G.numNodes; i++) {
        
        if(!visited[i]){
            visited[i] = TRUE;
            printf("%c  ",G.vexs[i]);
            EnQueue(&Q, i);//入队
            while (!QueueEmpty(Q)) {
                DeQueue(&Q, &i);//出队
                for (int j = 0; j < G.numNodes; j++) {
                    if(G.arc[i][j] == 1 && !visited[j])
                    {    visited[j] = TRUE;
                        printf("%c   ",G.vexs[j]);
                        EnQueue(&Q, j);入队
                    }
                }
            }
        }
        
    }
}

4.1.2、使用邻接表来实现广度遍历

void BFS2Traverse(GraphLink GL){
    
    //创建结点
    EdgeNode *p;
    //创建队列
    Queue Q;
    InitQueue(&Q);//初始化队列
    
    //初始化标记
    for(int i = 0; i < GL->node_num; i++)
        visited[i] = FALSE;
    
    //对遍历邻接表中的每一个顶点(对于连通图只会执行1次,这个循环是针对非连通图)
    for(int i = 0 ;i < GL->node_num;i++){
        //判断当前结点是否被访问过.
        if(!visited[i]){
            visited[i] = TRUE;
            //打印顶点
            printf("%c ",GL->adjlist[i].data);
            
            EnQueue(&Q, i);//入队
            while (!QueueEmpty(Q)) {
                DeQueue(&Q, &i);//出队
                p = GL->adjlist[i].firstedge;
                while (p) {
                    //判断
                    if(!visited[p->adj_vex_index]){
                        visited[p->adj_vex_index] = TRUE;
                        printf("%c ",GL->adjlist[p->adj_vex_index].data);
                        EnQueue(&Q, p->adj_vex_index);//入队
                    }
                    p = p->next;
                }
            }
            
        }
    }
}