前言
本文写作目的旨在巩固自己的基础知识,记录学习感悟,集中资源帮助读者快速上手代码。本文参考了浙大MOOC何钦铭老师对堆的讲解。
1.堆(heap)
堆是具有特殊性质的完全二叉树,每个结点的值大于等于其左右孩子的堆称为大顶堆(MaxHeap);每个结点的值小于等于其左右孩子的堆称为小顶堆(MinHeap)。
2.运行环境
- 编辑器:Atom + 插件
linter-gcc与linter与gcc-make-run - 简单配置步骤:
- 下载并安装MinGW,配置好环境变量bin,include和lib
- 做科学家,在Atom上安装上述三个插件
linter-gcc-setting将路径改为gcc- 写完代码后按F6编译运行
3.堆类型的定义
typedef struct HeapStruct *MaxHeap; //定义指针
struct HeapStruct {
int *Elements; //存储堆元素的数组
int Size;
int Capacity; //堆的最大容量
};
这里定义指针*Elements便于我们在创建堆的时候动态分配数组,Size代表堆当前保存的有效元素,Capacity代表堆最多可以保存的元素数目。
3.建造一个大顶堆(MaxHeap)
这里抽象成三个函数。
Create()函数负责堆的初始化,注意前两句的用法,先申请结点空间,再去动态分配数组空间。MaxSize+1的原因是我们规定堆的有效元素从Elements数组下标1处开始存储,而Elements[0]作为哨兵保存一个最大的数据MaxData(与保存的值无关,需要我们自己设定,插入元素时可以用到)。- 第二个函数
PercDown()用来每次将一个指定结点调到合适的位置,使以当前的结点为根的子堆符合大顶堆的性质。具体步骤如下:
- 先取出指定的结点
Elements[p]存入临时变量X中,使用Parent指针遍历当前子树的左孩子,如果右孩子存在,且右孩子值大于左孩子值,就让Child指向右孩子,该指针始终指向每层孩子中的值最大的孩子。 - 如果
X>Elements[Child]即父亲比孩子的值大,那么符合大顶堆性质,便不再改动。 - 如果父亲比孩子的值小,把孩子的值(也就是Elements[Child])拷贝给父亲(也就是Elements[Parent]),此时结束这一层的循环,开始下一层子孙的循环。
- 循环结束后,
Parent指针一定会走到合适的位置,此时把之前保存的值放到该位置即可。
BuildHeap()函数,负责建造堆,在这里录入数据,通过参数设定堆的有效元素个数。这里需要我们理解堆的创建过程:我们每次的PercDown()都是排列堆。我们选择最后一个结点的父结点,是因为该节点仅有一个左孩子,可以看做一个堆,没有右孩子,相当于空堆,我们对两个堆和一个元素在根结点的情形进行排列,这样最终会形成一个新子堆;我们对以当前层结点为根的子堆进行调整调整,不断形成子堆,然后不断向上,最终形成祖先根节点和两个子堆进行调整。至此调整结束。
MaxHeap Create (int MaxSize) {
MaxHeap H = malloc( sizeof(struct HeapStruct) );
H->Elements = malloc( (MaxSize + 1) * sizeof(int) );//申请数组空间
H->Size = 0;
H->Capacity = MaxSize;
//定义哨兵为大于堆中所有可能的值,便于插入时不必设置循环遍历i>1
//堆元素从下标1开始存放
H->Elements[0] = MaxData;
return H;
}
void PercDown( MaxHeap H, int p )
{ /* 下滤:将H中以H->Elements[p]为根的子堆调整为最大堆 */
int Parent, Child;
int X;
X = H->Elements[p]; /* 取出根结点存放的值 */
for( Parent = p; Parent * 2 <= H->Size; Parent = Child ) {
Child = Parent * 2; //取左孩子
if( (Child != H->Size) && ( H->Elements[Child] < H->Elements[Child+1]) )
Child++; /* Child指向左右子结点的较大者 */
if( X >= H->Elements[Child] ) break; /* 找到了合适位置 */
else /* 下滤X */
H->Elements[Parent] = H->Elements[Child];
}
H->Elements[Parent] = X;
}
void BuildHeap( MaxHeap H, int Size)
{ /* 调整H->Elements[]中的元素,使满足最大堆的有序性 */
int i;
for (i = 1; i <= Size; i++)
scanf("%d",&(H->Elements[i]));
H->Size = Size;
/* 从最后一个结点的父节点开始,到根结点1 */
for( i = H->Size / 2; i>0; i-- )
PercDown( H, i );
}
4.堆的其他操作
4.1 元素插入堆
先判断堆是否满,再将新元素插入到堆的末尾。此时我们遍历末尾结点的父结点A,如果父结点A值较小,就把父结点值赋给末尾结点,然后再看父结点A的父结点B,以此类推,直到不满足父亲值小于孩子值的条件或者走到下标0为止。
void Insert (MaxHeap H, int item) {
int i;
if (H->Size == H->Capacity) {
printf("The Heap is full!\n");
return;
}
i = ++H->Size;
for (; H->Elements[i/2] < item; i/=2) {//如果没有设置哨兵,需要条件i>1
H->Elements[i] = H->Elements[i/2]; //把父亲的值赋给孩子,小元素下沉
}
H->Elements[i] = item;
}
4.2 删除堆顶
先判断堆是否为空,非空则取走堆顶的值。然后将最后一个元素作为祖先根元素保存起来,之后进行堆的调整。调整过程与之前类似,暂略。
//从大顶堆中取出最大元素,并删除一个结点
int DeleteMax(MaxHeap H) {
int Parent, Child;
int MaxItem, temp;
if(H->Size == 0) {
printf("The Heap is Empty!\n");
return 0;
}
//取出树根——最大值元素
MaxItem = H->Elements[1];
//用大顶堆中最后一个元素从根节点开始过滤下层结点
temp = H->Elements[H->Size--];
for (Parent = 1; Parent * 2 <= H->Size; Parent = Child) { //是否有左儿子
//从左右儿子中找一个大的
Child = Parent * 2;
if ( (Child != H->Size)&&
(H->Elements[Child] < H->Elements[Child + 1]) ) //有右儿子的情况下 左右儿子比较
Child ++; //Child指向左右子结点的较大者
if ( temp >= H->Elements[Child]) break;//如果比左右儿子较大者还要大,就无需移动位置
else //移动temp元素到下一层
H->Elements[Parent] = H->Elements[Child]; //如果比左右儿子较大者小,那么把大元素拷到双亲位置
}
//此时的位置Parent是副本,放入末尾的元素到合适的位置
H->Elements[Parent] = temp;
return MaxItem;
}
5. 测试
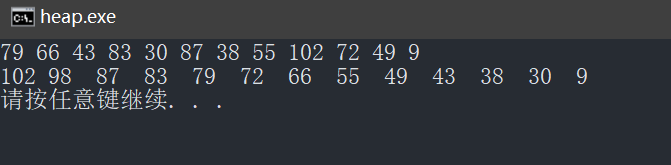
测试数据: 79 66 43 83 30 87 38 55 102 72 49 9
插入数据: 98
int main(int argc, char const *argv[]) {
MaxHeap mh;
mh = Create(20);
BuildHeap(mh,12);
Insert(mh, 98);
int i;
for (i = 1; i < 14; i++)
printf("%-4d", DeleteMax(mh));
printf("\n");
return 0;
}
测试结果:
6. 总结
本文写作用时1.5h,记录了堆的学习过程,但还有不足。目前对于堆排序的写法还没有搞懂,Insert()函数的哨兵作用不熟。需要一些不错的画图工具制作对原理性知识进行解读的图片。希望后面晚上都可以拿出一个小时时间对重点知识进行复盘。
本文使用 mdnice 排版