数据结构-图

DragonetZ
346 阅读11分钟

前言

今天学习另一种非线性结构-图

图结构

逻辑结构中，图结构是一种非线性结构。结构中的结点关系是多对多的关系。如图：

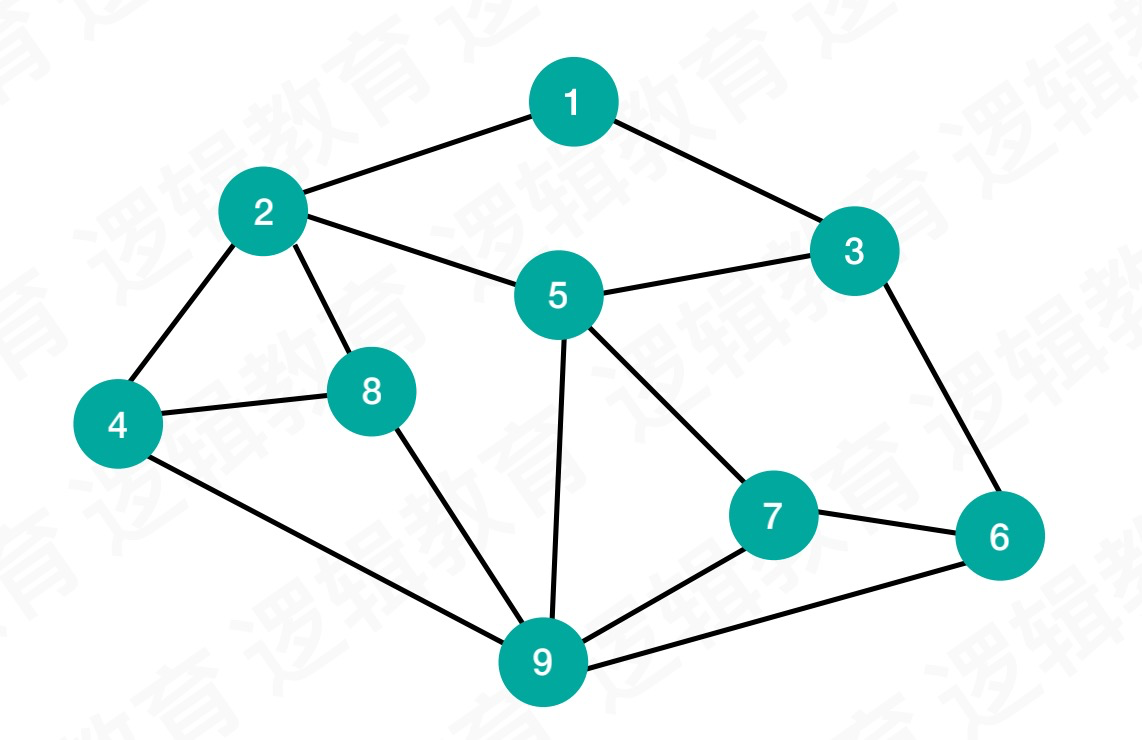
图(Graph) 是由顶点的有穷⾮空集合和顶点之间边的集合组成。 通常表示为: G(V,E)。其中，G表示⼀个图，V是图G中的顶点集合，E是图G中边的集合。

p.s.图结构不像其他数据结构那样，有“空”概念。例如：表可以是空表，树可以是空树。但是图没有空图概念。

图的相关概念和图的类型

通常我们称图中的点为顶点。树中我们称为结点。链表中我们称之为元素。而且图中没有明确的起始顶点，可以用任意的顶点作为起始点。

无向图和有向图

图可分为两种类型，1.无向图 2.有向图

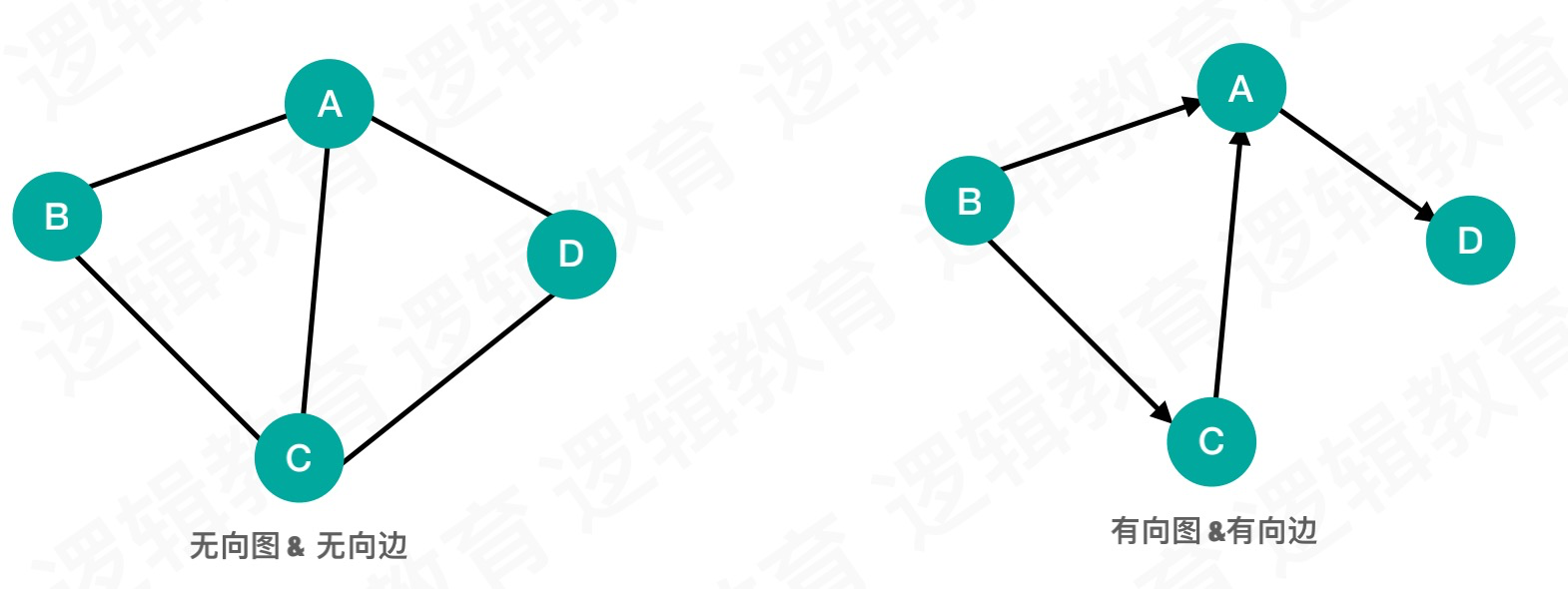
p.s. 所谓的有向和无向都是针对图中的边的定义，所以也可以把无向图称为无向边图和有向边图

完全图

图中任意两个顶点都有边存在的情况，我们称之为完全图，如图：

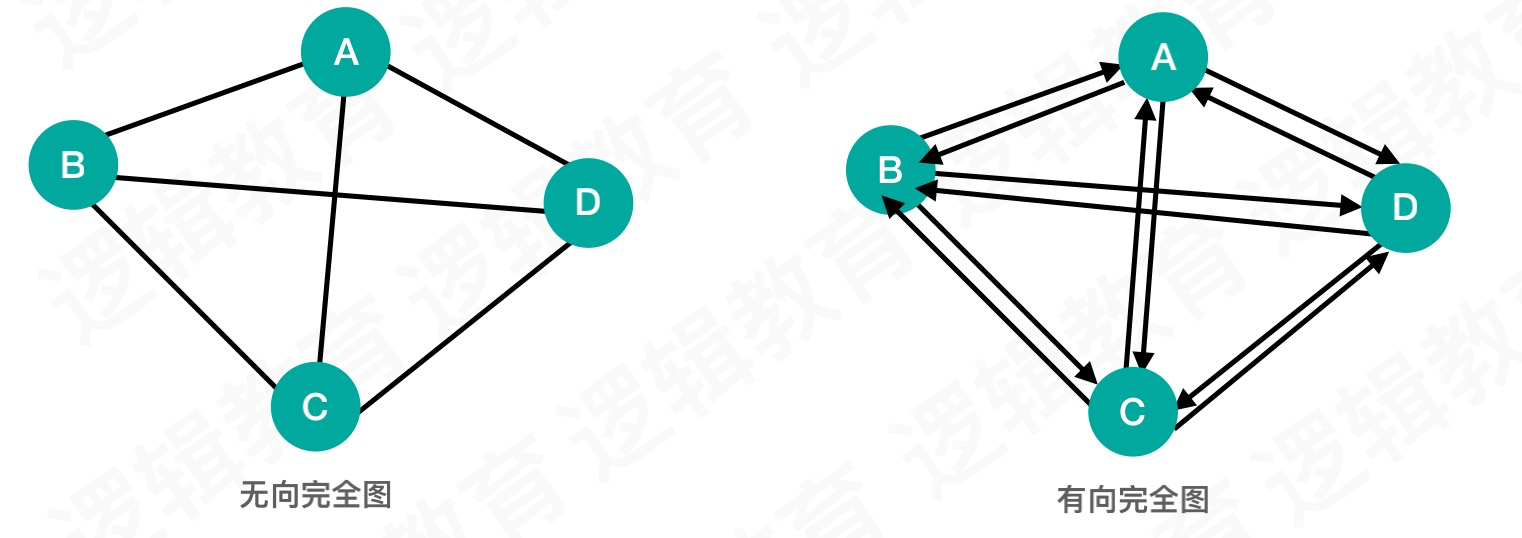
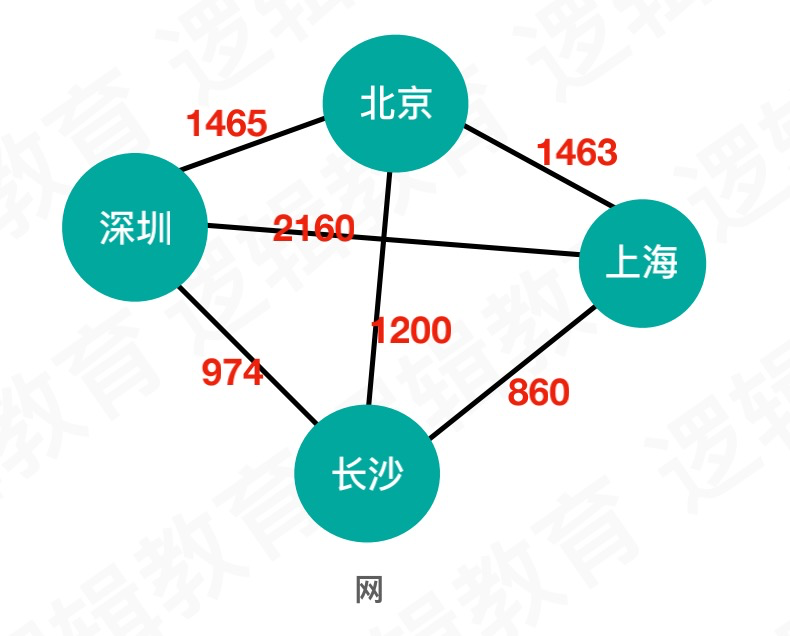
网

图中的边附加上权重，我们通常称之为：网

子图

这个概念和树中的子树差不多，也很好理解：

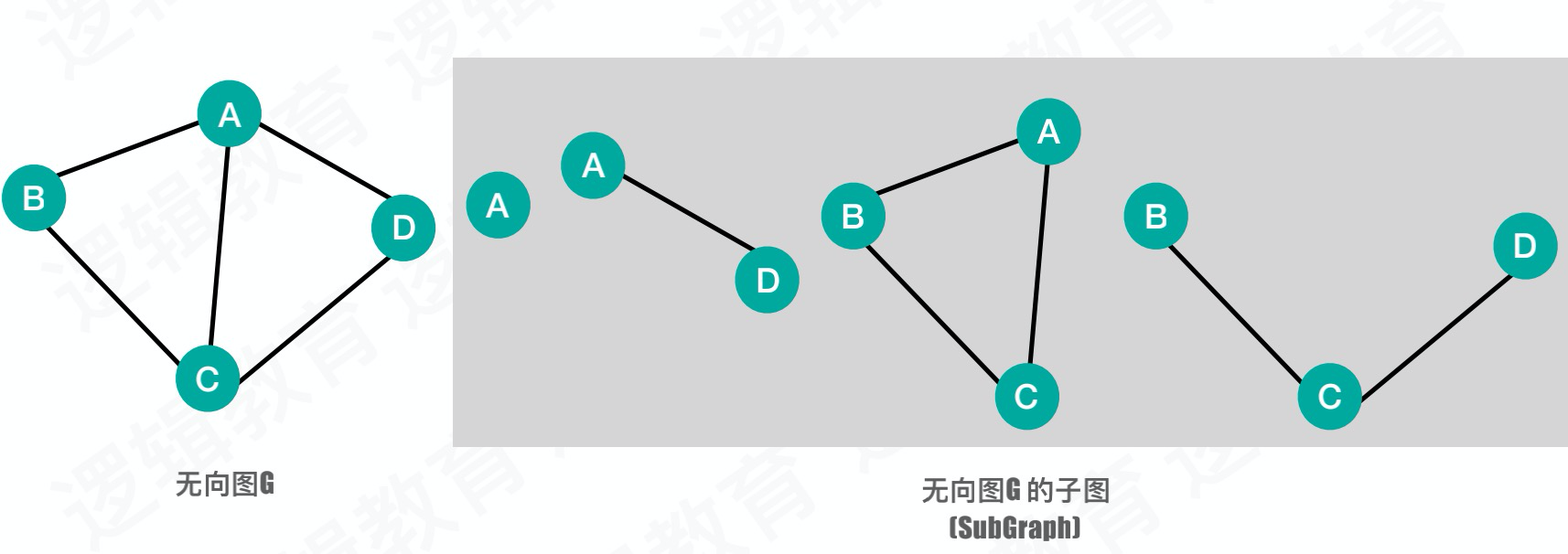
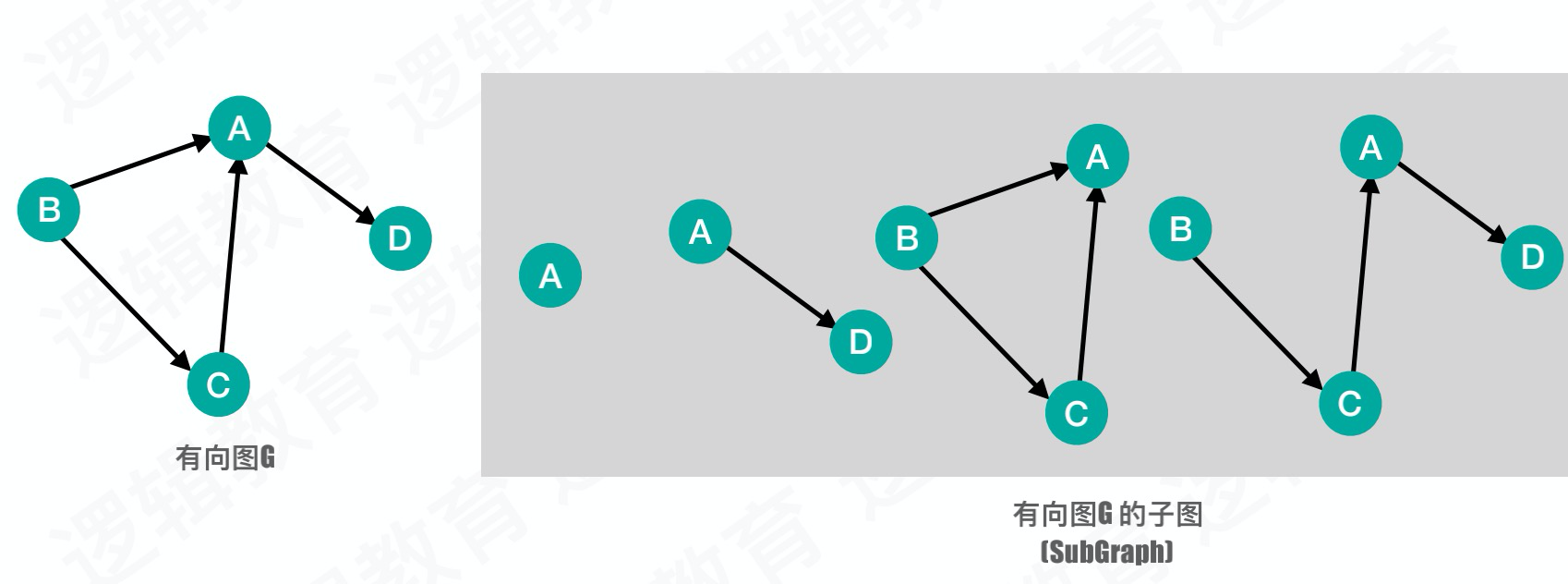
图的存储

在物理存储中，分为顺序和链式两种存储方式。图的存储也是一样，只是叫法稍有不同，分别为邻接矩阵方式（顺序存储）和邻接表的方式（链式存储）。这两种说法其实主要是针对于边的存储而定义的。

邻接矩阵

用一个简单的一维数组表示顶点信息，用矩阵也就是二维数组来记录边的信息。用简单的无向图例子说明一下：

图中的顶点数组：{v0,v1,v2,v3}

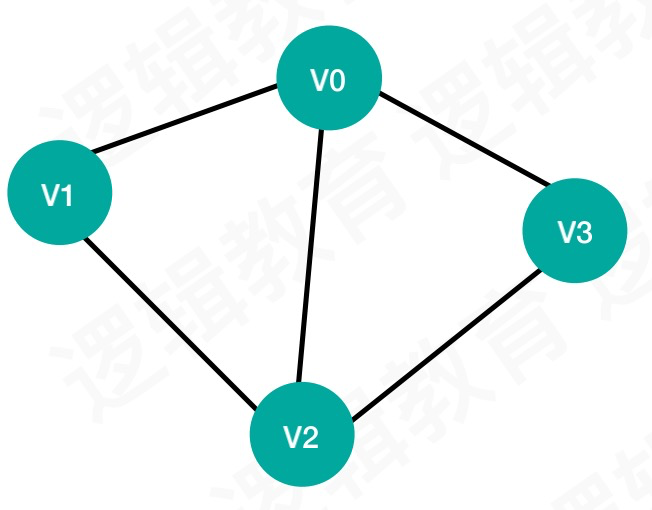
边二维数组：

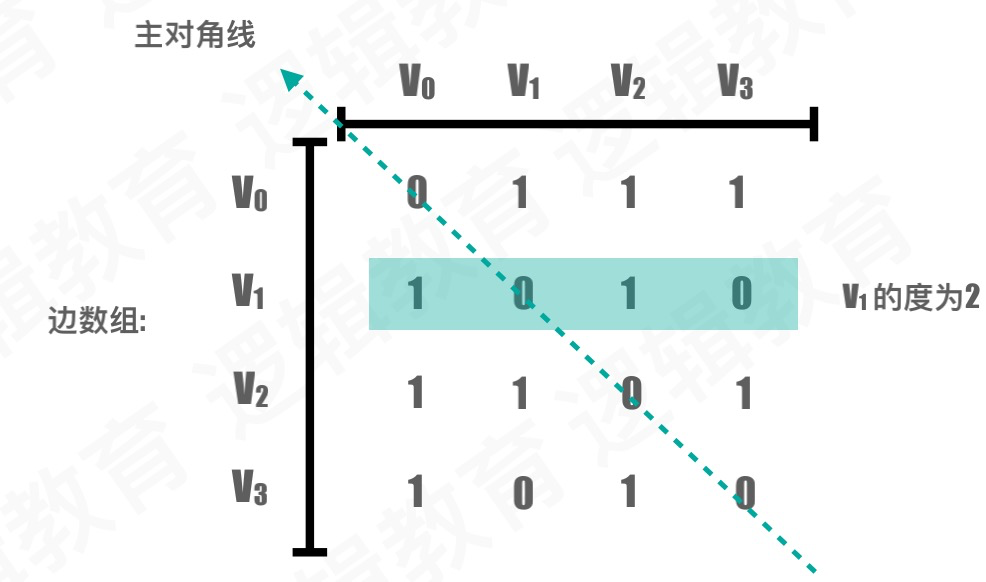
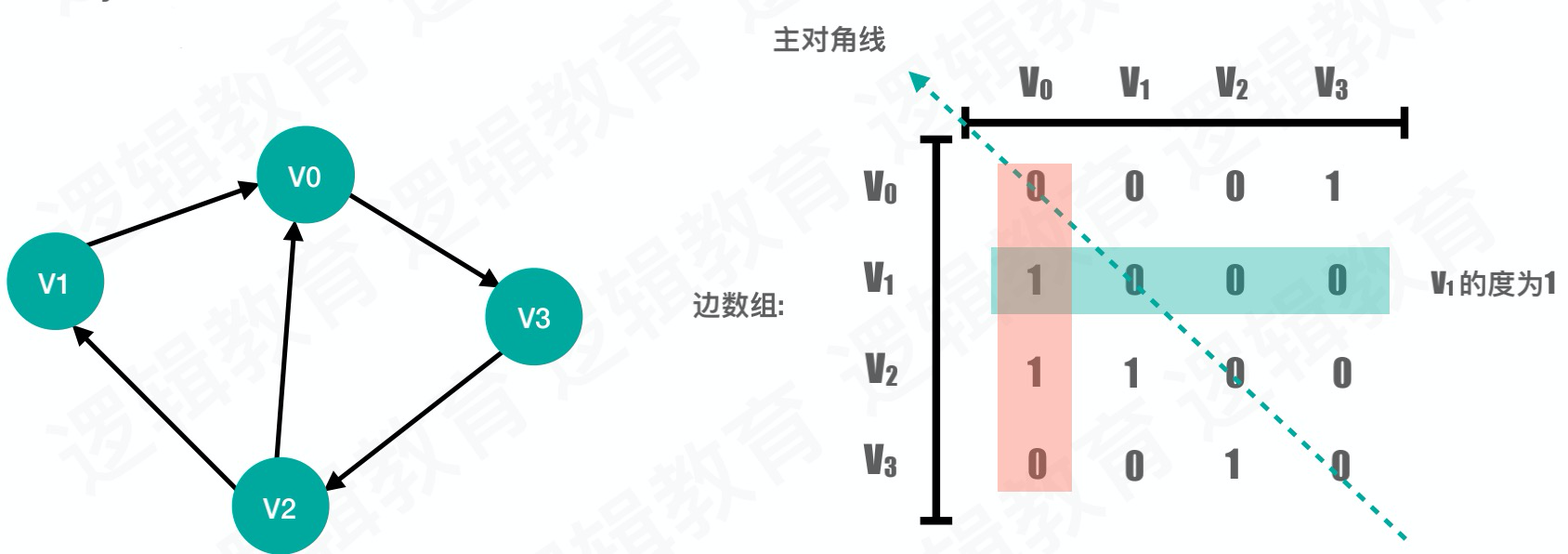
无向图中，边的方向可以理解为是双向的，所以边二维数组是以对角线对称的。有向图中则不是对称关系，如图：

邻接矩阵数据结构定义
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXVEX 100 /* 最大顶点数，应由用户定义 */
#define INFINITYC 0

typedef int Status;
typedef char VertexType;
typedef int EdgeType;
typedef struct Graph{
    VertexType vertex[MAXVEX];
    EdgeType edge[MAXVEX][MAXVEX];
    int numVertex, numEdge;
}Graph;
代码实现
  1. 确定顶点数和边数
  2. 读取顶点信息
  3. 初始化邻接矩阵
  4. 读入边信息
  5. 循环打印
void createGraph(Graph *graph) {
    printf("输入顶点数和边数:\n");
    scanf("%d,%d", &graph->numVertex, &graph->numEdge);
    printf("顶点数:%d,边数:%d\n",graph->numVertex,graph->numEdge);
    
    //清除之前输入的缓冲区
    fflush(stdin);
    
    //输入顶点信息，初始化顶点表
    for (int i = 0; i< graph->numVertex; i++) {
        scanf("%c",&graph->vertex[i]);
    }
    
    //打印顶点数组
    for (int i = 0; i < graph->numVertex; i++) {
        printf("%c ", graph->vertex[i]);
    }
    printf("\n");
    
    //初始化邻接矩阵
    for (int i = 0; i < graph->numVertex; i++) {
        for (int j = 0; j < graph->numVertex; j++) {
            graph->edge[i][j] = INFINITY;
        }
    }
    
    //输入边表信息
    for (int i = 0; i < graph->numEdge; i++) {
        printf("输入边起始点，终止点，权值\n");
        int j, k, w;
        scanf("%d,%d,%d",&j,&k,&w);

        graph->edge[j][k] = w;
        //无向图，矩阵对称
        graph->edge[k][j] = graph->edge[j][k];
    }
    
    //打印邻接矩阵
    for (int i = 0; i < graph->numVertex; i++) {
        printf("\n");
        for (int j = 0; j < graph->numVertex; j++) {
            printf("%d ", graph->edge[i][j]);
        }
    }
    printf("\n");
}
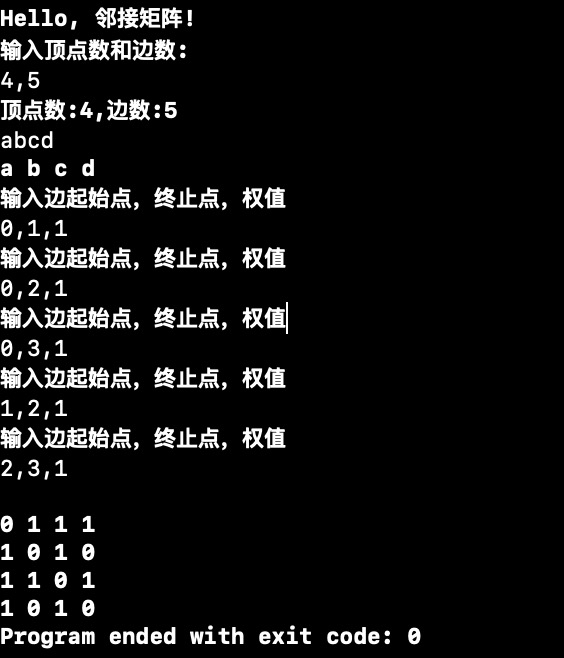
运行
int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, 邻接矩阵!\n");
    
    Graph graph;
    createGraph(&graph);
    
    return 0;
}

邻接表

与邻接矩阵不同点在于记录边信息使用数组+链表的方式记录，

无向图：

有向图：

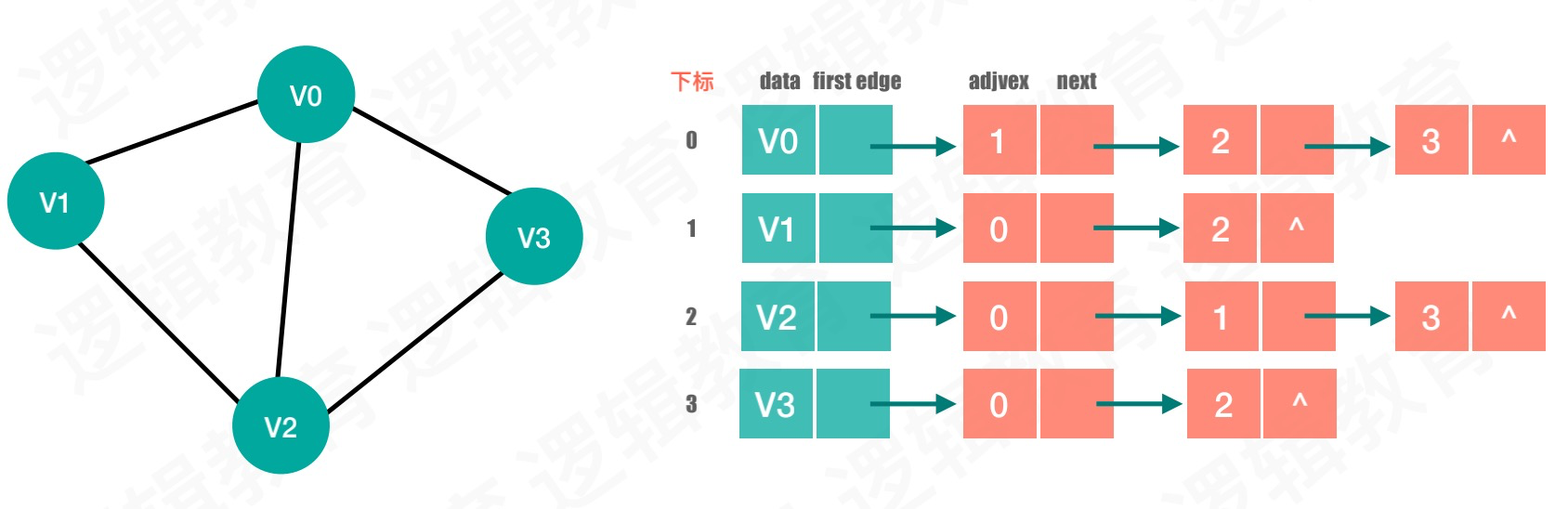
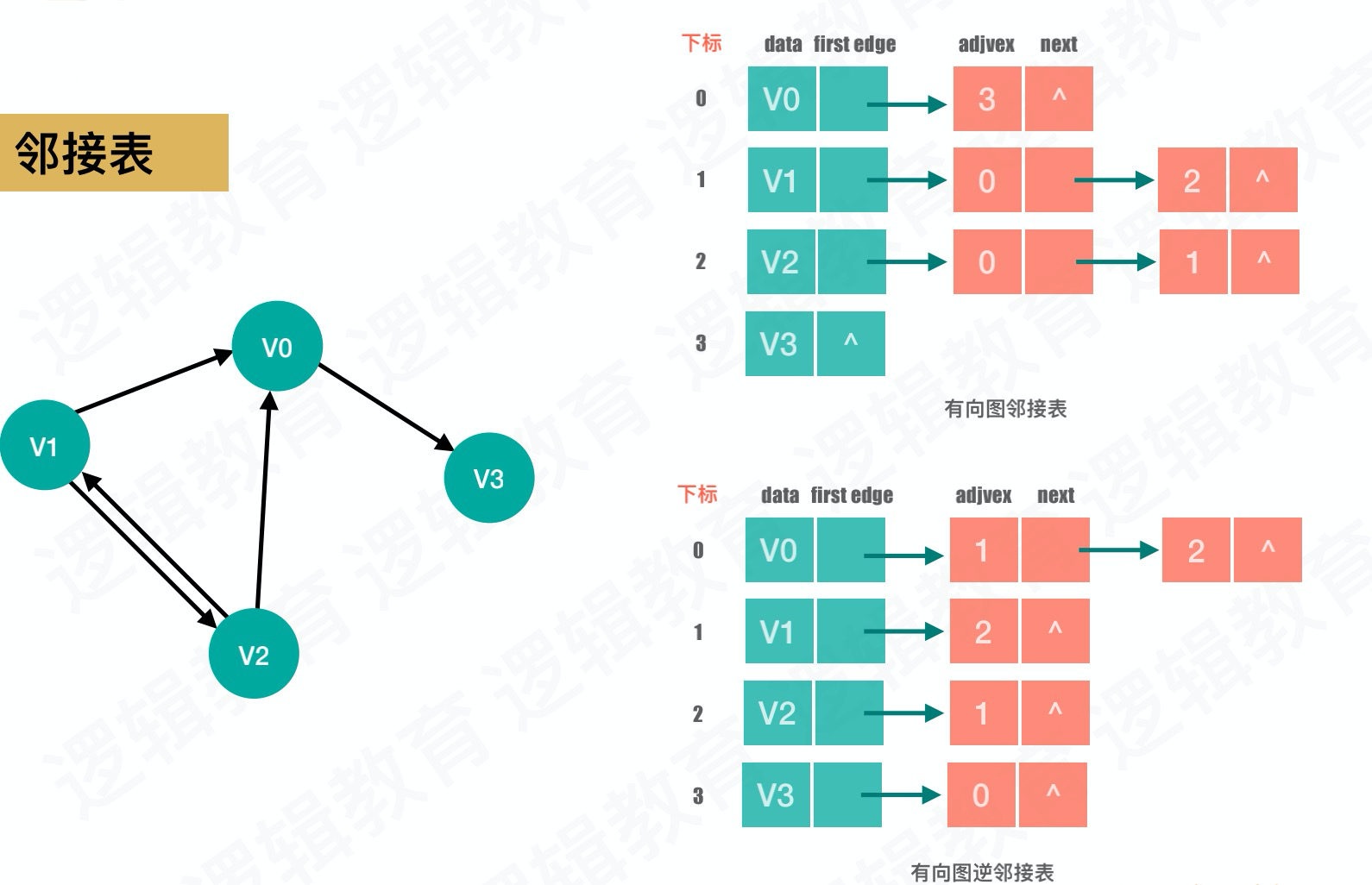
邻接矩阵数据结构定义
#define MAXSIZE 100
#define TRUE 1
#define FALSE 0

typedef char ElemType;
typedef int Weight;
typedef int BOOL;

//邻接表结点
typedef struct Edge{
    int index;
    Weight w;
    struct Edge *next;
}EdgeNode;

//顶点表结点
typedef struct Vertex{
    ElemType data;
    EdgeNode *edgeInfo;
}VertexNode, VertexList[MAXSIZE];

//图
typedef struct Graph {
    VertexList verList;
    int numVertex;//顶点数量
    int numEdge;//边数量
    BOOL isDirected;//是不是有向图 1：有向 0：无向
}Graph, *GraphLink;
代码实现
  1. 确定顶点数和边数
  2. 读取顶点信息
  3. 创建一个结点，插入到对应的顶点数组中
    • 创建边结点p
    • 结点p的index赋值j
    • 将结点p插入到对应的顶点数组的下标i中
    • 将顶点数组[i]的edgeInfo设置为p
void createGraph(GraphLink *g) {
    printf("输入顶点数，边数和是否有向：\n");
    scanf("%d %d %d", &(*g)->numVertex, &(*g)->numEdge, &(*g)->isDirected);
    
    printf("输入顶点信息：\n");
    for (int i = 0; i < (*g)->numVertex; i++) {
        getchar();
        scanf("%c", &(*g)->verList[i].data);
        (*g)->verList[i].edgeInfo = NULL;
    }
    
    printf("输入边信息：\n");
    for (int i = 0; i < (*g)->numEdge; i++) {
        getchar();
        int j, k;
        scanf("%d %d", &j, &k);
        
        EdgeNode * p = (EdgeNode*)malloc(sizeof(EdgeNode));
        p->index = k;
        p->next = (*g)->verList[j].edgeInfo;
        (*g)->verList[j].edgeInfo = p;
        
        //不是有向
        if (!(*g)->isDirected) {
            p = (EdgeNode*)malloc(sizeof(EdgeNode));
            p->index = j;
            p->next = (*g)->verList[k].edgeInfo;
            (*g)->verList[k].edgeInfo = p;
        }
    }
}

void putGraph(GraphLink g) {
    printf("邻接表中存储的信息：\n");
    for (int i = 0; i < g->numVertex; i++) {
        EdgeNode *p = g->verList[i].edgeInfo;
        while (p) {
            printf("%c->%c ", g->verList[i].data, g->verList[p->index].data);
            p = p->next;
        }
        printf("\n");
    }
}
运行
int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, 图-邻接表!\n");
    
//    输入顶点数，边数和是否有向：
//    4 5 0
//    输入顶点信息：
//    0 1 2 3
//    输入边信息：
//    0 3 0 2 0 1 2 1 2 3
//    邻接表中存储的信息：
//    0->1 0->2 0->3
//    1->2 1->0
//    2->3 2->1 2->0
//    3->2 3->0
    
//    输入顶点数，边数和是否有向：
//    4 5 1
//    输入顶点信息：
//    0 1 2 3
//    输入边信息：
//    1 0 1 2 2 0 2 1 0 3
//    邻接表中存储的信息：
//    0->3
//    1->2 1->0
//    2->1 2->0
    
    GraphLink g = (GraphLink)malloc(sizeof(Graph));
    createGraph(&g);
    putGraph(g);
    
    return 0;
}

图的遍历

分为两种：深度优先遍历和广度优先遍历，以下相关代码和解释都以这张图的结构为例：

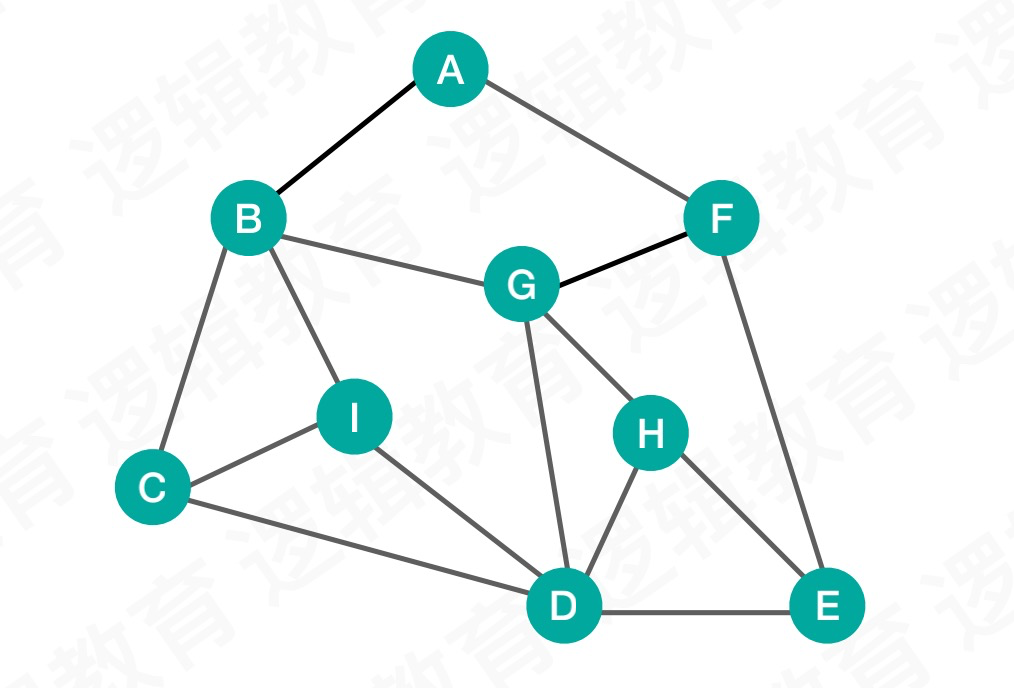
深度优先遍历

思路：

  1. 以任意顶点开始出发，遍历查找与这个当前顶点有关联的所有顶点中的最右侧的顶点（右侧为相对位置的右侧）。例如当前顶点A，与他有关联的顶点有B、F，而A的相对位置右侧是顶点B（比如你站在A点上，B点就是右侧的点）。
  2. 当某个顶点被访问过了，就标记为“以访问”状态。根据这个逻辑，遍历整张图。
  3. 当遍历到某一个顶点时，没有“未访问”过的关联顶点。我们需要按照之前的路径开始回退。回退过程找找是否存在“未访问”的结点。
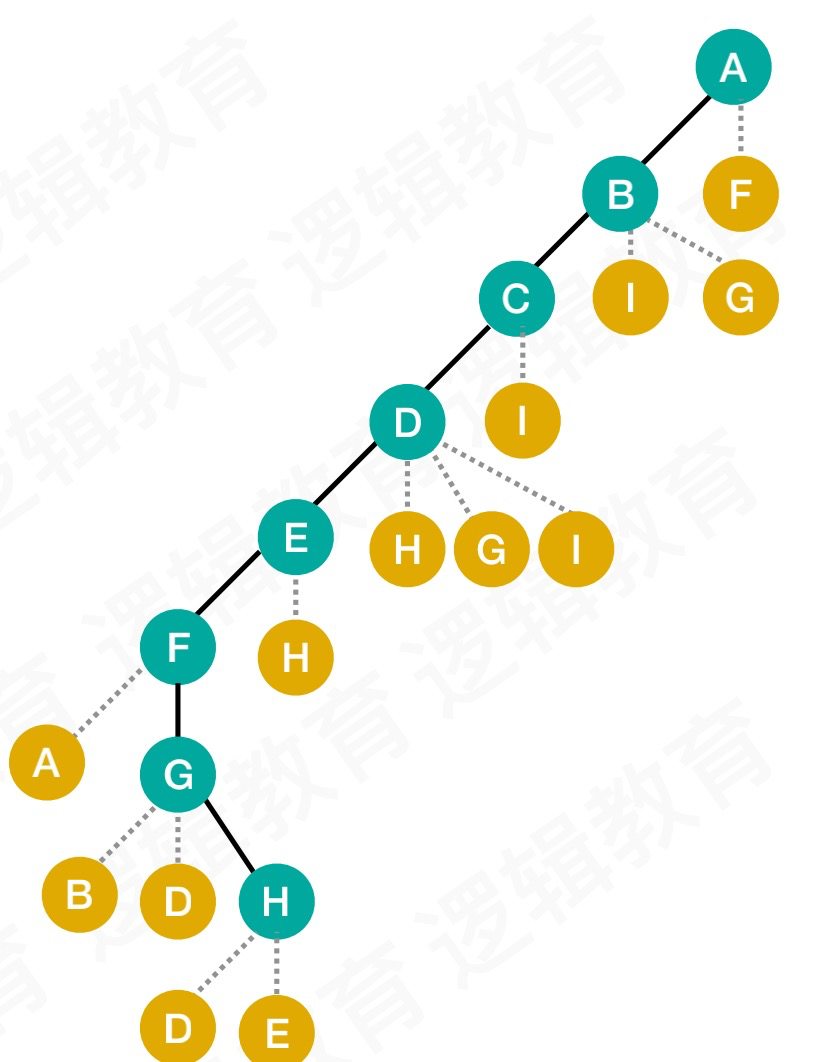
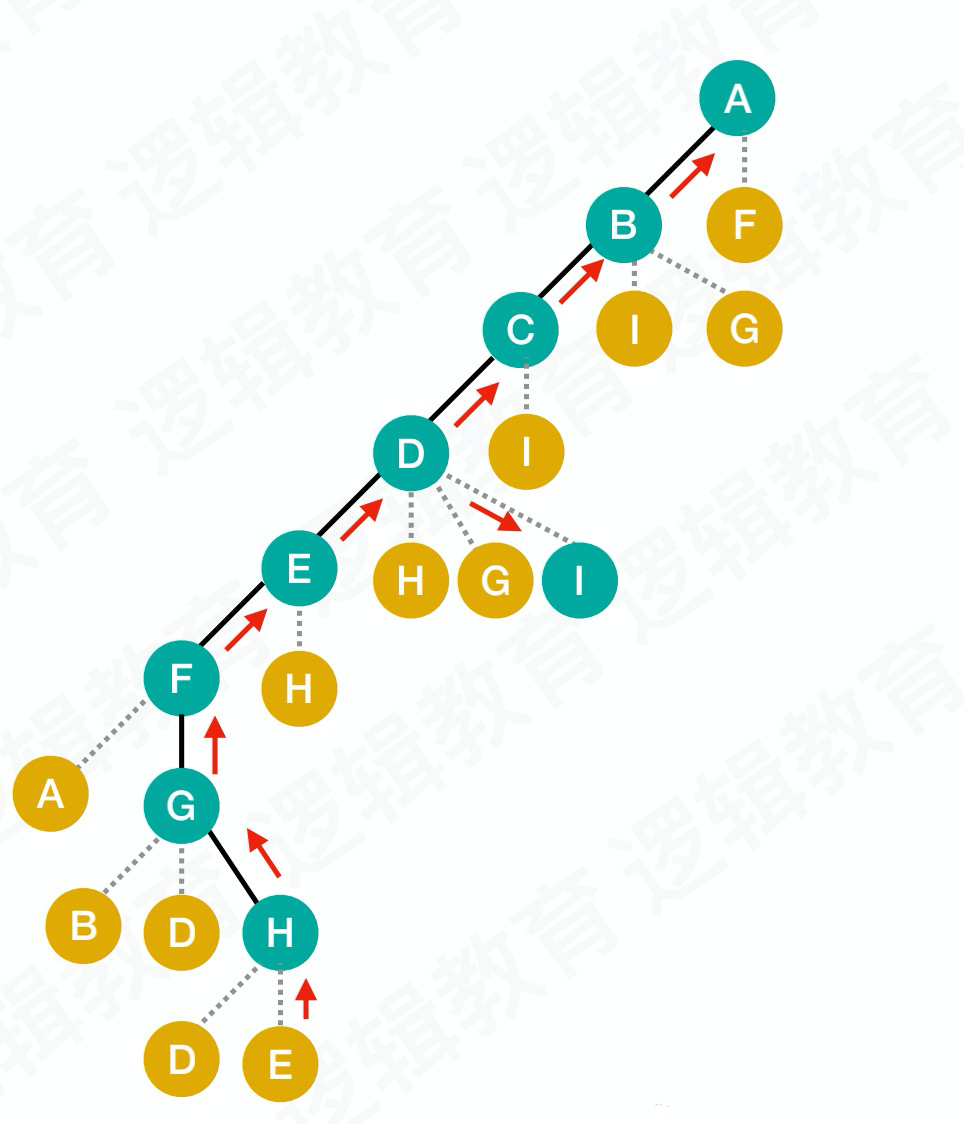
    图中绿色结点为遍历路径，其实我们会发现没有访问到I顶点，所以我们要根据绿色路径进行回退操作，来找到I顶点

代码实现

相关的数据结构，可以参考上面的代码

初始化图

用邻接矩阵的方式初始化图

void createGraph(Graph *g) {
    //初始顶点数和边数
    g->numVertex = 9;
    g->numArc = 15;
    
    //创建顶点表
    g->vertex[0] = 'A';
    g->vertex[1] = 'B';
    g->vertex[2] = 'C';
    g->vertex[3] = 'D';
    g->vertex[4] = 'E';
    g->vertex[5] = 'F';
    g->vertex[6] = 'G';
    g->vertex[7] = 'H';
    g->vertex[8] = 'I';
    
    //初始化边表
    for (int i = 0; i < g->numVertex; i++) {
        for (int j = 0; j < g->numVertex; j++) {
            g->arc[i][j] = 0;
        }
    }
    
    //设置邻接矩阵
    //A-B, A-F
    g->arc[0][1] = 1;
    g->arc[0][5] = 1;
    //B-C,B-G,B-I
    g->arc[1][2] = 1;
    g->arc[1][6] = 1;
    g->arc[1][8] = 1;
    //C->D I
    g->arc[2][3] = 1;
    g->arc[2][8] = 1;
    //D->E G H I
    g->arc[3][4] = 1;
    g->arc[3][6] = 1;
    g->arc[3][7] = 1;
    g->arc[3][8] = 1;
    //E->F H
    g->arc[4][5] = 1;
    g->arc[4][7] = 1;
    //F->G
    g->arc[5][6] = 1;
    //H->G
    g->arc[6][7] = 1;
    
    //无向图对称处理
    for (int i = 0; i < g->numVertex; i++) {
        for (int j = 0; j < g->numVertex; j++) {
            g->arc[i][j] = g->arc[j][i];
        }
    }
}
邻接矩阵的方式深度优先遍历
//结点是否已经访问过
BOOL visited[MAX_VERTEX];
void DFS(Graph g, int i) {
    visited[i] = TRUE;
    printf("%c", g.vertex[i]);
    
    for (int j = 0; j < g.numVertex; j++) {
        if (g.arc[i][j] == 1 && !visited[j]) {
            DFS(g, j);
        }
    }
}

void DFSTravese(Graph g) {
    for (int i = 0; i < g.numVertex; i++) {
        visited[i] = FALSE;
    }
    
    for (int i = 0; i < g.numVertex; i++) {
        if (!visited[i]) {
            DFS(g, i);
        }
    }
}

int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, 邻接矩阵深度优先遍历!\n");
    Graph g;
    createGraph(&g);
    DFSTravese(g);
    printf("\n");
    return 0;
}
邻接表的方式深度优先遍历

使用邻接矩阵初始化的图转换成邻接表的方式

//创建邻接表结构的图
void createLGraph(MGraph mg, GraphLink *lg) {
    *lg = (GraphLink)malloc(sizeof(LGraph));
    //从mg中获取顶点数和边数
    (*lg)->numVertex = mg.numVertex;
    (*lg)->numEdge = mg.numArc;
    
    //从mg中获取顶点信息
    for (int i = 0; i < mg.numVertex; i++) {
        (*lg)->verList[i].data = mg.vertex[i];
        (*lg)->verList[i].edgeInfo = NULL;
    }
    
    for (int i = 0; i < mg.numVertex; i++) {
        for (int j = 0; j < mg.numVertex; j++) {
            if (mg.arc[i][j] == 1) {
                EdgeNode *e = (EdgeNode*)malloc(sizeof(EdgeNode));
                e->index = j;
                e->next = (*lg)->verList[i].edgeInfo;
                (*lg)->verList[i].edgeInfo = e;
            }
        }
    }
}


//结点是否已经访问过的标记数组
BOOL visited[MAX_VERTEX];
void DFS(GraphLink lg, int i) {
    visited[i] = TRUE;
    printf("%c ", lg->verList[i].data);
    EdgeNode *p = lg->verList[i].edgeInfo;
    
    while (p) {
        if (!visited[p->index]) {
            DFS(lg, p->index);
        }
        p = p->next;
    }
}

void DFSTraverse(GraphLink lg) {
    for (int i = 0; i < lg->numVertex; i++) {
        visited[i] = FALSE;
    }
    
    for (int i = 0; i < lg->numVertex; i++) {
        if (!visited[i]) {
            DFS(lg, i);
        }
    }
}

int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, 邻接表深度优先遍历!\n");
    
    MGraph g;
    createGraph(&g);
    GraphLink lg;
    createLGraph(g, &lg);
    
    DFSTraverse(lg);
    printf("\n");
    
    return 0;
}

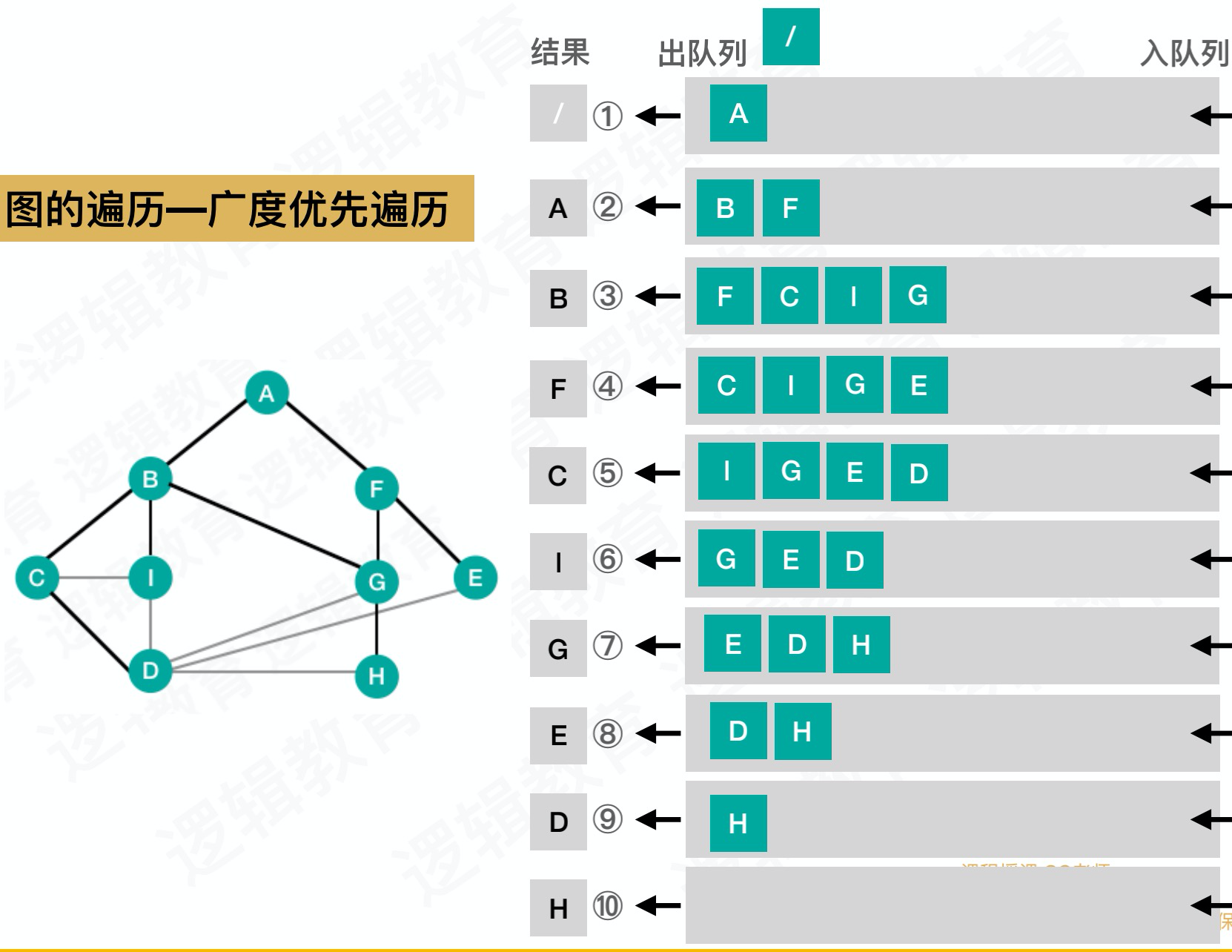
广度优先遍历

有点类似于书的层遍历，可以将例子中的图稍微进行一点点形变：

思路：利用队列来实现

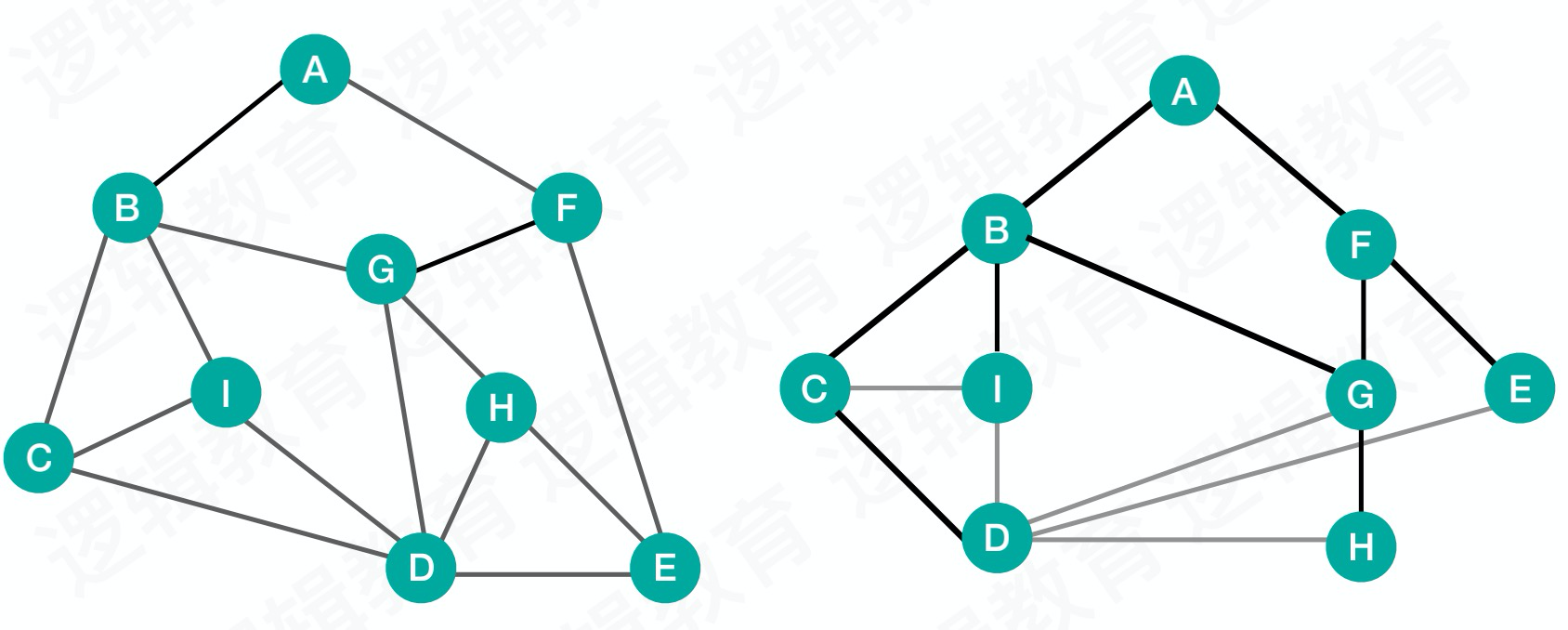
  1. 把根结点入队
  2. 出队一个结点，该结点标记为“已访问”，把这个结点所有的相关联的结点并且是“未访问”状态的结点入队。
  3. 找到所有要找到元素时结束。

代码实现

队列相关操作
/* 循环队列的顺序存储结构 */
typedef struct
{
    int data[MAXSIZE];
    int front;        /* 头指针 */
    int rear;        /* 尾指针，若队列不空，指向队列尾元素的下一个位置 */
}Queue;

/* 初始化一个空队列Q */
Status InitQueue(Queue *Q)
{
    Q->front=0;
    Q->rear=0;
    return  OK;
}

/* 若队列Q为空队列,则返回TRUE,否则返回FALSE */
Status QueueEmpty(Queue Q)
{
    if(Q.front==Q.rear) /* 队列空的标志 */
    return TRUE;
    else
    return FALSE;
}

/* 若队列未满，则插入元素e为Q新的队尾元素 */
Status EnQueue(Queue *Q,int e)
{
    if ((Q->rear+1)%MAXSIZE == Q->front)    /* 队列满的判断 */
    return ERROR;
    Q->data[Q->rear]=e;            /* 将元素e赋值给队尾 */
    Q->rear=(Q->rear+1)%MAXSIZE;/* rear指针向后移一位置， */
    /* 若到最后则转到数组头部 */
    return  OK;
}

/* 若队列不空，则删除Q中队头元素，用e返回其值 */
Status DeQueue(Queue *Q,int *e)
{
    if (Q->front == Q->rear)            /* 队列空的判断 */
    return ERROR;
    *e=Q->data[Q->front];                /* 将队头元素赋值给e */
    Q->front=(Q->front+1)%MAXSIZE;    /* front指针向后移一位置， */
    /* 若到最后则转到数组头部 */
    return  OK;
}
邻接矩阵的方式深度优先遍历
BOOL visited[MAX_VERTEX]; /* 访问标志的数组 */
void BFSTraverse(Graph G){
    Queue Q;
    InitQueue(&Q);
    
    for (int i = 0; i < G.numVertex; i++) {
        visited[i] = FALSE;
    }
    
    for (int i = 0; i < G.numVertex; i++) {
        if (!visited[i]) {
            visited[i] = TRUE;
            printf("%c ", G.vertex[i]);
            
            EnQueue(&Q, i);
            while (!QueueEmpty(Q)) {
                DeQueue(&Q, &i);
                for (int j = 0; j < G.numVertex; j++) {
                    if (G.arc[i][j] == 1 && !visited[j]) {
                        visited[j] = TRUE;
                        printf("%c ", G.vertex[j]);
                        EnQueue(&Q, j);
                    }
                }
            }
        }
    }
}

int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, 邻接矩阵广度优先遍历!\n");
    
    Graph g;
    createGraph(&g);
    BFSTraverse(g);
    printf("\n");
    
    return 0;
}
邻接表的方式深度优先遍历
//创建邻接表结构的图
void createLGraph(MGraph mg, GraphLink *lg) {
    *lg = (GraphLink)malloc(sizeof(LGraph));
    //从mg中获取顶点数和边数
    (*lg)->numVertex = mg.numVertex;
    (*lg)->numEdge = mg.numArc;
    
    //从mg中获取顶点信息
    for (int i = 0; i < mg.numVertex; i++) {
        (*lg)->verList[i].data = mg.vertex[i];
        (*lg)->verList[i].edgeInfo = NULL;
    }
    
    for (int i = 0; i < mg.numVertex; i++) {
        for (int j = 0; j < mg.numVertex; j++) {
            if (mg.arc[i][j] == 1) {
                EdgeNode *e = (EdgeNode*)malloc(sizeof(EdgeNode));
                e->index = j;
                e->next = (*lg)->verList[i].edgeInfo;
                (*lg)->verList[i].edgeInfo = e;
            }
        }
    }
}

BOOL visited[MAX_VERTEX];
void BFSTraverse(GraphLink gl) {
    Queue Q;
    InitQueue(&Q);
    
    for (int i = 0; i < gl->numVertex; i++) {
        visited[i] = FALSE;
    }
    
    for (int i = 0; i < gl->numVertex; i++) {
        if (!visited[i]) {
            visited[i] = TRUE;
            printf("%c ", gl->verList[i].data);
            
            EnQueue(&Q, i);
            while (!QueueEmpty(Q)) {
                DeQueue(&Q, &i);
                EdgeNode *p = gl->verList[i].edgeInfo;
                while (p) {
                    if (!visited[p->index]) {
                        visited[p->index] = TRUE;
                        printf("%c ", gl->verList[p->index].data);
                        EnQueue(&Q, p->index);
                    }
                    p = p->next;
                }
            }
        }
    }
}

int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, 邻接表广度优先遍历!\n");
    
    MGraph G;
    createGraph(&G);
    GraphLink GL;
    createLGraph(G, &GL);
    
    BFSTraverse(GL);
    printf("\n");
    
    return 0;
}
avatar
文章
阅读
粉丝