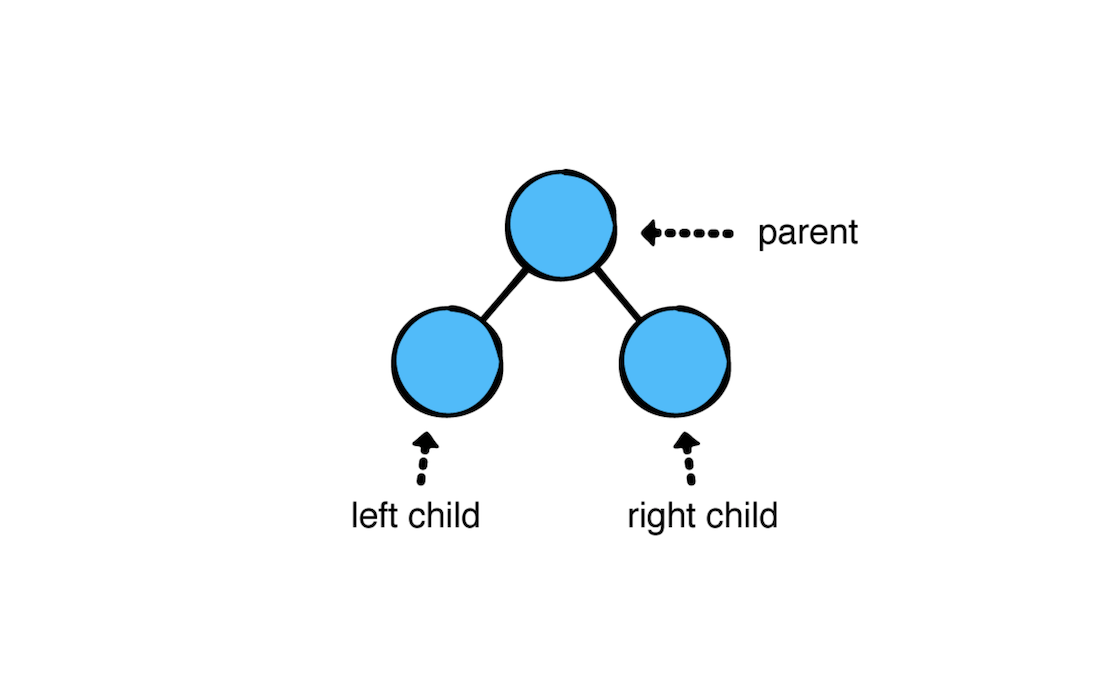
树型数据结构 - 二叉树如图所示，一个二叉树的父节点最多只有两个子节点。二叉树是很多树型数据结构和很多算法的基础。在本文

如图所示，一个二叉树的父节点最多只有两个子节点。二叉树是很多树型数据结构和很多算法的基础。在本文中主要是看一下二叉树三种不同的遍历方式。

实现

下面是基本代码：

class BinaryNode<Element> {
    
    var value: Element
    var leftChild: BinaryNode?
    var rightChild: BinaryNode?

    init(value: Element) {
        self.value = value
    }
}

里面的内容很简单。一个当前节点的数据，一个左节点（可选），一个右节点（可选）。

添加一个测试数据：

var tree: BinaryNode<Int> = {
    let zero = BinaryNode(value: 0)
    let one = BinaryNode(value: 1)
    let five = BinaryNode(value: 5)
    let seven = BinaryNode(value: 7)
    let eight = BinaryNode(value: 8)
    let nine = BinaryNode(value: 9)
    
    seven.leftChild = one
    one.leftChild = zero
    one.rightChild = five
    seven.rightChild = nine
    nine.leftChild = eight
    
    return seven
}()

它返回的是这样一个二叉树：

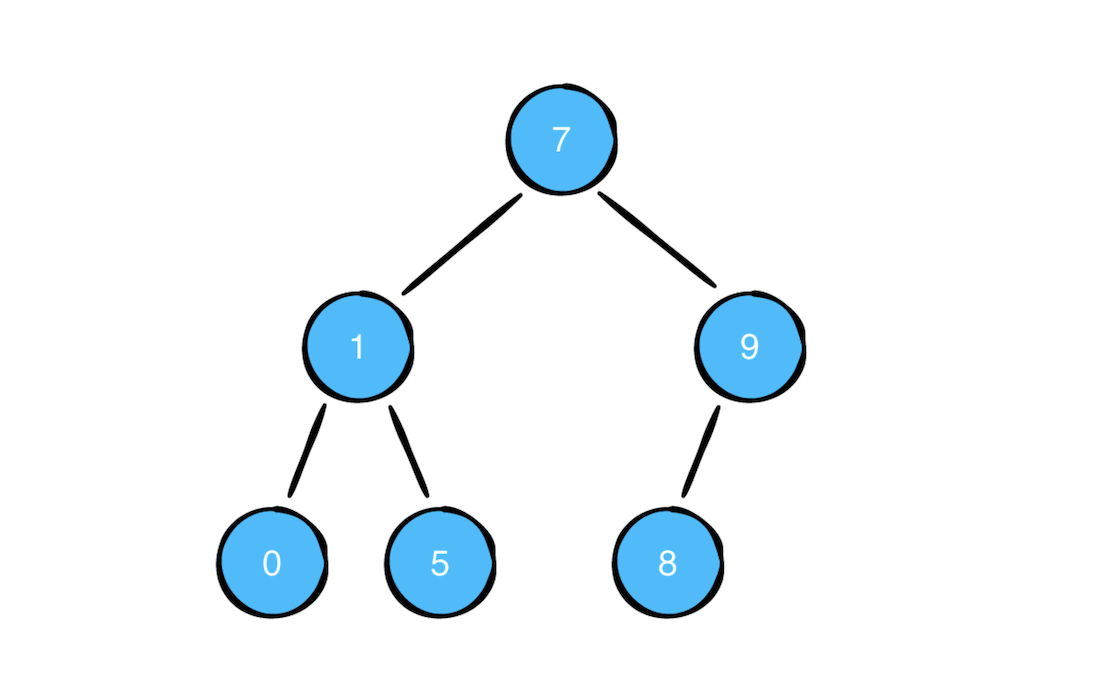
图像化输出

为了在测试中更好的查看二叉树的输出结构，下面我们添加一个图像化的输出：

extension BinaryNode: CustomStringConvertible {
    
    public var description: String {
        diagram(for: self)
    }
    
    private func diagram(for node: BinaryNode?,
                         _ top: String = "",
                         _ root: String = "",
                         _ bottom: String = "") -> String {
        guard let node = node else {
            return root + "nil\n"
        }
        if node.leftChild == nil && node.rightChild == nil {
            return root + "\(node.value)\n"
        }
        return diagram(for: node.rightChild,
                       top + " ", top + "┌──", top + "│ ")
            + root + "\(node.value)\n"
            + diagram(for: node.leftChild,
                      bottom + "│ ", bottom + "└──", bottom + " ")
    }
}

具体的实现算法可以在这查看： www.objc.io/books/optim…

再添加一个辅助：

public func example(of description: String, action: () -> Void) {
    print("---Example of: \(description)---")
    action()
    print()
}

测试：

example(of: "tree diagram") {
    print(tree)
}

输出：

---Example of: tree diagram---
 ┌──nil
┌──9
│ └──8
7
│ ┌──5
└──1
 └──0

现在查看二叉树的结构图就很直观了。

遍历算法

下面会介绍三种不同的遍历方式。

中序遍历

遍历规则：

如果当前节点有左节点，先循环处理左节点
处理自己节点
如果当前节点有右节点，先循环处理右节点

其实遍历顺序就是【左节点 -> 自己 -> 右节点】。遍历图如下所示：

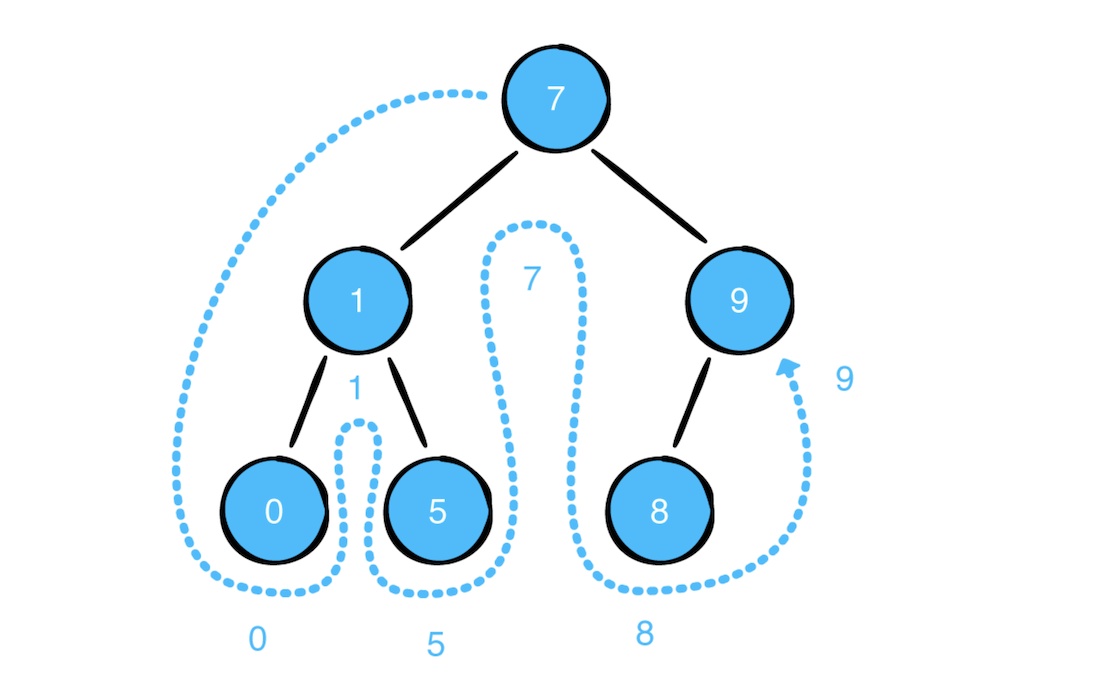
其实在图中可看出这是一个升序遍历，在二叉搜索树会看到更多的 中序遍历 内容。

添加代码实现：

extension BinaryNode {
    func traverseInOrder(visit: (Element) -> Void) {
        leftChild?.traverseInOrder(visit: visit)
        visit(value)
        rightChild?.traverseInOrder(visit: visit)
    }
}

测试：

example(of: "in-order traversal") {
    tree.traverseInOrder { print($0) }
}

输出：

---Example of: in-order traversal---
0
1
5
7
8
9

前序遍历

遍历规则：【自己 -> 左节点 -> 右节点】。遍历图如下所示：

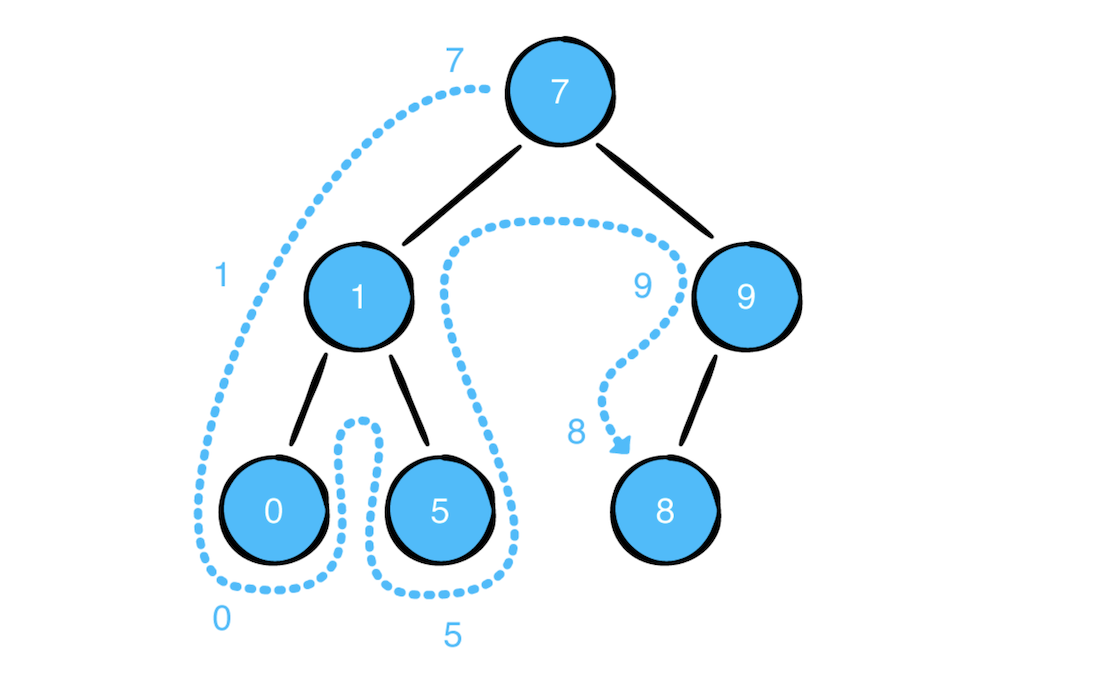
添加代码实现：

extension BinaryNode {
    func traversePreOrder(visit: (Element) -> Void) {
        visit(value)
        leftChild?.traversePreOrder(visit: visit)
        rightChild?.traversePreOrder(visit: visit)
    }
}

测试：

example(of: "pre-order traversal") {
    tree.traversePreOrder { print($0) }
}

输出：

---Example of: pre-order traversal---
7
1
0
5
9
8

后序遍历

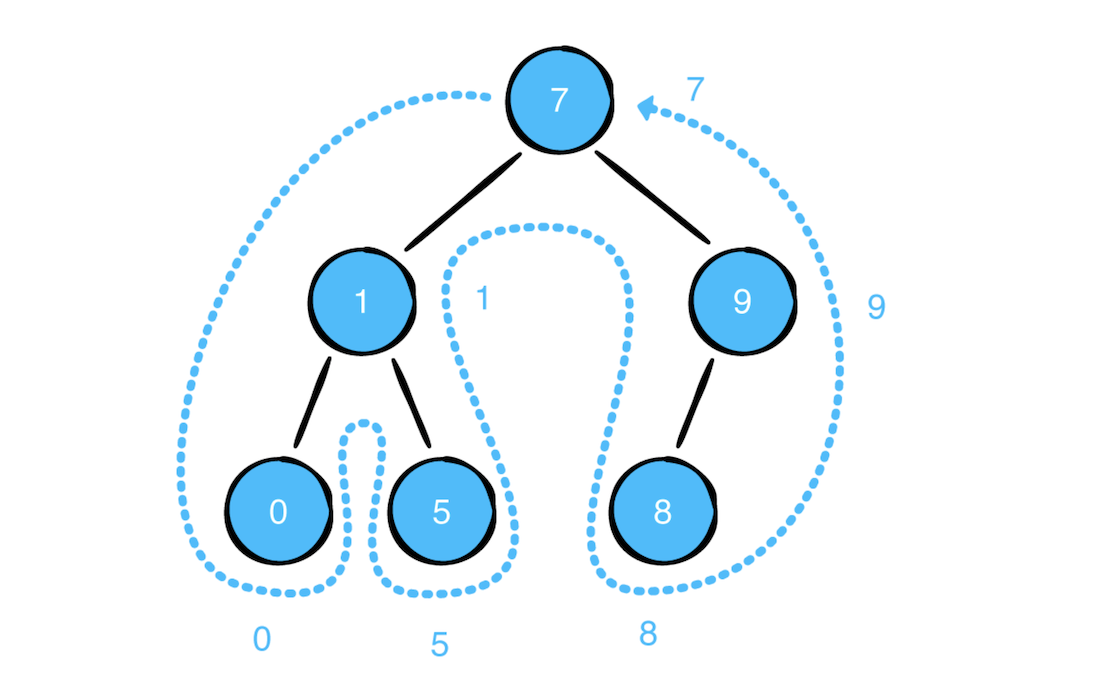
遍历规则：【左节点 -> 右节点 -> 自己】。遍历图如下所示：

添加代码实现：

extension BinaryNode {
    func traversePostOrder(visit: (Element) -> Void) {
        leftChild?.traversePostOrder(visit: visit)
        rightChild?.traversePostOrder(visit: visit)
        visit(value)
    }
}

测试：

example(of: "post-order traversal") {
    tree.traversePostOrder { print($0) }
}

输出：

---Example of: post-order traversal---
0
5
1
8
9
7

上面的三种遍历算法其实都很简单，它们的核心思想还是递归，不断的递归遍历数据。它们的时间复杂度和空间复杂度都是 O(n)

要点
二叉树是很多树型数据结构的基础，比如 二叉搜索树 和 AVL树 就是在二叉树的基础上做的一些扩展。
上面的三种遍历方式其实可以适用于很多的树型数据结构。
试题

求二叉树的高度（如果只有一个节点，那么树的高度为0）

答案：

func height<T>(of node: BinaryNode<T>?) -> Int {
    guard let tree = node else {
        return -1
    }
    return 1 + max(height(of: tree.leftChild), height(of: tree.rightChild))
}

遍历左右节点的高度，这是一个时间复杂度和空间复杂度都是 O(n) 操作。

二叉树的序列化和还原

比如下图：

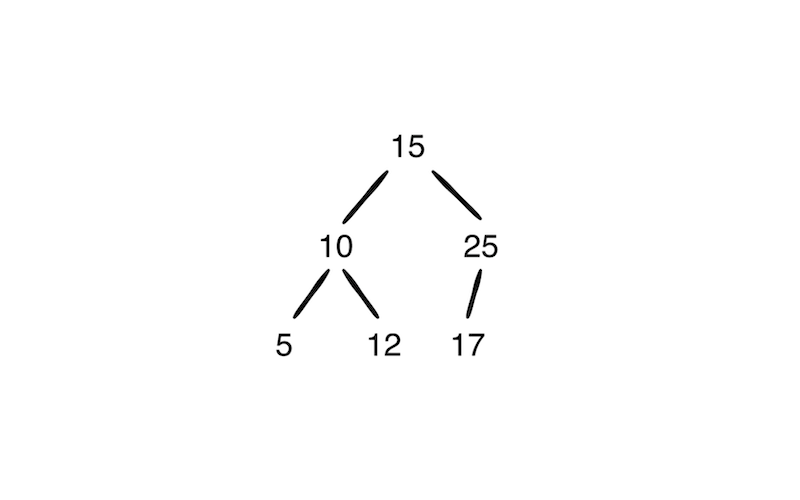
序列化输出：[15, 10, 5, nil, nil, 12, nil, nil, 25, 17, nil, nil, nil]。

答案：

由输出信息可以看出这是一个和上面类似的 Pre-orde 遍历输出类型。

添加一个辅助方法：

// 辅助输出
extension BinaryNode {
    func traverseInPreOrder(visit: (Element?) -> Void) {
        visit(value)
        if let leftChild = leftChild {
            leftChild.traverseInPreOrder(visit: visit)
        } else {
            visit(nil)
        }
        if let rightChild = rightChild {
            rightChild.traverseInPreOrder(visit: visit)
        } else {
            visit(nil)
        }
    }
}

序列化

// Time and Space O(n)
func serialize<T>(_ node: BinaryNode<T>) -> [T?] {
    var array: [T?] = []
    node.traverseInPreOrder {  array.append($0) }
    return array
}

时间复杂度 O(n)

反序列化（还原）

// Time O(n*n)
func deserialize<T>(_ array: inout [T?]) -> BinaryNode<T>? {

   // removeFirst O(n)
   guard let value = array.removeFirst() else {
       return nil
   }
   let node = BinaryNode(value: value)
   node.leftChild = deserialize(&array)
   node.rightChild = deserialize(&array)

   return node
}

测试：

print(tree)
var array = serialize(tree)
print(array)
let node = deserialize(&array)
print(node!)

输出：

 ┌──nil
┌──9
│ └──8
7
│ ┌──5
└──1
 └──0

[Optional(7), Optional(1), Optional(0), nil, nil, Optional(5), nil, nil, Optional(9), Optional(8), nil, nil, nil]
 ┌──nil
┌──9
│ └──8
7
│ ┌──5
└──1
 └──0

由于上面的代码,数组每次 removeFirst 都会导致数组里面的所有元素前向移动一位，导致反序列化的时间复杂度会是 O(n*n)

下面是反序列化的优化：

private func realDeserialize<T>(_ array: inout [T?]) -> BinaryNode<T>? {

    // removeLast O(1)
    guard let value = array.removeLast() else {
        return nil
    }
    let node = BinaryNode(value: value)
    node.leftChild = realDeserialize(&array)
    node.rightChild = realDeserialize(&array)

    return node
}

// Time and Space O(n)
func deserialize<T>(_ array: [T?]) -> BinaryNode<T>? {
    var reversed = Array(array.reversed())
    return realDeserialize(&reversed)
}

优化后的时间复杂度 O(n)。

树型数据结构 - 二叉树

实现

图像化输出

遍历算法

中序遍历

前序遍历

后序遍历

要点

试题