线性回归（目标函数的推导）经过前面多篇文章的介绍，我们知道了什么是线性回归、怎么转换求解问题、如何通过sklearn进行

跟我一起机器学习系列文章将首发于公众号：月来客栈，欢迎文末扫码关注！

1 线性回归

1.1 目标函数

经过前面多篇文章的介绍，我们知道了什么是线性回归、怎么转换求解问题、如何通过sklearn进行建模并求解以及梯度下降法的原理与推导。同时，在上一篇文章中我们还通过一个故事来交代了最小二乘法的来历，以及误差服从高斯分布的事实。下面这篇文章就来完成两个任务：线性回归的推导以及Python代码的实现

根据前面的介绍，现在我们对线性回归的目标函数做如下定义：设样本为 $(x^{(i)},y^{(i)})$ ，对样本的观测（预测）值记为 $\hat{y}^{(i)}=W^Tx^{(i)}+e^{(i)}$ ，则有：

其中 $e^{(i)}$ 表示第 $i$ 个样本预测值与真实值之间的误差， $W$ 和 $x^{(i)}$ 均为一个列向量；同时由于误差 $e^{(i)}$ 服从均值为 $0$ 的高斯分布，于是有：

f(e^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}\exp{\left(-\frac{(e^{(i)}-0)^2}{2\sigma^2}\right)}\tag{2}

于是将 $(1)$ 带入 $(2)$ 有：

f(e^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}\exp{\left(-\frac{[y^{(i)}-(W^Tx^{(i)}+b)]^2}{2\sigma^2}\right)}\tag{3}

此时请注意看等式 $(3)$ 的右边部分（从右往左看），站在 $y^{(i)}$ 的角度看，显然是随机变量 $y^{(i)}$ 是服从以 $(W^Tx^{(i)}+b)$ 为均值的正态分布（想想正态分布的表达式）。又由于此时的密度函数与参数 $\theta,x$ 有关（即随机变量 $(y^{i})$ 是 $x^{(i)},W,b$ 下的条件分布），于是有：

p(y^{(i)}|x^{(i)};W,b)=\frac{1}{\sqrt{2\pi}\sigma}\exp{\left(-\frac{[y^{(i)}-(W^Tx^{(i)}+b)]^2}{2\sigma^2}\right)}\tag{4}

到目前为止，也就是说此时真实值 $y^{(i)}$ 服从均值为 $(W^Tx^{(i)}+b)$ ，方差为 $\sigma^2$ 的正态分布。同时，由于 $(W^Tx^{(i)}+b)$ 是依赖于参数 $W,b$ 的变量，那么什么样的一组参数 $W,b$ 能够使得已知的观测值最容易发生呢？此时就要用到极大似然估计来进行参数估计：

L(\theta)=\prod_{i=1}^m p(y^{(i)}|x^{(i)};W,b)=\prod_{i=1}^m\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{[y^{(i)}-(W^Tx^{(i)}+b)]^2}{2\sigma^2}\right)\tag{5}

为了便于求解，在等式 $(5)$ 的两边同时取自然对数：

\begin{aligned}
\log L(W,b)&=\log\left\{ \prod_{i=1}^m\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{[y^{(i)}-(W^Tx^{(i)}+b)]^2}{2\sigma^2}\right)\right\}\\[3ex]
&=\sum_{i=1}^m\log\left\{\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{[y^{(i)}-(W^Tx^{(i)}+b)]^2}{2\sigma^2}\right)\right\}\\[3ex]
&=\sum_{i=1}^m\left\{\log\frac{1}{\sqrt{2\pi}\sigma}-\frac{[y^{(i)}-(W^Tx^{(i)}+b)]^2}{2\sigma^2}\right\}\\[3ex]
&=m\cdot\log\frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{\sigma^2}\frac{1}{2}\sum_{i=1}^m\left(y^{(i)}-(W^Tx^{(i)}+b)\right)^2
\end{aligned}\tag{6}

由于 $\max L(W,b)\iff\max\log L(W,b)$ ，所以：

\begin{aligned}
\max\log L(W,b)&\iff\min \frac{1}{\sigma^2}\frac{1}{2}\sum_{i=1}^m\left(y^{(i)}-(W^Tx^{(i)}+b)\right)^2\\[2ex]
&\iff\min\frac{1}{2}\sum_{i=1}^m\left(y^{(i)}-(W^Tx^{(i)}+b)\right)^2
\end{aligned}\tag{7}

于是得目标函数：

\begin{aligned}
J(W,b)&=\frac{1}{2m}\sum_{i=1}^m\left(y^{(i)}-(W^Tx^{(i)}+b)\right)^2\\[3ex]
&=\frac{1}{2m}\sum_{i=1}^m\left(y^{(i)}-\hat{y}^{(i)}\right)^2
\end{aligned}\tag{8}

1.2 求解梯度

符号说明： $y^{(i)}$ 表示第 $i$ 个样本的真实值； $\hat{y}^{(i)}$ 表示第 $i$ 个样本的预测值； $W$ 表示权重（列）向量， $W_j$ 表示其中一个分量； $X$ 表示数据集，形状为 $m\times n$ ， $m$ 为样本个数， $n$ 为特征维度； $x^{(i)}$ 为一个（列）向量，表示第 $i$ 个样本， $x^{(i)}_j$ 为第 $j$ 维特征

\begin{aligned}
J(W,b)&=\frac{1}{2m}\sum_{i=1}^m\left(y^{(i)}-\hat{y}^{(i)}\right)^2=\frac{1}{2m}\sum_{i=1}^m\left(y^{(i)}-(W^Tx^{(i)}+b)\right)^2\\[4ex]
\frac{\partial J}{\partial W_j}&=\frac{\partial }{\partial W_j}\frac{1}{2m}\sum_{i=1}^m\left(y^{(i)}-(W_1x^{(i)}_1+W_2x^{(i)}_2\cdots W_nx^{(i)}_n+b)\right)^2\\[3ex]
&=\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}-(W_1x^{(i)}_1+W_2x^{(i)}_2\cdots W_nx^{(i)}_n+b)\right)\cdot(-x_j^{(i)})\\[3ex]
&=\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}-(W^Tx^{(i)}+b)\right)\cdot(-x_j^{(i)})\\[4ex]
\frac{\partial J}{\partial b}&=\frac{\partial }{\partial b}\frac{1}{2m}\sum_{i=1}^m\left(y^{(i)}-(W^Tx^{(i)}+b)\right)^2\\[3ex]
&=-\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}-(W^Tx^{(i)}+b)\right)\\[3ex]
\end{aligned}\tag{9}

此时我们便得到了目标函数，梯度的计算公式：

\begin{aligned}
J(W,b)&=\frac{1}{2m}\sum_{i=1}^m\left(y^{(i)}-(W^Tx^{(i)}+b)\right)^2\\[3ex]

\frac{\partial J}{\partial W_j}&=\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}-(W^Tx^{(i)}+b)\right)\cdot(-x_j^{(i)})\\[4ex]
\frac{\partial J}{\partial b}&=-\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}-(W^Tx^{(i)}+b)\right)\\[3ex]
\end{aligned}\tag{10}

1.3 矢量化计算公式

为了在编程时高效的计算，我们需要对公式(10)进行矢量化：

\begin{aligned}
\hat{y}&=np.matmul(X, W) + b\\[1ex]
J(W,b) &= 0.5 * (1 / m) * np.sum((y - \hat{y}) ** 2)\\[1ex]
\frac{\partial J}{\partial W}&=-\frac{1}{m} np.dot(X.T,(y-\hat{y}))\\[1ex]
\frac{\partial J}{\partial b}&=-\frac{1}{m} np.sum(y-\hat{y})\\
\end{aligned}

这里有一个小技巧值得分享，当我们在矢量化公式的时，如果不知道到底哪个变量该放在或者要不要转置，那么就带上变量的维度一起来算。例如从公式(10)中可以看出 $W_j$ 的梯度计算公式大致长成那样，所有矢量化后的结果也差不多是那个形式，同时 $W$ 的形状是 $[n\times 1]$ ，真实值减去预测值后的形状为 $[m\times 1]$ ，因此在和 $X$ 计算后为了得 $W$ 的形状，那么只能是一个 $[n\times m]$ 的矩阵乘以 $[m\times 1]$ 的矩阵才可能的那样的结果。故，就应该把 $X.T$ 放在前面。

2 手动实现

以波士顿房价预测模型为例进行求解，由于篇幅有限只列出关键部分，完整代码见[1]。

def prediction(X, W, bias):#预测
    return np.matmul(X, W) + bias  # [m,n] @ [n,1] = [m,1]

def cost_function(X, y, W, bias):# 代价函数
    m, n = X.shape
    y_hat = prediction(X, W, bias)
    return 0.5 * (1 / m) * np.sum((y - y_hat) ** 2)

在写代码的时候可以在后边备注上维度，这样不容易出错，debug也容易。

def gradient_descent(X, y, W, bias, alpha):
    m, n = X.shape
    y_hat = prediction(X, W, bias)
    grad_w = -(1 / m) * np.matmul(X.T, (y - y_hat))  
    # [n,m] @ [m,1] = [n,1]
    grad_b = -(1 / m) * np.sum(y - y_hat)  # 求解梯度
    W = W - alpha * grad_w  # 梯度下降
    bias = bias - alpha * grad_b
    return W, bias

可以看到，对于梯度的求解就是上面公式(10)矢量化后的样子，然后运用梯度下降。

def train(X, y, ite=200):
    m, n = X.shape  # 506,13
    W = np.random.randn(n, 1)
    b = 0.1
    alpha = 0.2
    costs = []
    for i in range(ite):
        J = cost_function(X, y, W, b)
        costs.append(J)
        W, b = gradient_descent(X, y, W, b, alpha)
    y_pre = prediction(X, W, b)
    print("MSE: ", MSE(y, y_pre))
    return costs

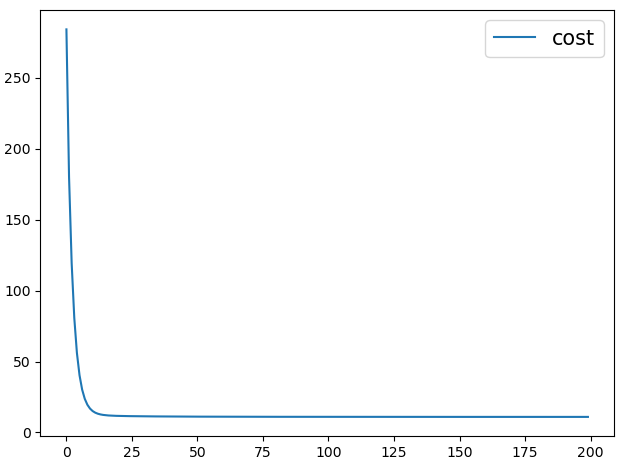
开始训练，迭代次数（也就是往谷底跳的次数）默认为200，然后返回历史损失值。

if __name__ == '__main__':
    x, y = load_data()
    train_by_sklearn(x, y)
    costs = train(x, y)
    plt.plot(range(len(costs)), costs, label='cost')
    plt.legend(fontsize=15)
    plt.tight_layout()  # 调整子图间距
    plt.show()
#输出结果：
MSE:  21.894831181729206
MSE:  21.901070160392404

从下图也可以看出，大约在25次迭代后目标函数就基本开始收敛了。

3 总结

通过本篇文章的介绍，对于线性回归的主要内容也算到此结束了，对于其它细枝末节的地方（例如学习率的选择、特征标准化等），在后续模型改善部分再介绍。

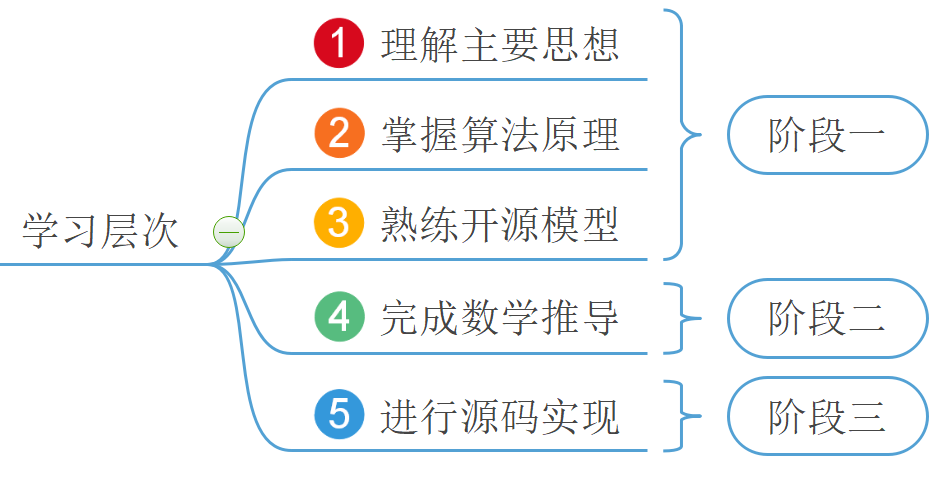
总结一下，如上图所示笔者首先通过三篇文章介绍了线性回归模型第一阶段的主要内容，通过这三片文章你可以大致知道拿到一个问题如何通过开源的sklearn库进行线性回归建模。虽然阶段一的内容并没有从数学的角度来完成对于线性回归的论证，但是其包含了学习一个算法并快速入门的路线。然后笔者接着通过两篇半文章介绍了梯度下降算法的介绍、误差的正太分布特性和目标函数的推导，完成了线性回归第二阶段的学习。这个阶段一般都是算法从数学层面上的理论依据，尤其是统计机器学习更是依赖于这个过程，但是这部分通常来说都有一定的难度。例如在接受SVM的时候，笔者可能就只会介绍到阶段一了。最后，笔者通过本篇内容的后半部分完成了线性回归模型源码的实现，当然这也是建立在第二阶段的基础上。本次内容就到此结束，感谢阅读！

若有任何疑问，请发邮件至moon-hotel@hotmail.com并附上文章链接，青山不改，绿水长流，月来客栈见！

引用

[1] 示例代码及练习： github.com/moon-hotel/…