前言

本篇文章将会介绍最后一个数据结构，它也是很简单的，并且在生活中的应用也是很广泛的，下面就让我们去详细的了解它

基本概念

图结构和树结构是很类似的，也是由节点和边组成的，树结构可以说是图结构的特例。图在生活中的应用是非常多的，比如地铁线路、互联网线路、我们前端最熟悉的Web结构、还有我们前面讲过的区块链技术。

还是看图容易理解哈，那么继续来了解它的基本术语吧

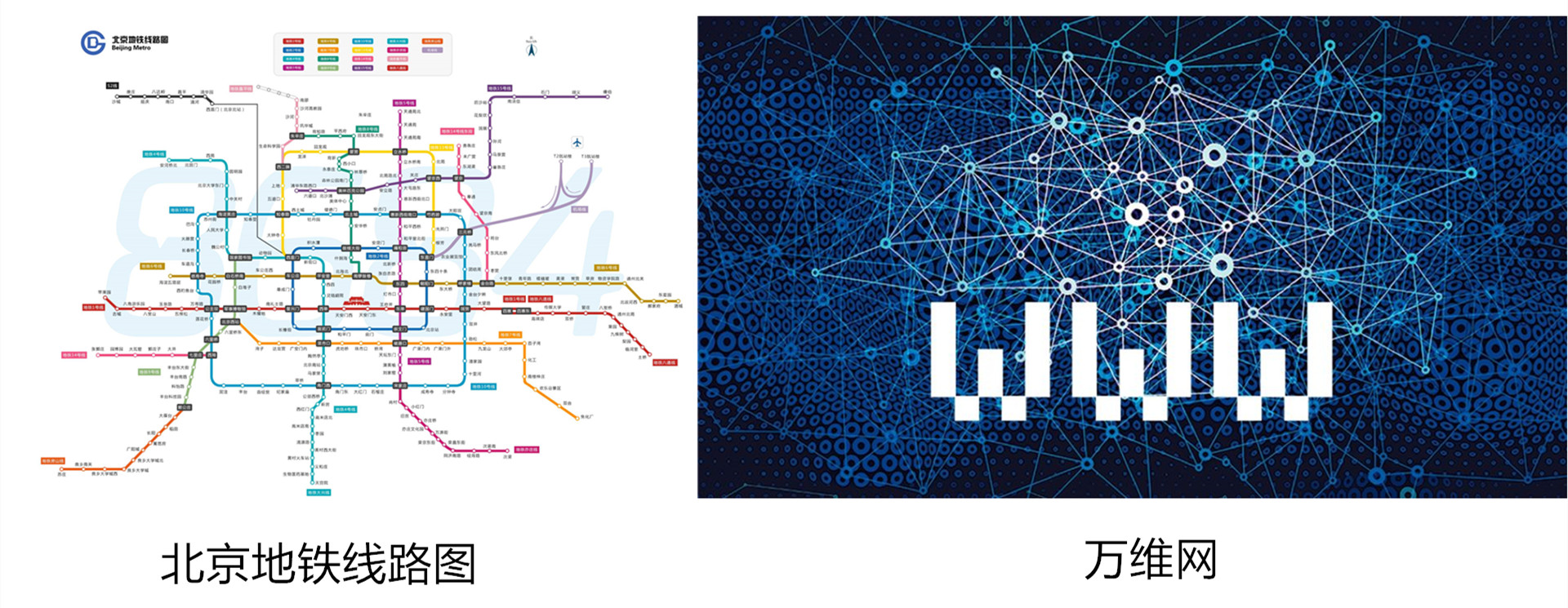
• 顶点（Vertex）——也称作节点（Node），是图的基本组成部分。
• 边（Edge）——也成为弧（Arc），连接两个顶点，可以是有向（也就是有箭头）或者无向（也就是无箭头）的，有向边组成的图称作有向图，无向边组成的图称为无向图。
• 权重（Weight）——从一个顶点到另一个顶点的“代价”，就是给边附上值，来代表不同边的“重要性”
• 路径（Path）——从一个顶点沿边到另一个顶点的序列，无权路径的长度为边的数量，有权路径的长度为所有边权重的和
• 圈（Cycle）——首位节点相同的路径
• 有向无圈图（directed acyclic graph即DAG）——有向图中不存在任何圈 这些术语都明白之后我们就来用JavaScript简单的实现一下图结构

//实现顶点类
class Vertex {
    constructor(key) {
        this.key = key
        //存储邻顶点 和它们之间的权重
        this.connectedTo = {}
    }
    addNeighbor(nbr, weight = 0) {
        //设置权重
        this.connectedTo[nbr.key] = weight
    }
    getConnection() {
        //获取与它连接的顶点
        return Object.keys(this.connectedTo)
    }
    getKey() {
        return this.key
    }
    getWeight(nbr) {
        return this.connectedTo[nbr.key]
    }
}
class Vertex {
    constructor(key) {
        this.key = key
        //存储邻顶点 和它们之间的权重
        this.connectedTo = {}
    }
    addNeighbor(nbr, weight = 0) {
        //设置权重
        this.connectedTo[nbr.key] = weight
    }
    getConnection() {
        //获取与它连接的顶点
        return Object.keys(this.connectedTo)
    }
    getKey() {
        return this.key
    }
    getWeight(nbr) {
        return this.connectedTo[nbr.key]
    }
}
class Graph {
    constructor(isDirected = false) {
        //是否为有向图
        this.isDirected = isDirected;
        this.vertList = {}
    }
    addVertex(key) {
        this.vertList[key] = new Vertex(key)
    }
    getVertex(key) {
        if (key in this.vertList) {
            return this.vertList[key]
        } else {
            return null
        }
    }
    addEdge(f, t, cost) {
        if (!this.vertList.hasOwnProperty(f)) {
            this.addVertex(f)
        }
        if (!this.vertList.hasOwnProperty(t)) {
            this.addVertex(t)
        }
        this.vertList[f].addNeighbor(this.vertList[t], cost)
        //如果为无向图则在另一个顶点也存入它的顶点
        if (!this.isDirected) {
            this.vertList[t].addNeighbor(this.vertList[f], cost)
        }
    }
    getVertices() {
        return this.vertList
    }
}

这里还实现了一个定点类，用来存储与它相连的顶点。代码比较简单，因为只是一个图的简单实现，可以自己敲一敲，很好理解。

广度优先遍历

广度优先遍历（Breadth First Search），也就是我们常说的BFS。顾名思义就是遍历的时候以广度为主，只要还有和此顶点直接相连的顶点，那么就先遍历那个顶点，直到这些顶点都遍历完，再把“目光”移到下一个顶点。还是很好理解的，那么我们就用JavaScript代码来实现一下吧，我们实现它需要为顶点类添加

• 距离distance——从起始顶点到当前顶点的路径长度
• 前驱顶点predecessor——可以反向追溯到起点
• 颜色color——表示顶点状态，未发现（白色）、已发现（灰色）、完成探索（黑色）

还需要前面实现过的队列来决定下一个要探索的顶点。

class BFSVertex extends Vertex {
    constructor(key) {
        super(key)
        this.distance = Number.MAX_SAFE_INTEGER
        this.predecessor = null
        this.color = 'white'
    }
    setDistance(num) {
        this.distance = num
    }
    setPred(pred) {
        this.predecessor = pred
    }
    setColor(color) {
        this.color = color
    }
    getColor() {
        return this.color
    }
    getDistance() {
        return this.distance
    }
    getPred() {
        return this.predecessor
    }
}
function bfs(graph, start) {
    //设置起始顶点距离为0
    start.setDistance(0)
    let vertQueue = new Queue()
    //将起始顶点入队
    vertQueue.enqueue(start)
    //队列不为空就一直循环取顶点
    while (vertQueue.size() > 0) {
        let currentVert = vertQueue.dequeue()
        //遍历与当前顶点相连的顶点
        const vertexs = graph.getVertices()
        for (let nbr of currentVert.getConnection()) {
            //如果未访问过
            if (vertexs[nbr].getColor() === 'white') {
                //设置为已访问
                vertexs[nbr].setColor('grey')
                //设置前驱顶点
                vertexs[nbr].setPred(currentVert)
                //距离加1
                vertexs[nbr].setDistance(currentVert.getDistance() + 1)
                //入队
                vertQueue.enqueue(vertexs[nbr])
            }
        }
        //设置已探索完成
        currentVert.setColor('black')
    }
}

注释写的比较详细，自己根据思路实现一下，比较简单。

深度优先遍历

深度优先遍历是和广度优先遍历相对应的，它是先把和顶点连着的一个顶点探索到尽头，然后再去探索另一个与它直接相连的顶点，也是很好理解哈，那我们直接看代码吧。

class DFSVertex extends BFSVertex {
    constructor(key) {
        super(key)
        this.discover = 0
        this.finish = 0
    }
    setDiscover(num) {
        this.discover = num
    }
    getDiscover() {
        return this.discover
    }
    setFinish(num) {
        this.finish = num
    }
    getFinish() {
        return this.finish
    }
}
class DFSGraph extends Graph {
    constructor(key) {
        super(key)
        this.time = 0
    }
}
function dfs(graph) {
    //全部置为未访问
    let vertexs = graph.getVertices()
    for (let vertex in vertexs) {
        vertexs[vertex].setColor('white')
    }
    //再遍历一遍，如果有为访问状态则调用访问方法
    for (let vertex in vertexs) {
        if (vertexs[vertex].getColor() === 'white') {
            dfsVisit(graph, vertexs[vertex])
        }
    }
}

function dfsVisit(graph, start) {
    //设置成已访问
    start.setColor('grey')
    graph.time += 1
    //记录开始探索时间
    start.setDiscover(graph.time)
    const vertexs = graph.getVertices()
    //遍历它的邻节点，如果有未访问则递归调用访问方法
    for (let nextVert of start.getConnection()) {
        if (vertexs[nextVert].getColor() === 'white') {
            vertexs[nextVert].setPred(start)
            dfsVisit(graph, vertexs[nextVert])
        }
    }
    //设置成已探索
    start.setColor('black')
    graph.time += 1
    //记录结束探索时间
    start.setFinish(graph.time)
}

我们需要在Graphs类中加入time属性，来记录帮助记录每个顶点的开始探索时间和结束探索时间，这个的作用在下面的拓扑排序中会非常明显。代码里的注释也是很详细的，还是要自己实现一下。

拓扑排序

我们每天都要做很多工作，有些工作相互之间是有依赖关系的，那我们应该以什么样的顺序来做完这些事效率才会最高呢？拓扑排序就是来解决这类问题的，即从工作流程图得到工作次序排列的算法。拓扑排序处理的必须是一个DAG，我们在前面提到过，也就是不存在任何圈的有向图，最后会输出一个顶点的线性序列。拓扑排序可以利用DFS很好的来实现。根据记录的完成探索时间，从大到小排序即可。放一个图来理解一下

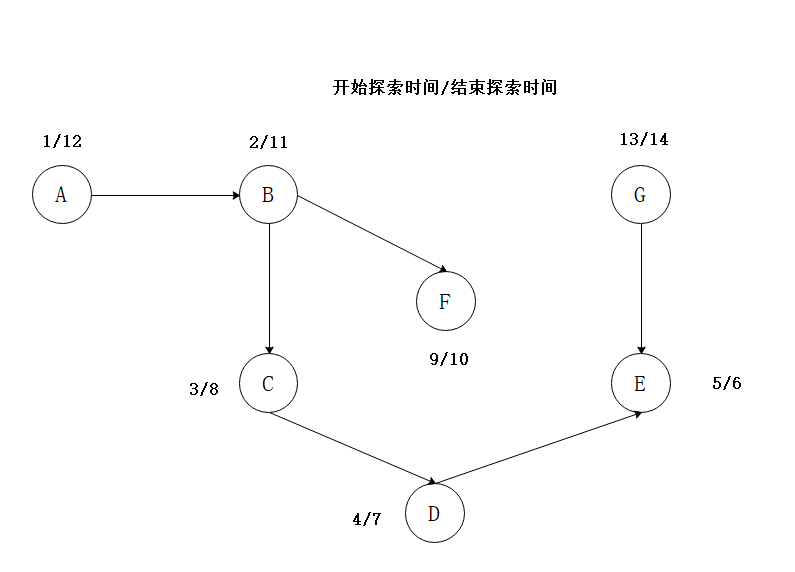
最短路径

最短路径问题在我们的生活中是非常常见的，尤其是我们这个行业，更应该是非常熟悉。就是在路由器寻址的时候，路由器选择传播速度最快的路径，就像选择带权图权重最小的（最短）路径一样。这个方法和BFS很相似。我们介绍一个解决带权最短路径问题的经典算法——Dijkstra算法。思路和BFS的差不多，就是多了一个变量来存储当前顶点和相邻顶点的权重值，并通过重排优先队列进行排序。具体代码如下

function dijkstra(graph, start) {
    //创建优先队列
    let preQueue = new PriorityQueue()
    //起始顶点置为0
    start.setDistance(0)
    const vertexs = graph.getVertices()
    //循环入队
    for (let vert in vertexs) {
        preQueue.enqueue(vertexs[vert])
    }
    while (!preQueue.isEmpty()) {
        //出队
        let currentVert = preQueue.dequeue()
        //循环它的相邻顶点
        for (let nextVert of currentVert.getConnection()) {
            //计算新的距离
            let newDist = currentVert.getDistance() + currentVert.getWeight(vertexs[nextVert])
            //比现有距离小就更新
            if (newDist < vertexs[nextVert].getDistance()) {
                vertexs[nextVert].setDistance(newDist)
                vertexs[nextVert].setPred(currentVert)
            }
        }
    }
}

这里使用了优先队列，我们在上一篇已经讲过了优先队列，在出队的时候会根据顺序出队，我们只需要把其中用来排序的code改为我们的distance就行了

最小生成树

有些人爱玩网络游戏，而有些人爱听网络广播。这些都需要服务器去以广播的方式把消息发送给所有的用户，比如打游戏时一个人的位置，需要发给所有跟他一起玩的用户。那么怎么发送呢，可以用单播，即给每个用户传输一个，这样的话中途的路由器可能会处理多次重复的消息，产生许多额外流量。又有人提出了洪水解法，即给每一个路由器都发送一个，这样会造成很多路由器不断受到相同的消息，永不停止，后来又加了TTL加以限制，但是还是产生非常大的流量。那有没有更优的解法呢？那就是我们要说的最小生成树的解法。

最小生成树就是权重最小而且拥有图中所有顶点和最少数量的边以保持连通的子图。这里我们介绍一种解决最小生成树的算法——Prim算法，它是贪心算法的一种，即每一步都先搜索权重最小的边。思路也很简单，只要顶点还没有全，就找一个权重最小的、一端连接树中顶点、一端连接不在树中的顶点的边将其添加到树中。具体代码如下

function prim(graph, start) {
    let preQueue = new PriorityQueue()
    start.setDistance(0)
    const vertexs = graph.getVertices()
    for (let vert in vertexs) {
        preQueue.enqueue(vertexs[vert])
    }
    while (!preQueue.isEmpty()) {
        let currentVert = preQueue.dequeue()
        for (let nextVert of currentVert.getConnection()) {
            let newDist = currentVert.getWeight(vertexs[nextVert])
            if (preQueue.isInclude(vertexs[nextVert]) && newDist < vertexs[nextVert].getDistance()) {
                vertexs[nextVert].setDistance(newDist)
                vertexs[nextVert].setPred(currentVert)
            }
        }
    }
}

代码思路和最小路径差不多，只不过这里只是根据权值来向树中添加点，没有进行距离的计算。

小结

图是一个比较简单的数据结构，学起来也比较容易。虽然简单我们也要掌握它，只有掌握它才能在以后有可能用到的时候发挥它的作用。本篇是《快速入门数据结构与算法》系列的最后一篇，这是我第一次写文章，想着也是给自己做做笔记，加深印象，如果可能的话能帮到一些人那肯定是更好的。强迫自己输出文章是非常有益的，有些东西当你学过之后也许自认为记住了、会了，但是让你给别人讲不一定能讲的清楚、讲的明白。只有能给别人讲明白，自己才是真的明白了。在写文章的时候能够找到很多缺漏，能够真正的去理解，给自己吸收的知识做一个输出对自己的提高很大。一个月写下来虽然阅读量很少，点赞也很少，但是写完之后自己的这些知识的牢固性让自己感到安心，感到自己真正学到知识了，时间没有白费，就很开心了。这也是能够支撑着我，让我坚持写下去的动力。这各系列只是一个开始，以后会更加努力的去学习，汲取知识再输出，更加频繁的去写文章。某大佬说过“如果每天写一篇文章，写个一百篇也能成为大佬”，像我这种小白一天一篇估计够呛，消化的有点慢，但是我一定尽力，向大佬进发，我是要成为大佬的男人！加油！！！