浅谈javascript动态规划DP算法

一、入门案例

首先，我们来看一个典型的例子，通过这个例子来了解什么是动态规划。

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

这个题目，在部分面试中，出现的频率也不低，就是考察动态规划算法的DP。 那我们应该怎么实现？

1、设定一个数组，存放到达第n层的跳法

假设这么一个数组 arr，arr[n] 表示到n层的跳法，arr[n-1] 表示到n-1层的跳法。 具体arr[n]的值等于多少，我们先暂时不用操心。

2、倒着分析，找关系

正常情况，假如从第1层往上爬，可以爬2层，也可以爬3层。我们这么按照正方向去枚举，找规律也太难了。所以，我们要倒着来分析。

假如青蛙爬上来了，无非是从n-1(倒数第1层)爬上来的，或者是n-2(倒数第2层)爬上来的。 假如青蛙到达了第n-1层了，此时累计的跳法就是 arr[n-1]; 假如青蛙到达了第n-2层了，此时累计的跳法就是 arr[n-2];

那么，到达第n层的总跳法，就是：

arr[n] = arr[n-1] + arr[n-2]

现在来看，是不是有点想之前解数学题的 归纳法？

3、处理极值

很明显，楼梯只能是正数。 arr[n] = arr[n-1] + arr[n-2]，这里的n，假如为为1的时候，需要特殊处理。

arr[1]很明显是等于1的，因为到达第1层，只有1种跳法。 arr[2]很明显是等于2的，因为达到第2层，有2种跳法。

所以

arr[1] = 1;
arr[2] = 2;
arr[0] = 0;

所以最终实现方法如下：

function dpClimb(n){
    if(n<=2){
        return n;// n = 0,1,2时，对应的跳法也是0，1，2
    }
    return dpClimb(n-1) + dpClimb(n-2)
}

刚才不是说存放到一个数组里面去了吗？ 怎么变成了 dpClimb(n) 和dpClimb(n-1)了？ 其实这里，dpClimb(n) 就是返回一个值，这个值表示到达第n层的跳法，(你可以理解为一个隐形的数组)。用到了递归。同时，我们用到了一些缓存。把前两层的跳法缓存起来，我们就知道第3层的跳法了。

测试一下爬20层楼梯，有多少种爬法：

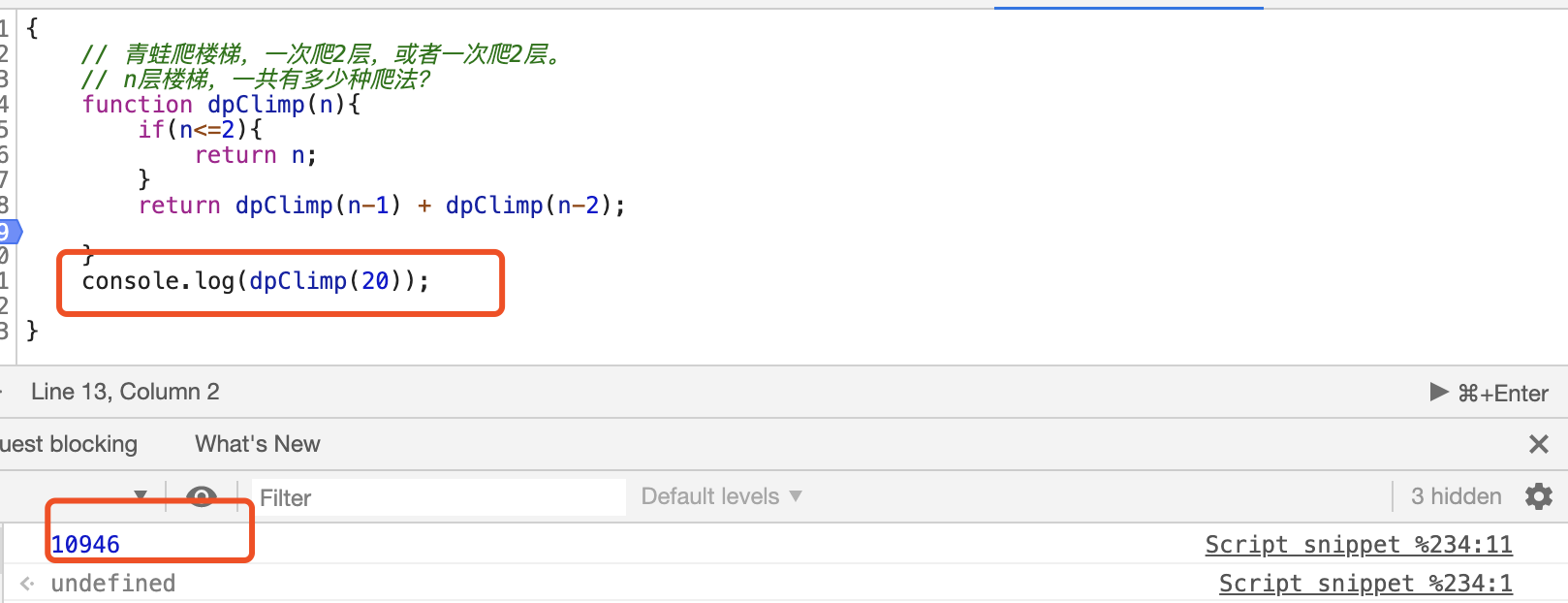
二、案例深入

上一个可以理解为一维数组，这次我们来一个二维数组看看。

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。问总共有多少条不同的路径？

按照上一步的做法，我们一步一步的实现这个。

1、设定一个数组，存放到达第n层的跳法。

现在是二维数组了，我们用arr[m - 1][n -1]表示到达第[m,n]格子的路径总和。。 为什么是 arr[m - 1][n -1]呢？因为而且每次只能移动一个格子，且数组坐标是[0,0]开始的。

2、倒着分析，找关系

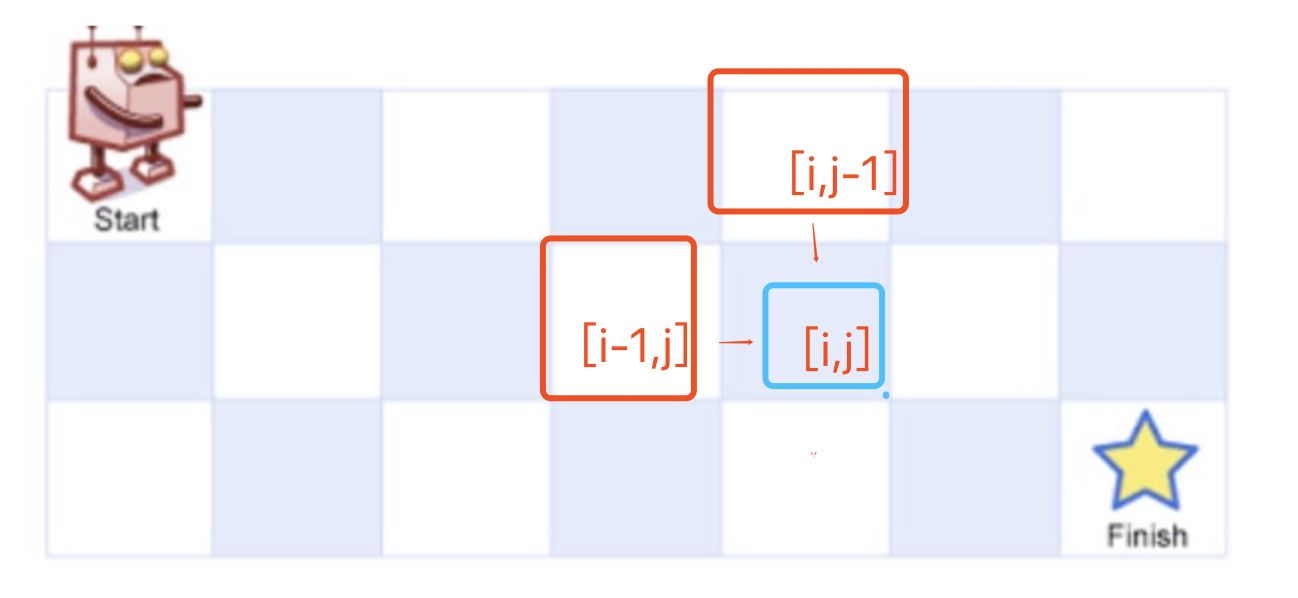
假定，机器人在途中的[i，j]这个地方，那么它的上一步的走法，只可能是从 [i,j-1]，或者[i-1,j]这个地方走过来。 所以，到达[i,j]这个地方的路径总和为：

arr[i][j] = arr[i-1][j] + arr[i][j-1]

3、处理极值(初始值)

这里，我们只能从坐标[0,0]开始，因此i，j都是大于等于0的。 同时，当机器人沿着格子边缘一直横着走或者竖着走的时候，同时，题目要求机器人只能往下，或者往右走（不能往左，往上走）。所以，让机器人处于格子边缘时，不管在哪个格子，到达这个格子的路径总和只能是1。

所以，我们得出极值为：

arr[i][0] = 1;
arr[0][j] = 1;

代码实现

// 首先定义一个空的JavaScript二维数组
function Array2(m,n){
    let _array2 = new Array(m);
    for(let i=0;i<m;i++){
        let emptyArr = new Array(n);
        for(let j=0;j<n;j++){
            emptyArr[j] = 0;// 每一项初始值为0，防止后面做加减运算出现NaN的情况
        }
        _array2[i] = emptyArr;
    }
    return _array2;
}
console.log(Array2(6,7));

验证一下这个二维数组方法是否是我们想要的：

得到了这个二维数组，我们就可以拿来存储arr[i][j]了。

主要代码如下:

function totalPath(m,n){
    let arr = Array2(m,n);
    // 横着一直走的极值情况
    for(let i=0;i<m;i++){
        arr[i][0] = 1;
    }
    // 竖着一会往下走的极值情况
    for(let j=0;j<n;j++){
        arr[0][j] = 1;
    }
    // 关系归纳
    for(let i=1;i<m;i++){
        for(let j = 1;j<n;j++){
            arr[i][j] = arr[i-1][j] + arr[i][j-1];
        }
    }
    return arr[m-1][n-1];
}

我们来查看结果

console.log(totalPath(7,3));

同时，我们也能就看到那个缓存的数组，存储的到达每一个格子坐标的路径总和。

总结

从第一个例子，我们用到了递归，第二个例子，我们用到了缓存。 所以DP动态规划，可以初步理解为，利用递归+缓存，来解决某类问题。 至于时间复杂度，空间复杂度，等理解透了，再来优化。