从零开始的数据结构与算法（八）：树树是一种非线性结构，数据元素之间存在着一对多的层次关系，把它叫做“树”是因为它看起来像

1 树

1.1 定义

树是一种非线性结构，数据元素之间存在着一对多的层次关系，把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

在树结构中，每个元素称为结点，每个结点有零个或多个子结点。其前驱结点称为父结点或双亲结点，其后继称为子结点。其中：

仅有一个特定的结点没有父结点，称为根结点或树根；
没有子结点的结点称为叶结点或树叶。

空集合也是树，称为空树。下图展示了单结点树和一般的树结构。

单结点树：一般树：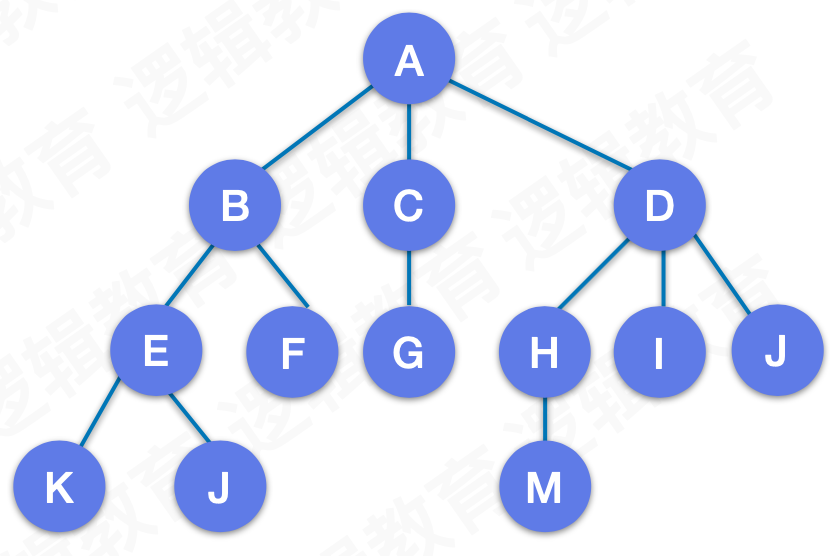

1.2 结点的度

一个结点含有的子结点的个数称为该结点的度。如上图一般树的 D 结点，它的度为 3。

1.3 结点的层次（深度）

从根开始定义起，根为第1层，根的子结点为第2层，以此类推。如上图一般树的 K 结点，它的层次（深度）为 4。

1.4 树的深度

一棵树中，最大的结点层次称为树的深度。如下图，最“深”的结点 K、J、M 的深度为 4，所以树的深度为4.

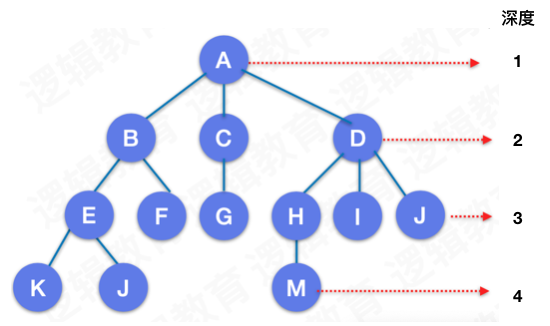
2 二叉树

2.1 定义

二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”和“右子树”。二叉树常被用于实现二叉查找树和二叉堆。

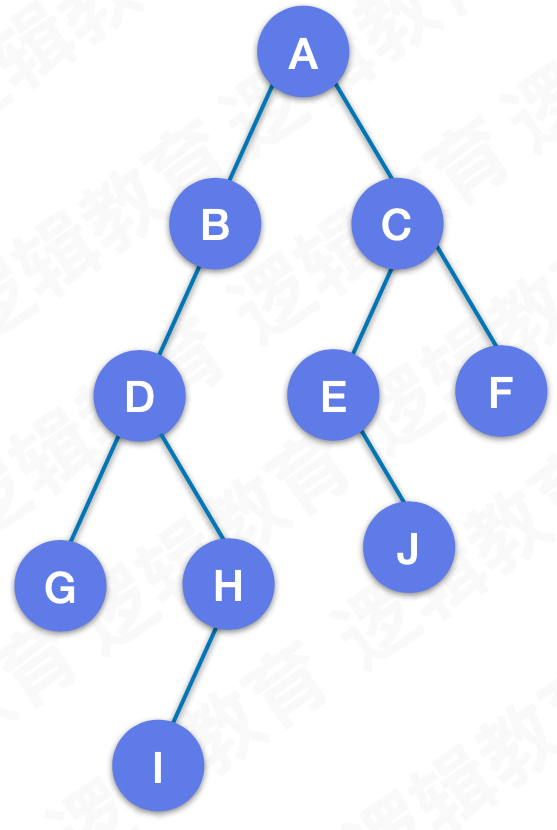
2.2 满二叉树

一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是 (2 ^ k) -1，则它就是满二叉树。

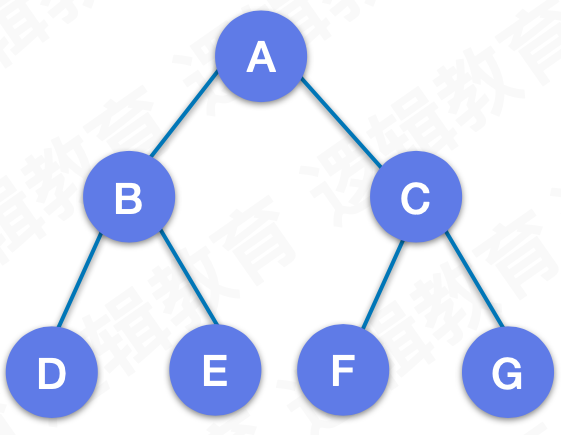
2.3 完全二叉树

对于深度为 K 的，有 n 个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从 1 至 n 的结点一一对应时称之为完全二叉树。

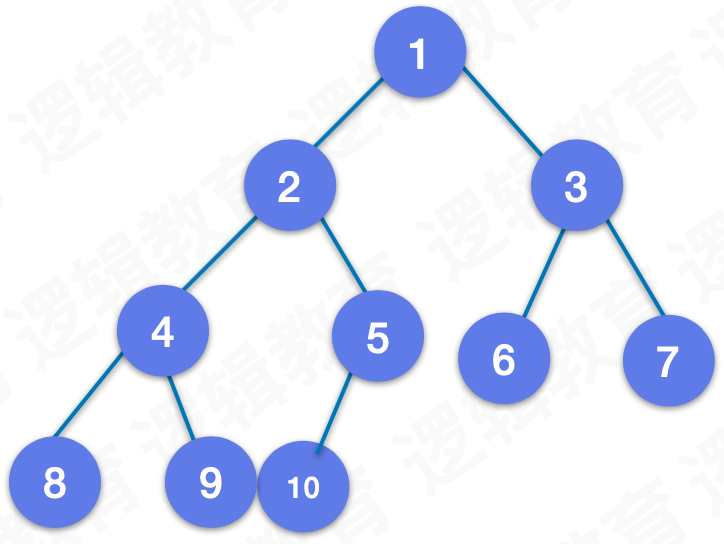
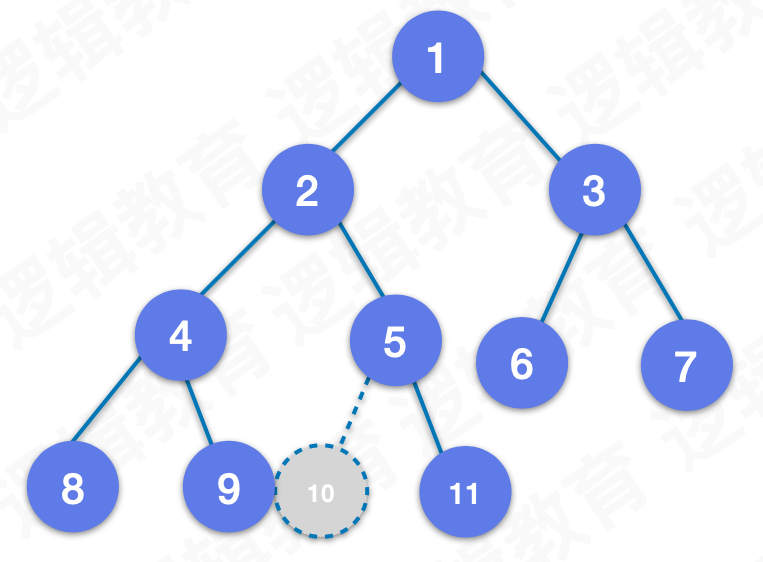
下图则不为完全二叉树：

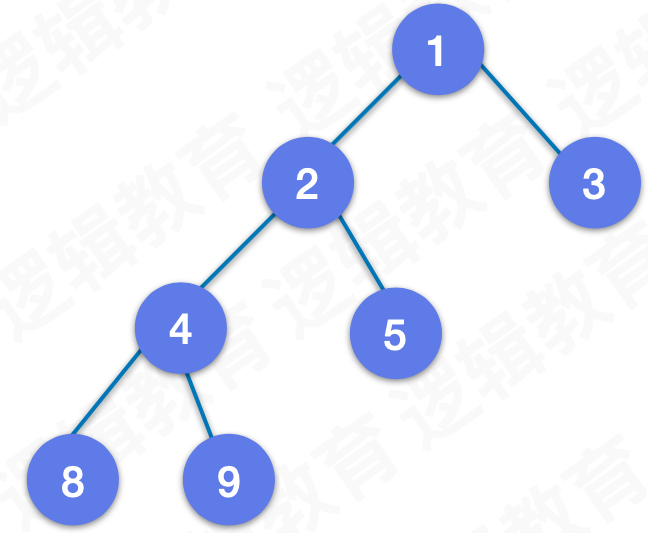
非完全二叉树非完全二叉树2

2.4 二叉树的性质

深度为 k 的二叉树，最多拥有 2 ^ k - 1 个结点。

深度为 4 的满二叉树共有 2 ^ 4 - 1 = 15 个结点。

第 k 层上最多有 2 ^ (k - 1) 个结点。

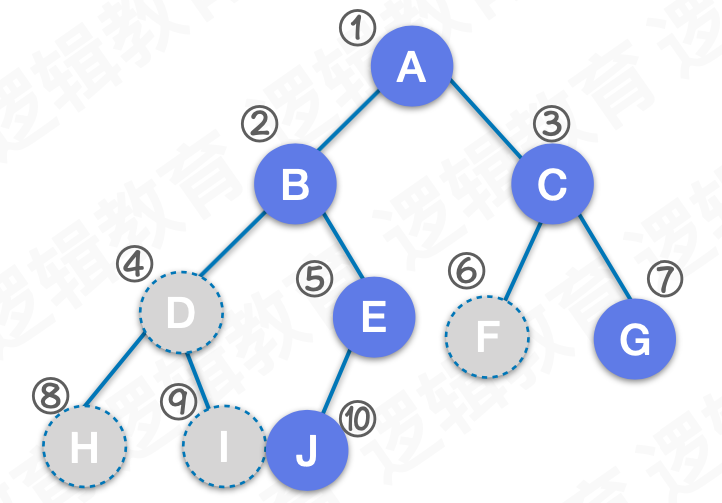
深度为 3 的结点共有 2 ^ (3 - 1) = 4 个，如上图结点 4、5、6、7。

对于任意的二叉树，终端结点数为 n0，度为 2 的结点数为 n1，则有 n0 = n1 + 1。

如上图，终端结点 8、9、10、6、7，n0 = 5，度为 2 的结点 1、2、3、4，n1 = 4。n0 = n1 + 1。

具有 n 个结点的完全二叉树，其深度为 log2(n) + 1。（同性质1）
有 n 个结点的完全二叉树，按照从上之下、从左至右的顺序从 1 开始编号，对于编号为 i 的结点则有以下性质：
1. 当 i = 1（非根结点）时，为根结点，无父结点。
2. 当 i > 1（非根结点）时，其父结点编号为 i / 2。
3. 结点 i 的左子结点编号为 2 * i，前提是 2 * i < n，否则无左子结点。
4. 结点 i 的右子结点编号为 2 * i + 1，前提是 2 * i + 1 < n，否则无右子结点。

2.5 二叉树的遍历

层序遍历：从根结点开始从上往下逐层遍历，在同一层中从左向右遍历各个结点。

前序遍历：先访问结点本身，然后前序遍历其左结点，最后前序遍历其右结点。

中序遍历：先中序遍历其左结点，然后访问结点本身，最后中序遍历其右结点。

后序遍历：先后序遍历其左结点，然后后序遍历其右结点，最后访问结点本身。

层序遍历：1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10

前序遍历：1 - 2 - 4 - 8 - 9 - 5 - 10 - 3 - 6 - 7

中序遍历：8 - 4 - 9 - 2 - 10 - 5 - 1 - 6 - 3 - 7

后序遍历：8 - 9 - 4 - 10 - 5 - 2 - 6 - 7 - 3 - 1

3 顺序存储二叉树

将二叉树按照层次遍历的顺序存储到顺序结构中，对应关系如下所示：

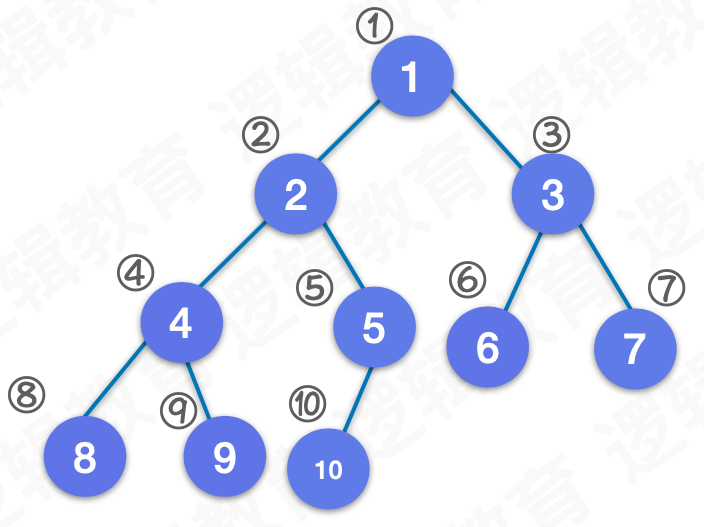
如果不是完全二叉树，则在对应完全二叉树空缺的地方置空存储。由于结点的个数随深度呈指数增长，非完全二叉树在顺序存储中会产生内存的浪费，所以一般情况下都会将数据结构转换为完全二叉树进行存储。

3.1 结构定义

/// 设置队列的长度
#define MAXSIZE 100             // 数组大小
ElementType Nil = INT32_MIN;    // 定义空值
typedef ElementType SqBiTree[MAXSIZE];    // 通过数组保存树

3.2 常用方法

/// 初始化二叉树
static Status initBinaryTree(SqBiTree t) {
    for (int i = 0; i < MAXSIZE; i++) {
        t[i] = Nil;
    }
    return SUCCESS;;
}

/// 清空二叉树
#define clearBinaryTree initBinaryTree

/// 判断为空
static int isEmptyBinaryTree(SqBiTree t) {
    if (t[0] == Nil) {
        return 1;
    }
    return 0;
}

3.3 获取深度

/// 获取二叉树的深度
static int getBinaryTreeDepth(SqBiTree t) {
    // 深度
    int depth = -1;
    // 从后遍历，寻找最后一个不为空的索引
    int i;
    for (i = MAXSIZE - 1; i >= 0; i--) {
        if (t[i] != Nil) {
            break;
        }
    }
    // 每层的最后一个元素索引为 2 ^ depth - 2，
    do {
        depth++;
    } while (powl(2, depth) - 2 < i);
    return depth;
}

3.4 取值

/// 获取目标位置上结点的值
/// @param t 根结点
/// @param level 目标结点深度
/// @param order 目标结点所在层的序号
/// @param e 返回值
static Status getValueInBinaryTree(SqBiTree t, int level, int order, ElementType *e) {
    // 1 根据深度和序号得到索引
    // order - 1 : 每层的 order 规定从 1 开始，所以减一得到偏移值
    // - 1 : 序号减一为数组坐标
    int i = (int)powl(2, level - 1) + (order - 1) - 1;
    // 2 判断位置 i 是否合法
    // 2.1 数组越界
    if (i >= MAXSIZE) {
        return ERROR;
    }
    // 3 返回值
    *e = t[i];
    return SUCCESS;
}

3.5 赋值

/// 设置目标位置上结点的值
/// @param t 根结点
/// @param level 目标结点深度
/// @param order 目标结点所在层的序号
/// @param e 修改值
static Status setValueInBinaryTree(SqBiTree t, int level, int order, ElementType e) {
    // 1 根据深度和序号得到索引
    // order - 1 : 每层的 order 规定从 1 开始，所以减一得到偏移值
    // - 1 : 序号减一为数组坐标
    int i = (int)powl(2, level - 1) + (order - 1) - 1;
    // 2 判断位置 i 是否合法
    // 2.1 数组越界
    if (i >= MAXSIZE) {
        return ERROR;
    }
    // 2.2 赋非空值，但该结点没有父结点
    if (e != Nil && t[(i + 1) / 2 - 1] == Nil) {
        return ERROR;
    }
    // 2.3 赋空值，但该结点依旧有子结点
    if (e == Nil) {
        int hasLeftchild = (i * 2 + 1) < MAXSIZE && t[i * 2 + 1] != Nil;
        int hasRightchild = (i * 2 + 1) < MAXSIZE && t[i * 2 + 1] != Nil;
        if (hasLeftchild || hasRightchild) {
            return ERROR;
        }
    }
    // 3 赋值
    t[i] = e;
    return SUCCESS;
}

3.6 遍历

/// 层序遍历
static Status levelOrderTraverse(SqBiTree t) {
    int i = 0;
    while (i < MAXSIZE) {
        if (t[i] != Nil) {
            printf("%d ", t[i]);
        }
        i++;
    }
    return SUCCESS;
}

/// 前序遍历
static Status preOrderTraverse(SqBiTree t, int i) {
    // 1 打印自身结点
    if (t[i] != Nil) {
        printf("%d ", t[i]);
    }
    // 2 递归打印左结点
    int left = 2 * i + 1;
    if (left < MAXSIZE) {
        preOrderTraverse(t, left);
    }
    // 3 递归打印右结点
    int right = 2 * i + 2;
    if (right < MAXSIZE) {
        preOrderTraverse(t, right);
    }
    return SUCCESS;
}

/// 中序遍历
static Status inOrderTraverse(SqBiTree t, int i) {
    // 1 递归打印左结点
    int left = 2 * i + 1;
    if (left < MAXSIZE) {
        inOrderTraverse(t, left);
    }
    // 2 打印自身结点
    if (t[i] != Nil) {
        printf("%d ", t[i]);
    }
    // 3 递归打印右结点
    int right = 2 * i + 2;
    if (right < MAXSIZE) {
        inOrderTraverse(t, right);
    }
    return SUCCESS;
}

/// 后序遍历
static Status postOrderTraverse(SqBiTree t, int i) {
    // 1 递归打印左结点
    int left = 2 * i + 1;
    if (left < MAXSIZE) {
        postOrderTraverse(t, left);
    }
    // 2 递归打印右结点
    int right = 2 * i + 2;
    if (right < MAXSIZE) {
        postOrderTraverse(t, right);
    }
    // 3 打印自身结点
    if (t[i] != Nil) {
        printf("%d ", t[i]);
    }
    return SUCCESS;
}

/// 简单地打印二叉树结构，仅用于测试
static Status display(SqBiTree t) {
    int maxDepth = getBinaryTreeDepth(t);
    char s[maxDepth];
    for (int depth = 0; depth < maxDepth; depth++) {
        int i;
        for (i = 0; i < ((maxDepth - depth)); i++) {
            s[i] = ' ';
        }
        s[i] = '\0';
        int count = powl(2, depth);
        for (int order = 0; order < count; order++) {
            printf("%s", s);
            int e = t[(int)powl(2, depth) + order - 1];
            if (e == Nil) {
                printf(" ");
            } else {
                printf("%d", e);
            }
        }
        printf("\n");
    }
    return SUCCESS;
}

3.7 使用

int main() {    
    // 声明二叉树
    SqBiTree t;
    printf("初始化二叉树\n");
    initBinaryTree(t);
    
    // 层序次序构建二叉树
    for (int i = 0; i < 10; i++) {
        t[i] = i + 1;
    }
    
    printf(isEmptyBinaryTree(t) ? "二叉树为空\n" : "二叉树不为空\n");
    printf("二叉树的深度为 %d\n", getBinaryTreeDepth(t));
    
    display(t);
    
    printf("层序遍历：");
    levelOrderTraverse(t);
    printf("\n");
    
    printf("前序遍历：");
    preOrderTraverse(t, 0);
    printf("\n");
    printf("中序遍历：");
    inOrderTraverse(t, 0);
    printf("\n");
    printf("后序遍历：");
    postOrderTraverse(t, 0);
    printf("\n");
    
    ElementType e;
    int level = 3;
    int order = 2;
    getValueInBinaryTree(t, level, order, &e);
    printf("第 %d 层第 %d 个结点的值为 %d\n", level, order, e);
    
    e = 777;
    setValueInBinaryTree(t, level, order, e);
    printf("修改第 %d 层第 %d 个结点的值为 %d\n", level, order, e);
    
    display(t);
    
    return 0;
}

打印结果：

初始化二叉树
二叉树不为空
二叉树的深度为 4
    1
   2   3
  4  5  6  7
 8 9 10          
层序遍历：1 2 3 4 5 6 7 8 9 10 
前序遍历：1 2 4 8 9 5 10 3 6 7 
中序遍历：8 4 9 2 10 5 1 6 3 7 
后序遍历：8 9 4 10 5 2 6 7 3 1 
第 3 层第 2 个结点的值为 5
修改第 3 层第 2 个结点的值为 777
    1
   2   3
  4  777  6  7
 8 9 10

4 链式存储二叉树

4.1 结构定义

/// 二叉树结点结构
typedef struct TreeNode {
    ElementType data;           // 数据域
    struct TreeNode *lch, *rch; // 左子树与右子树
} *TreeNodePtr;

4.2 常用方法

/// 初始化二叉树
static Status initBinaryTree(TreeNodePtr *t) {
    *t = NULL;
    return SUCCESS;;
}

/// 清空二叉树
static Status clearBinaryTree(TreeNodePtr *t) {
    if (*t) {
        // 递归释放左子树
        if ((*t)->lch) {
            clearBinaryTree(&(*t)->lch);
        }
        // 递归释放右子树
        if ((*t)->rch) {
            clearBinaryTree(&(*t)->rch);
        }
        // 释放自身节点
        free(*t);
        *t = NULL;
    }
    return SUCCESS;;
}

/// 判断为空
static int isEmptyBinaryTree(TreeNodePtr t) {
    if (t) {
        return 1;
    }
    return 0;
}

4.3 获取深度

/// 获取二叉树的深度
static int getBinaryTreeDepth(TreeNodePtr t) {
    if (!t) {
        return 0;;
    }
    // 左右子树的深度
    int lDepth = 0;
    int rDepth = 0;
    lDepth = getBinaryTreeDepth(t->lch);
    rDepth = getBinaryTreeDepth(t->rch);
    // 子树最大深度加一为自身深度
    int depth = (lDepth > rDepth ? lDepth : rDepth) + 1;
    return depth;
}

4.4 遍历

/// 前序遍历
static Status preOrderTraverse(TreeNodePtr t) {
    if (!t) {
        return ERROR;
    }
    // 1 打印自身结点
    printf("%d ", t->data);
    // 2 递归打印左结点
    preOrderTraverse(t->lch);
    // 3 递归打印右结点
    preOrderTraverse(t->rch);
    return SUCCESS;
}

/// 中序遍历
static Status inOrderTraverse(TreeNodePtr t) {
    if (!t) {
        return ERROR;
    }
    // 1 递归打印左结点
    inOrderTraverse(t->lch);
    // 2 打印自身结点
    printf("%d ", t->data);
    // 3 递归打印右结点
    inOrderTraverse(t->rch);
    return SUCCESS;
}

/// 后序遍历
static Status postOrderTraverse(TreeNodePtr t) {
    if (!t) {
        return ERROR;
    }
    // 1 递归打印左结点
    postOrderTraverse(t->lch);
    // 2 递归打印右结点
    postOrderTraverse(t->rch);
    // 3 打印自身结点
    printf("%d ", t->data);
    return SUCCESS;
}

4.5 使用

int main() {
    // 声明二叉树
    TreeNodePtr t;
    printf("初始化二叉树\n");
    initBinaryTree(&t);
    printf("构建二叉树\n");
    createBinaryTree(&t, 0, 10);
    
    printf(isEmptyBinaryTree(t) ? "二叉树为空\n" : "二叉树不为空\n");
    printf("二叉树的深度为 %d\n", getBinaryTreeDepth(t));
        
    printf("前序遍历：");
    preOrderTraverse(t);
    printf("\n");
    printf("中序遍历：");
    inOrderTraverse(t);
    printf("\n");
    printf("后序遍历：");
    postOrderTraverse(t);
    printf("\n");
    return 0;
}

打印结果：

初始化二叉树
构建二叉树
二叉树为空
二叉树的深度为 4
前序遍历：1 2 4 8 9 5 10 3 6 7 
中序遍历：8 4 9 2 10 5 1 6 3 7 
后序遍历：8 9 4 10 5 2 6 7 3 1