常见算法

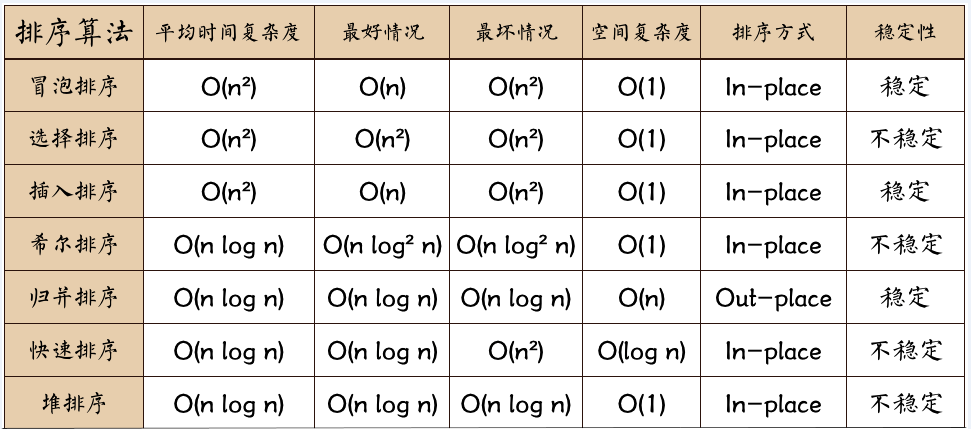
一、排序算法

1. 冒泡排序

（1）比较相邻的两个元素，如果前一个比后一个大，则交换位置。

（2）第一轮的时候最后一个元素应该是最大的一个。

（3）按照步骤一的方法进行相邻两个元素的比较，这个时候由于最后一个元素已经是最大的了，所以最后一个元素不用比较。

function bubbleSort(arr){
    for(let x=0;x<arr.length;x++){
        for(let y=0;y<arr.length-1;y++){
            if(arr[y]>arr[y+1]){
                [arr[y],arr[y+1]] = [arr[y+1],arr[y]]
            }
        }
    }
    return arr
}

2. 选择排序

（1）在未排序序列中找到最小元素，存放到排序序列的起始位置。

（2）再从剩余未排序元素中继续寻找最小元素，然后放到已排序序列的末尾。

function selectionSort(arr){
    for(let x = 0; x<arr.length; x++){
        let minIndex = x
        for(let y = x+1; y<arr.length; y++){
            if(arr[y]<arr[minIndex]){
                minIndex = y
            }
        }
        [arr[x],arr[minIndex]] = [arr[minIndex],arr[x]]
    }
    return arr
}

3. 插入排序

（1）假设数列第一个元素为已排序数列，剩余数列为未排序。

（2）将待排序元素挨个插入到已排序数列中每次插入都必须保证数列是有序的。

function insertSort(arr){
    for(let x=1; x<arr.length; x++){
        for(let y=x; y>0; y-- ){
            if(arr[y]<arr[y-1]){
                [arr[y-1],arr[y]] = [arr[y],arr[y-1]]
            }else{
                break
            }
        }
    }
    return arr
}

4. 希尔排序

（1）将整个待排序的列分割成为若干子序列

（2）分别进行直接插入排序

function ShellSort (arr) {
    const length = arr.length
    let gap = Math.floor(length)
    while (gap) {
        for (let i = gap; i < length; i++) {
            const temp = arr[i]
            let j
            for (j = i - gap; j >= 0 && temp < arr[j]; j = j - gap) {
                arr[j + gap] = arr[j]
            }
            arr[j + gap] = temp
        }
        gap = Math.floor(gap / 2)
    }
    return arr
}

5. 归并排序

将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

function mergeSort(arr){
    if(arr.length<2){
        return arr
    }
    let middle = parseInt(arr.length/2)
    let left = arr.slice(0,middle)
    let right = arr.slice(middle)
    function merge(left,right){
        let result = []
        while(left.length && right.length){
            if(left[0]<=right[0]){
                result.push(left.shift())
            }else{
                result.push(right.shift())
            }
        }
        while(left.length){
            result.push(left.shift())
        }
        while(right.length){
            result.push(right.shift())
        }
        return result
    }
    return merge(mergeSort(left), mergeSort(right))
}

6. 快速排序

快速排序是对冒泡排序的一种改进，第一趟排序时将数据分成两部分，一部分比另一部分的所有数据都要小。然后递归调用，在两边都实行快速排序。

var quickSort = function(arr) {
    if (arr.length < 2) {
        return arr
    }
    let middle = arr.splice(parseInt(arr.length / 2),1)[0]
    var left = []
    var right = []
    for (var i = 0; i < arr.length; i++){
        if (arr[i] < middle) {
            left.push(arr[i]);
        } else {
            right.push(arr[i]);
        }
    }
    return quickSort(left).concat([middle], quickSort(right));
}

7. 堆排序

function HeapSort (arr) {
    const length = arr.length

    // 调整初始堆，调整完其实也确定了最大值
    // 但此时最大值是在 arr[0] 中
    for (let i = Math.floor(length/2) - 1; i >= 0; i--) {
        adjustHeap(arr, i, length)
    }

    // 把 arr[0](最大值)换到后面
    for (let i = length - 1; i >=0; i--) {
        const temp = arr[0]
        arr[0] = arr[i]
        arr[i] = temp
        adjustHeap(arr, 0, i)
    }

    return arr
}

// size 是还需要调整的堆的大小
// 随着一个个最大值的确定，size 会越来越小
function adjustHeap (arr, position, size) {
    const left = position * 2 + 1
    const right = left + 1
    let maxIndex = position
    if (left < size && arr[left] > arr[maxIndex]) {
        maxIndex = left
    }
    if (right < size && arr[right] > arr[maxIndex]) {
        maxIndex = right
    }
    if (maxIndex !== position) {
        const temp = arr[position]
        arr[position] = arr[maxIndex]
        arr[maxIndex] = temp
        adjustHeap(arr, maxIndex, size)
    }
    return arr
}

二、查找算法

1. 顺序搜索

function sequentialSearch(arr,target){
    for(let i=0; i<item.length; i++){
        if(arr[i]===item){
            return i
        }
    }
    return -1
}

2. 二分搜索

function binarySearch(target,arr,start,end) {
    var start = start
    var end = end
    var mid = parseInt((start+end)/2)
    if(target === arr[mid]){
        return mid
    }else if(target > arr[mid]){
        return binarySearch(target,arr,mid+1,end)
    }else{
        return binarySearch(target,arr,start,mid-1)
    }
    return -1;
}