前言
本篇我们还要学习一个非线性的数据结构,虽然它是比较简单的,但是它是非常的重要的,我们接下来详细的学习它。篇幅过长,但请坚持读下去,会对你有帮助的。
定义和实现
树是一个非线性的数据结构,它在计算机科学中的各个领域被广泛使用,如文件系统就是树结构的,还有我们前端攻城狮最熟悉的HTML文档,还有我们最常用的域名体系,都是树结构。从它们的特征中我们可以总结出树是由父节点分叉连接子节点,就像自然界中的树一样。它分为树根和树枝,一棵树有一个总的树根,每个树根有多个树枝。一个树结构只有一个树根,而且没有子节点的节点叫做叶节点。这样一看是不是就和树一模一样呢?
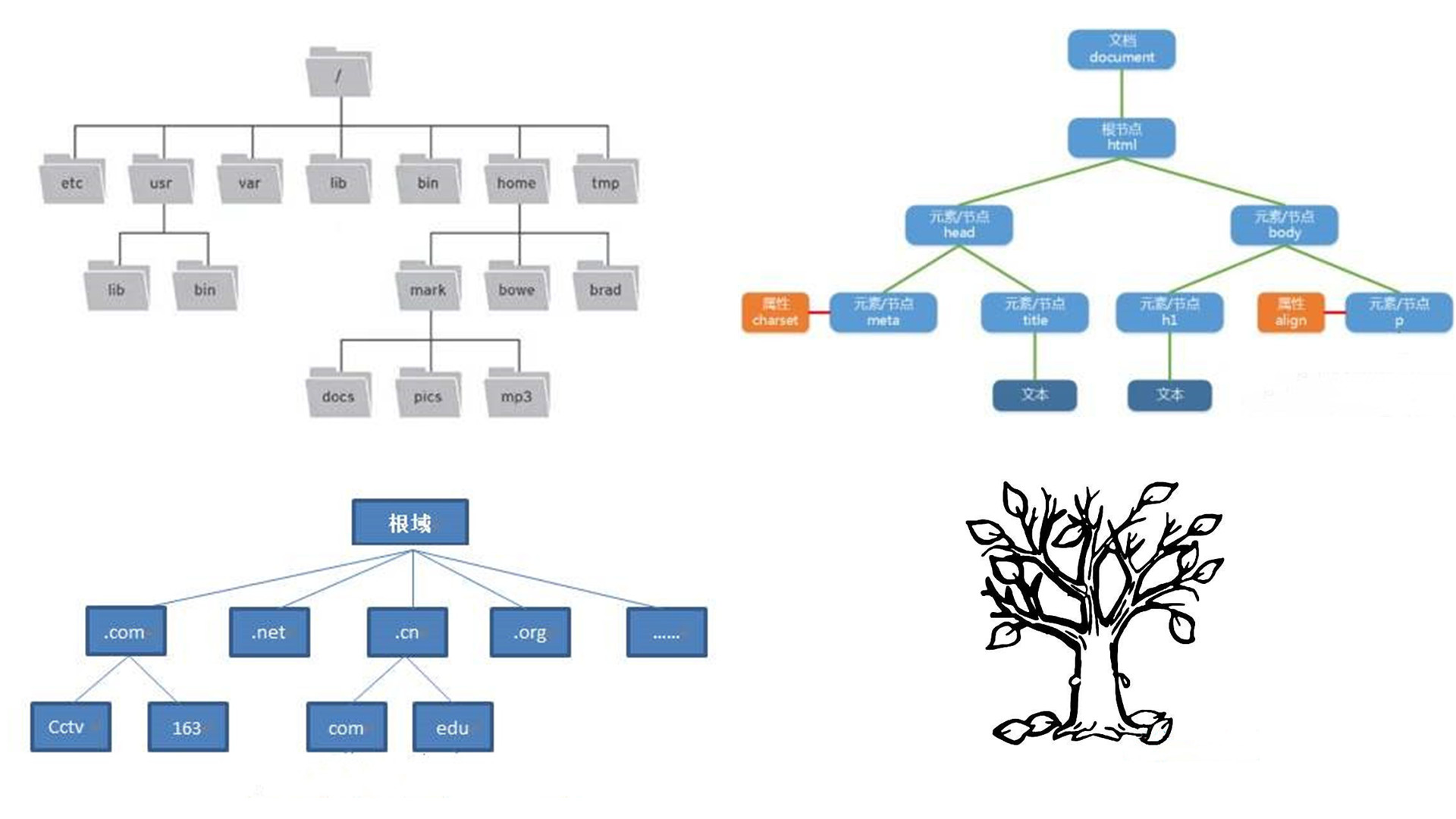
实现
通过图像更加理解了之后,我们用JavaScript代码来实现一下
//实现一个树结构
class Node {
constructor(value) {
this.key = value
this.left = null
this.right = null
}
insertLeft(value) {
if (this.left === null) {
this.left = new Node(value)
} else {
let t = new Node(value)
t.left = this.left
this.left = t
}
}
insertRight(value) {
if (this.right === null) {
this.right = new Node(value)
} else {
let t = new Node(value)
t.right = this.right
this.right = t
}
}
getRightChild() {
return this.right
}
getLeftChild() {
return this.left
}
setRootVal(value) {
this.key = value
}
getRootVal() {
return this.key
}
}
代码实现非常简单,也非常好理解。它借助了链表的思维,在每个节点中存储左右子节点的引用,配合着插入左右子树的操作,最后链接成一棵树。下面我们通过最简单的一种树——二叉树,来了解下树的遍历
树的遍历
树的遍历有三种方式
- 先序遍历
- 中序遍历
- 后序遍历
这其中的先中后说的其实就是访问父节点的次序,而左右子树都是遵循先访问左子树后访问右子树的顺序。所以先序遍历的顺序就是父->左子->右子、中序遍历的顺序就是左子->父->右子、后序遍历的顺序就是左子->右子->父。
每次需要访问一个节点之前都会先根据相应的规则去检测,拿中序遍历举个例子,每次访问一个节点,都会先检测这个节点是否有左子节点,如果有就去把目光移到左子节点,检测它是否有左子节点,以此类推,直到我们检测的节点没有左子节点,那就遍历它,然后再回过头来遍历它的父节点,最后遍历它的右子节点,目光到右子节点之后们也是这样进行检测之后再遍历。也许这里说的有点啰嗦,我们通过三幅图来感受一下具体的遍历步骤吧
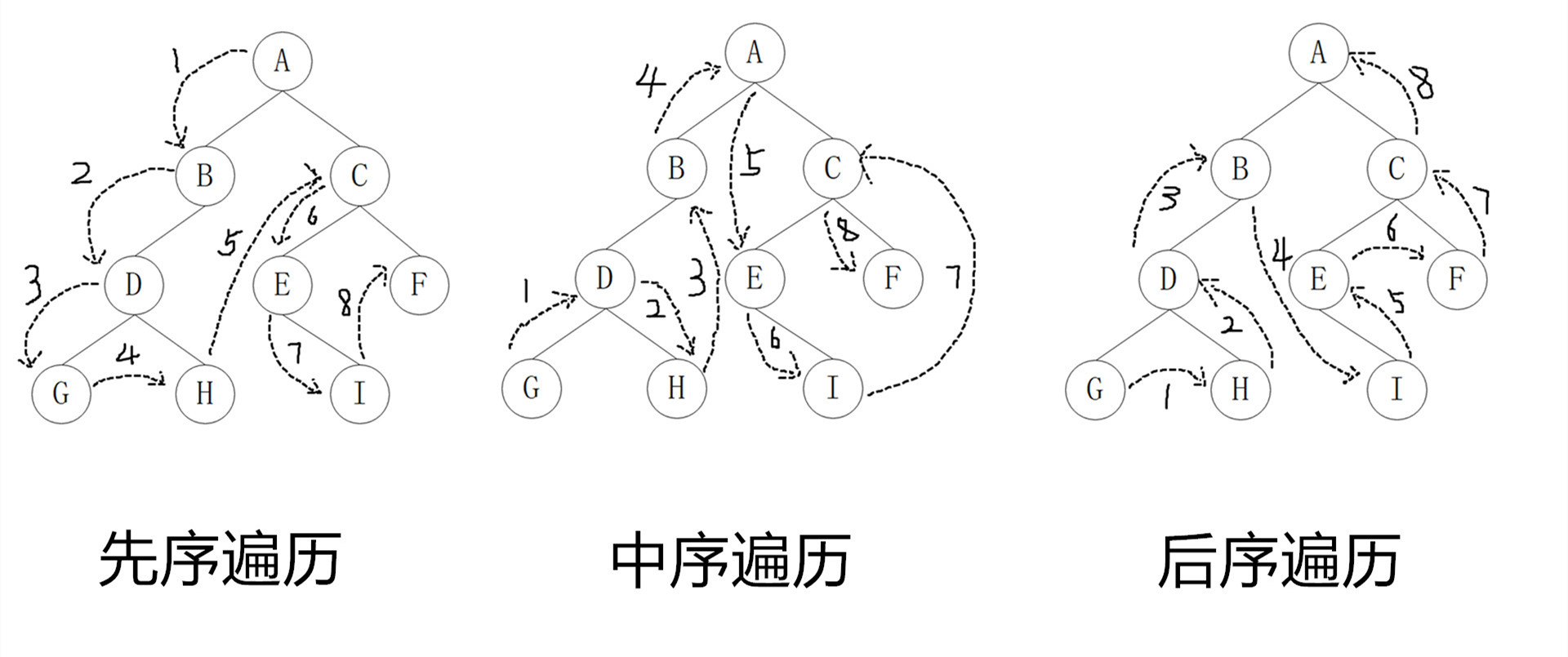
//先序遍历
function preorder(tree) {
if (!!tree) { // tree不为null也不为undefined
console.log(tree.getRootVal() + ' =>>')
preorder(tree.getLeftChild())
preorder(tree.getRightChild())
}
}
//中序遍历
function postorder(tree) {
if (!!tree) {
preorder(tree.getLeftChild())
console.log(tree.getRootVal() + ' =>>')
preorder(tree.getRightChild())
}
}
//后序遍历
function inorder(tree) {
if (!!tree) {
preorder(tree.getLeftChild())
preorder(tree.getRightChild())
console.log(tree.getRootVal() + ' =>>')
}
}
看到这里,是不是觉得树结构太简单了,不要太天真,我们后面可能要掌握非常复杂的树,做好心理准备,接下来我们慢慢的加大树的难度。
二叉堆
说起二叉堆我们要先直到优先队列这个东西,队列我们之前已经学过了,那么优先队列顾名思义就是有优先级的队列,会根据一定的规定来给队列中的数据进行排序,按顺序出队,我们先来简单的实现一下优先队列
class PriorityQueue {
constructor() {
this.items = [];
}
//加入一个元素到队列
enqueue (element) {
this.items.push(element);
}
//元素出队
dequeue () {
let priority = this.items[0].numbers;
let index = 0;
for (let i = 1;i < this.items.length;i++) {
if (this.items[i].numbers < priority) {
index = i;
}
}
return this.items.splice(index, 1);
}
//返回队列头元素
peek () {
if (this.isEmpty()) {
return undefined
}
return this.items[0];
}
//返回队列尾元素
getTail () {
if (this.isEmpty()) {
return undefined
}
return this.items[this.items.length - 1];
}
//判断队列是否为空
isEmpty () {
return this.items.length === 0
}
//返回数组中元素的个数
size () {
return this.items.length;
}
//元素是否存在于队列中
isInclude (key) {
return this.items.includes(key)
}
}
这里会在出队时根据元素的numbers来进行排序,决定谁先出队。我们的主角二叉堆和它的道理是差不多的,我们这将会了解到它。二叉堆是一个完全二叉树,完全二叉树通俗点说就是,只有最后一层和倒数第二层有叶节点,而且最后一层的叶节点一定在左部连续,而倒数第二层的叶节点一定在右部连续。这里还是放几个图吧,好理解一点。

class MinHeap {
constructor() {
//下标为0的项
this.heap = [0]
}
//向堆中插入新的值
insert(value) {
if (value != null) {
this.heap.push(value)
let index = this.heap.length - 1,
//获取父节点
parent = index === 0 ? undefined : Math.floor(index / 2)
//只要节点不是根节点,而且小于它的父节点则交换节点
while (
index > 1 &&
this.heap[parent] > this.heap[index]
) {
let temp = this.heap[index]
this.heap[index] = this.heap[parent]
this.heap[parent] = temp
index = parent
parent =
index === 0 ? undefined : Math.floor(index / 2)
}
return true
}
return false
}
//返回堆的大小
size() {
return this.heap.length - 1
}
//堆是否为空
isEmpty() {
return this.heap.length === 1
}
//查找堆的最小值
findMin() {
return this.isEmpty() ? undefined : this.heap[1]
}
//移除最小值
delMin() {
if (this.isEmpty()) {
return undefined
}
//如果只有一个节点则没必要再组合
if (this.heap.length === 2) {
return this.heap.splice(1,1)
}
const removedValue = this.heap.splice(1,1)
this.swapDown(1)
return removedValue
}
//下移操作
swapDown(index) {
let element = index
const left = 2 * index
const right = 2 * index + 1
const size = this.size()
//如果左子节点大于当前节点
if (left < size && this.heap[left] < this.heap[index]) {
element = left
}
//如果右子节点大于当前节点
if (right < size && this.heap[right] < this.heap[index]) {
element = right
}
//如果当前节点有比它大的子节点,那就交换
if (index !== element) {
let temp = this.heap[index]
this.heap[index] = this.heap[element]
this.heap[element] = temp
this.swapDown(element)
}
}
}
这里只实现了最小堆,0下标处弃掉不用,这样在计算下标时比较清晰。插入和删除时的整理操作稍微有些复杂,但是仔细研究一下就能看懂。看懂之后可以自己实现一下最大堆,收获满满的成就感。
二叉查找树
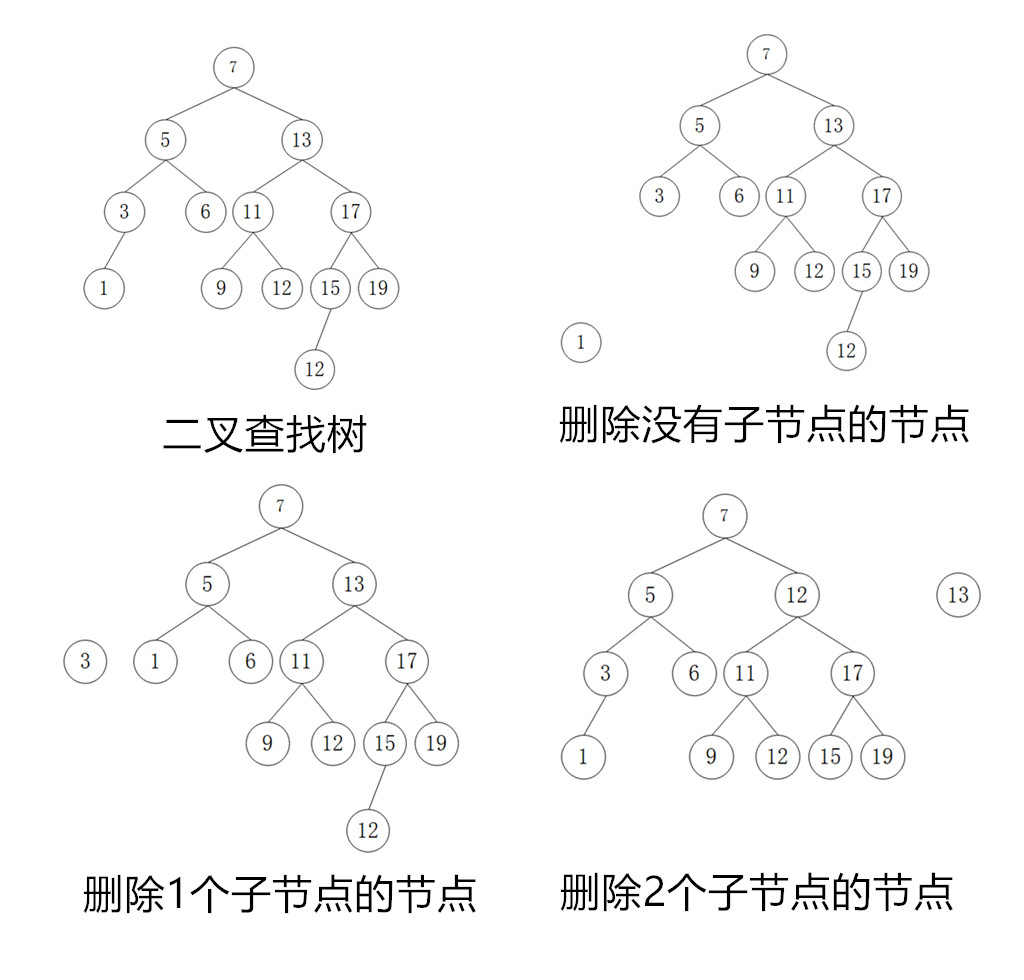
二叉查找树(Binary Search Tree)就是我们常说的BST,它也是在二叉树的基础上进行了限制,每个节点的左子节点需要小于它,而右子节点需要大于它。也是很好理解哈。它的插入操作是比较好实现了,比较困难的是它的删除操作。删除一个节点后,也要保证BST保持相应的性质,它分为三种情况
- 这个节点没有子节点
- 这个节点有1个子节点
- 这个节点有2个子节点
第一种情况是比较容易的,直接删除掉就行了;第二种情况也还行,就将唯一的这个子节点上移代替它就行了;最困难的是第三种情况,当它有两个节点的时候没有办法简单的上移哪个节点,于是我们就找一个节点来替代它,那么是怎么找呢,就找右子树的最小的节点,也就是右子树的最左边的左节点。我们还是放一个图会更清晰些。
class BinarySearchTree {
constructor() {
this.root = null
}
insert(key) {
if (this.root === null) {
this.root = new Node(key)
} else {
this.insertNode(this.root, key)
}
}
insertNode(node, key) {
//如果小于当前节点则向左子树查询
if (node.key > key) {
if (node.left == null) {
node.left = new Node(key)
} else {
this.insertNode(node.left, key)
}
} else {
if (node.right == null) {
node.right = new Node(key)
} else {
this.insertNode(node.right, key)
}
}
}
min() {
return this.minNode(this.root)
}
minNode(node) {
let current = node
//循环直到找到最左的左子节点
while (current != null && current.left != null) {
current = current.left
}
return current
}
max() {
return this.maxNode(this.root)
}
maxNode() {
let current = node
//循环直到找到最右的右子节点
while (current != null && current.right != null) {
current = current.right
}
return current
}
search(key) {
return this.searchNode(this.root,key)
}
searchNode(node,key) {
if (node == null) {
return false
}
//判断小于当前节点则向左查找大于当前节点则向右查找
if (node.key > key) {
return this.searchNode(node.left, key)
} else if (this.root.key < key) {
return this.searchNode(node.right, key)
} else {
return true
}
}
remove(key) {
this.root = this.removeNode(this.root, key)
}
removeNode(node, key) {
if (node == null) {
return null
}
if (node.key > key) {
node.left = this.removeNode(node.left, key)
//需要返回值去移除父节点中对被移除的子节点的引用
return node
} else if (node.key < key) {
node.right = this.removeNode(node.right, key)
return node
} else {
//第一种情况 没有子节点
if (node.left == null && node.right == null) {
node = null
return node
}
//第二种情况 有一个子节点
if (node.left == null) {
node = node.right
return node
} else if (node.right == null) {
node = node.left
return node
}
//第三种情况 有两个子节点
const replaceNode = this.minNode(node.right) //取出其右子树的最小值来替代它
//修改键的值
node.key = replaceNode.key
node.right = this.removeNode(
node.right,
replaceNode.key
)
//移除右子树中最小值的键
return node
}
}
}
用代码实现之后,是不是更加清晰了呢,如果还有些疑惑的话,自己实现一遍,困难就迎刃而解啦。二叉查找树的时间复杂度可以达到O(logn),这已经是效率很高了,但是如果出现极端情况,也就是像每个节点都只有右子节点、每个节点都只有左子节点,这样就相当于是线性链表结构了,时间复杂度就变成了O(n),这也就是二叉查找树的缺陷了,为了解决这个缺陷,自平衡二叉树便登场了。
AVL树
在讲AVL树之前,我们需要再了解一些树的基础知识。树的层级——从根节点开始到达一个节点的路径所包含的边的数量。树的高度——树中所有节点的最大层级。平衡因子——左子树的高度-右子树的高度。了解了这些知识之后,我们就可以介绍平衡二叉树了,即如果一个二叉查找树中每个节点的平衡因子都在-1、0、1之间,那么这个二叉树就叫做平衡二叉树。自然自平衡二叉树就是如果不平衡会自己自动平衡。AVL就是自平衡二叉树的一种,注意,AVL不是什么高端的名词,而是三个人的人名Adelson-Velskii-Landi。AVL树的难点就在于树的平衡了。有两种不平衡的情况出现,即左重和右重。
左重也就是节点的平衡因子大于1,这个时候就进行右旋转,右旋转就是将它的左子节点作为它的父节点,而它作为它左子节点的右子节点,如果它的左子节点有右子节点,就将这个右子节点作为它的左子节点。右重则相反,进行左旋转,左旋转就是将它的右子节点作为它的父节点,而它作为它右子节点的左子节点,如果它的右子节点有左子节点,就将这个左子节点作为它的右子节点。说的有点绕,我们看一个图就明白了
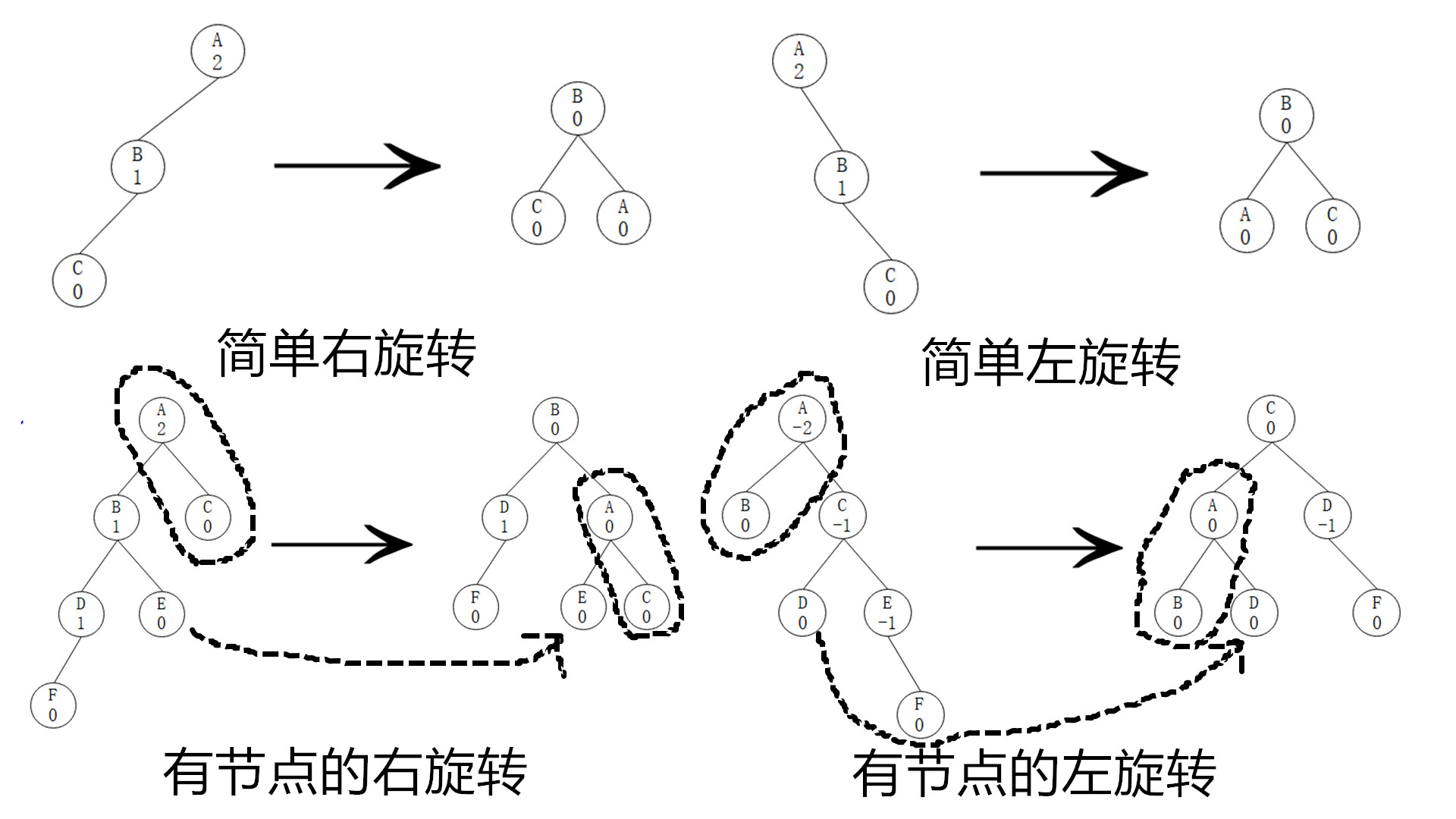
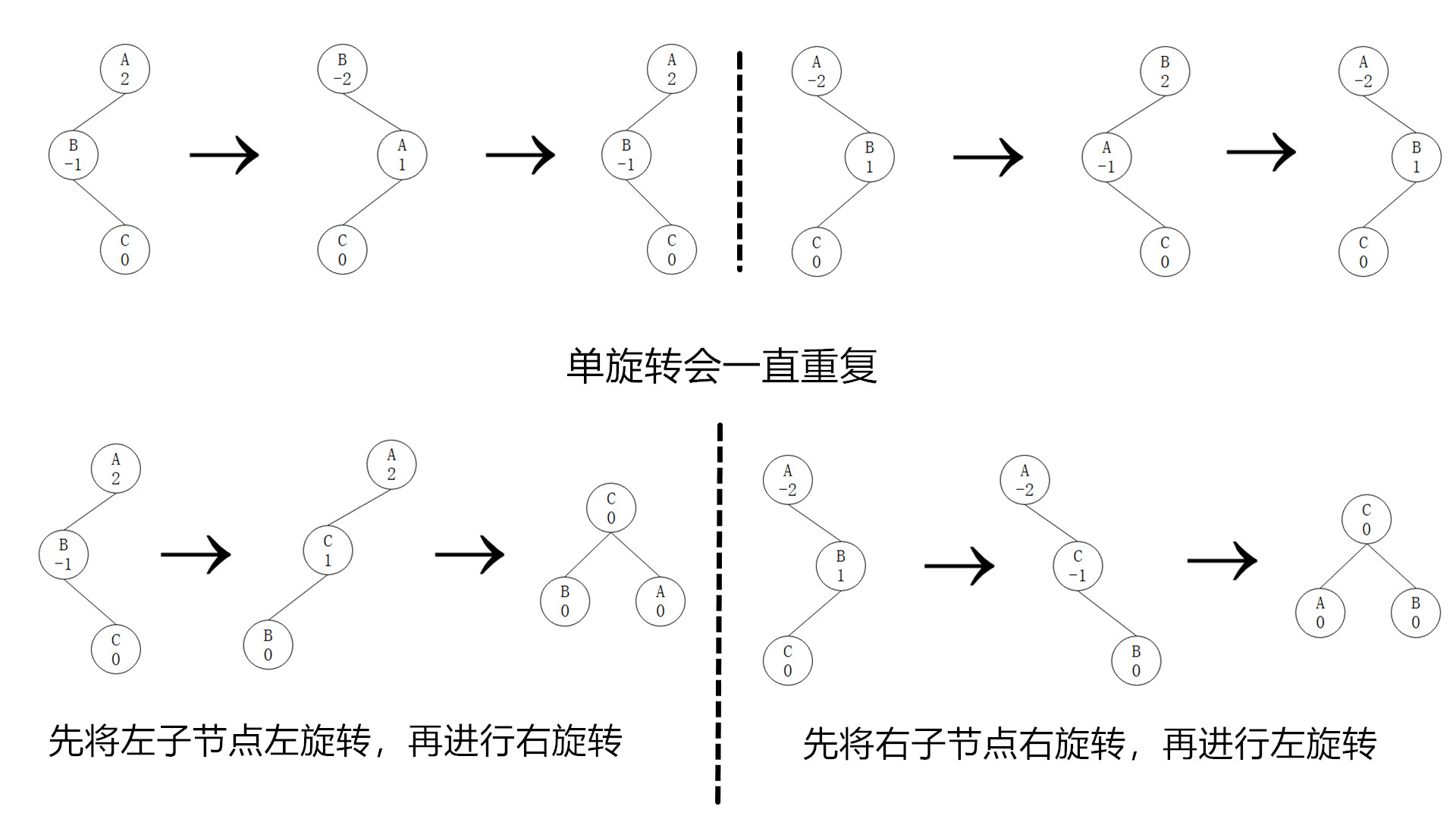
class AVLNode extends Node {
constructor(key, parent) {
super(key);
this.parent = null;
}
}
class AVLTree extends BinarySearchTree {
constructor() {
super()
this.root = null;
}
//获取树的高度
getNodeHeight(node) {
if (node == null) {
return -1;
}
//递归调用子树高度+1
return Math.max(this.getNodeHeight(node.left), this.getNodeHeight(node.right)) + 1;
}
//计算一个节点的平衡因子
getBalanceFactor(node) {
return this.getNodeHeight(node.left) - this.getNodeHeight(node.right);
}
//左旋转
leftRotation(node) {
//取出它的右节点
let newNode = node.right
//判断当前节点是父节点的哪个节点或者是否有父节点,并相对将取出的节点替换他
if (node.parent == null) {
newNode.parent = null
this.root = newNode
} else if (node.parent.right === node) {
node.parent.right = newNode
newNode.parent = node.parent
} else {
node.parent.left = newNode
newNode.parent = node.parent
}
//判断取出的节点是否有左子节点,如果有就把它挂到当前节点的右节点,否则将当前节点的右节点置为null
if (newNode.left !== null) {
node.right = newNode.left
newNode.left.parent = node
} else {
node.right = null
}
//建立他俩的新关系,也就是旋转
newNode.left = node
node.parent = newNode
}
//右旋转
//与左旋转逻辑类似
rightRotation(node) {
let newNode = node.left
if (node.parent == null) {
newNode.parent = null
this.root = newNode
} else if (node.parent.right === node) {
node.parent.right = newNode
newNode.parent = node.parent
} else {
node.parent.left = newNode
newNode.parent = node.parent
}
if (newNode.right !== null) {
node.left = newNode.right
newNode.right.parent = node
} else {
node.left = null
}
newNode.right = node
node.parent = newNode
}
//向平衡树中插入节点
insert(key) {
if (this.root === null) {
this.root = new AVLNode(key)
} else {
this.insertNode(this.root, key)
}
}
insertNode(node, key) {
if (key < node.key) {
if (node.left !== null) {
this.insertNode(node.left, key)
} else {
node.left = new AVLNode(key, node)
//存储父节点
node.left.parent = node
//平衡节点
this.updateBalance(node.left)
}
} else {
if (node.right !== null) {
this.insertNode(node.right, key)
} else {
node.right = new AVLNode(key, node)
node.right.parent = node
this.updateBalance(node.right)
}
}
return node;
}
//平衡节点的函数
updateBalance(node) {
//获取平衡因子
const balanceFactor = this.getBalanceFactor(node);
//左子树不平衡
if (balanceFactor > 1) {
//判断其左子树是否右重(也就是更复杂的情况)
if (this.getBalanceFactor(node.left) < 0) {
this.leftRotation(node.left)
}
this.rightRotation(node)
}
//右子树不平衡
if (balanceFactor < -1) {
if (this.getBalanceFactor(node.right) > 0) {
this.rightRotation(node.right)
}
this.leftRotation(node)
}
//如果父节点存在则递归进行检查平衡
if (node.parent !== null) {
this.updateBalance(node.parent)
}
}
remove(key) {
this.removeNode(this.root, key)
}
removeNode(node, key) {
//判断它是大于还是小于当前节点,进一步去子树中删除
if (node.key > key) {
this.removeNode(node.left, key)
} else if (node.key < key) {
this.removeNode(node.right, key)
} else {
//第一种情况 没有子节点
if (node.left == null && node.right == null) {
//根节点 直接制空树,根据它是父节点的哪个节点进行修改
if (node.parent == null) {
this.root = null
} else if (node.parent.right === node) {
node.parent.right = null
} else {
node.parent.left = null
}
} else if (node.left == null) {//第二种情况 有一个子节点
//将值替换并删除子节点
node.key = node.right.key
node.right = null
} else if (node.right == null) {
node.key = node.left.key
node.left = null
} else {//第三种情况 有两个子节点
//取出其右子树的最小值来替代它
const replaceNode = this.minNode(node.right)
//修改键的值
node.key = replaceNode.key
//修改子树中的这个值
this.removeNode(
node.right,
replaceNode.key
)
}
}
this.updateBalance(node)
}
print() {
this.printTree(this.root)
}
//用来测试树结构
printTree(node) {
if (node === this.root) {
console.log(node.key)
}
if (node.left !== null) {
console.log(node.key + " left=>" + node.left.key)
this.printTree(node.left)
}
if (node.right !== null) {
console.log(node.key + " right=>" + node.right.key)
this.printTree(node.right)
}
}
}
这里需要将继承NODE类,因为我们需要存储每个节点的父节点。注释给的比较详细,这里特意把代码写的详细简单些,更有助于理解这个复杂的东西,可能代码有点长,不过静下心来看肯定能看懂,逻辑是比较清晰的。如果你理解了这堆代码并能够自己写出来,那么说明你已经很厉害了,如果还心有余力的话,我们继续进击红黑树。
红黑树
红黑树也是自平衡树的一种,它也经常出现在面试中,所以即使它很困难,我们也非常有必要去学习它。红黑树最重要就是这些支撑它的规则:
- 顾名思义,每个节点不是红色的就是黑色的。
- 树的根节点永远是黑色
- 所有叶节点都是黑色的,它们都是NULL来表示
- 红色的节点的两个子节点都是黑色的,红色的节点不能相邻,也就说红色节点的父节点和子节点都必须为黑色
- 从当前节点到它的叶节点(也就是NULL)的所有路径中都包含相同数量的黑色节点
把这些规则罗列起来一看都很简单哈,非常好理解,红黑树的平衡全靠它。那么它的难点在哪呢,也许你已经猜到了,就是在插入和移除节点的时候可能需要调整节点的位置或者颜色。接下来我们就仔细研究一下它们。
插入操作
每一个插入的节点都应该是红色的,因为这样就不会在插入的时候影响到规则5。当插入的节点的父节点是黑色的,那将是最好的情况,不会影响树的平衡。在这个前提下,如果父节点也是红色,那么将会影响规则4,这时我们将要平衡它,我们有两种平衡方式,即变色和旋转。
变色
如果插入节点的父节点为红色,而且它的叔节点也为红色,那么我们就可以通过依次改变它们的颜色来保持树的平衡,具体改动如图
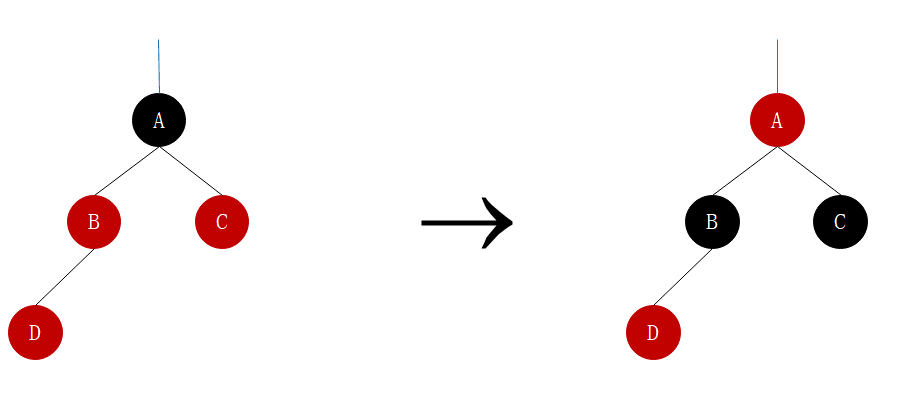
旋转
如果插入节点的父节点为红色,而且它的叔节点为黑色或者没有叔节点(为null)则需要旋转才能解决问题了,旋转也像AVL树一样,有四种旋转的情况。
- 如果作为左子节点插入到父节点,而且父节点也是祖父节点的左子节点则需要进行右旋转;
- 如果作为右子节点插入到父节点,而且父节点也是祖父节点的左子节点则需要先进行左旋转再右旋转;
- 如果作为右子节点插入到父节点,而且父节点也是祖父节点的右子节点则需要进行左旋转;
- 如果作为左子节点插入到父节点,而且父节点也是祖父节点的右子节点则需要先进行右旋转再左旋转;
这里具体的旋转方法不再赘述,放一个图来小小的感受下吧
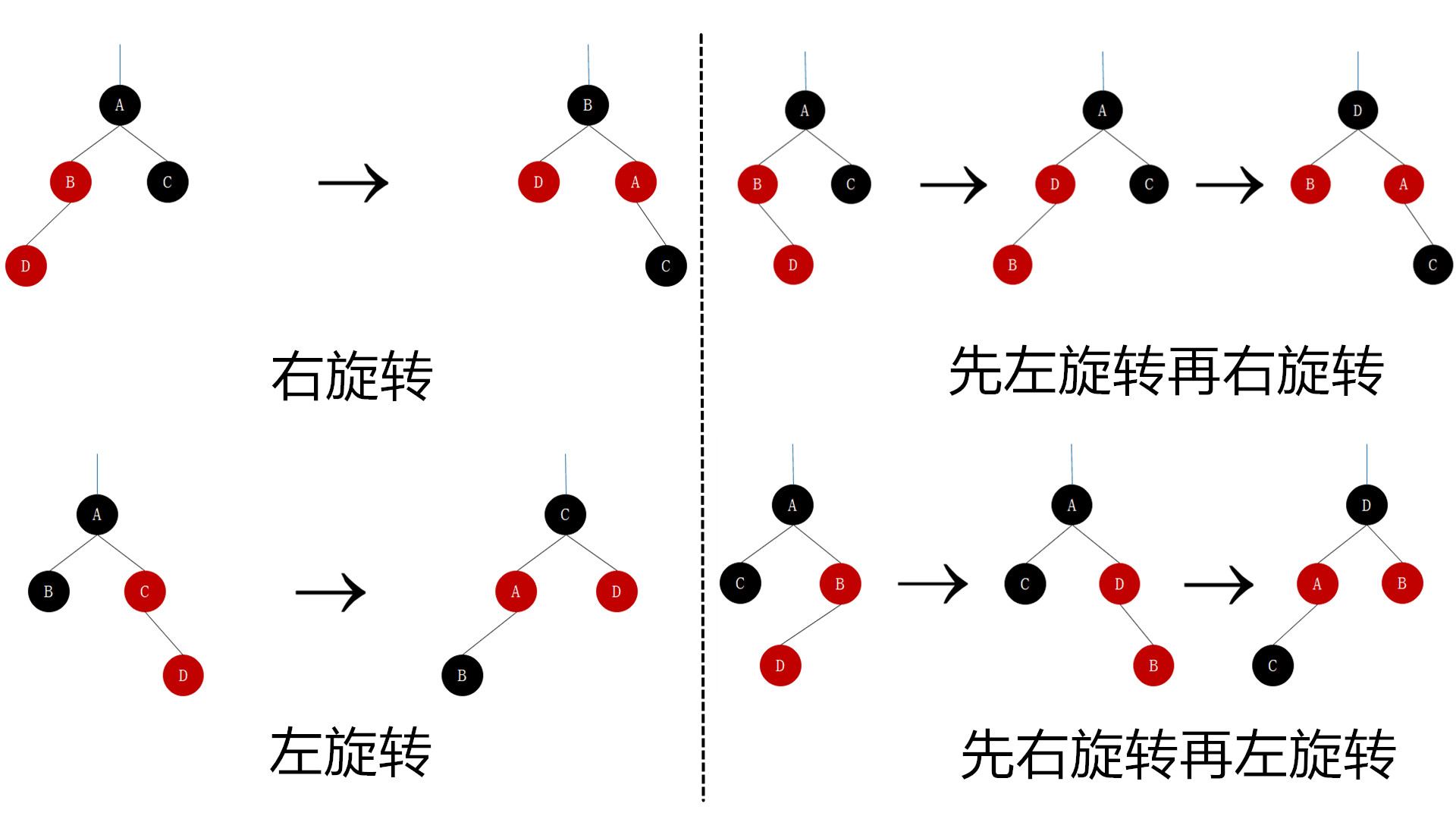
删除操作
插入操作说完之后,我们还要细讲一下删除操作
因为它的规则限制,和二叉搜索树的删除情况还是有些不同的,有一些情况是一定不会发生的,因为规则5的约束,不会出现节点的一个子节点为黑色,另一个子节点为空、的情况。因为规则4的约束,也不会出现当前节点为红色,子节点也为红色的情况。知道这些之后,我们将详细讨论其他情况
- 1 如果删除的节点为红色
- 1.1 删除的节点为叶节点
这样直接删除该节点就可以,不会影响红黑树的平衡 - 1.2 删除的节点只有一个节点
此情况不可能发生,因为红色节点的子节点只能是黑色的,而上面已经说过这种情况下不可能发生
- 1.1 删除的节点为叶节点
- 2 如果删除的节点为黑色
- 2.1 如果删除的节点是叶节点
- 2.1.1 删除节点的兄弟节点为红色
- a. 删除节点是父节点的左子节点
这样会违反规则5,我们将其父节点左旋转,然后将父节点颜色改为红色,兄弟节点改为黑色,这样我们就变成了2.1.2的情况 - b. 删除节点是父节点的右子节点
和上一个类似,将其父节点右旋转,然后将父节点颜色改为红色,兄弟节点改为黑色,这样我们就变成了2.1.2的情况
- a. 删除节点是父节点的左子节点
- 2.1.2 删除节点的兄弟节点为黑色
- a. 兄弟节点的离删除节点远的子节点为红色
- ① 删除节点为父节点的左子节点
此时兄弟节点的离删除节点远的子节点为其兄弟节点的右子节点,需要将其父节点和兄弟节点的颜色进行交换,然后再将父节点进行左旋转操作,最后将兄弟节点的离删除节点远的子节点置为黑色 - ② 删除节点为父节点的右子节点
此时兄弟节点的离删除节点远的子节点为其兄弟节点的左子节点,和上面的类似,将其父节点和兄弟节点的颜色进行交换,然后再将父节点进行右旋转操作,最后将兄弟节点的离删除节点远的子节点置为黑色
- ① 删除节点为父节点的左子节点
- b. 兄弟节点仅有的离删除节点近的子节点为红色
- ① 删除节点为父节点的左子节点
此时兄弟节点的离删除节点近的子节点为其兄弟节点的左子节点,这时就需要先将兄弟节点右旋并交换其和左子节点的颜色,然后再将父节点左旋,交换父节点和兄弟节点的颜色,也就是AVL里的先右旋再左旋操作 - ② 删除节点为父节点的右子节点
此时兄弟节点的离删除节点近的子节点为其兄弟节点的右子节点,和上面类似,先将兄弟节点左旋并交换其和右子节点的颜色,然后再将父节点右旋,交换父节点和兄弟节点的颜色,也就是AVL里的先左旋再右旋操作
- ① 删除节点为父节点的左子节点
- c. 兄弟节点为叶节点
- ① 删除节点的父节点为红色
此时删除后会违反规则5,我们就需要将其父节点改为黑色,并把其兄弟节点改为红色 - ② 删除节点的父节点为黑色
此时删除后也会违反规则5,我们将其兄弟节点改成红色就行了
- ① 删除节点的父节点为红色
- a. 兄弟节点的离删除节点远的子节点为红色
- 2.1.1 删除节点的兄弟节点为红色
- 2.2 如果删除的节点只有左子树或者右子树,这时候它独有的子节点只能是红色的,上面说过不可能出现单个黑色子节点
这种情况下直接拿他的子节点来代替,并且改成黑色就好了。
- 2.1 如果删除的节点是叶节点
这里只讨论了叶节点和只有一个节点的情况,因为两个节点的删除,本质上也是找一个后继来替代他,然后删掉这个后继,也就是还是回归到了前两种情况。原理明白了之后,我们动手用JavaScript代码来实现它,因为它也是二叉查找树,所以我们只需要重写插入和删除方法即可
class RedBlackNode extends Node {
constructor(key) {
super(key);
this.key = key;
this.color = 'red';
this.parent = null;
}
}
class RedBlackTree extends BinarySearchTree {
constructor() {
super();
this.root = null;
}
//获取树的高度
getNodeHeight(node) {
if (node == null) {
return -1;
}
//递归调用子树高度+1
return Math.max(this.getNodeHeight(node.left), this.getNodeHeight(node.right)) + 1;
}
//计算一个节点的平衡因子
getBalanceFactor(node) {
return this.getNodeHeight(node.left) - this.getNodeHeight(node.right);
}
minNode(node) {
let current = node
//循环直到找到最左的左子节点
while (current != null && current.left != null) {
current = current.left
}
return current
}
//左旋转
leftRotation(node) {
//取出它的右节点
let newNode = node.right
//判断当前节点是父节点的哪个节点或者是否有父节点,并相对将取出的节点替换他
if (node.parent == null) {
newNode.parent = null
this.root = newNode
} else if (node.parent.right === node) {
node.parent.right = newNode
newNode.parent = node.parent
} else {
node.parent.left = newNode
newNode.parent = node.parent
}
//判断取出的节点是否有左子节点,如果有就把它挂到当前节点的右节点,否则将当前节点的右节点置为null
if (newNode.left !== null) {
node.right = newNode.left
newNode.left.parent = node
} else {
node.right = null
}
//建立他俩的新关系,也就是旋转
newNode.left = node
node.parent = newNode
}
//右旋转
//与左旋转逻辑类似
rightRotation(node) {
let newNode = node.left
if (node.parent == null) {
newNode.parent = null
this.root = newNode
} else if (node.parent.right === node) {
node.parent.right = newNode
newNode.parent = node.parent
} else {
node.parent.left = newNode
newNode.parent = node.parent
}
if (newNode.right !== null) {
node.left = newNode.right
newNode.right.parent = node
} else {
node.left = null
}
newNode.right = node
node.parent = newNode
}
//插入元素
insert(key) {
if (this.root == null) {
this.root = new RedBlackNode(key);
this.root.color = 'black';
} else {
this.insertNode(this.root, key);
}
}
insertNode(node, key) {
if (key < node.key) {
if (node.left !== null) {
this.insertNode(node.left, key)
} else {
node.left = new RedBlackNode(key, node)
//存储父节点
node.left.parent = node
//平衡节点
this.adjustNodes(node.left)
}
} else {
if (node.right !== null) {
this.insertNode(node.right, key)
} else {
node.right = new RedBlackNode(key, node)
node.right.parent = node
this.adjustNodes(node.right)
}
}
}
//填色
adjustNodes(node) {
//node的父节点不为空,而且它的父节点为红色
while (node.parent !== null && node.parent.color === 'red') {
let parent = node.parent;
const grandParent = parent.parent;
//父节点是祖父节点的左子节点
if (grandParent !== null && grandParent.left === parent) {
const uncle = grandParent.right;
//叔节点也是红色 那么只需要重新填色
if (uncle !== null && uncle.color === 'red') {
grandParent.color = 'red';
parent.color = 'black';
uncle.color = 'black';
node = grandParent;
} else { //叔节点为黑色
//如果插入的节点是其父节点的左子节点
if (node === parent.left) {
this.rightRotation(grandParent)
parent.color = 'black'
grandParent.color = 'red'
node = parent
} else {//如果插入的节点是其父节点的右子节点
this.leftRotation(parent)
this.rightRotation(grandParent)
node.color = 'black'
grandParent.color = 'red'
}
}
} else { //父节点是祖父节点的右子节点
const uncle = grandParent.left;
//叔节点是红色则只需要重新填色
if (uncle !== null && uncle.color === 'red') {
grandParent.color = 'red';
parent.color = 'black';
uncle.color = 'black';
node = grandParent;
} else { // 叔节点为黑色
//如果插入的节点是其父节点的右子节点
if (node === parent.right) {
this.leftRotation(grandParent);
parent.color = 'black'
grandParent.color = 'red'
node = parent;
} else {//如果插入的节点是其父节点的左子节点
this.rightRotation(parent)
this.leftRotation(grandParent);
node.color = 'black';
grandParent.color = 'red';
}
}
}
}
this.root.color = 'black';
}
/**
remove(key) {
this.removeNode(this.root, key)
}
/** 实现的具体逻辑
* - 删除的节点为黑色
* - 删除的节点为叶节点
* - 删除节点是父节点的左子节点
* - 删除节点的兄弟节点为红色
* - 删除节点的兄弟节点为黑色
* - 兄弟节点的离删除节点远的子节点为红色
* - 兄弟节点的离删除节点近的子节点为红色
* - 兄弟节点为叶节点
* - 父节点为红色
* - 父节点为黑色
* - 删除节点是父节点的右子节点
* - 删除节点的兄弟节点为红色
* - 删除节点的兄弟节点为黑色
* - 兄弟节点的离删除节点远的子节点为红色
* - 兄弟节点的离删除节点近的子节点为红色
* - 兄弟节点为叶节点
* - 父节点为红色
* - 父节点为黑色
* - 删除的节点只有一个子节点
* - 删除的节点有两个子节点
* - 删除的节点为红色
* - 删除的节点为叶节点
* - 删除的节点有两个子节点
*/
removeNode(node, key) {
//判断它是大于还是小于当前节点,进一步去子树中删除
if (node.key > key) {
this.removeNode(node.left, key)
} else if (node.key < key) {
this.removeNode(node.right, key)
} else {
//节点颜色为红色
if (node.color === 'red') {
//红色叶节点直接删除
if (node.left == null && node.right == null) {
//根节点 直接制空树,根据它是父节点的哪个节点进行修改
if (node.parent == null) {
this.root = null
} else if (node.parent.right === node) {
node.parent.right = null
} else {
node.parent.left = null
}
} else { //有两个子节点
//取出其右子树的最小值来替代它
const replaceNode = this.minNode(node.right)
//修改键的值
node.key = replaceNode.key
//直接改为删除替换的那个节点
this.removeNode(
node.right,
replaceNode.key
)
}
} else { //节点颜色为黑色
//第一种情况 没有子节点
if (node.left == null && node.right == null) {
//保存父节点的引用
let parent = node.parent
//根节点 直接制空树,根据它是父节点的哪个节点进行修改
if (parent == null) {
this.root = null
} else if (parent.left === node) { //父节点的左子节点
//删除该节点
parent.left = null
//保存兄弟节点
let brother = parent.right
//兄弟节点为红色,先处理一下,再进入黑色处理
if (brother !== null && brother.color === 'red') {
this.leftRotation(parent)
parent.color = 'red'
brother.color = 'black'
}
// 兄弟节点为黑色
let distantNephew = brother.right,
nearNephew = brother.left
//兄弟节点的离删除节点远的子节点为红色
if (distantNephew !== null && distantNephew.color === 'red') {
this.leftRotation(parent)
const temp = parent.color
parent.color = brother.color
brother.color = temp
distantNephew.color = 'black'
} else if (distantNephew == null && nearNephew == null) {// 兄弟节点为叶节点
if (parent.color === 'red') {
parent.color = 'black'
brother.color = 'red'
} else {
brother.color = 'red'
}
} else { //兄弟节点仅有的离删除节点近的子节点为红色
this.rightRotation(brother)
this.leftRotation(parent)
const temp = parent.color
parent.color = brother.color
brother.color = temp
distantNephew.color = 'black'
}
} else {
parent.right = null
//保存兄弟节点
let brother = parent.left
if (brother !== null && brother.color === 'red') {
parent.right = null
this.rightRotation(parent)
parent.color = 'red'
brother.color = 'black'
}
let distantNephew = brother.left,
nearNephew = brother.right
if (distantNephew !== null && distantNephew.color === 'red') {
this.rightRotation(parent)
const temp = parent.color
parent.color = brother.color
brother.color = temp
distantNephew.color = 'black'
} else if (distantNephew == null && nearNephew == null) {
if (parent.color === 'red') {
parent.color = 'black'
brother.color = 'red'
} else {
brother.color = 'red'
}
} else {
this.leftRotation(brother)
this.rightRotation(parent)
const temp = parent.color
parent.color = brother.color
brother.color = temp
distantNephew.color = 'black'
}
}
} else if (node.left == null) {//第二种情况 有一个子节点
//将值替换并删除子节点
node.key = node.right.key
node.right = null
} else if (node.right == null) {
node.key = node.left.key
node.left = null
} else {//第三种情况 有两个子节点
//取出其右子树的最小值来替代它
const replaceNode = this.minNode(node.right)
//修改键的值
node.key = replaceNode.key
//删除子树中的这个值
this.removeNode(
node.right,
replaceNode.key
)
}
}
}
}
print() {
this.printTree(this.root)
}
//用来测试树结构
printTree(node) {
console.log(node)
if (node === this.root) {
console.log(node.key)
}
if (node.left !== null) {
console.log(node.key + "(" + node.color + ") left=>" + node.left.key)
this.printTree(node.left)
}
if (node.right !== null) {
console.log(node.key + "(" + node.color + ") right=>" + node.right.key)
this.printTree(node.right)
}
}
}
我们还是要继承Node类来创建RedBlackNode类,因为我们需要存储颜色和父节点的引用。这里的代码和AVL树一样,也是尽量写的简单、详细,便于理解一些。所以建议读者去自己实现一下,哪里不会了再回来看,只有自己真正的实现一下,体会才会更深。学到这里我们已经学会了树的大部分知识,如果觉得意犹未尽可以自己再去学习B树、B+树,它们是更加复杂的树,在这里就不去介绍了。上面的这些都掌握的话就已经很棒了。
小结
本篇文章篇幅过长,因为想尽量讲的详细些,通俗易懂些。图都是自己画的,代码纯手打。如果觉得对你有帮助或者真的学到东西了,可以给一个小赞作为鼓励。如果有什么表达不当或者其他错误请尽管指出,让我们一起进步,加油!!!