KMP 是由 D.E.Knuth,J.H.Morrs 和 VR.Pratt。发表的一个模式匹配算法,可以大大避免重复遍历的情况。
KMP模式匹配算法原理
我们拿上一篇中的 BF 算法,与 KMP 算法实现过程分析做对比说明。
假如有题目一:
假如现在有一个主串 S = "abcdefgabed",模式串 T = "abcdex",找出T 在 S 中完全匹配时的首地址。
BF 算法执行流程
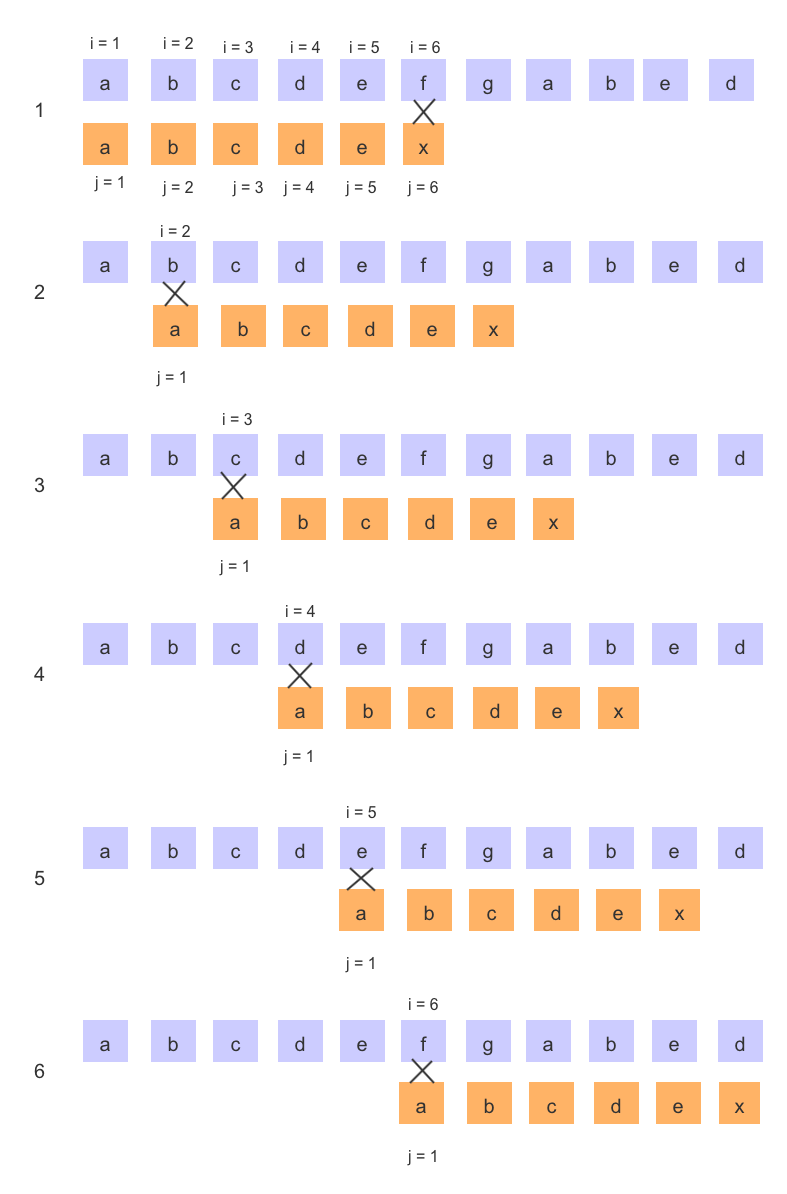
上图便是BF算法的执行过程,并由此可以得出,当在模串"abcdex"中 字符'a' 是唯一存在的情况下,经过第一轮的比较得到了主串和模串前 5 个字符都是相等的,这时我们其实是可以直接跳到第六步的,前面的2、3、4、5 其实都没有意义的,因为模串的第一个字符 ‘a’ 是不可能与2、3、4、5 的字符相等的。
此时便引出 KMP 算法,刚好补助了这一缺点,在回移比较时,回到有意义的位置再次比较
KMP 算法执行流程
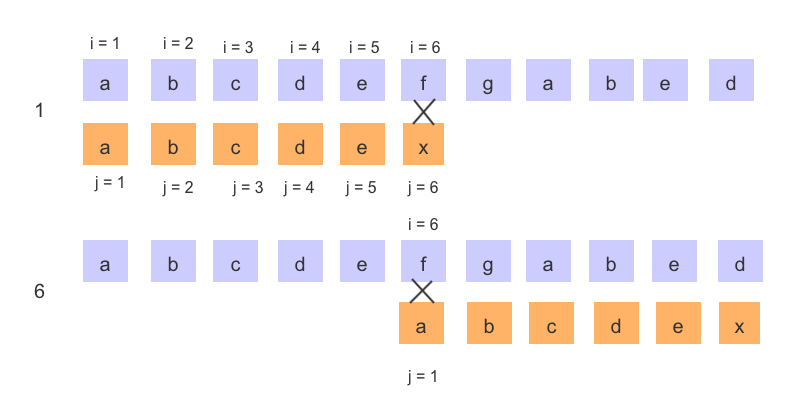
使用 KMP 算法,在经过第一轮比较后,我们知道了,i = 6 并且 j = 6,那么也就是说,前 5 个字符都是相等的,i和 j 才能到 6 这个位置,然后模串中 'a' 字符又是唯一的,那么,'a' 必定也不等于主串中的位置为 2、3、4、5 的字符,所以就可以省略BF 算法中2、3、4、5步,保留 BF 算法中的第六步,因为无法判断 S[6] != T[1],因此这个两个位置字符还需比较一下。
假如有题目二:
假如现在有一个主串 S = "abcababca",模式串 T = "abcabx",找出T 在 S 中完全匹配时的首地址。
这时在模串中字符 'a' 存在不是唯一的这时要怎么处理呢?
BF 算法执行流程
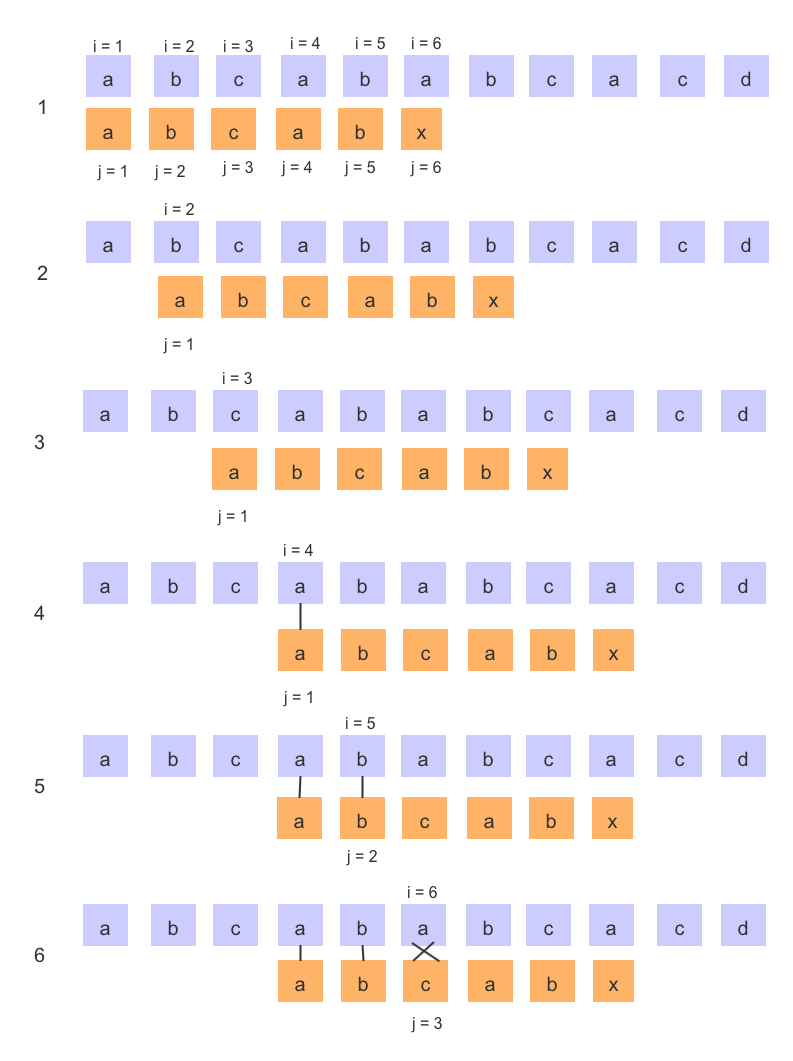
主串与模串跟题目一的字符不同,所以执行流程有所变化,但是缺陷跟题目一中的BF算法一样,于是按照 KMP 算法分析一下
KMP 算法执行流程
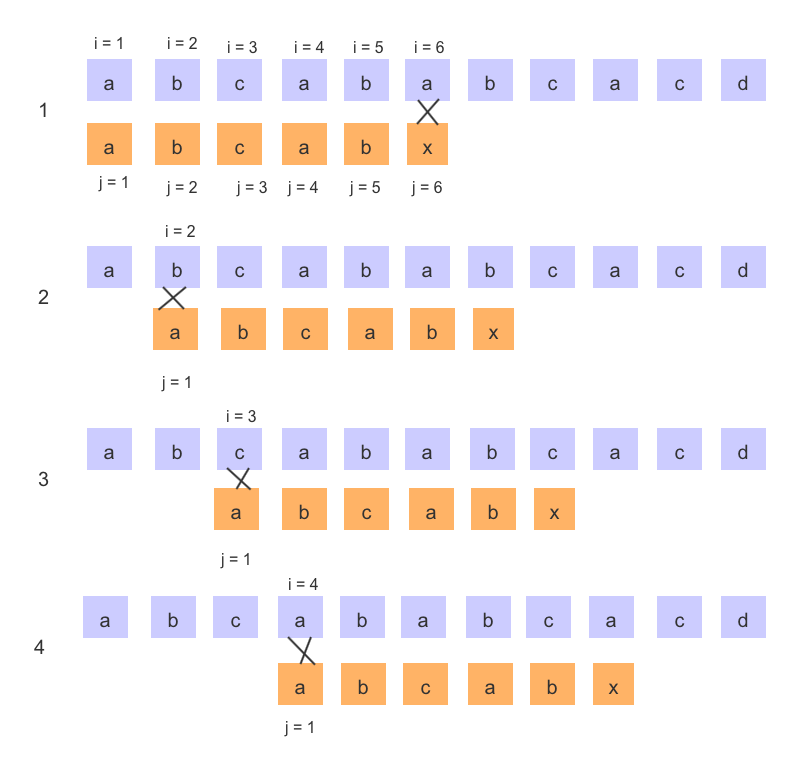
在模串中我们可以看出字符 'a' 在前 3 个字符中是唯一的,并且与主串中的前 3 个字符也是完全相等的,所以根据一题目中 KMP 的经验可知,模串中的字符 'a' 与主串中位置为 2、3 的字符是一定不不等的,所以我们可以说 BF 算法中的 2、3 步是无效的,
然后继续看BF执行步骤
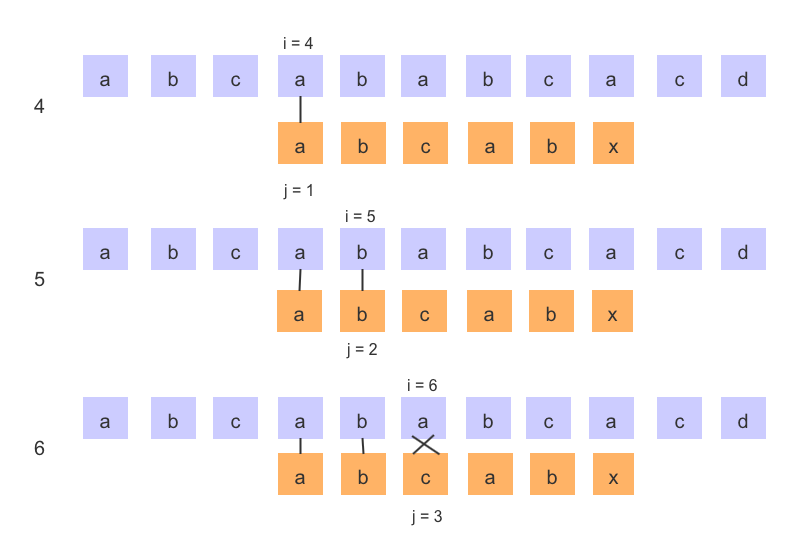
在 BF 算法的第一步就把主串和模串中的 第 1 、第 2 和 第 3 、第 4 的对应的 'a'、'b' 进行比较,得出同地址的字符是相等的,那么也就是说,在第 4 、第 5 步中,又对主串和模串的 'a'、'b' 字符进行比较就是没有意义的,可以对其省略,省略了之后 KMP 算法流程如下
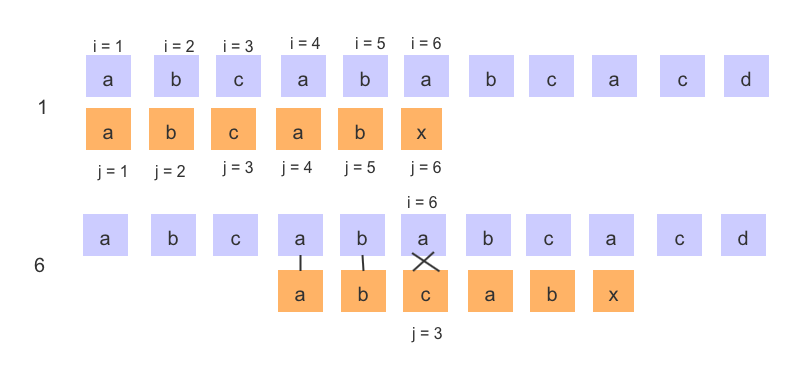
KMP 算法总结
- 当我们在 BF 匹配算法中,当检测到两个字符串不字符不匹配时,i ,j 值就回溯,也是说通过不断回溯主串的 i和模串的 j 值来完成字符匹配的。
- 然后又通过分析又发现 BF 算法中很多回溯是没必要的
- 而 KMP 算法就是为了避免让不必要的回溯发送
对比以上两个题目的分析,我们会发现,模串 T 中首字符 'a' 在整个T串中出现的次数不一样,回溯时,j 的值也会发生变化,也就是说 j 值得变化不知与主串对比有关系,还与模串 T 中字符是否有重复有关。
主串S = "abcdefgabed",模式串 T = "abcabx"

主串 S = "abcababcaed",模式串 T = "abcabx"

所以,回溯时 j 的位置不是固定的,为了更好的推导回溯时,j 的位置,便将模串各个位置 j 的变化定义为一个next 数组, next 的数组长度应与模串数组一样。
KMP 匹配算法中_next 数组值推导
我们把模串 T 各个位置的 j 值对应需回溯的位置变化定义为一个 next 数组,那么 next 的长度就是模串 T 的长度,于是便有一下函数定义
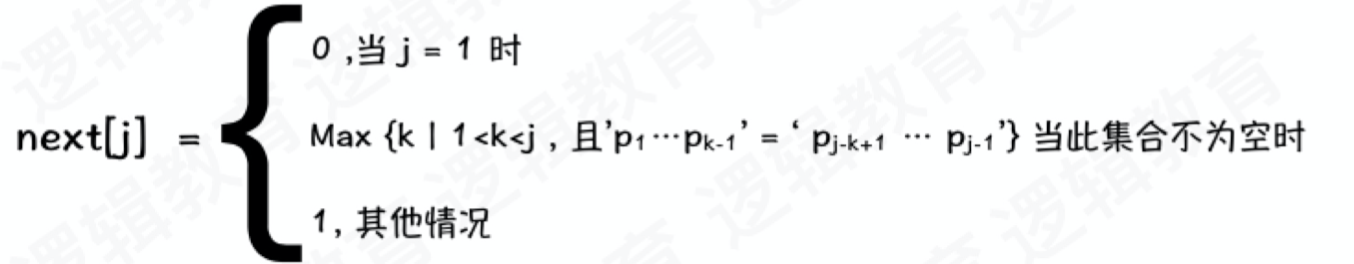
此图的意思是,当j = 1 时,next[j] = 0;
字符串中无重复字符时,next[j] = 1;
当有重复字符或字符串出现时,就看串的前后缀相等字符的个数 n,一个字符相等 n = 1 时,k = n + 1 = 2, 两个字符相等 n = 2 时, k = n + 1 = 3。
情景一:模式串中无重复字符
分析:T = "abcdex"
根据上图进行以下推到
- j = 1 时,1 前面没任何字符----------------------------------故,next[1] = 0;
- j = 2 时,1 - 2 的范围内有字符 'a',并没有重复字符-----------故,next[2] = 1;
- j = 3 时,1 - 3 的范围内有字符 "ab",并没有重复字符----------故,next[3] = 1;
- j = 4 时,1 - 4 的范围内有字符 "abc",并没有重复字符---------故,next[4] = 1;
- j = 5 时,1 - 5 的范围内有字符 "abcd",并没有重复字符--------故,next[5] = 1;
- j = 6 时,1 - 6 的范围内有字符 "abcde",并没有重复字符-------故,next[6] = 1;
可得出,模式串 T = "abcdex", next = {0,1,1,1,1,1};
情景二:模式串中有重复字符
分析:T = "abcabx"
根据上图进行一下推到
- j = 1 时,1 前面没任何字符----------------------------------故,next[1] = 0;
- j = 2 时,1 - 2 的范围内有字符 'a',并没有重复字符-----------故,next[2] = 1;
- j = 3 时,1 - 3 的范围内有字符 "ab",并没有重复字符----------故,next[3] = 1;
- j = 4 时,1 - 4 的范围内有字符 "abc",并没有重复字符---------故,next[4] = 1;
- j = 5 时,1 - 5 的范围内有字符 "abca",前后缀重复字符"a"-----故,next[5] = 2;
- j = 6 时,1 - 6 的范围内有字符 "abcab",前后缀重复字符"ab"---故,next[6] = 3;
可得出,模式串 T = "abcabx", next = {0,1,1,1,2,3};
情景三:模式串类似于 "ababaaaba"
分析:T = "ababaaaba"
- j = 1 时,1 前面没任何字符----------------------------------故,next[1] = 0;
- j = 2 时,1 - 2 的范围内有字符 'a',并没有重复字符-----------故,next[2] = 1;
- j = 3 时,1 - 3 的范围内有字符 "ab",并没有重复字符----------故,next[3] = 1;
- j = 4 时,1 - 4 的范围内有字符 "aba",前后缀重复字符"a"------故,next[4] = 2;
- j = 5 时,1 - 5 的范围内有字符 "abab",前后缀重复字符"ab"----故,next[5] = 3;
- j = 6 时,1 - 6 的范围内有字符 "ababa",前后缀重复字符"aba"--故,next[6] = 4;
- j = 7 时,1 - 7 的范围内有字符 "ababaa",前后缀重复字符"a"---故,next[7] = 2;
- j = 8 时,1 - 8 的范围内有字符 "ababaaa",前后缀重复字符"a"--故,next[8] = 2;
- j = 9 时,1 - 9 的范围内有字符 "ababaaab",前后缀重复字符"ab",故,next[9] = 3;
可得出,模式串 T = "ababaaaba", next = {0,1,1,2,3,4,2,2,3};
注意:
- next 数组是比较连续的前缀字符和后缀字符,例如j = 6 时,字符串 "ababa", 此时 "aba",既是前缀也是后缀。
- 当 i = 7 时,字符串 "ababaa", 此时前后缀相等的字符是 'a',因为 next[j] 对应的值为相同字符个数 n 加 1, 所以 next[7] = 1 + 1 = 2。
情景四:模式串类似于 "aaaaaaaab"
分析:T = "aaaaaaaab"
- j = 1 时,1 前面没任何字符----------------------------------故,next[1] = 0;
- j = 2 时,1 - 2 的范围内有字符 'a',并没有重复字符-----------故,next[2] = 1;
- j = 3 时,1 - 3 的范围内有字符 "aa",前后缀重复字符"a"-------故,next[3] = 2;
- j = 4 时,1 - 4 的范围内有字符 "aaa",前后缀重复字符"aa"-----故,next[4] = 3;
- j = 5 时,1 - 5 的范围内有字符 "aaaa",前后缀重复字符"aaa"---故,next[5] = 4;
- j = 6 时,1 - 6 的范围内有字符 "aaaaa",前后缀重复字符"aaaa"-故,next[6] = 5;
- j = 7 时,1 - 7 的范围内有字符 "aaaaaa",前后缀重复字符"aaaaa",故,next[7] = 6;
- j = 8 时,1 - 8 的范围内有字符 "aaaaaaa",前后缀重复字符"aaaaaa",故,next[8] = 7;
- j = 9 时,1 - 9 的范围内有字符 "aaaaaaaa",前后缀重复字符"aaaaaaa",故,next[9] = 8;
可得出,模式串 T = "aaaaaaaab", next = {0,1,2,3,4,5,6,7,8};
注意:
注意完全相同的情况下,前后缀字符串的标识就可以了
经过以上的分析可以得出:
-
字符串匹配在位置 j = 1 时,回溯位置从下标 0 处开始重新匹配;
-
在其他位置进行回溯时,都要回溯到模串的下标 j 在next数组中对应的值位置进行重新匹配;
-
next 对应的值,就是字符串匹配过程中不相等时的模串的回溯位置。
KMP 模式匹配算法 next 数组回溯位置求解
过程模拟
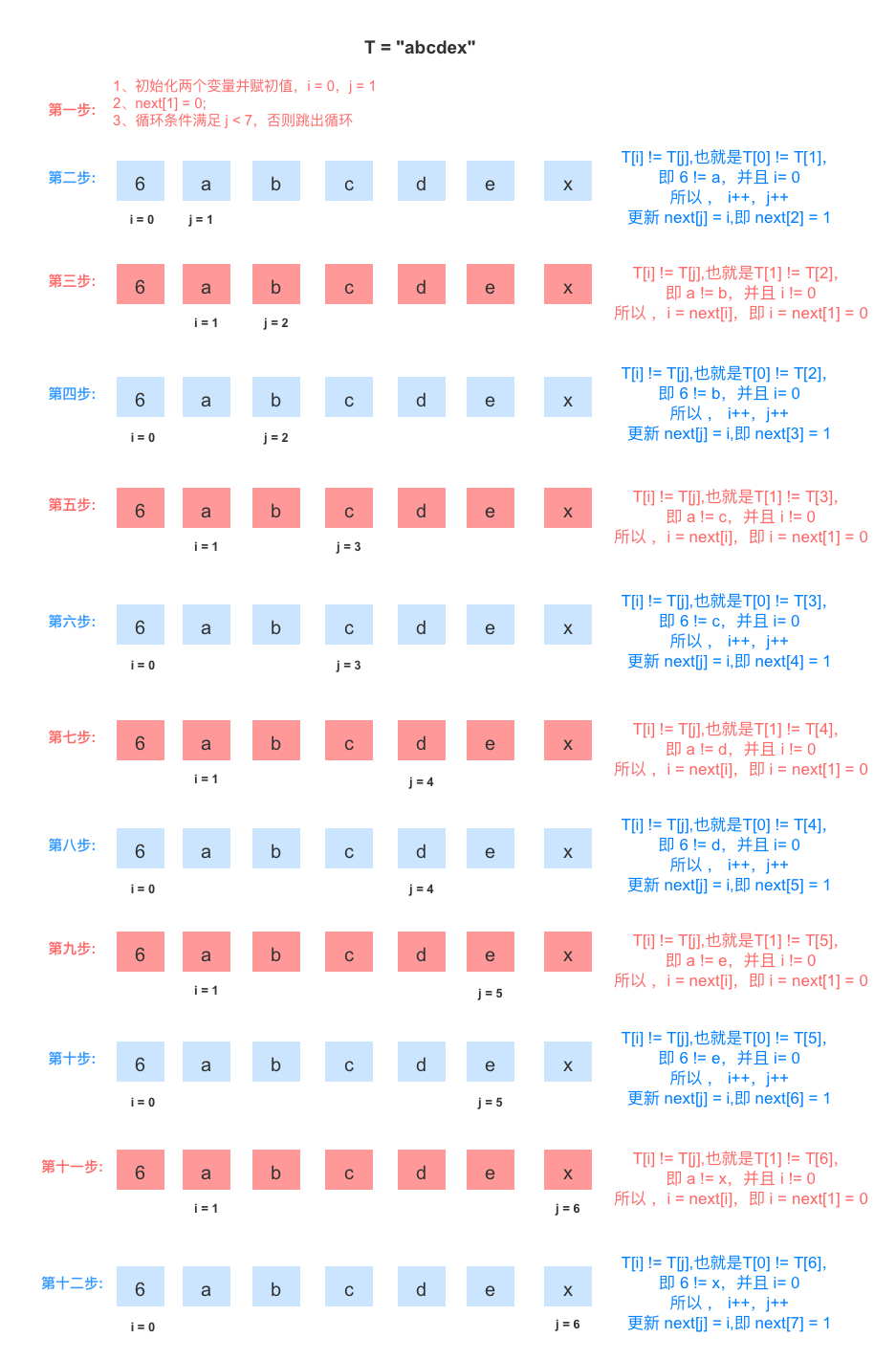
代码实现
//通过计算返回子串 T 的 next 数组
//注意:字符串T[0]中是存储的字符串长度,真正的字符串内容从 T[1] 开始
void get_next(String T, int *next) {
int i = 0, j = 1;
next[j] = 0;
//遍历 T 模式串,此时T[0]为字符串T长度
while (j <= T[0]) {
if (i == 0 || T[i] == T[j]) {
//T[i] 表示后缀的单个字符
//T[j] 表示前缀的单个字符
i++;
j++;
next[j] = i;
// printf("next[%d]=%d\n",j,next[j]);
} else {
//如果字符不相同,则i值回溯
i = next[i];
}
}
}
KMP 模式匹配算法代码实现
#define MAXSIZE 20
typedef char String[MAXSIZE + 1];
void insertString(String T, char *s) {
if (s == NULL) {
printf("字符串为空!");
}
T[0] = strlen(s);
for (int i = 1; i <= T[0]; i++) {
T[i] = s[i-1];
}
}
void printfString(String T) {
if (T[0] <= 0) {
printf("字符串为空!");
}
for (int i = 1; i <= T[0]; i++) {
printf("%c ", T[i]);
}
printf("\n");
}
int get_StrLength(String T) {
return T[0];
}
void pirntfNext(int next[], int length) {
printf("next 数组元素为:");
for (int i = 1; i <= length; i++) {
printf("%d ", next[i]);
}
printf("\n");
}
//通过计算返回子串 T 的 next 数组
//注意:字符串T[0]中是存储的字符串长度,真正的字符串内容从 T[1] 开始
void get_next(String T, int *next) {
int i = 0, j = 1;
next[j] = 0;
//遍历 T 模式串,此时T[0]为字符串T长度
while (j <= T[0]) {
if (i == 0 || T[i] == T[j]) {
//T[i] 表示后缀的单个字符
//T[j] 表示前缀的单个字符
i++;
j++;
next[j] = i;
// printf("next[%d]=%d\n",j,next[j]);
} else {
//如果字符不相同,则i值回溯
i = next[i];
}
}
}
//返回子串T在主串S中第pos个字符之后的位置, 如不存在则返回0;
int index_KMP(String S, String T, int pos) {
//i 是主串当前位置的下标准,j是模式串当前位置的下标准
int i = pos, j = 1;
//定义一个空的next数组;
int next[T[0]];
//对T串进行分析,得到next数组;
get_next(T, next);
//打印next数组
pirntfNext(next, get_StrLength(T));
//注意: T[0] 和 S[0] 存储的是字符串T与字符串S的长度;
//若i小于S长度并且j小于T的长度是循环继续;
while (i <= S[0] && j <= T[0]) {
//如果两字母相等则继续,并且j++,i++
if (S[i] == T[j] || j == 0) {
i++;
j++;
} else {
//如果不匹配时,j回退到合适的位置,i值不变;
j = next[j];
}
}
if (j > T[0]) {
return i - T[0];
}
return -1;
}
int main(int argc, const char * argv[]) {
// insert code here...
printf("字符串匹配算法RK算法!\n");
String T , S;
char *s = "abcababca";
char *t = "abcdex";
//将 s copy 到 s 中
insertString(S, s);
printf("主串为:");
printfString(S);
//将 t copy 到 T 中
insertString(T, t);
printf("模串为:");
printfString(T);
int ret = index_KMP(S, T, 1);
printf("模串在主串中第一次出现的位置为: %d\n",ret);
printf("\n");
char *s1 = "abcababca";
char *t1 = "babc";
//将 s copy 到 s 中
insertString(S, s1);
printf("主串为:");
printfString(S);
//将 t copy 到 T 中
insertString(T, t1);
printf("模串为:");
printfString(T);
ret = index_KMP(S, T, 1);
printf("模串在主串中第一次出现的位置为: %d\n",ret);
return 0;
}
打印结果:

KMP 模式匹配算法优化
存在的缺陷,用图说明
例子 S = "aaaabc" T = "aaaaax"
注意 : 之前数组元素都是从 1 开始存储的,所以读取也是从 1 开始
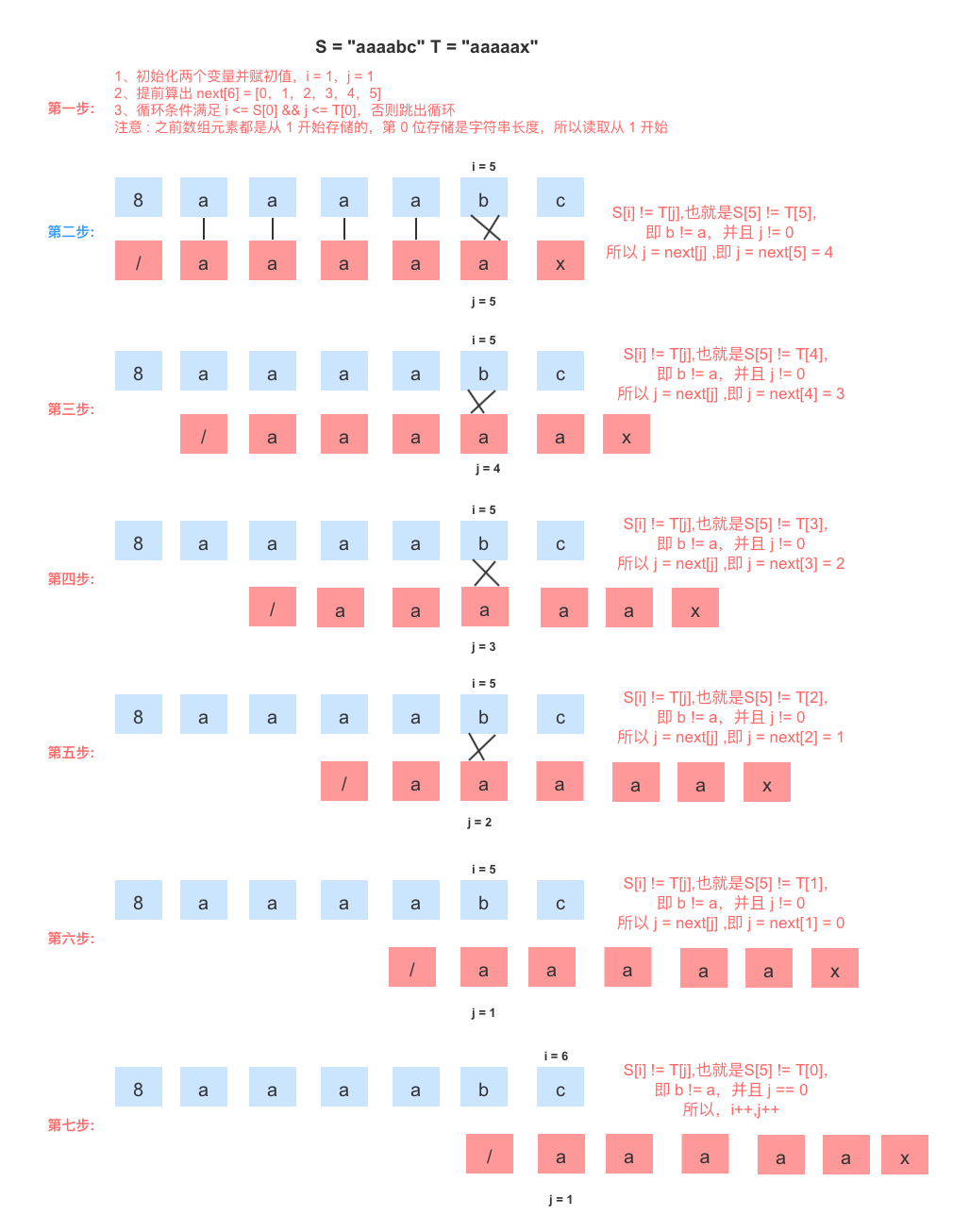
由上图可得:
- 在第一次比较的时候,前五个字符都是一样的,所以, i = 5,j = 5;
- 但是在后面3,4,5,6,7 通过 next 获取回溯位置,反倒还往前移了,达不到正确匹配的效果了
- 模式串 T 字符前 5 个字符都是 'a',还一次往前已,每次都是字符 'b',与字符 'a'比较。
- 到第六步执行完后,此时 j = next[1] = 0,根据KMP 算法再次循环一次,因为 j = 0,所以 i++, j++,,即 i = 6,j = 1;再循序又回到原点,直到 i > S[0],即, i > 6,结束循环,所以 3,4,5,6 这几个步骤就是多余的了。
既然结果就是最后会回到 j = 1, 并且next[1] = 0,所以,优化目标就是要是省略中间的 3,4,5,6 这个几个步骤,直接到达第七步
那么就应该对获取 next 数组的函数进行优化
目前 next = {0,1,2,3,4,5};
如果要节省刚刚 3,4,5,6 的无效不交,需要 next[] = [0,0,0,0,0,0,5];
也就是如果是一样的字符,那么 next 当前位置对应的值就等于,它前面一个相同字符的位置 next 对应的值。
KMP 模式匹配算法 next 数组优化思路图
当 T = "ababaaaba" 时

最后一步 j = 9,T[0] = 9, 因不满足 j < T[0],即,跳出循环。
最后next = {0,,1,,0, 1, 0, 4, 2, 1, 0}
文字有点多,但每一步对照着文字,看是能看懂的。
注意想表达的意思就是在满足 j == 0 || T[i] == T[j] 条件时,j++,i++ 后,在判断一下 T[i] != T[j],如果不等于,next[j] = i,如果等于 next[j] = next[i];
KMP 模式匹配算法 next 数组优化代码实现
//通过计算返回子串 T 的 next 数组
//注意:字符串T[0]中是存储的字符串长度,真正的字符串内容从 T[1] 开始
void get_next(String T, int *next) {
int i = 0, j = 1;
next[j] = 0;
//遍历 T 模式串,此时T[0]为字符串T长度
while (j <= T[0]) {
if (i == 0 || T[i] == T[j]) {
//T[i] 表示后缀的单个字符
//T[j] 表示前缀的单个字符
i++;
j++;
if (T[i] != T[j]) {
next[j] = i;
} else {
next[j] = next[i];
}
} else {
//如果字符不相同,则i值回溯
i = next[i];
}
}
}
打印结果:
