0 前言
今天我们来重点解读Independent Mechanism,这是Modularity涉及的很重要的概念,主要是以下两篇文章:
[1]Parascandolo G, Kilbertus N, Rojas-Carulla M, et al.Learning independent causal mechanisms[J]. arXiv preprint arXiv:1712.00961, 2017.[pdf]
[2] Goyal A, Lamb A, Hoffmann J, et al. Recurrent independent mechanisms[J]. arXiv preprint arXiv:1909.10893, 2019. [pdf]
其中第二篇RIM在Yoshua Bengio的多次演讲中都有出现,足见其重要性。下文的分析没有非常细致,还是建议大家看看paper。
1 什么是Independent Mechanism?
Independent Mechanism(来源于Causality)是指具备极强泛化性独立功能的module。比如图像处理中的颜色变换,在任意的图像上都可以处理。Modularity的核心思想就是要使得神经网络能够自动构建出不同的Independent Mechanism,从而实现好的generalization。对于Independent Mechanism,其Independence还体现在不同的module是相互独立互不影响的。即
Independent mechanisms (IM) assumption: the causal generative process of a system’s variables is composed of autonomous modules that do not inform or influence each other.
其实这里只是术语不一样,实际上和我们前面的blog看到的modularity的核心需求没有变化。对于Modularity,我们面对的主要问题还是如何使神经网络自动学习出不同功能的modules,即这里的independent mechanism?
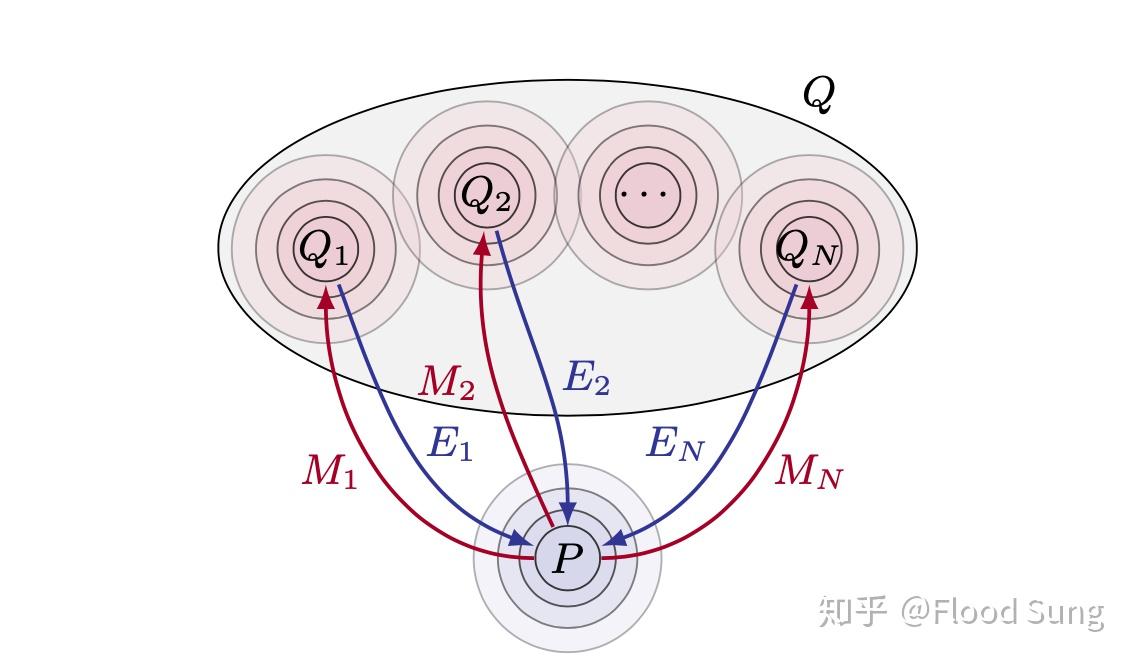
2 问题设定
在之前的文章中,我们并没有看到相关的研究,大部分的研究是基于已知module的构造,或者去统一的学一个layout比如pathnet,但没有对module的功能有过多要求。我们是不是能真正的区分不同的module是个问题。
这篇文章构造了如上图的问题设定,已知一个分布P,我们从P中采样数据然后通过不同的Mechanism M映射到Q中的不同分布,我们希望能够学出不同的inverse mechanism来将Q反向映射回P中。
具体的就是文章中的实验设计,假设我们对MNIST数据集(即P)做预处理,将其通过不同的方法进行变换,比如变形,加噪声,反色,等等不同操作(即M),映射到Q中,我们需要能够学会不同的E将图像反向变回原来的MNIST图像。这里的关键是我们并不知道Q中的数据到底有多少中分布,做了什么变换。
3 基本方法 Competitive Learning
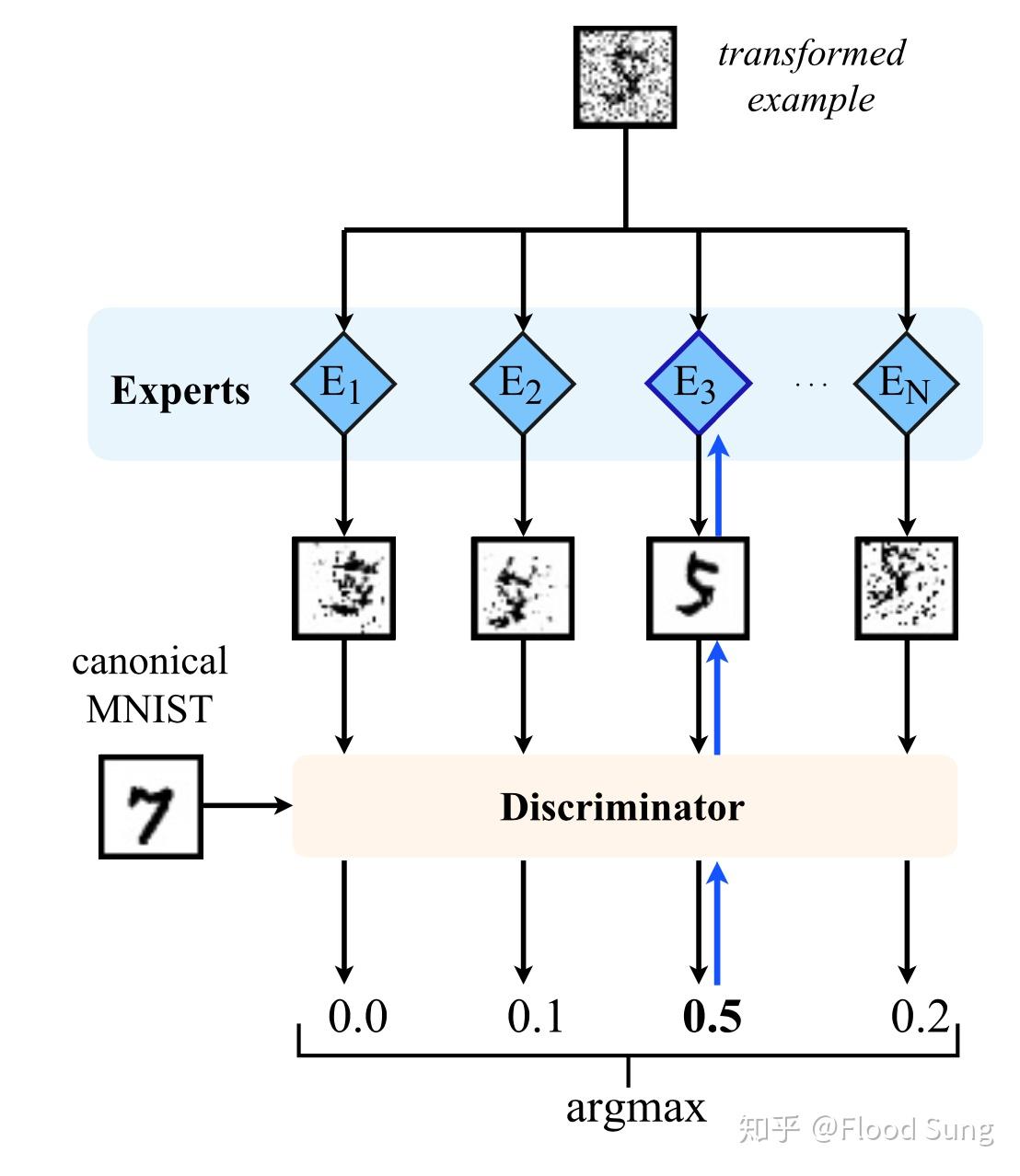
如上图所示,我们有一个变换过后的image,我们想要将其变回原图,但是不知道其用了什么变换。所以这里构造N个expert即independent mechanism,假设不同expert有不同的功能。那么我们就使用每一个expert对图像进行处理,处理完将其输入到一个discriminator中来判断是不是属于原始的图像,选择分值最高的expert进行更新,进一步最大化这个分值,其他experts保持不变(这是关键!)
从直觉上看这个方法很简单,但是实际训练并不容易,因为很有可能训练到最后模型会collapse到某一个或几个expert吧。所以,这里作者加了一个很强的trick称为 approxmate identity initialization ,就是对于每一个expert做预训练,让其先做identity mapping,输入输出一样的图,这样使得不同的expert初始的时候是差不多的,然后训练才有效果。由于这个trick的存在,使得如何更通用的训练出independent mechanism仍然是个问题。但是至少这篇文章带给了我们希望。现在,我们知道modularity很有用,是实现generalization的关键,同时也知道了modularity是有可能通过一定的训练技巧训练出来的。那么,是不是可以构造一个包含independent mechanism的基础网络结构呢?
4 Recurrent Independent Mechanisms
RIM之所以重要是因为这是第一次考虑将modularity直接内嵌到一个基础的网络结构当中,让神经网络的训练结果更具泛化性。RIM是LSTM及Independent Mechanism的拓展,面向序列的输入。
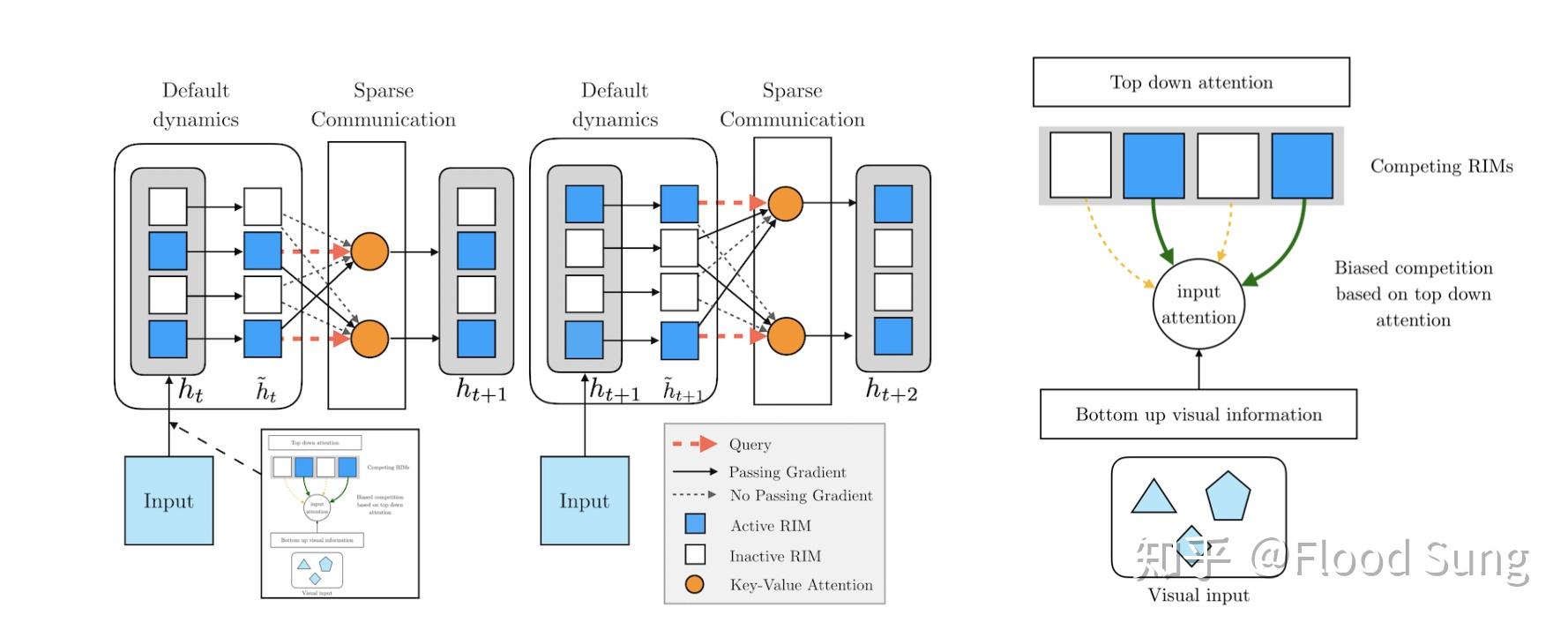
RIMs的整体思路是比较简单的,每一个RIM就是一个独立的神经网络模块,这里采用RNN/LSTM,然后一个cell里面包含了多个RIM。对于每一次的输入input,通过attention的机制让不同的RIM去竞争这个input,选择top k个RIM计算其输出,这个输入的计算同样使用了attention来覆盖所有的RIM(没有选中的RIM不更新,但其里面的信息可能是有用的)。在更新RIM的过程中,被选中的k个RIM才有梯度,其他的RIM的梯度则被block掉了。
这里最需要考虑的是如何使用attention来选择不同的RIM?
5 RIM的Attention机制

首先作者表示这借鉴了心理学的biased competition theory,大致意思是大脑的容量有限,通过competition的方式来选择不同的模块一般是biased,所以总会集中到某些模块上。这里可以认为是Independent Mechanisms的升级,基于这个理论,通过attention的机制可以有效的训练RIM。(这里作者没有一个直接的验证,是否随机初始化就能够有效学到不同的RIM)

在Ablation study中,作者发现每一个RIM的容量要设置的比较小,才能使得RIM充分竞争与合作,否则容易collapse到单个RIM主导的情况。所以RIMs这篇文章也并没有彻底的解决训练问题。
那么在构建attention的过程中,包含了Bottom-Up information flow和Top-down attention两个部分。其中Botton Up information flow是指对图片特征的提取。
Top-down attention实际上是使用每一个RIM的hidden states 和input做交互,算一个选择或不选择这个input的概率。那么作者采用了attention的方式来实现,因此首先在input上concat一个null input,然后让RIM对input和null input做attention,得到的softmax的概率值即为选择input的概率。
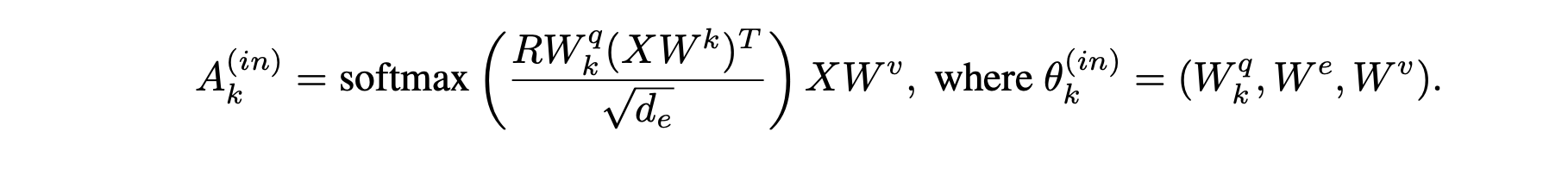
对于每一个RIM,算出一个选择input的概率,然后从这些概率中,选择最高的k个对应RIM,就作为激活的RIM了。这里其实不用attention也可以,直接弄一个f(input,hidden) 输出个选择概率就好了。当然,这里作者还使用了multi-head attention来处理,等价于计算了多个概率取平均。
抛开attention的方法计算,RIM如何根据Input来选择是个问题。由于作者仅考虑sequence的任务,所以使用hidden state来选择input也算合理。
除此之外,作者还构造了RIM之间的communication,使得被选择的RIM可以从没有被选择到RIM中获取信息,这里同样使用了Attention的方式,同时额外使用了residual connection来防止梯度消失。
6 RIM的启发与思考
RIMs设计的核心思想就一句话:
Multiple RIMs can be active, interact and share information.
通过Competitive Learning的竞争机制,使得RIM能够相互独立,同时通过communication,然后不同RIM又能合作。这样RIMs从整体上既有合作又有竞争。
但是,RIMs真的解决了独立性问题吗?从实验上看RIMs确实Generalization能力更强,但是却并没有显著的实验表明每一个RIM的功能不一样。
总的来说,RIMs已经向前迈出了一步,一种具备极强generalization 能力的通用神经网络结构或许就要出现。