算法基础06 - 字典树、并查集、高级搜索、红黑树、AVL 树

Varian米大王
356 阅读5分钟

字典树（Trie 树）

基本结构

字典树是一颗沿着单词中字母排列顺序扩展的多叉树，典型应用是用于统计和排序大量的字符串（但不仅限于字符串），优点是最大限度减少无谓的字符串比较，查询效率比哈希表高。

单词leet在Trie树中的表示

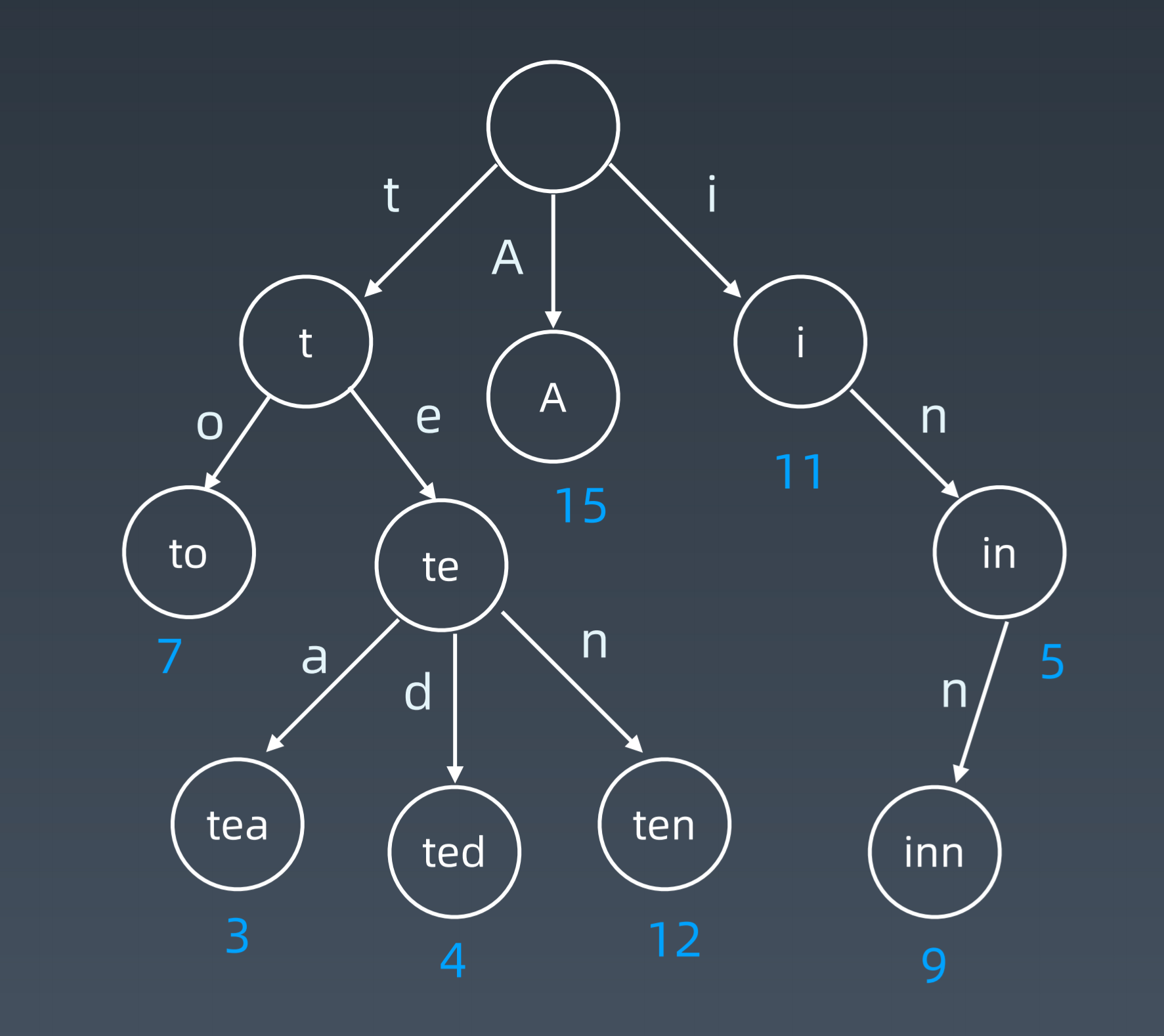
单词leet在Trie树中的表示

核心思想

Trie 树的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

主要用途

  • 搜索引擎输入栏的自动补全
  • 拼写检查
  • IP 路由最长前缀匹配
  • 打字预测

经典问题

212.单词搜索 II

思路：

  • Trie树+DFS+剪枝，时间复杂度O(m * n * 4 * 3^(L-1))，L-单词最大长度，m * n - 网格单元数，空间复杂度O(N) N-字典中字母总数

Python解法

class Solution:
    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
        # 构建 Trie
        trie = {}
        for word in words:
            node = trie
            for char in word:
                node = node.setdefault(char, {})
            node['#'] = True
        # DFS
        def _dfs(i, j, node, pre, visited):
            if '#' in node:
                res.add(pre)
            for (di, dj) in ((-1,0), (1,0), (0, -1), (0, 1)):
                x, y = i+di, j+dj
                if 0 <= x < m and 0 <= y < n and board[x][y] in node and (x,y) not in visited:
                    _dfs(x, y, node[board[x][y]], pre+board[x][y], visited | {(x,y)})
        # 主逻辑
        res, m, n = set(), len(board), len(board[0])
        for i in range(m):
            for j in range(n):
                if board[i][j] in trie:
                    _dfs(i, j, trie[board[i][j]], board[i][j], {(i,j)})
        return list(res)

并查集

并查集，英文名 disjoint set，是用于处理不交集的合并以及查询问题的树形结构。

基本操作

  • MakeSet(s)：创建一个新的并查集，其中包含s个单元素集合

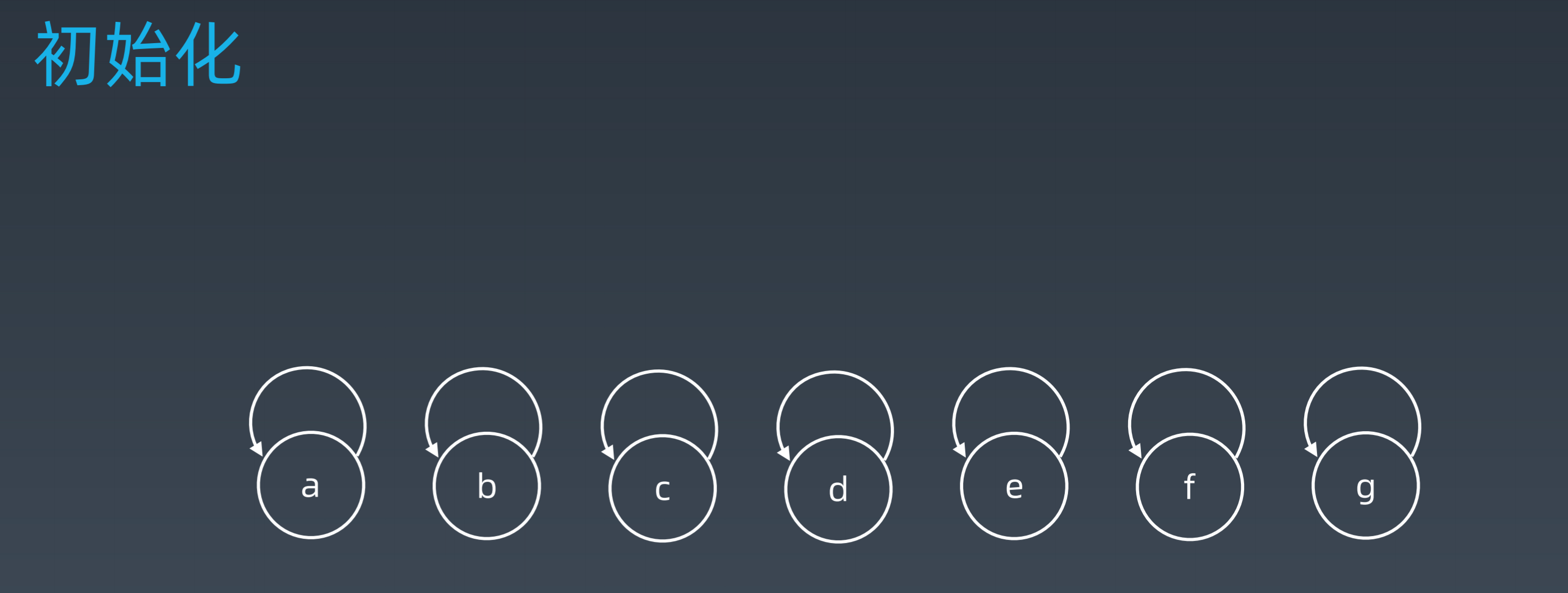
  • Union(x, y)： 将两个子集合并为一个

  • Find(x)： 找到元素所在集合的代表，进而确定元素属于哪一个子集

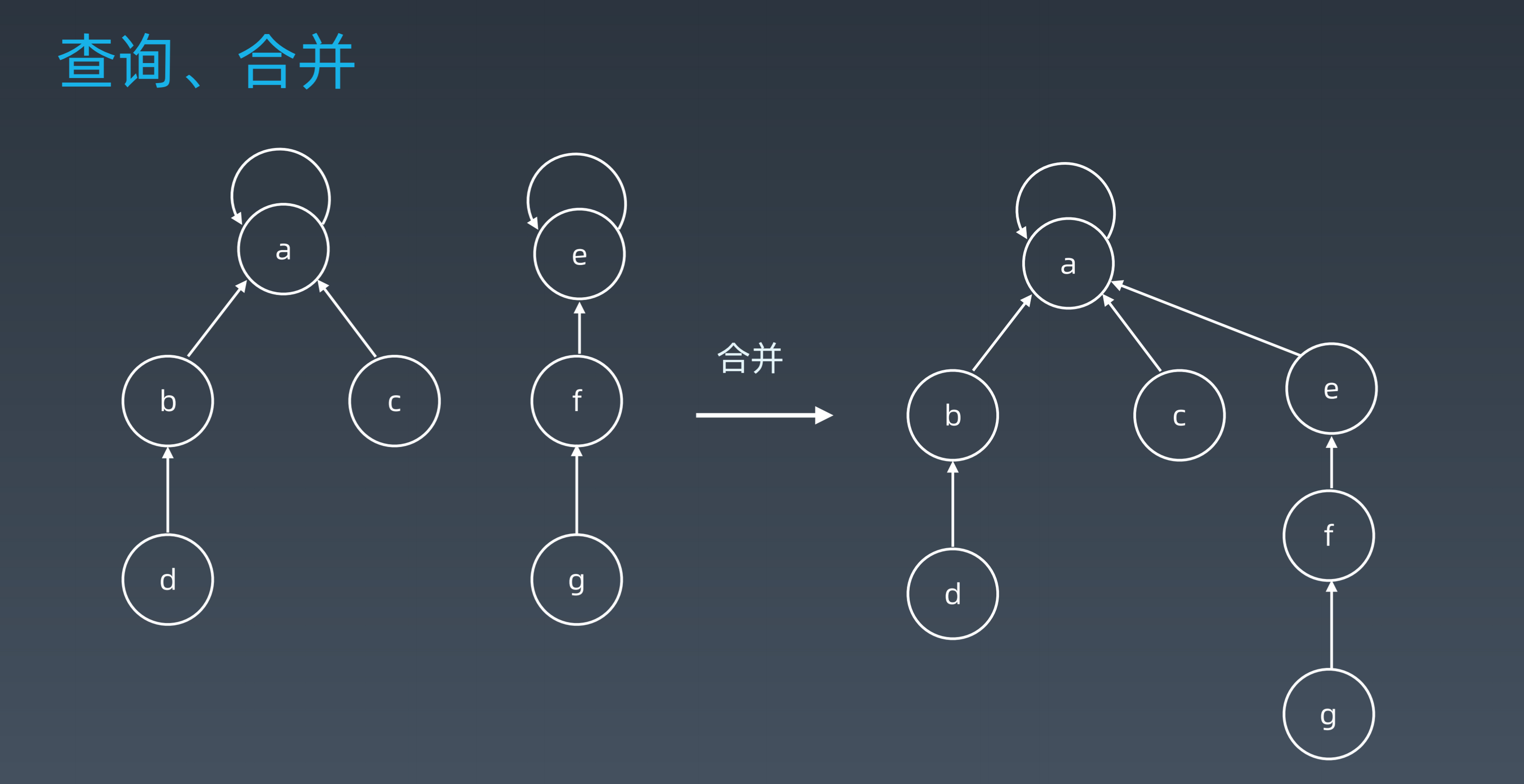
使用路径压缩可以使未来的查询时间复杂度降为 O(1)

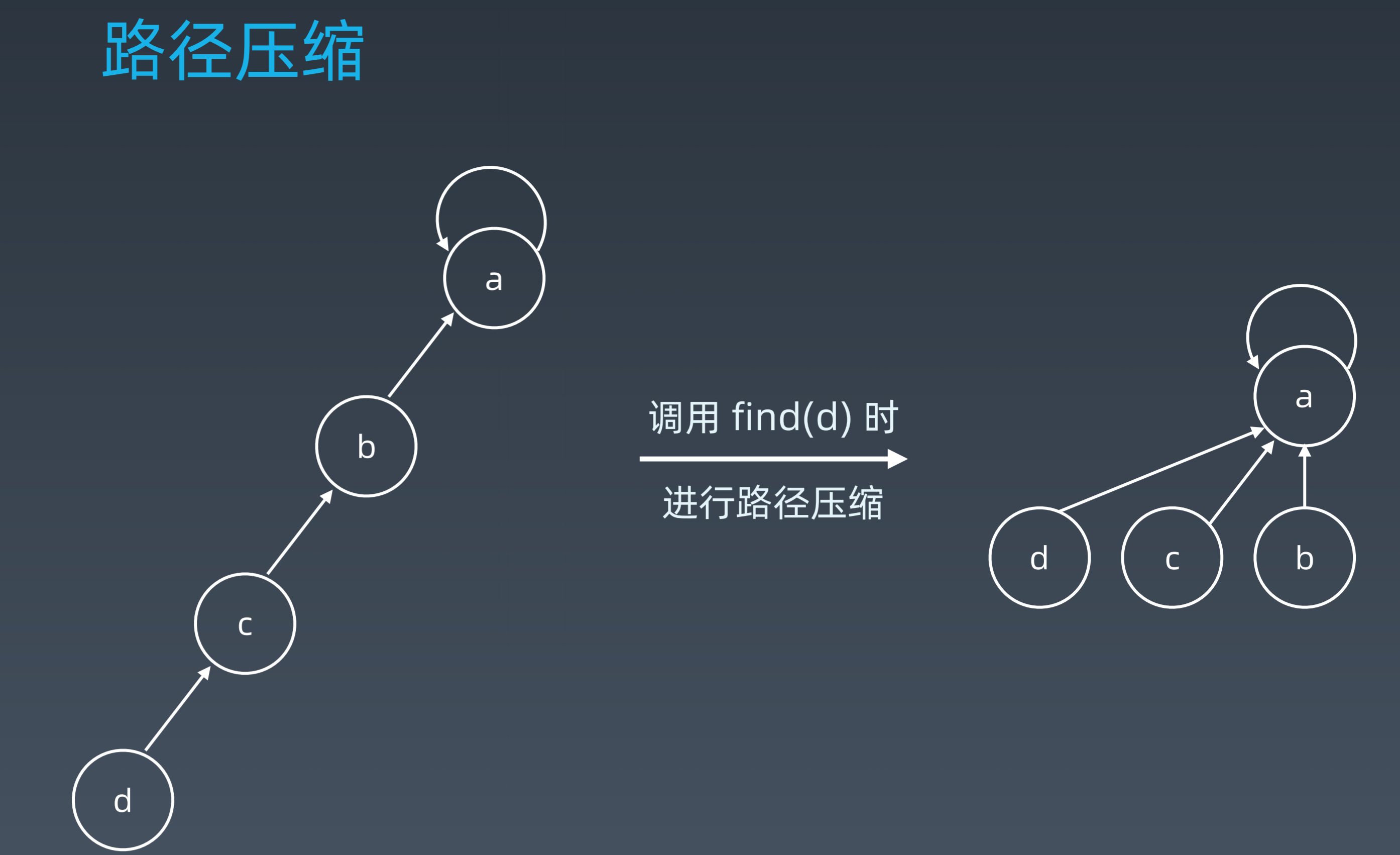
代码模板

def init(p): 
	# for i = 0 .. n: p[i] = i; 
	p = [i for i in range(n)] 
 
def union(self, p, i, j): 
	p1 = self.parent(p, i) 
	p2 = self.parent(p, j) 
	p[p1] = p2 
 
def parent(self, p, i): 
	root = i 
	while p[root] != root: 
		root = p[root] 
	while p[i] != i: # 路径压缩
		x = i; i = p[i]; p[x] = root 
	return root

高级搜索

想知道高级搜索之前，我们先来看看什么是初级搜索

初级搜索

  1. 暴力搜索
  2. 优化方向：剪枝、缓存
  3. 搜索方向：DFS、BFS

高级搜索是对初级搜索的进一步改良，比如双向搜索、启发式搜索等。

双向搜索

核心思想是开始和结束位置同时开始搜索，如果能在中间相遇，说明可以搜索到，如果无法相遇，说明搜索不到。双端BFS是最典型的双向搜索技巧。

双端BFS搜索时间复杂度

O(b^d/2 + b^d/2)，b - BFS每层的宽度，d - 图的深度

普通BFS的时间复杂度为O(b ^ d)，可以通过数学证明双端BFS时间复杂度会比普通BFS快很多。

双端BFS代码模板

public <T> two-endedBFS(begin, end, Container) {
    if (Container.length == 0 || !Container.contains(end)) return NEGATIVE;
    Set<T> beginSet = new HashSet<>(), endSet = new HashSet<>();
    beginSet.add(begin);
    endSet.add(end);
    
    Set<T> visited = new HashSet<>();
    int level = 0;
    
    while(!beginSet.isEmpty() && !endSet.isEmpty()) {
        if (beginSet.size() > endSet.size()){
            Set<T> set = beginSet;
            beginSet = endSet;
            endSet = set;
        }
        Set<T> temp = new HashSet<>();
        for (T item: beginSet){
            T next = generate_nextLevel_nodes();
            if (endSet.contains(next)) return POSITIVE;
            if (Container.contains(next) && !visited.contains(next)){
                temp.add(next);
                visited.add(next);
            }
            // reverse node states
        }
        beginSet = temp;
        level++;
    }
    return NEGATIVE;
}

启发式搜索

启发式搜索，也叫A*算法，它的本质就是优先搜索。根据问题不同，定义不同的优先级比较器，按照优先级从大到小搜索。由于实现一般比较复杂，这里不作代码方面的展开。

红黑树 & AVL树

二叉搜索树的查询时间复杂度只跟树的深度有关，所以为了高效查询，需要保证每个节点子树的深度差不能过大，如此便诞生了平衡二叉树，其中最有名的是红黑树和AVL树。

AVL树特点

  • Balance Factor（平衡因子）：左右子树的高度差，通常限制在 {-1, 0, 1} 范围内

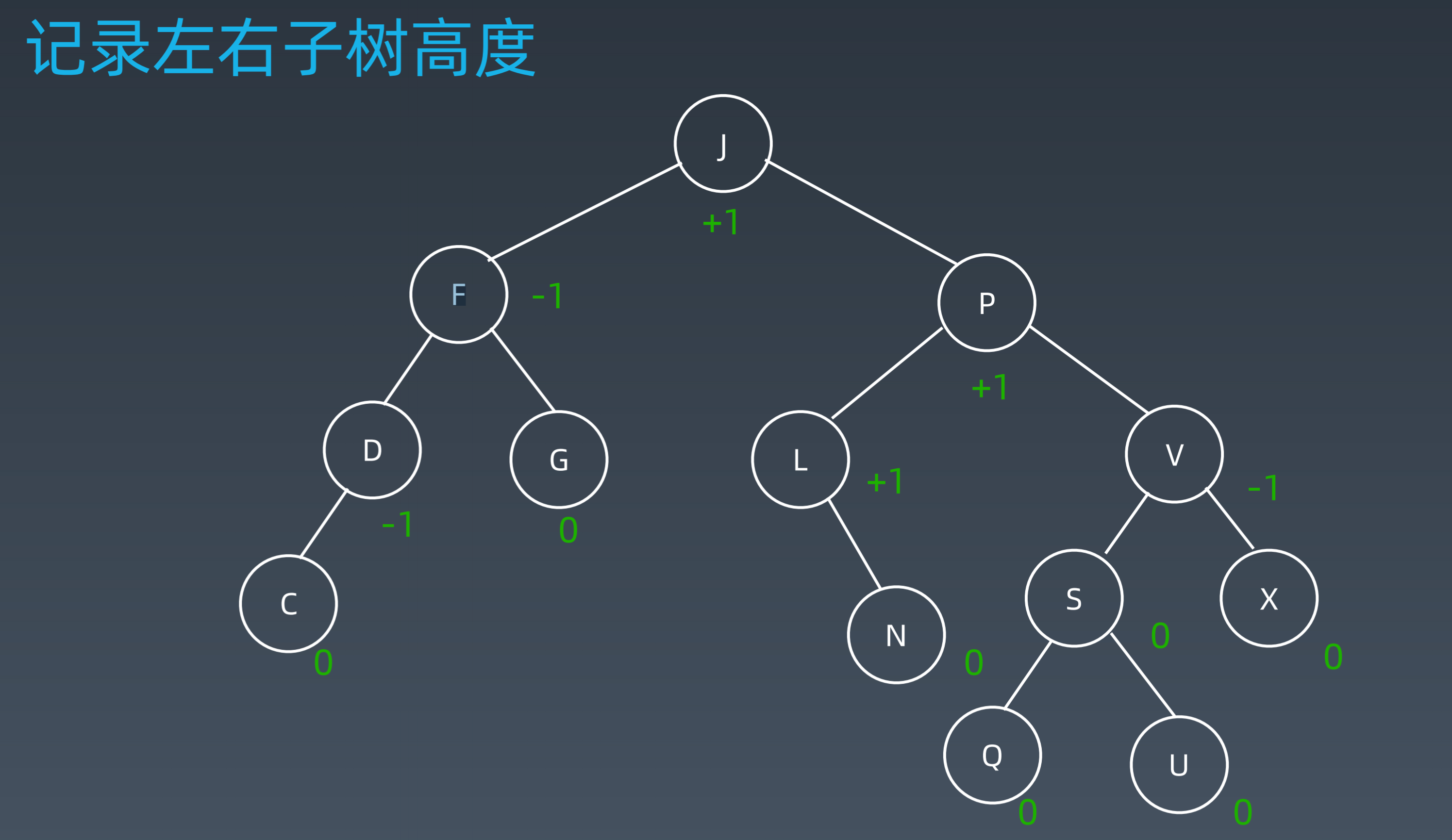
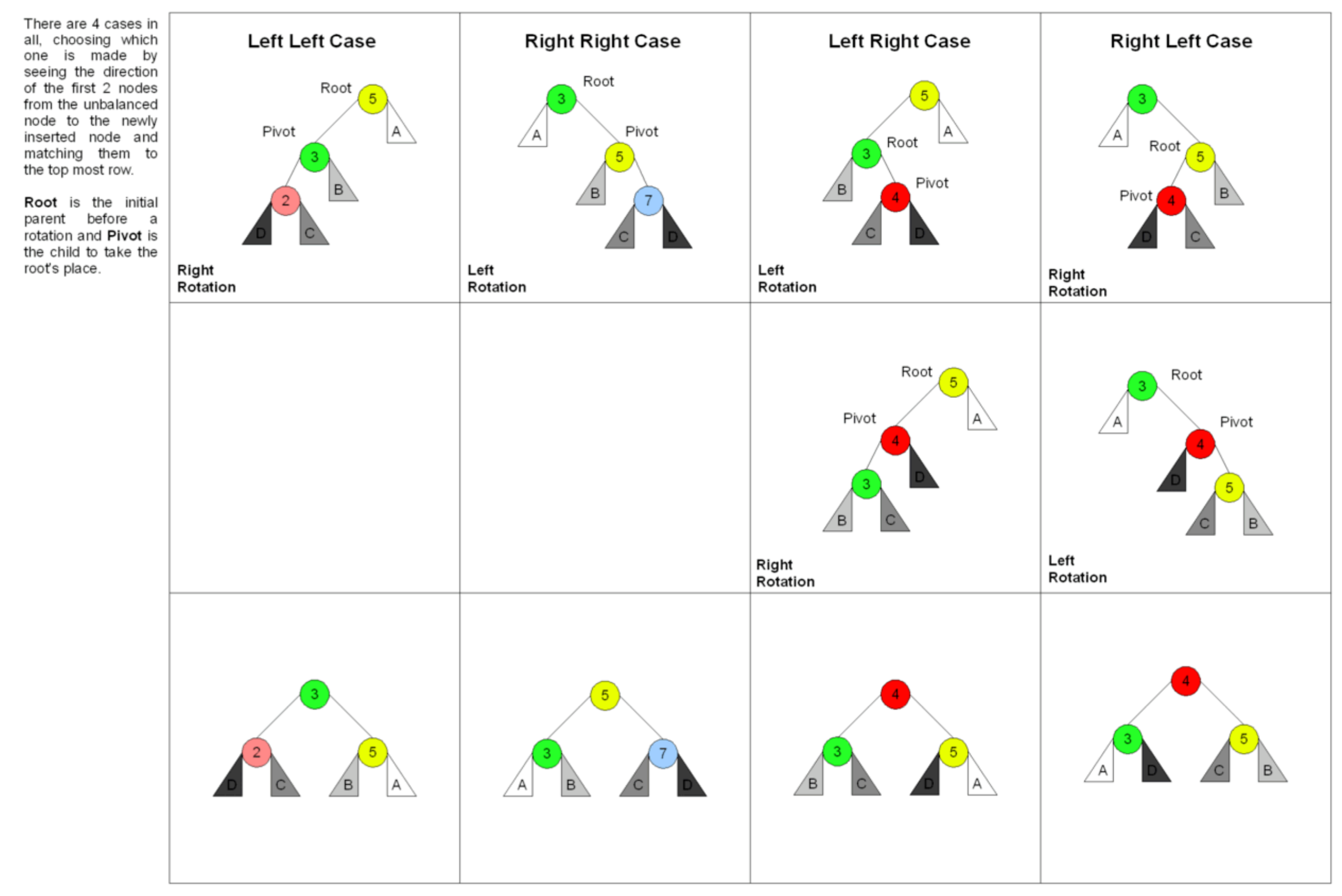
  • 通过旋转操作来进行平衡：左旋、右旋、左右旋、右左旋

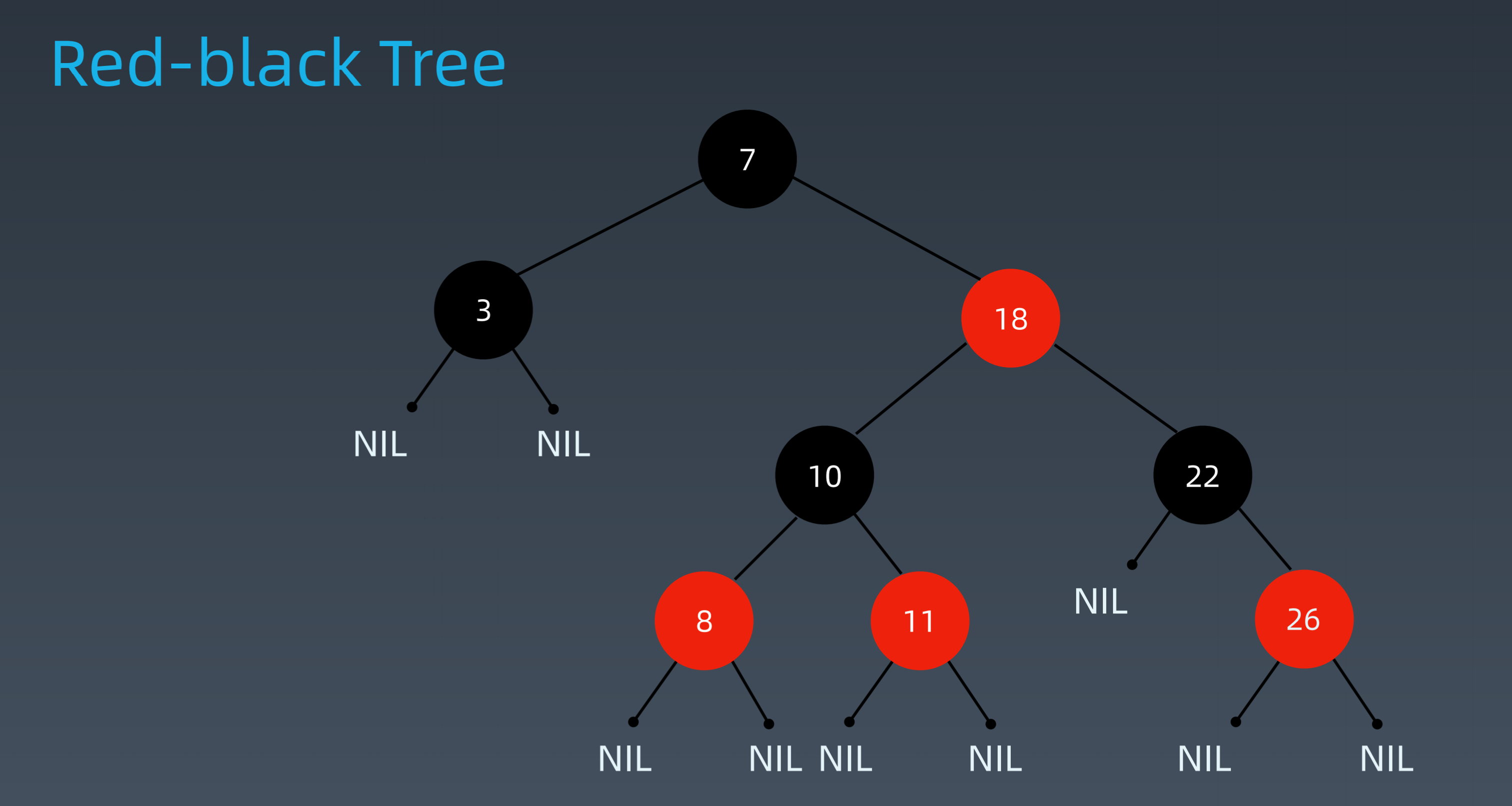
红黑树特点

红黑树是一种近似平衡的二叉搜索树，它可以确保任何一个节点的左右子树的高度差小于两倍。

  • 每个节点要么红，要么黑

  • 根节点是黑色

  • 每个子叶节点（NIL节点）是黑色的

  • 不能有相邻接的两个红色节点

  • 从任一节点到其每个子叶的所有路径都包含数量相同的黑色节点

  • 最关键的性质是：从根到叶子的最长可能路径不多于最短的可能路径的两倍长

AVL & 红黑树比较

  • AVL查询更快，因为更加严格平衡

  • 红黑树增加删除更快，因为相比AVL，红黑树需要的旋转操作更少

  • AVL要存储平衡因子或子树高度，所以会消耗更多空间，而红黑树每个节点只需要1位信息（红 or 黑）

  • 所以读操作非常多写操作不多时，AVL更好；写操作较多或读写参半时红黑树更好；

  • 比如主流语言的库函数如map等是用红黑树实现的，而数据库用AVL实现较多

avatar
文章
阅读
粉丝