算法-再战KMP

DragonetZ
398 阅读7分钟

前言

之前对KMP稍微学习过，是通过一道算法题算法题-查找子串第一次出现和KMP算法学习延伸到的，说实话学的不是那么透彻，这次我们仔细再品品这个算法。

原理探索

KMP优势

主串S中找到模式串T第一次出现的位置，我们使用暴力（BF）法过程中，会有很多没必要的比较，例如：（本文中字符串索引都是以1开始）

图1
i为主串索引，j为模式串索引。图片中很直观的可以看到前两个字符是相等的。继续向后比较，当i=3，j=3时：
图2
发现字符不匹配，i回退到2，j回退到1：
图3
其实通过前面的比较我们知道，主串S中S[1]和S[2]是不相等的，模式串中T[1]和T[2]也是不相等的；而且S[1]==T[1],S[2]==T[2]。所以这一步的比较是完全没有必要的：
我们很容易就能知道，在两个字符串比较的过程中，这种重复的操作会有很多，尤其是使用暴力法。那我们如何去过滤掉这些无意义的比较呢？这就是KMP存在的意义了。

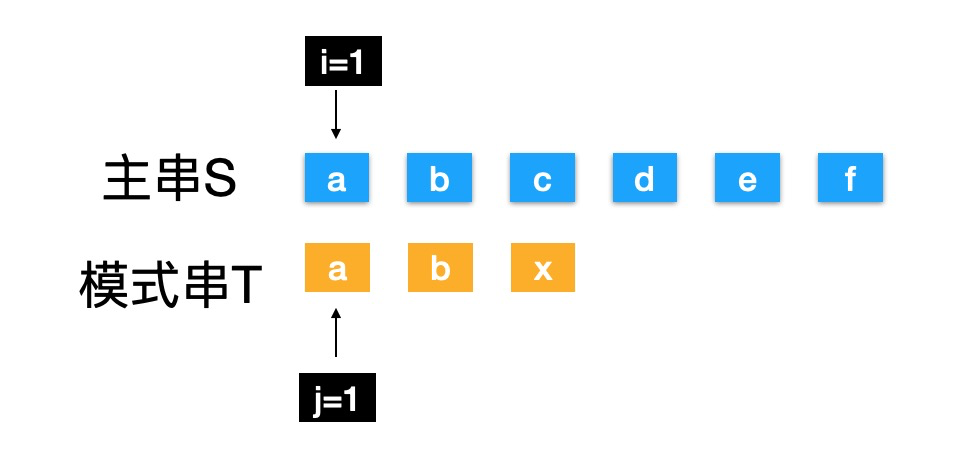
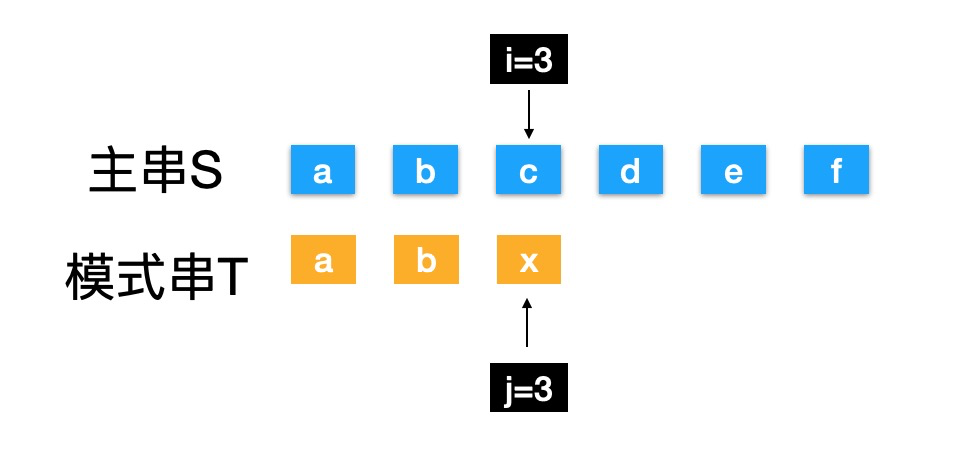
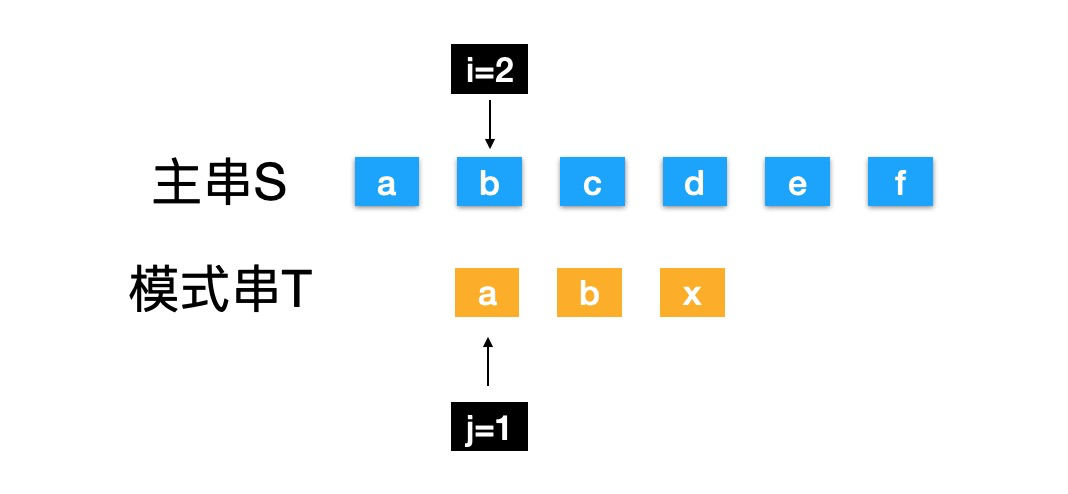
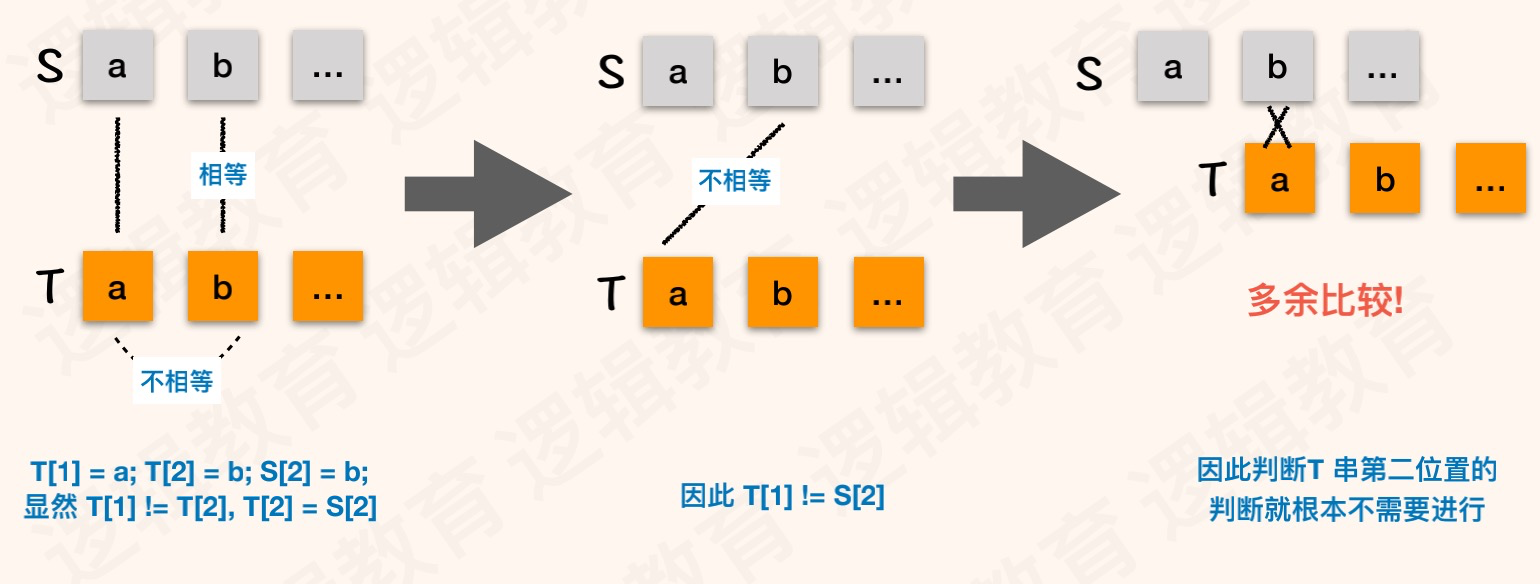
KMP逻辑

回溯数组

KMP主要的核心逻辑，通过模式串中字符的位置生成一个回溯标记数组。

由于上面的例子中模式串太简单了，无法体现出来KMP的精髓，我们换一个例子：

S = "abcabdabcabe", T = "abcabe"

我们先展示模式串T的回溯数组，一会我们再探讨如何求出回溯数组：
注意：回溯数组是通过模式串T生成的，所以和主串S没有关系

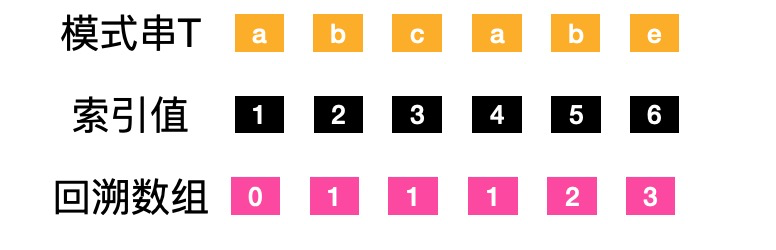
接下来我们用几张图简单模拟一下匹配过程：

  1. 当i=1~5的时候，字符都是匹配的
  2. 当i==6时，S的"d" 不等于 T的"e"
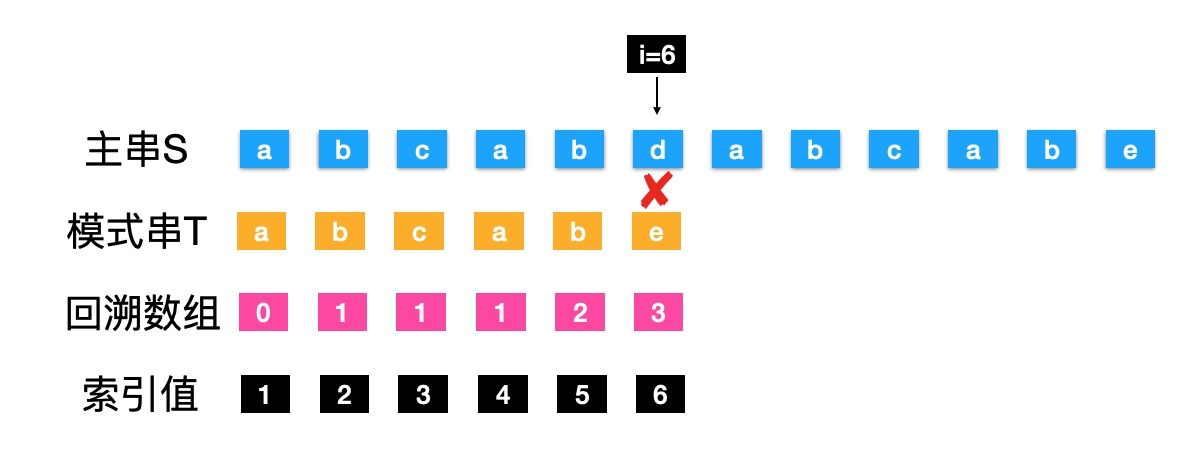
  3. "e"的回溯数组值为3，也就是T回溯到索引值3的位置
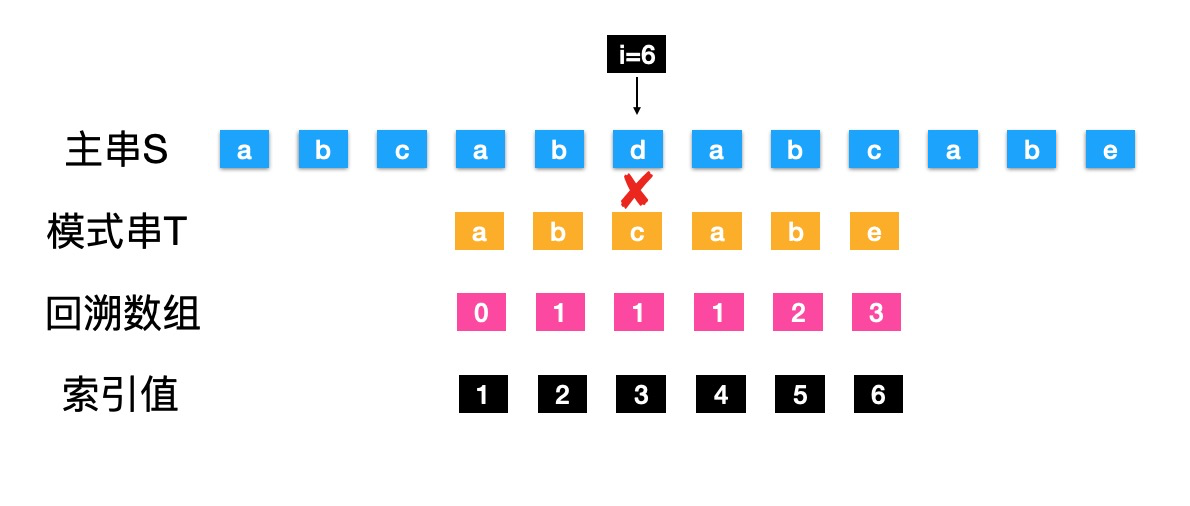
  4. S的"d" 不等于 T的"c"，"c"的回溯数组值为1，T回溯到索引值1的位置
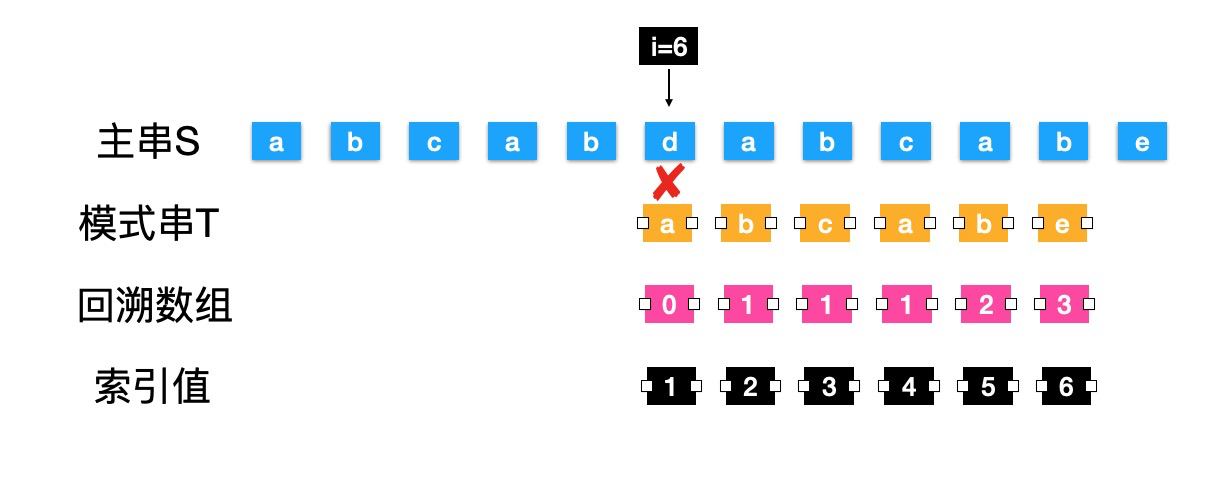
  5. 当前的字符还是不匹配，但是模式串已经到头部了，此时继续向主串S后面的字符做对比，i++
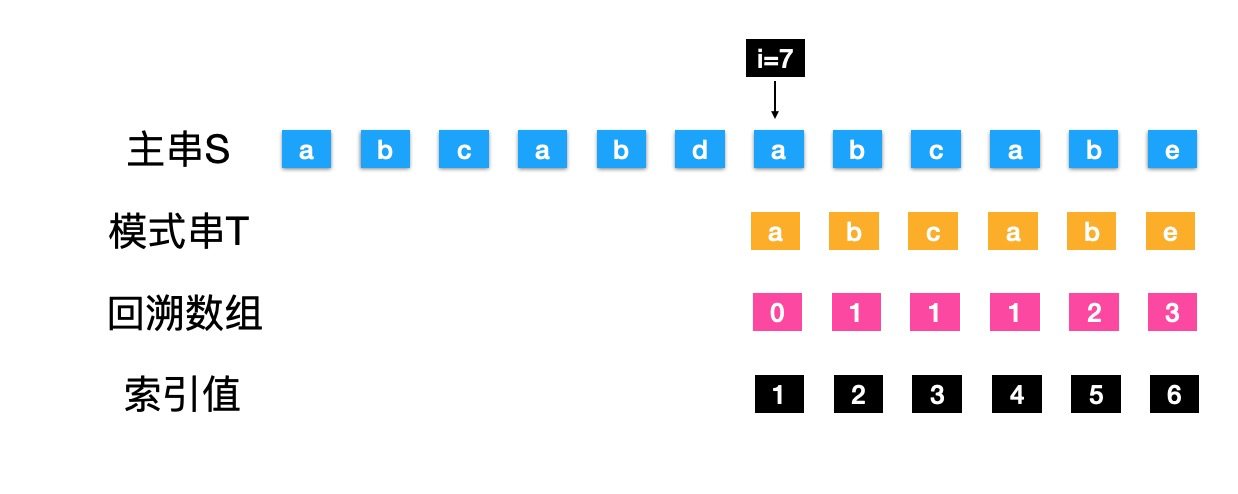
  6. 匹配成功

很明显，通过上面的示例，很容易的看出来匹配过程中，少了很多没必要的匹配步骤。是不是感觉很奇妙。哈哈!大家可以修改主串，自己多试几次。接下来我们要开始最不好理解的环节了，如何创建回溯索引数组了？？？

创建回溯数组

以下我们用next标示回溯数组，数组下标我们用j标示，next数组的长度就是模式串T的长度。我们来看看下面的这张图：

这张图是回溯数组的函数定义，主要分三个部分。我们通过示例来解释一下。T = "abcabe"，如图

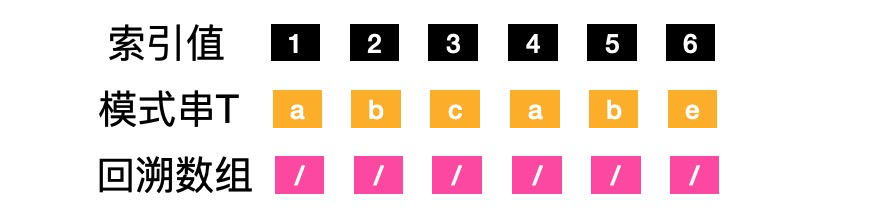
  1. 第一部分，j=1时，就是第一个元素，这个值是0，这个是固定的。其实很好理解，如果第一个字符就不匹配，那就没必要回溯了。

  2. 最后一部分，就是不满足其他两个部分的，直接赋值为1。

  3. 中间，函数定义的中最复杂的部分：

    大概意思：取最大值{存在一个k值，这个k取值范围是1到数组长度（也是T的长度），“前缀”字符串 = “后缀”字符串}

    • 前缀字符串：如果字符串长度为l，那么从字符串的首字符开始，长度从0到l-1都是该字符串的前缀字符串，例如："abcabe"的前缀字符串有{"a","ab","abc","abca","abcab"}
    • 后缀字符串：与前缀相反，从字符串的最后一个字符开始向前数，长度从l到1都是该字符串的后缀字符串，例如："abcabe"的后缀字符串有{"e","be","abe","cabe","bcabe"}

我们根据公式来创建回溯数组next：

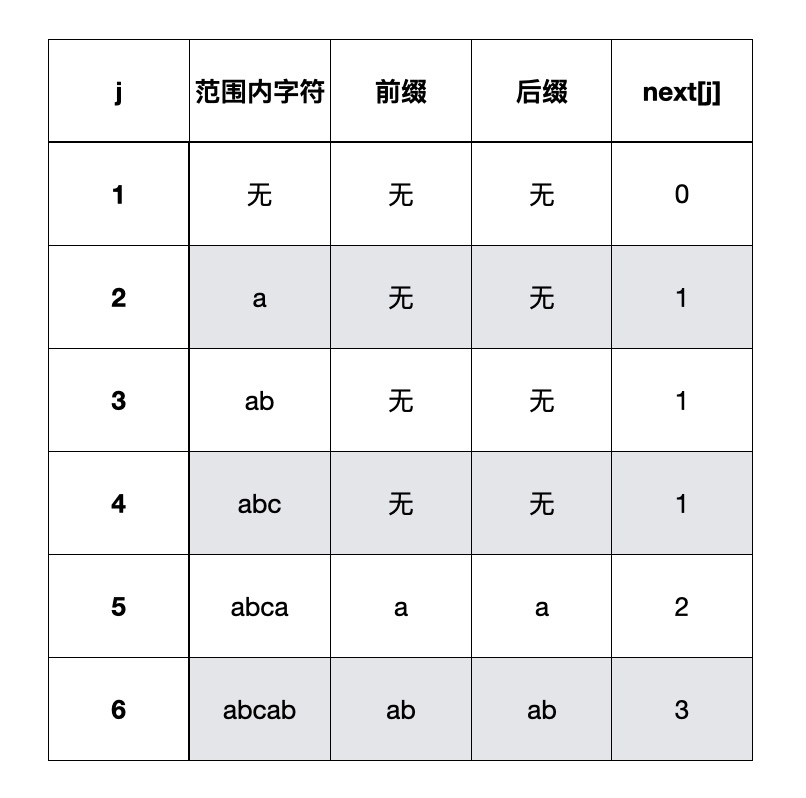
  • j=1，根据公式的第一部分说明，next[j]=next[1]=0
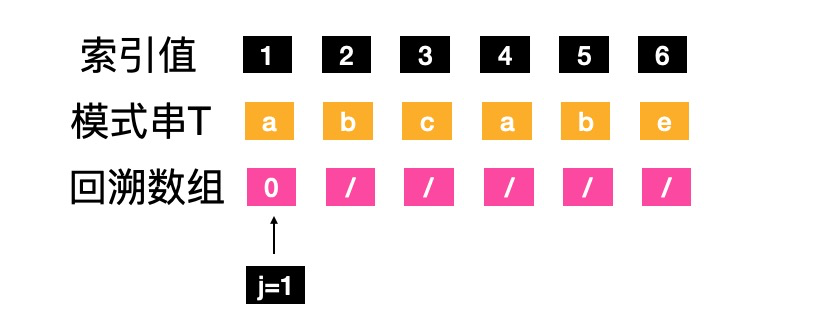
  • j=2，1到j-1，范围内的字符“a”，没有前缀和后缀，也就是属于函数定义的最后一部分的“其他情况”，next[j]=next[2]=1
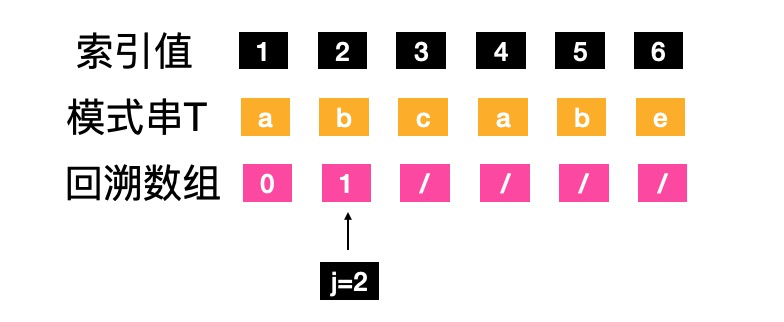
  • j=3，1到j-1，取字符“ab”，没有前缀后缀，属于“其他情况”，next[j]=next[3]=1
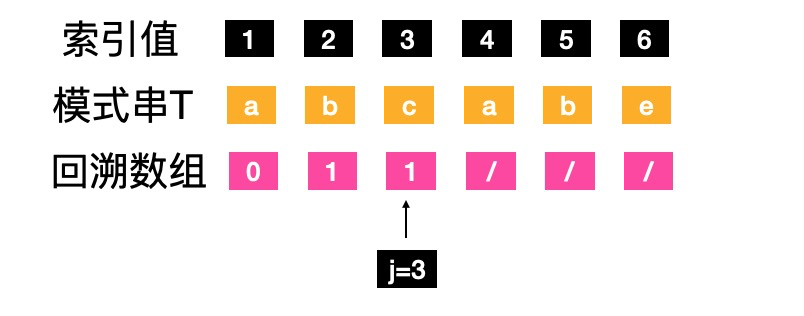
  • j=4，1到j-1，字符“abc”，没有前缀后缀，属于“其他情况”，next[j]=next[4]=1
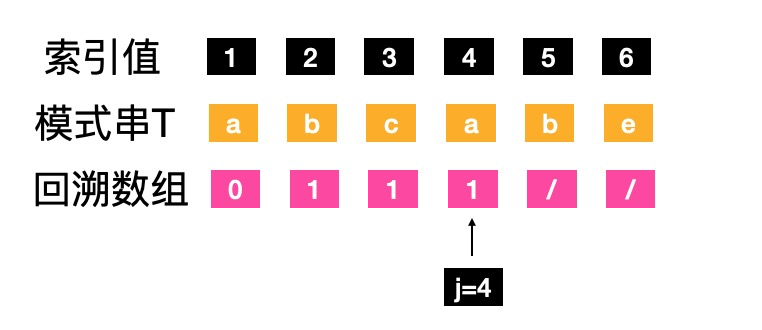
  • j=5，1到j-1，字符“abca”，前缀"a"和后缀"a"相等 (由于 ’p1…pk-1’ = ‘ pj-k+1 … pj-1’,得到p1 = p4)，推到出k=2，next[j]=next[5]=2
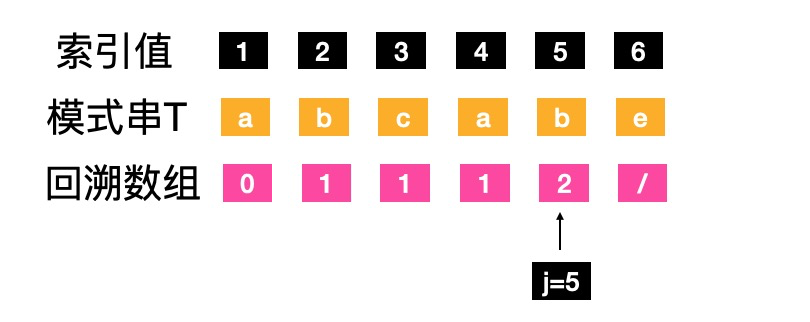
  • j=6，1到j-1，字符“abcab”，前缀"ab"和后缀"ab"相等 (由于 ’p1…pk-1’ = ‘ pj-k+1 … pj-1’,得到p1 = p4)，推到出k=3，next[j]=next[6]=3

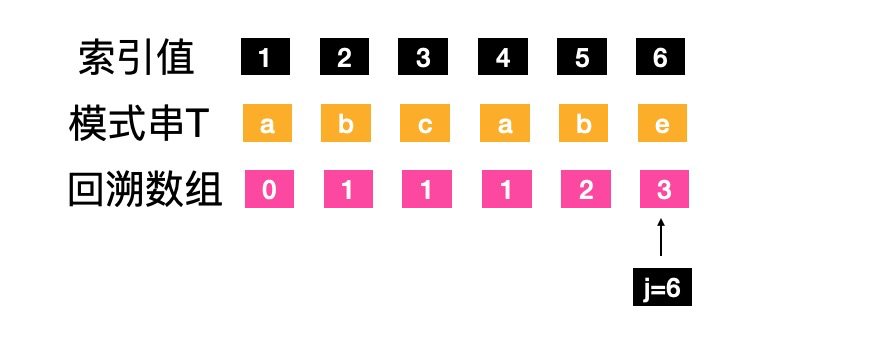
经验: 如果前后缀一个字符相等,K值是2; 两个字符相等是3; n个相等k值就是n+1;

用表格展示公式推到过程

练习一下其他示例

这个回溯数组是KMP很核心的部分，也是很绕的部分，希望大家 按照上面的流程多用几个示例练习一下。以下是一些特殊情况，可以试试

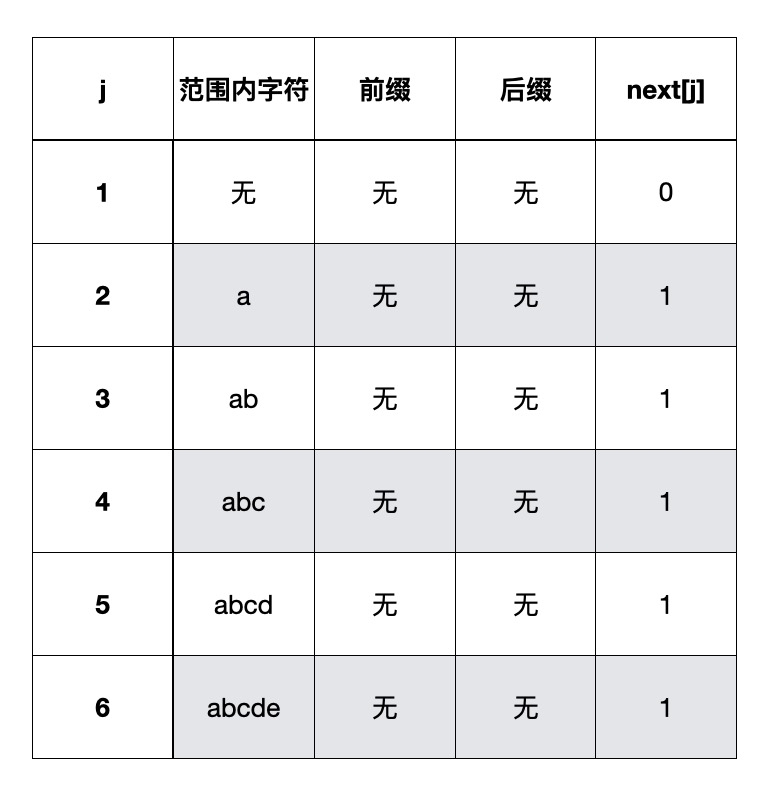
  • “abcdex”结果是[0,1,1,1,1,1]
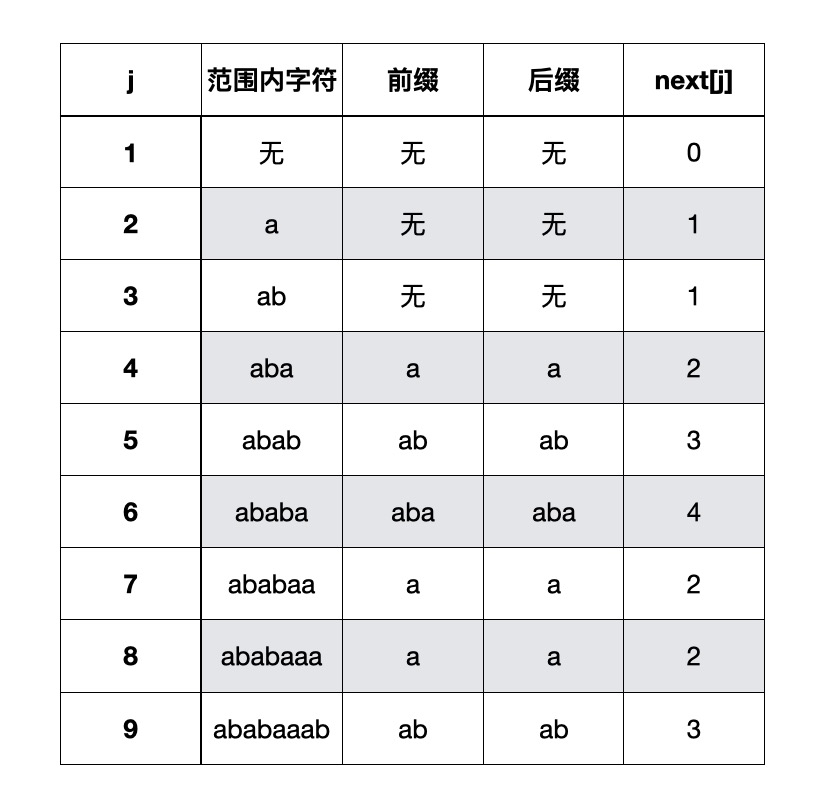
  • “ababaaaba”结果是[0,1,1,2,3,4,2,2,3]
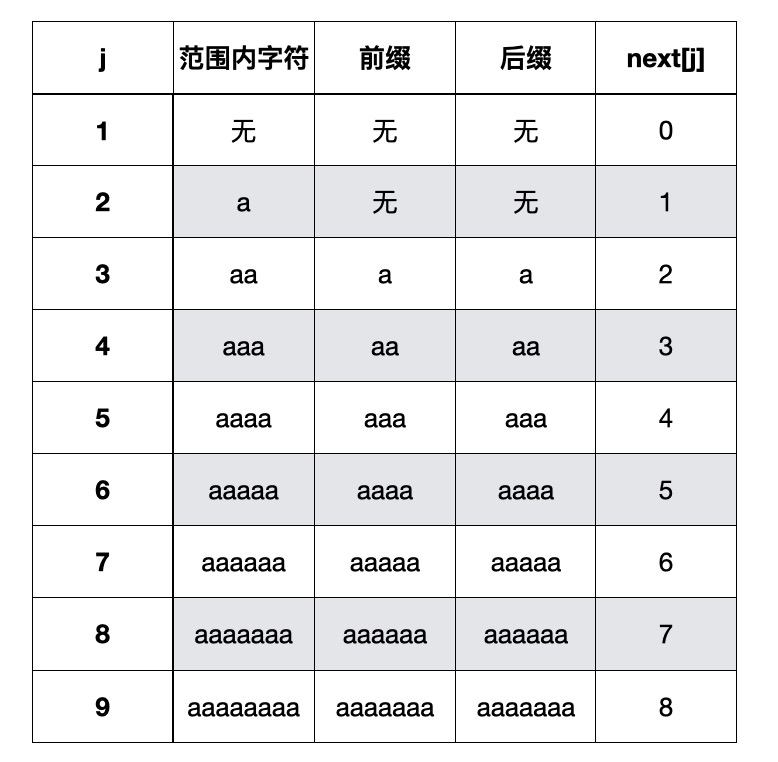
  • “aaaaaaaab”结果是[0,1,2,3,4,5,6,7,8]

代码部分

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100

typedef int Status;
typedef char String[MAXSIZE + 1];

//初始化自定义的字符串
Status createStr(String str, char *c) {
    if (strlen(c) > MAXSIZE) {
        return ERROR;
    }
    
    str[0] = strlen(c);
    for (int i = 1; i <=str[0] ; i++) {
        str[i] = *(c + i - 1);
    }
    return OK;
}
//获取next数组方法
void getNextArr(String str, int *next) {
    int i = 0;
    int j = 1;
    next[1] = 0;
    while (j < str[0]) {
        if (i == 0 || str[i] == str[j]) {
            i++;
            j++;
            next[j] = i;
        } else {
            i = next[i];
        }
    }
}

int index_KMP(String S, String T, int pos) {
    int i = pos;
    int j = 1;
    int next[MAXSIZE];
    getNextArr(T, next);
    while (i <= S[0] && j <= T[0]) {
        if (j == 0 || S[i] == T[j]) {
            i++;
            j++;
        } else {
            j = next[j];
        }
    }
    
    if (j > T[0]) {
        return i - T[0];
    } else {
        return -1;
    }
    
    return -1;
}

KMP优化

举一个和前面类似模式串例子：T="aaaaax"，next[]:{0,1,2,3,4,5}。S="aaaabcde",如图：

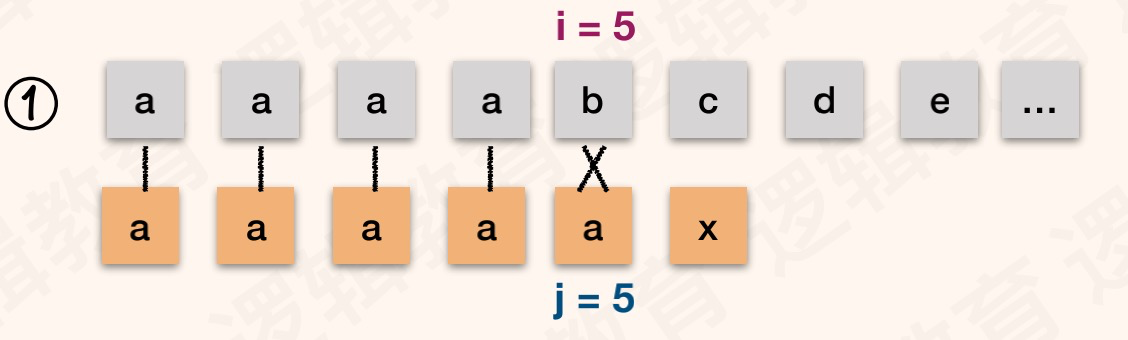
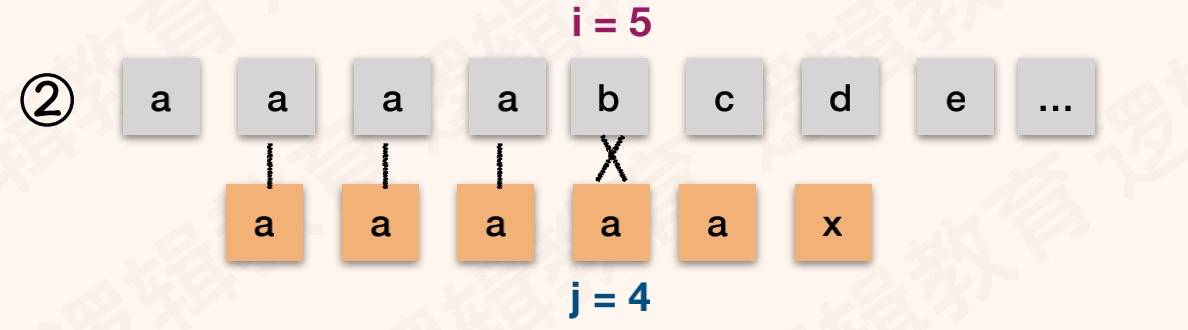
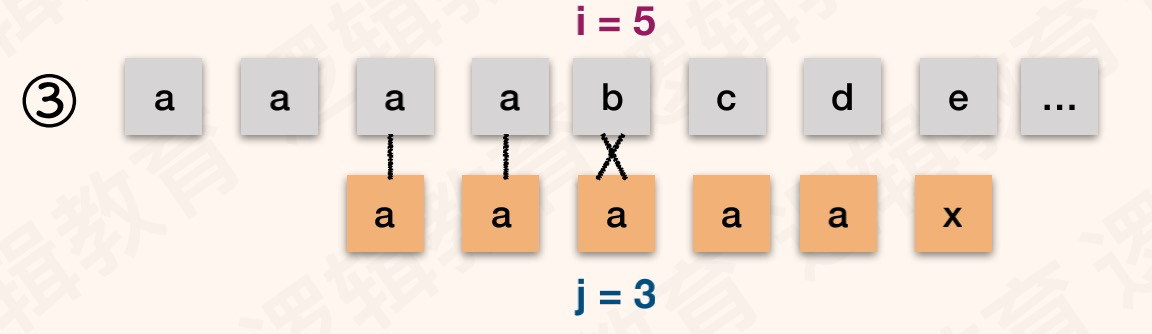
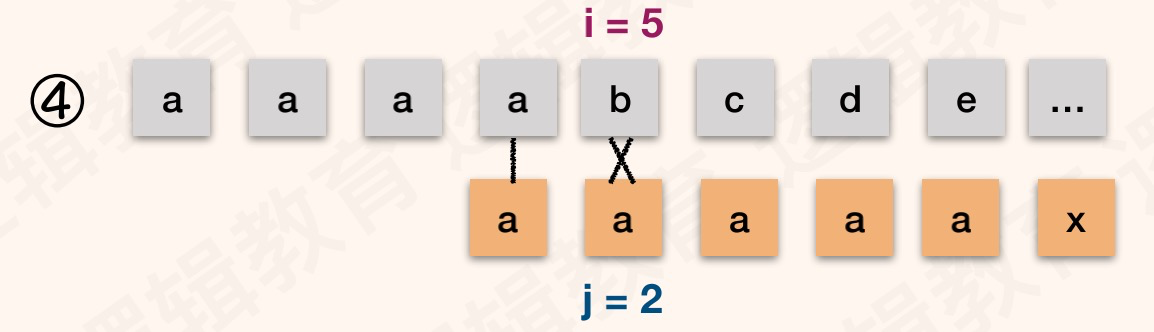
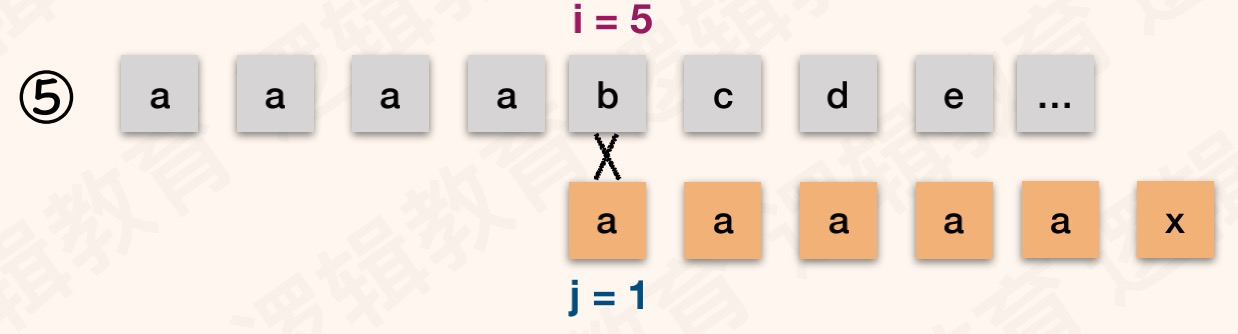
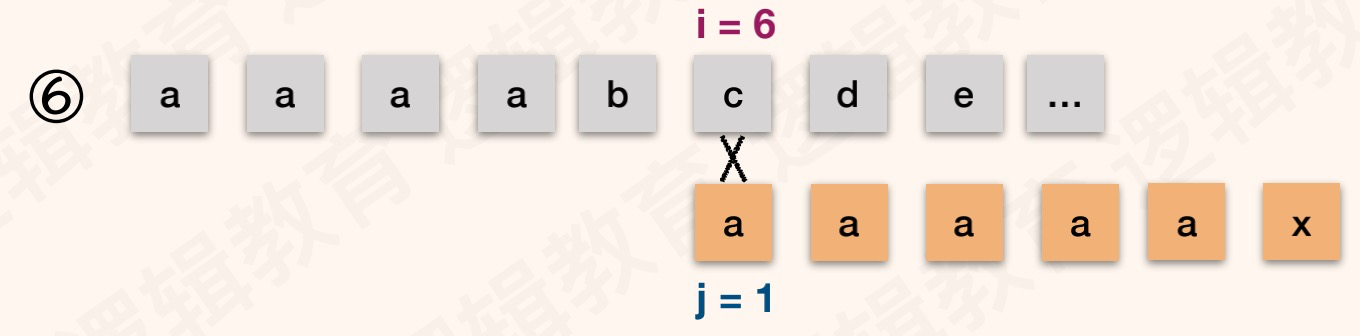
当模式串中存在连续重复的字符时，其实kmp的算法会有一个弊端，在这种特殊情况下，我们可以对回溯数组进行简单的调整，我们给调整后的数组命名为：nextval[j]:
nextval数组创建逻辑是：在模式串中，当前字符与比较的字符相等，则记录为0；字符不等，获取比较字符next数组中的数据。

解读

以T=“ababaaaba”为例，初始状态索引值i=0，遍历值j=1，nextval[1]=0。 与普通模式相比，增加了T[i]和T[j]字符相等判断。如果相等获取i对应的next值；如果不等，保持逻辑不变。

代码

大家可以对照普通模式的代码比较来看

void getNextValArr(String str, int *nextVal) {
    int i = 0;
    int j = 1;
    nextVal[1] = 0;
    while (j < str[0]) {
        if (i == 0 || str[i] == str[j]) {
            i++;
            j++;
            //差异的地方
            if (str[i] == str[j]) {
                nextVal[j] = nextVal[i];
            } else {
                nextVal[j] = i;
            }
        } else {
            i = nextVal[i];
        }
    }
}

int index_KMP1(String S, String T, int pos) {
    int i = pos;
    int j = 1;
    int next[MAXSIZE];
    //函数调用不同
    getNextValArr(T, next);
    while (i <= S[0] && j <= T[0]) {
        if (j == 0 || S[i] == T[j]) {
            i++;
            j++;
        } else {
            j = next[j];
        }
    }
    
    if (j > T[0]) {
        return i - T[0];
    } else {
        return -1;
    }
}

运行

两种方式函数调用

int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, 查找子串!\n");
    
    String P;
    createStr(P, "abcacabdc");
    String T;
    createStr(T, "abd");
    
    int pos = index_KMP(P, T, 1);
    printf("%d\n", pos);
    
    pos = index_KMP1(P, T, 1);
    printf("%d\n", pos);
    
    return 0;
}

总结

这次学习后，有更加深入的了解KMP的原理。虽然之前有过学习，但再一次的学习还会感觉到震惊。这可能就是优秀算法的美丽所在。还有KMP的思想其实很难表达，在我写这篇文章的时候，脑中想的东西也很难转换成文字和图片。文章的结束不代表我对KMP算法学习的结束，以后如果有更好的想法和思路去阐述KMP的原理实现，我会对这篇文章进行更新。

avatar
文章
阅读
粉丝