基本数据结构 - Queue(队列)队列数据结构是先进先出原则（FIFO first-in first-out）。比如我

队列数据结构是先进先出原则（FIFO first-in first-out）。比如我们使用GCD向队列添加任务就是如此。在实际生活中的排队行为也是如此，先排队的先处理。下面探讨的是一些实现队列数据结构的方式以及它们的性能对比。

基本操作

首先先创建一个队列的协议

public protocol Queue {
    
    associatedtype Element
    
    mutating func enqueue(_ element: Element) -> Bool
    
    mutating func dequeue() -> Element?
    
    var isEmpty: Bool { get }
    
    var peek: Element? { get }
}

协议定义了队列的基本操作

enqueue: 入队，在队列末尾插入元素，如果插入成功返回true。
dequeue: 出队，从队列前面移除元素并且返回该元素。
isEmpty: 判断队列是否为空。
peek: 返回队列前面的元素，但是不移除。

一个队列只对头部和末尾的有实际的数据操作。

在下面的代码中我们会使用4种不同方式实现队列数据结构并分析起性能差异

使用数组形式实现队列（下面统称为 数组队列）
使用双向链表形式实现队列（下面统称为 链表队列）
使用环形缓冲区形式实现队列（下面统称为 环型缓冲区队列）
使用两个栈形式实现队列（下面统称为 栈队列）
数组队列的实现

数组数据结构里面的元素在内存里面是有序的并且连续存储的。

定义头部实现

public struct QueueArray<T>: Queue {
    
    // 使用数组存储实现队列数据结构
    private var array: [T] = []
    
    public init() {}
    
}

由于我们在上面的队列协议中定义了一个关联类型 Element，Swift在 QueueArray<T>: Queue 会知道此时的关联类型是 T。下面我们会添加协议实现。

使用数组基本特性

    public var isEmpty: Bool {
        return array.isEmpty
    }
    
    public var peek: T? {
        return array.first
    }

协议isEmpty的实现直接使用了数组的isEmpty属性判断，协议peek直接返回数组第一个元素。两个操作的时间复杂度都是 O(1)

enqueue（入队）

    public mutating func enqueue(_ element: T) -> Bool {
        array.append(element)
        return true
    }

在数组数据结构中，如果一个数组里面已经填满元素，如果此时再次向里面添加元素会导致数组内存空间直接扩充一倍。如下图所示添加 Eric 的结果：

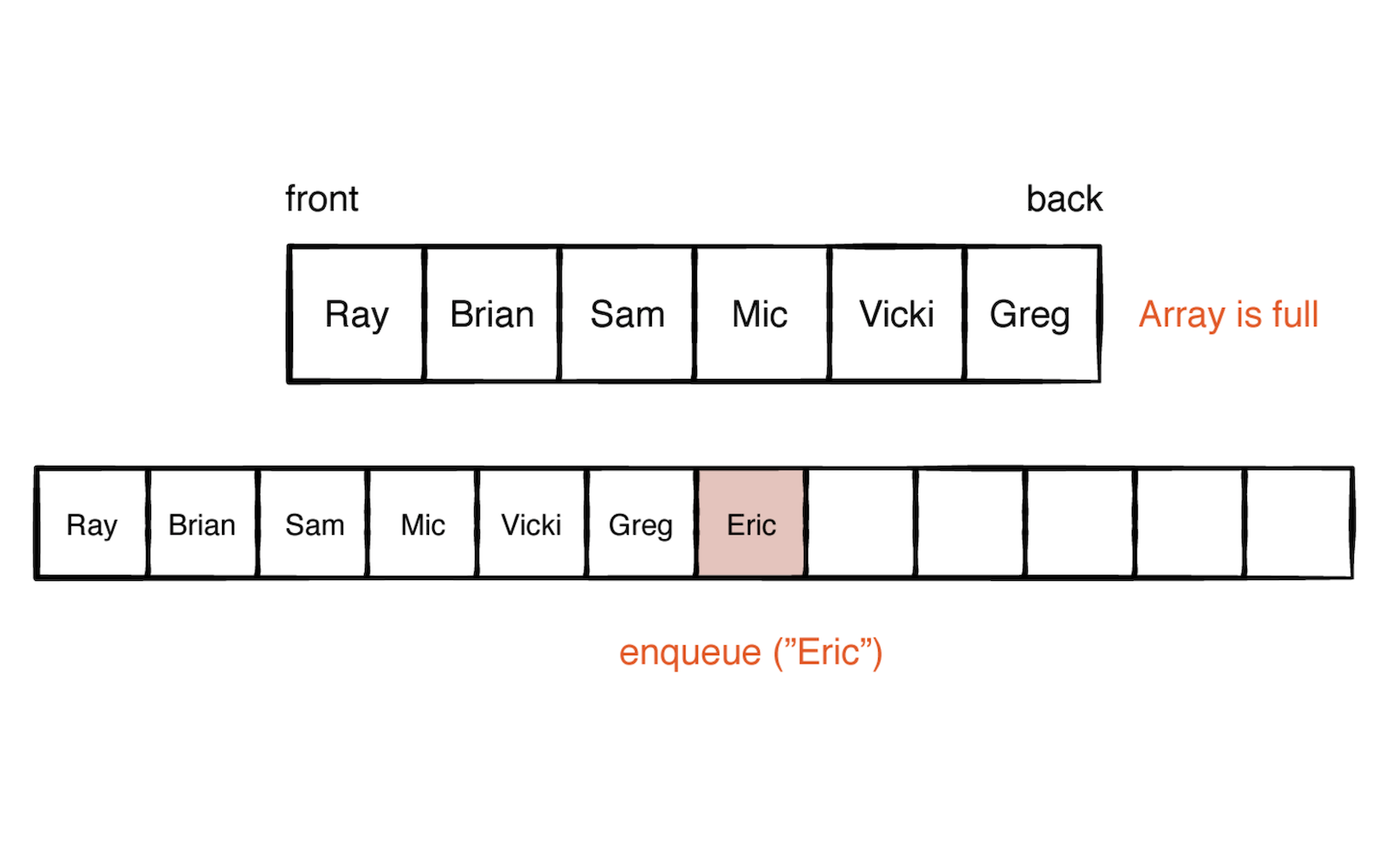
所以在好的情况入队一个元素的时间复杂度是 O(1)。坏的情况下比如此时数组内存空间已经填满，那么入队一个元素，数组内存空间扩充一倍，时间复杂度就是 O(n) 。但是数组内存空间扩充一倍的情况毕竟还是少数，所以总体入队的时间复杂度为 O(1)。

dequeue（出队）

    public mutating func dequeue() -> T? {
        isEmpty ? nil : array.removeFirst()
    }

先判断队列是否为空，为空返回nil，否则移除数组第一个元素。在数组内存结构中，由于数组里面的元素是有序的连续内存分布的。此时移除第一个内存元素会导致后面所有内存里面的元素都前向移动一位。

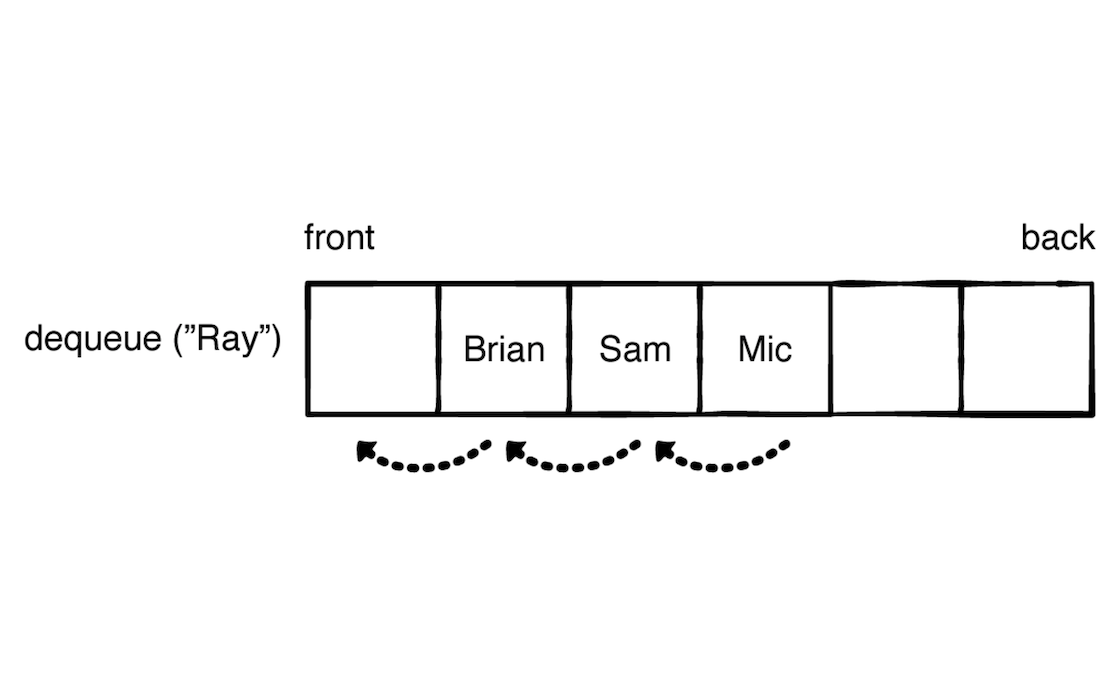
所以出队操作的时间复杂度是 O(n)。

Debug 和测试

添加一个测试辅助:

extension QueueArray: CustomStringConvertible {
    public var description: String {
        String(describing: array)
    }
}

测试：

var queue = QueueArray<String>()
queue.enqueue("C")
queue.enqueue("Swift")
queue.enqueue("Objective-C")

print("Queue: \(queue)")

queue.dequeue()
print("After dequeue, Queue: \(queue)")

queue.peek
print("After peek, Queue: \(queue)")

输出：

Queue: ["C", "Swift", "Objective-C"]
After dequeue, Queue: ["Swift", "Objective-C"]
After peek, Queue: ["Swift", "Objective-C"]

优缺点分析

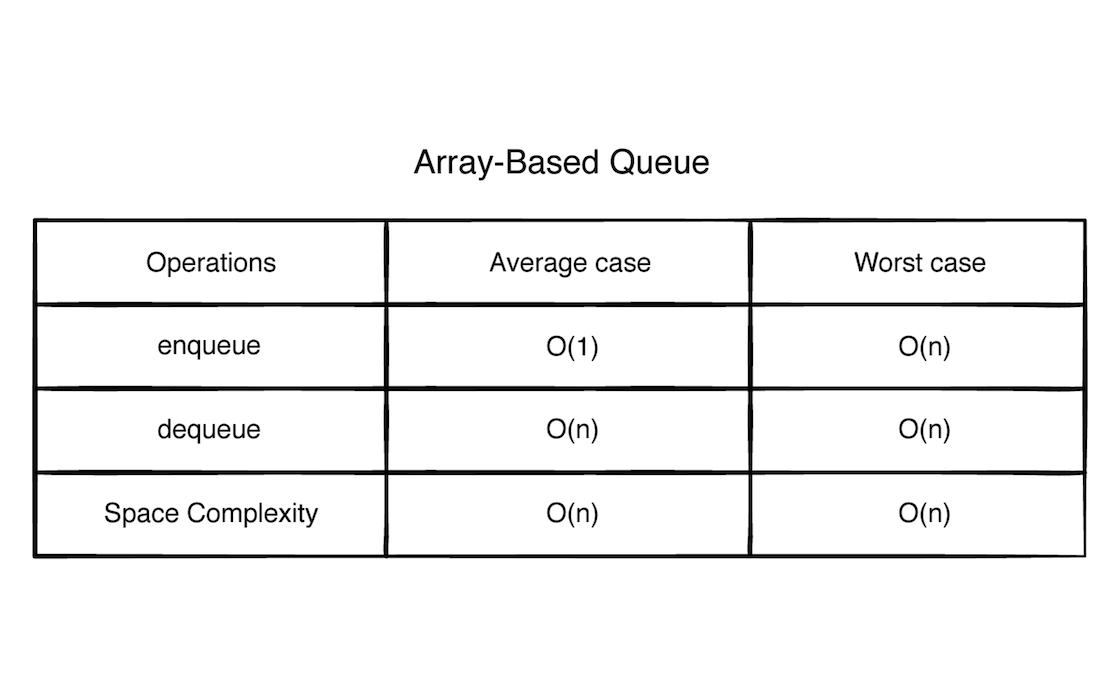
如图所以

使用数组实现的方式入队操作的时间复杂度平均情况为 O(1), 最坏情况为 O(n)。如果此时数组里面的内存空间已经很大了，那么最坏情况是会加倍内存空间的。

因为里面的数据存储是数组，出队的时间复杂度平均情况和最坏情况都是 O(n)。每次出队操作都会把后面的所有元素前向移动一位，如果数据量庞大，这会消耗非常大的性能。

空间复杂度的平均的情况和最坏情况都是 O(n)。

数组数据结构形式虽然可以很容易实现队列效果，但是总体性能不是很好，下面我们来看看链表队列的实现。

链表队列的实现

单向链表数据结构的实现：基本数据结构 - Linked List(链表)。正常情况链表是只有上一个节点指向下一个节点的，比如节点A指向节点B，节点B不能指向节点A，里面的数据结构是单方向的。双向链表数据结构如它的名字所示就是双向的了，节点A和节点B互相都有指向。

双向链表 DoublyLinkedList 实现：

public class Node<T> {
    
    public var value: T
    public var next: Node<T>?
    public var previous: Node<T>?
    
    public init(value: T) {
        self.value = value
    }
}

extension Node: CustomStringConvertible {
    
    public var description: String {
        String(describing: value)
    }
}

public class DoublyLinkedList<T> {
    
    private var head: Node<T>?
    private var tail: Node<T>?
    
    public init() { }
    
    public var isEmpty: Bool {
        head == nil
    }
    
    public var first: Node<T>? {
        head
    }
    
    public func append(_ value: T) {
        let newNode = Node(value: value)
        
        guard let tailNode = tail else {
            head = newNode
            tail = newNode
            return
        }
        
        newNode.previous = tailNode
        tailNode.next = newNode
        tail = newNode
    }
    
    public func remove(_ node: Node<T>) -> T {
        let prev = node.previous
        let next = node.next
        
        if let prev = prev {
            prev.next = next
        } else {
            head = next
        }
        
        next?.previous = prev
        
        if next == nil {
            tail = prev
        }
        
        node.previous = nil
        node.next = nil
        
        return node.value
    }
}

extension DoublyLinkedList: CustomStringConvertible {
    
    public var description: String {
        var string = ""
        var current = head
        while let node = current {
            string.append("\(node.value) -> ")
            current = node.next
        }
        return string + "end"
    }
}

public class LinkedListIterator<T>: IteratorProtocol {
    
    private var current: Node<T>?
    
    init(node: Node<T>?) {
        current = node
    }
    
    public func next() -> Node<T>? {
        defer { current = current?.next }
        return current
    }
}

extension DoublyLinkedList: Sequence {
    
    public func makeIterator() -> LinkedListIterator<T> {
        LinkedListIterator(node: head)
    }
}

添加双向链表队列 QueueLinkedList ：

public class QueueLinkedList<T>: Queue {
    
    private var list = DoublyLinkedList<T>()
    public init() {}
}

在这个链表队列里面直接使用了 DoublyLinkedList 双向链表数据结构作为元素的存储。

enqueue（入队）

    public func enqueue(_ element: T) -> Bool {
        list.append(element)
        return true
    }

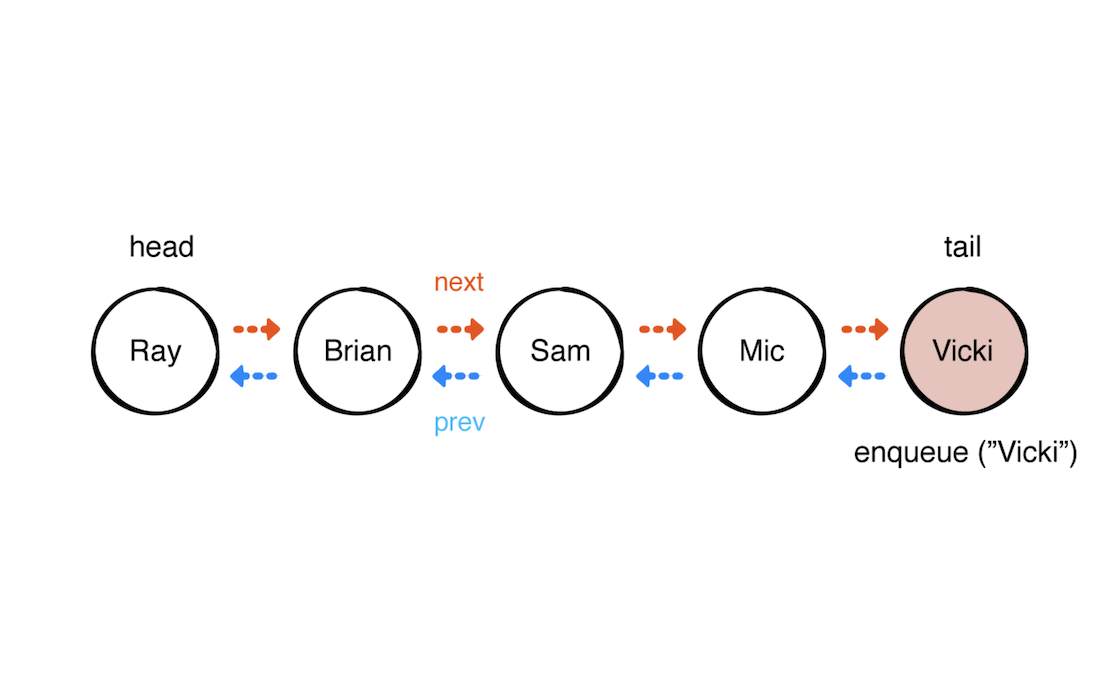
如图所示，入队Vicki，双向链表list直接添加数据，更新里面的引用。时间复杂度为 O(1)。

dequeue（出队）

    public func dequeue() -> T? {
        guard !list.isEmpty, let element = list.first else {
            return nil
        }
        return list.remove(element)
    }

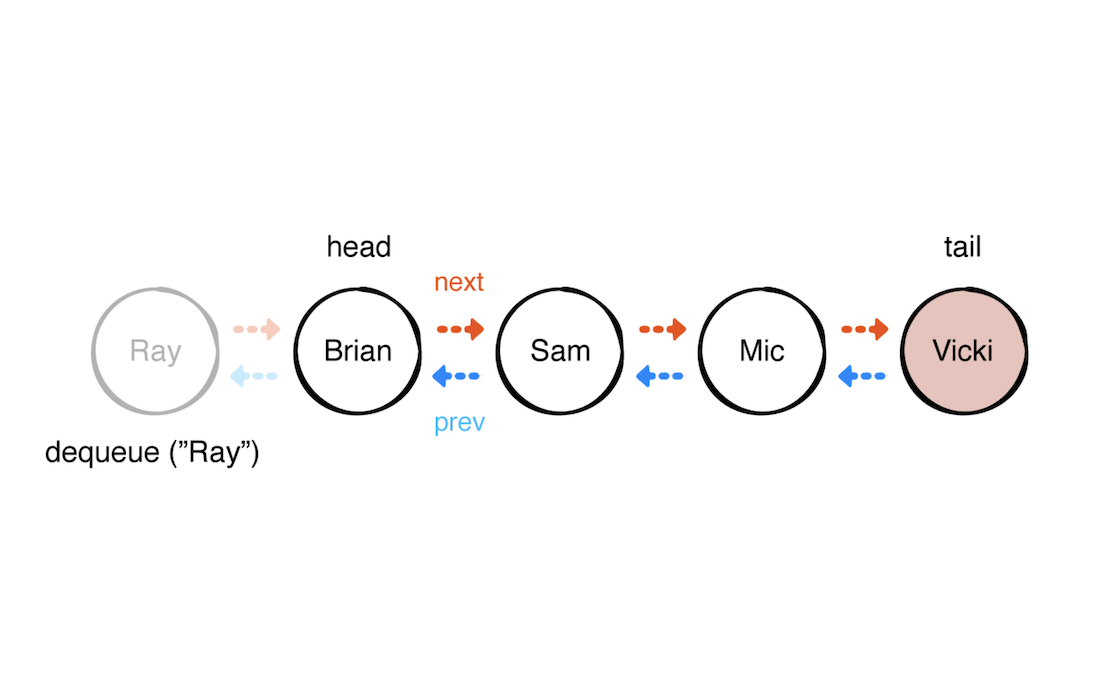
如图所示，出队Ray，双向链表list直接移除数据，更新里面的引用。时间复杂度为 O(1)。与上面的数组形式实现队列相比，此时不用把所以数据都前向移动一位了，只需要更新一下head 的引用即可。

实现 peek 和 isEmpty

    public var peek: T? {
        list.first?.value
    }
    
    public var isEmpty: Bool {
        list.isEmpty
    }

Debug 和测试

添加一个测试辅助:

extension QueueLinkedList: CustomStringConvertible {
    
    public var description: String {
        String(describing: list)
    }
}

测试：

var queue = QueueLinkedList<String>()
queue.enqueue("C")
queue.enqueue("Swift")
queue.enqueue("Objective-C")

print("Queue: \(queue)")

queue.dequeue()
print("After dequeue, Queue: \(queue)")

queue.peek
print("After peek, Queue: \(queue)")

输出：

Queue: C -> Swift -> Objective-C -> end
After dequeue, Queue: Swift -> Objective-C -> end
After peek, Queue: Swift -> Objective-C -> end

优缺点分析

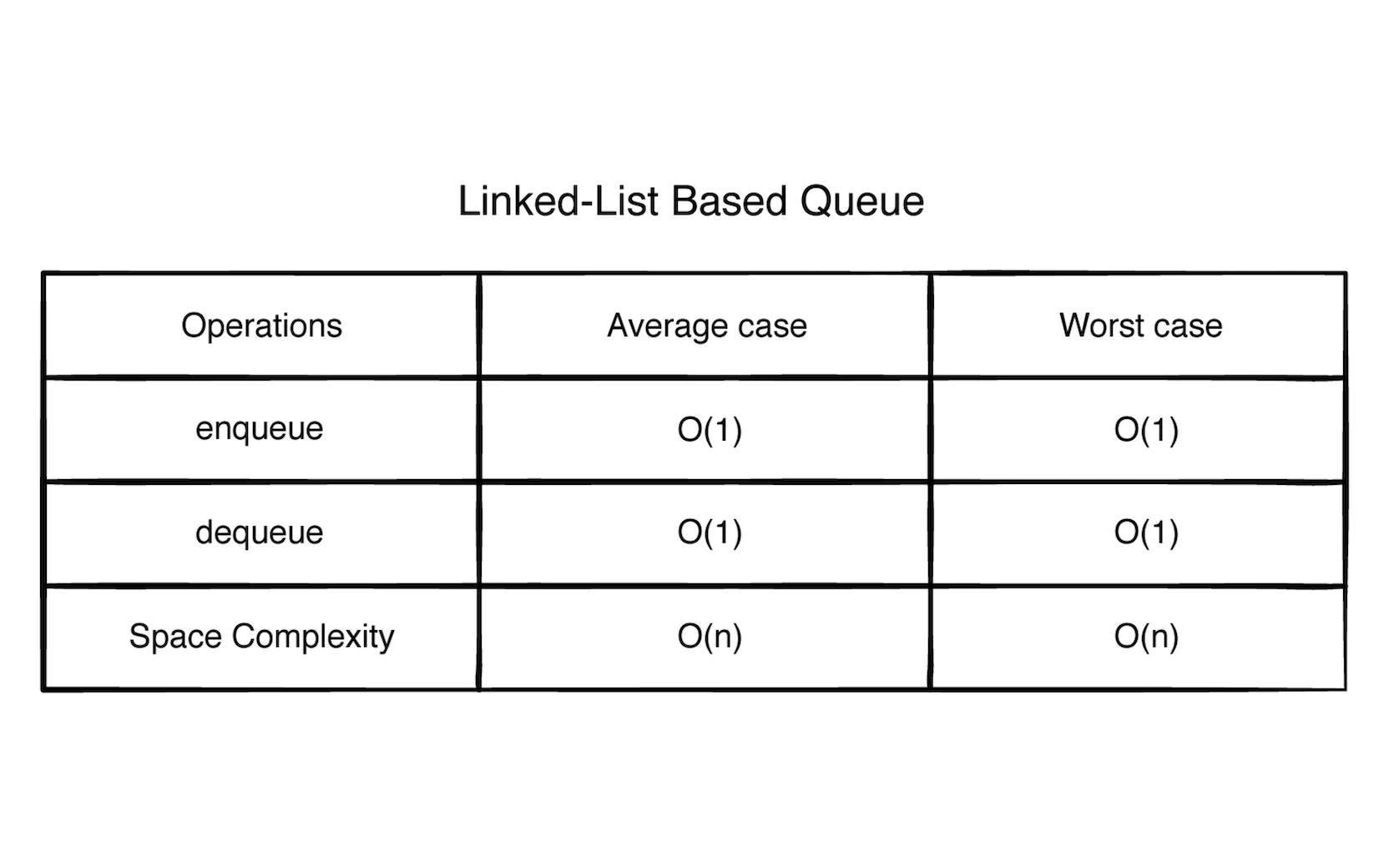
优点是链表方式实现队列的出队和入队都是 O(1) 操作。它的缺点在这看起来不是很明显，但是每个元素的创建里面的引用是双向的，这增加了一些其它额外的开销。而且每个元素的创建都是一些动态创建开销，而对于数组方式形式实现的情况来说，数组能很好的管理内在的元素。

如果能解决元素创建成本高的问题，但是能保证操作都是 O(1) 的就好了，下面我们看环型缓冲区队列的实现。

环型缓冲区队列的实现

环形缓冲区也可以叫做循环缓冲区，里面是一个固定元素数目的数组。这个数据结构的策略是当数组最后面的元素没有可以移除了的时候，指向的位置重置到数组开头。

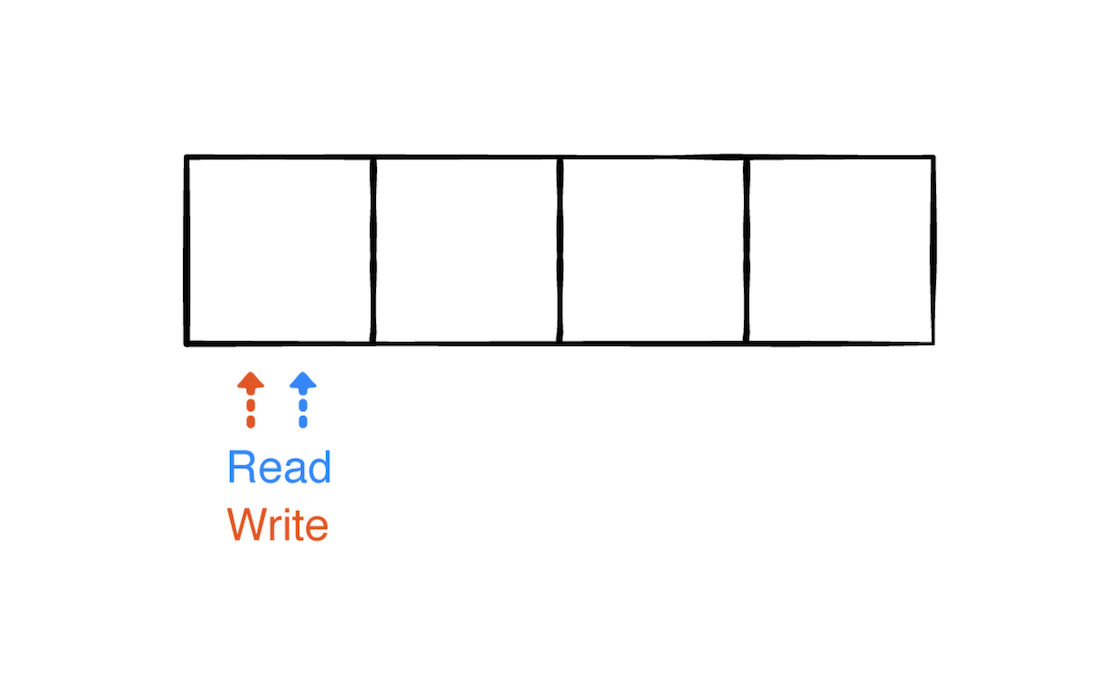
如图所示，创建了一个尺寸为4的环型缓冲区。里面有两个指针。

read 读指针。
write 写指针。

write 操作指向哪一块表明哪一块需要是下一个被写入的位置，read 指针指向哪一个位置，表明那个位置是要被读取的位置。

入队一个元素是这样的：

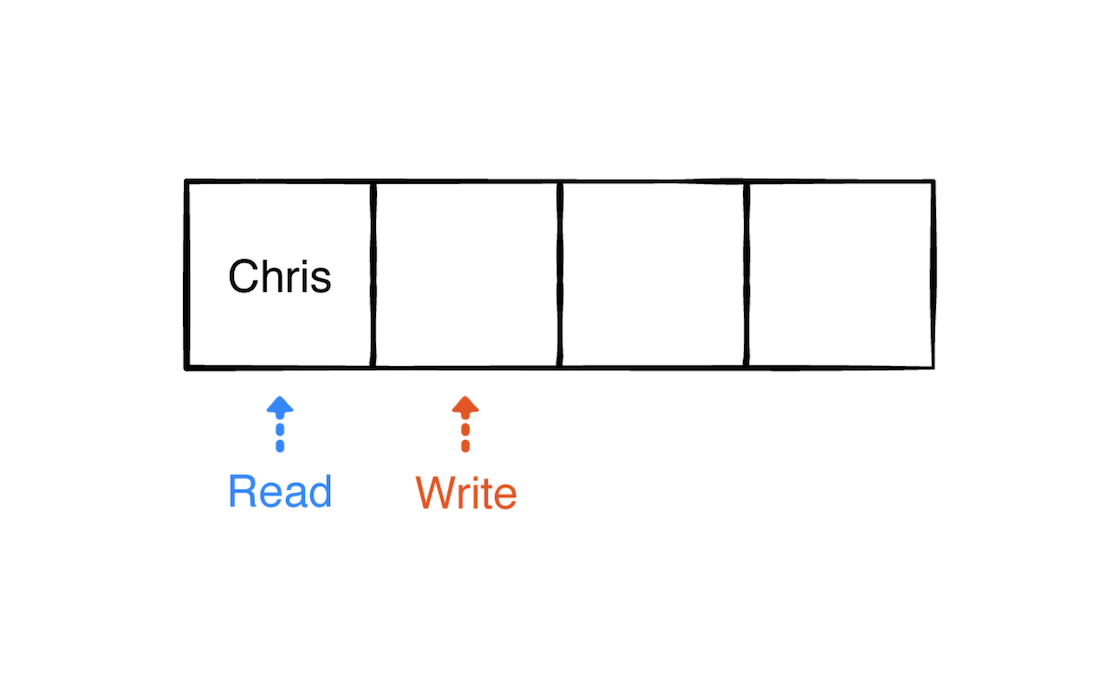
每次入队一个元素到队列都会把 write 指针下移一位。下面入队更多元素：

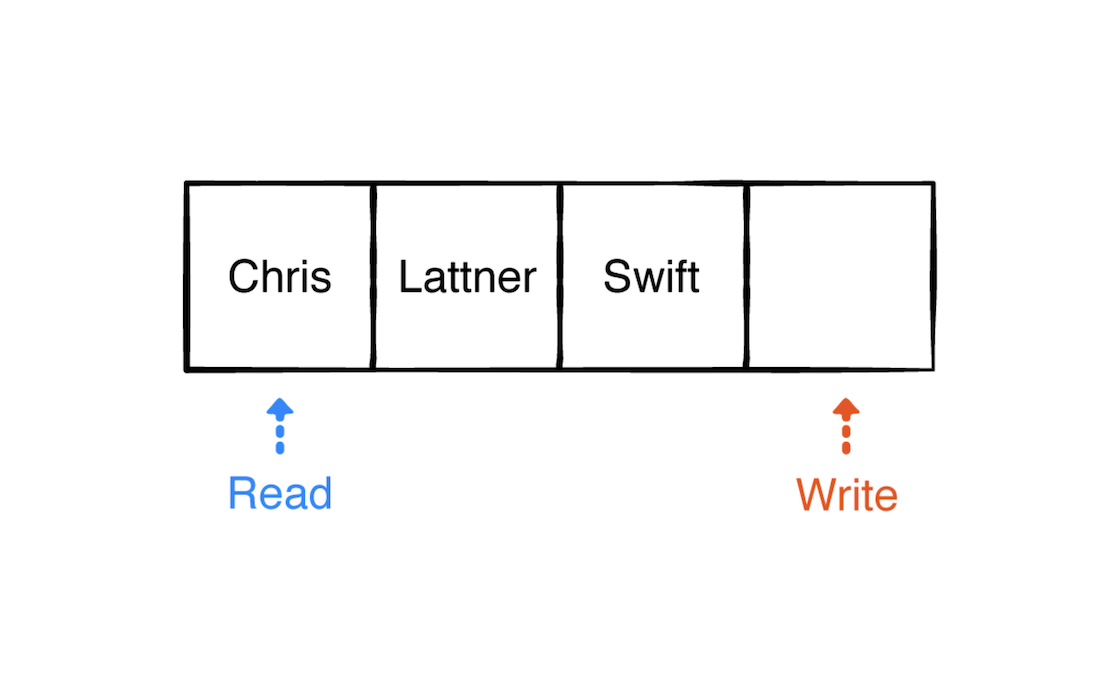
下一步，出队两个元素：

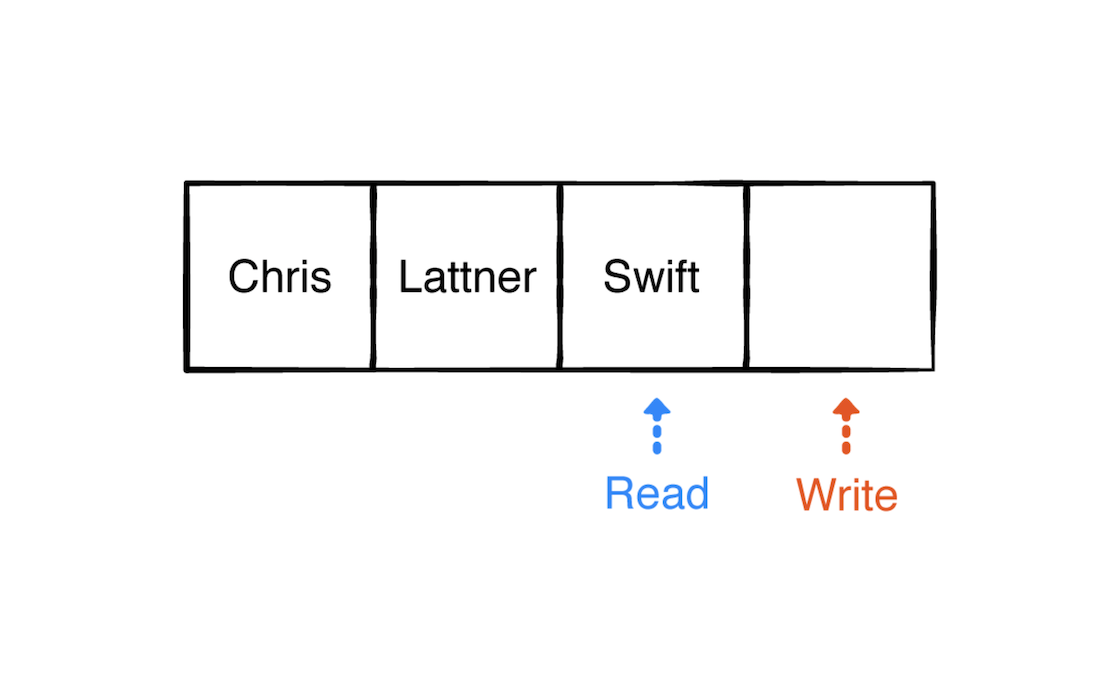
可以看到出队和入队的操作是类似的。

下面再次入队一个元素：

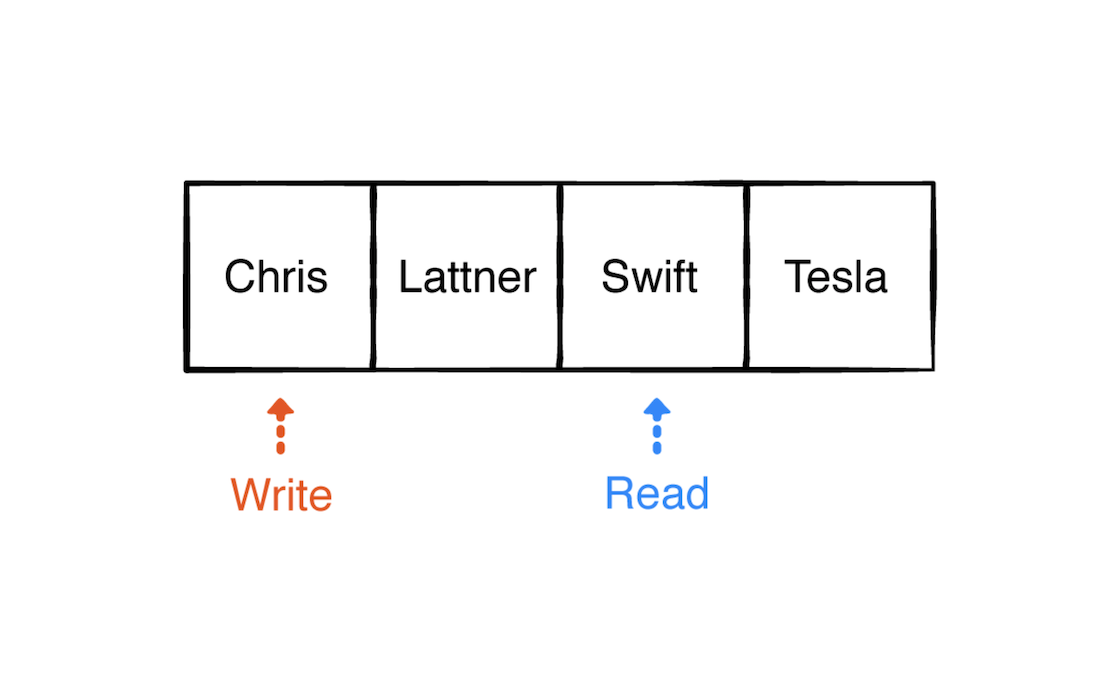
由于入队操作已经到了尾部，所以write指针重新回到开始处，这也就是为什么叫做环形缓冲区了。

最后出队最后两个元素：

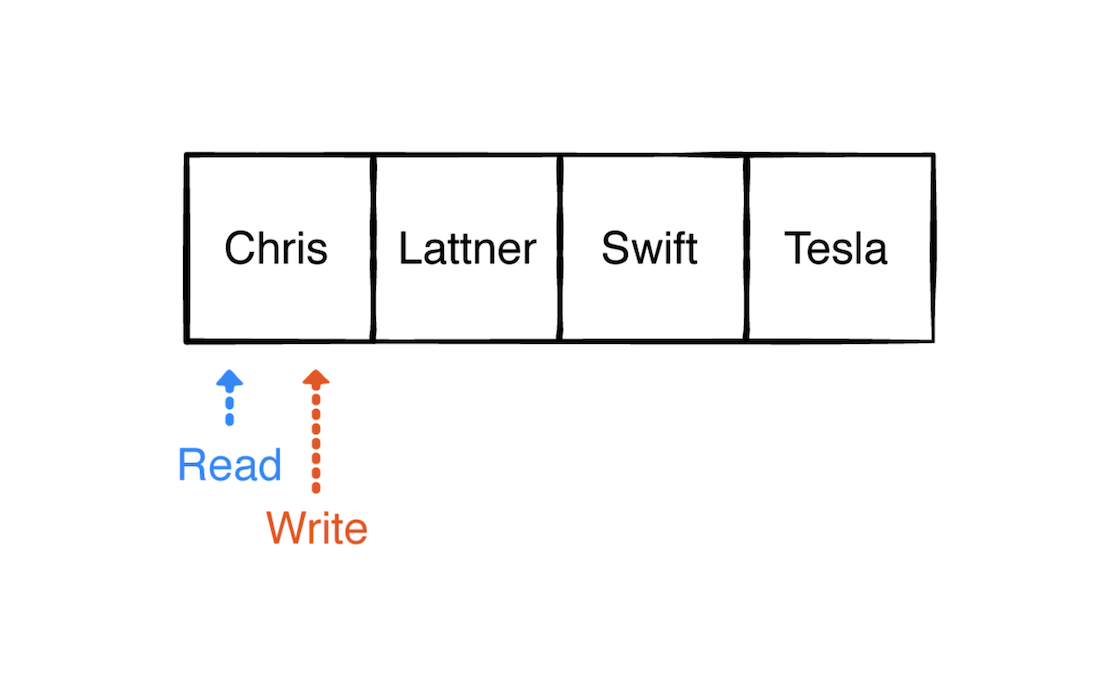
此时read指针也回到了初始位置。当read指针和write指针都指向同个位置时，此时意味着队列为空。

下面添加一个环形缓冲区实现。

public struct RingBuffer<T> {
    
    private var array: [T?]
    private var readIndex = 0
    private var writeIndex = 0
    
    public init(count: Int) {
        array = Array<T?>(repeating: nil, count: count)
    }
    
    public var first: T? {
        array[readIndex]
    }
    
    public mutating func write(_ element: T) -> Bool {
        if !isFull {
            array[writeIndex % array.count] = element
            writeIndex += 1
            return true
        } else {
            return false
        }
    }
    
    public mutating func read() -> T? {
        if !isEmpty {
            let element = array[readIndex % array.count]
            readIndex += 1
            return element
        } else {
            return nil
        }
    }
    
    private var availableSpaceForReading: Int {
        writeIndex - readIndex
    }
    
    public var isEmpty: Bool {
        availableSpaceForReading == 0
    }
    
    private var availableSpaceForWriting: Int {
        array.count - availableSpaceForReading
    }
    
    public var isFull: Bool {
        availableSpaceForWriting == 0
    }
}

extension RingBuffer: CustomStringConvertible {
    public var description: String {
        let values = (0..<availableSpaceForReading).map {
            String(describing: array[($0 + readIndex) % array.count]!)
        }
        return "[" + values.joined(separator: ", ") + "]"
    }
}

里面的实现逻辑其实也很简单。就是使用一个固定元素数目的数组数据结构管理里面的元素。如果你对这个缓冲区的更多实现方式感兴趣，可以查看： github.com/raywenderli…。

队列的环形缓冲区实现:

public class QueueRingBuffer<T>: Queue {
    
    private var ringBuffer: RingBuffer<T>
    
    init(count: Int) {
        ringBuffer = RingBuffer<T>(count: count)
    }
    
    public var isEmpty: Bool {
        return ringBuffer.isEmpty
    }
    
    public var peek: T? {
        return ringBuffer.first
    }
    
}

在初始化的时候传入了一个count参数是为了确定里面数组的元素数目。isEmpty 和 peek 操作的时间复杂度都是 O(1)。

enqueue（入队）

    public mutating func enqueue(_ element: T) -> Bool {
        ringBuffer.write(element)
    }

O(1) 操作

dequeue（出队）

    public mutating func dequeue() -> T? {
        ringBuffer.read()
    }

O(1) 操作

Debug 和测试

添加一个测试辅助:

extension QueueRingBuffer: CustomStringConvertible {
    public var description: String {
        String(describing: ringBuffer)
    }
}

测试：

var queue = QueueRingBuffer<String>(count: 10)
queue.enqueue("C")
queue.enqueue("Swift")
queue.enqueue("Objective-C")

print("Queue: \(queue)")

queue.dequeue()
print("After dequeue, Queue: \(queue)")

queue.peek
print("After peek, Queue: \(queue)")

输出：

Queue: [C, Swift, Objective-C]
After dequeue, Queue: [Swift, Objective-C]
After peek, Queue: [Swift, Objective-C]

其实和上面两种实现方式的输出是一样的。

优缺点分析

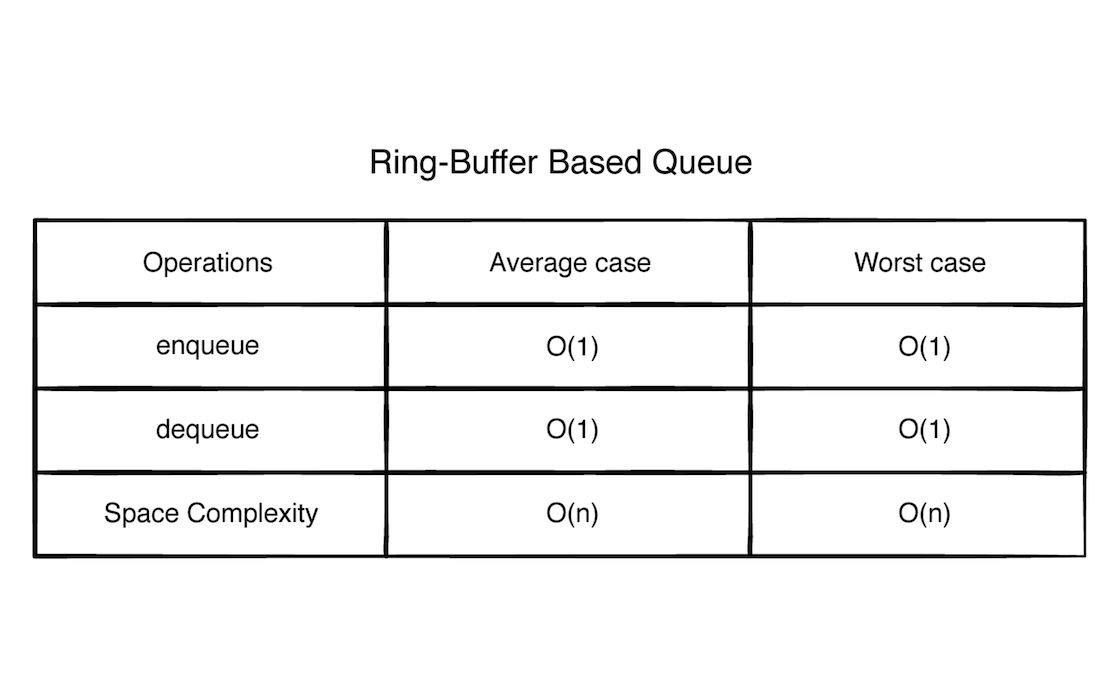
它的出队和入队操作的时间复杂度其实和上面的链表形式实现一样。但是环型缓冲区里面的元素数目是固定的，所以有时候写操作可能失败。

下面我们看栈队列的实现。

栈队列的实现

定义一个基本实现：

public struct QueueStack<T>: Queue {
    
    private var leftStack: [T] = []
    private var rightStack: [T] = []
    
    public init() { }

}

里面的思想是入队的元素进入 rightStack，出队的元素把rightStack里面的元素倒序插入leftStack。这样就实现了队列的 FIFO 原则。

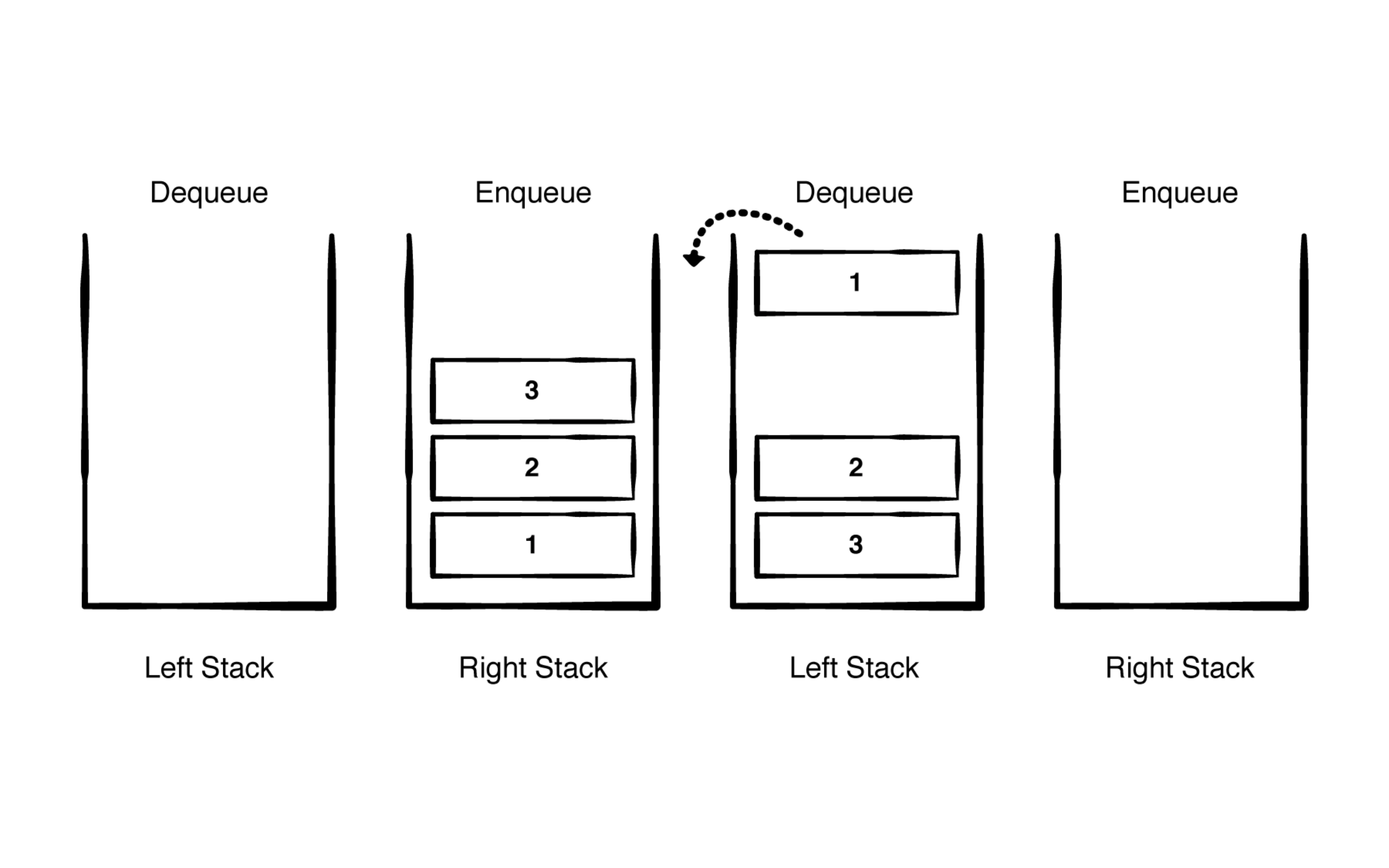
使用数组特性

    public var isEmpty: Bool {
        return leftStack.isEmpty && rightStack.isEmpty
    }
    
    public var peek: T? {
        !leftStack.isEmpty ? leftStack.last : rightStack.first
    }

实现的 isEmpty 和 peek 协议内容也很简单，直接判断里面的两个数组内容就好了。它们的操作都是 O(1)

enqueue（入队）

     public mutating func enqueue(_ element: T) -> Bool {
        rightStack.append(element)
        return true
    }

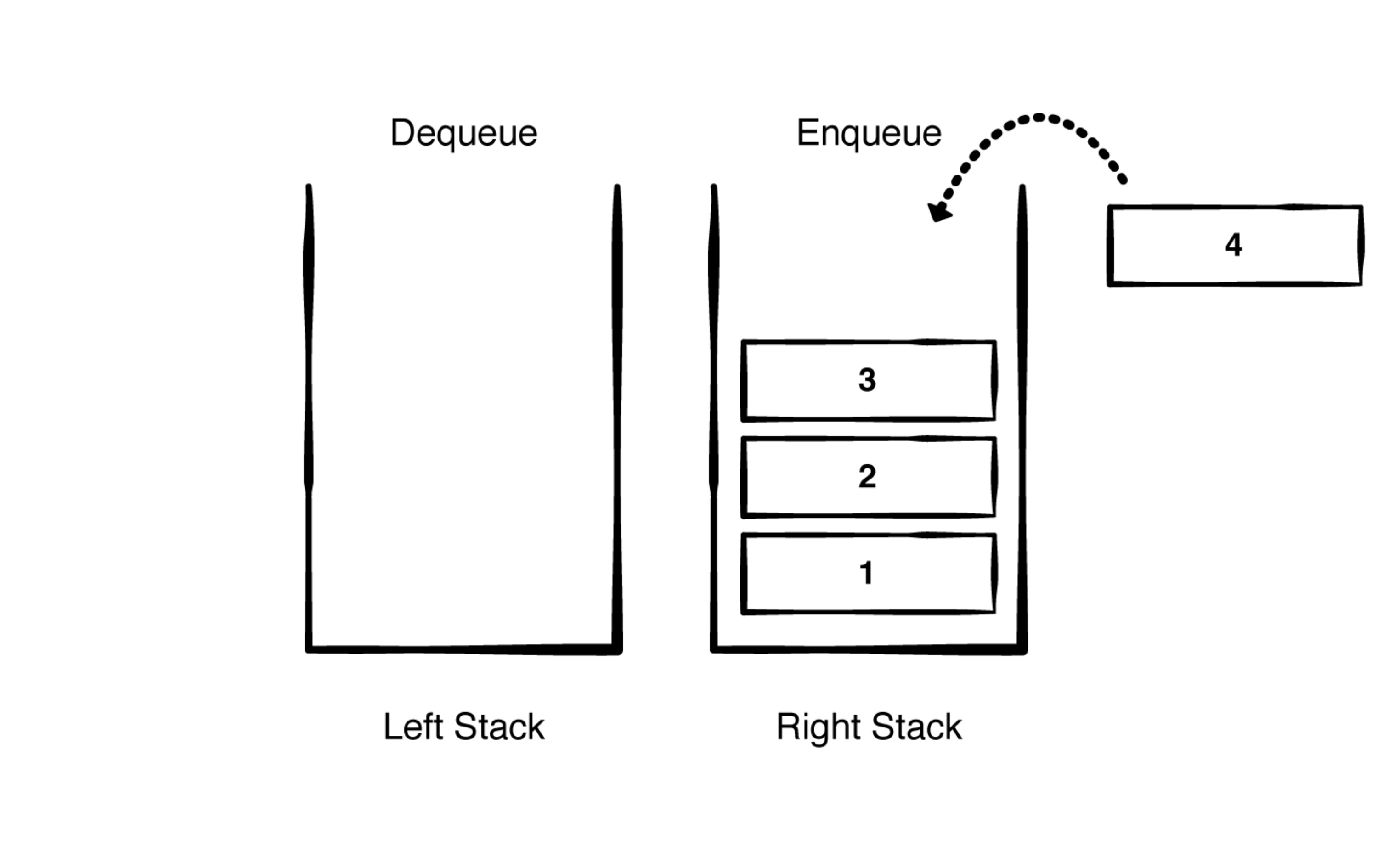
O(1) 操作

dequeue（出队）

      public mutating func dequeue() -> T? {
        // 如果出队数组为空，则引用入队数组里面的倒序数组数据
        if leftStack.isEmpty {
            leftStack = rightStack.reversed()
            rightStack.removeAll()
        }
        
        return leftStack.popLast()
    }

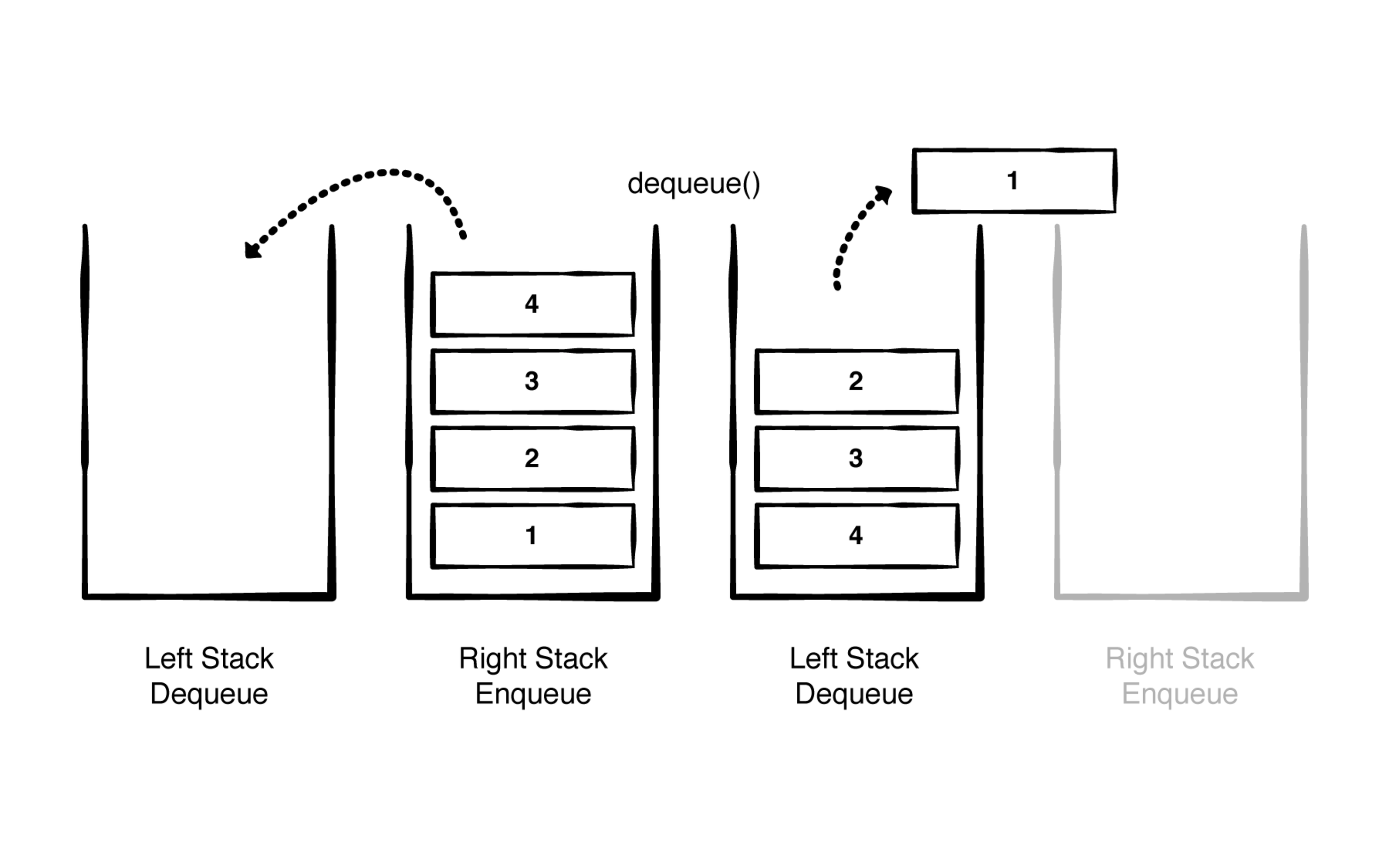
虽然上面的 rightStack.reversed() 操作的时间复杂度是 O(n)，但是对于整个队列来说，它的时间复制度还是为 O(1)（毕竟对于整个数据结构来说 rightStack.reversed() 操作发生的次数还是相对较少的）。

Debug 和测试

添加一个辅助:

extension QueueStack: CustomStringConvertible {
    public var description: String {
        String(describing: leftStack.reversed() + rightStack)
    }
}

测试：

var queue = QueueStack<String>()
queue.enqueue("C")
queue.enqueue("Swift")
queue.enqueue("Objective-C")

print("Queue: \(queue)")

queue.dequeue()
print("After dequeue, Queue: \(queue)")

queue.peek
print("After peek, Queue: \(queue)")

输出：

Queue: [C, Swift, Objective-C]
After dequeue, Queue: [Swift, Objective-C]
After peek, Queue: [Swift, Objective-C]

优缺点分析

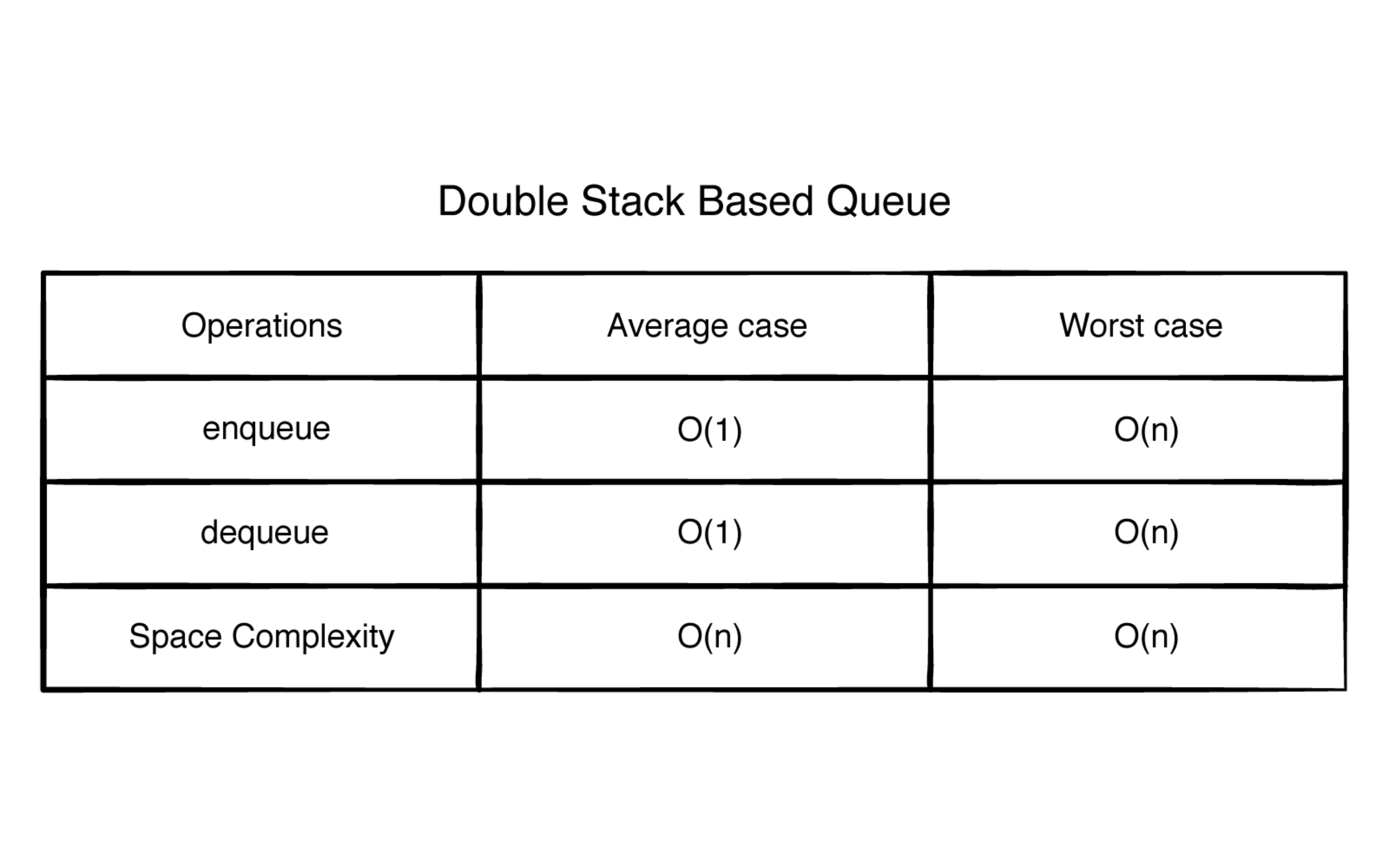
首先入队和出队操作的平均时间复杂度是 O(1), 最坏情况是 O(n)，但是最坏情况比较少发生。再有就是和环型缓冲区相比，它不用固定里面元素的个数，它的动态性更强。

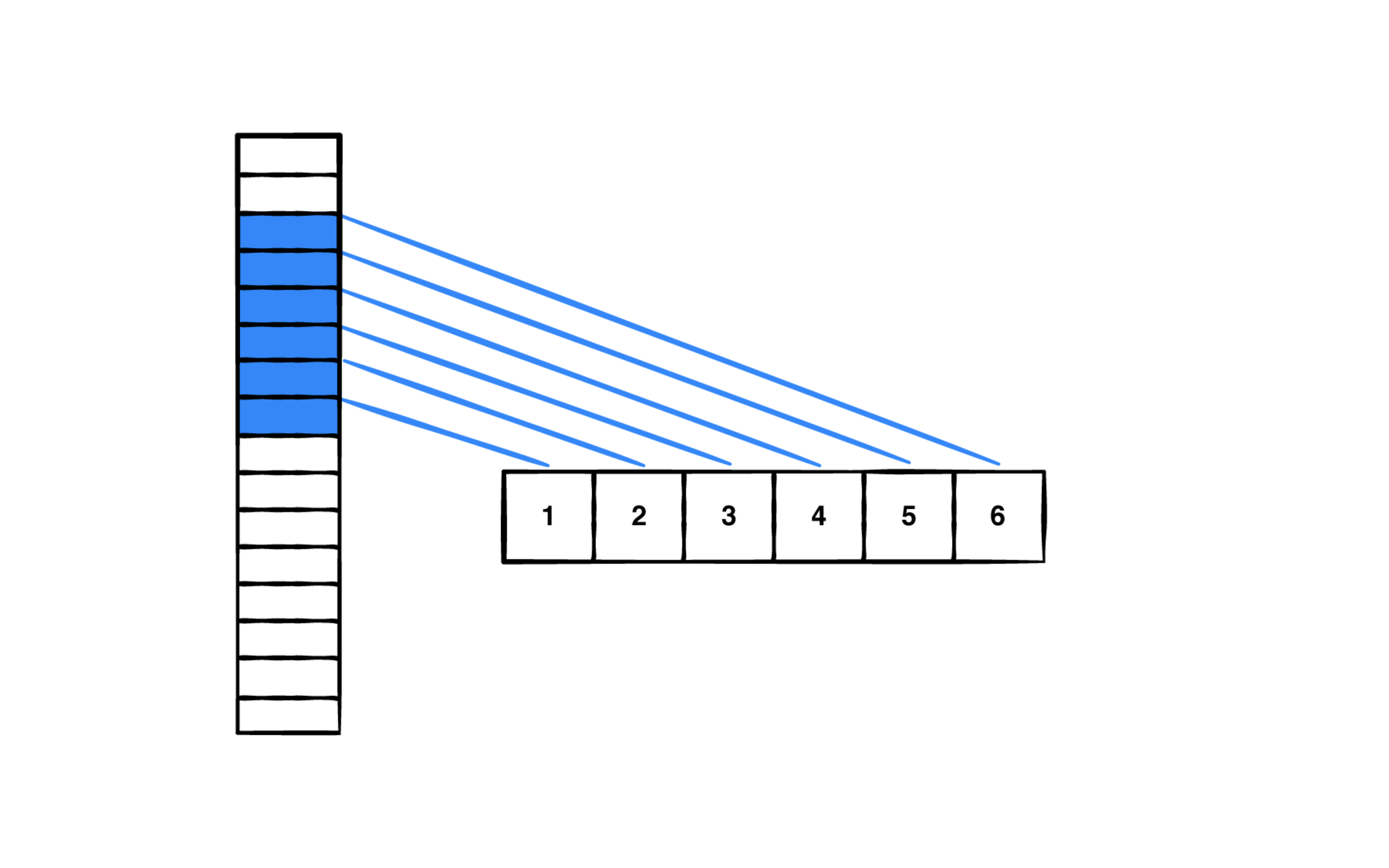
而且里面元素的是数组的内存管理形式，这比链表的内存管理形式好多了。由于链表里面元素的内存地址是分散的，这会导致产生大量的内存浪费。而数组里面的元素是连续分布的，这能很好的管理内存的分配和使用问题。

数组内存结构：

链表内存结构：

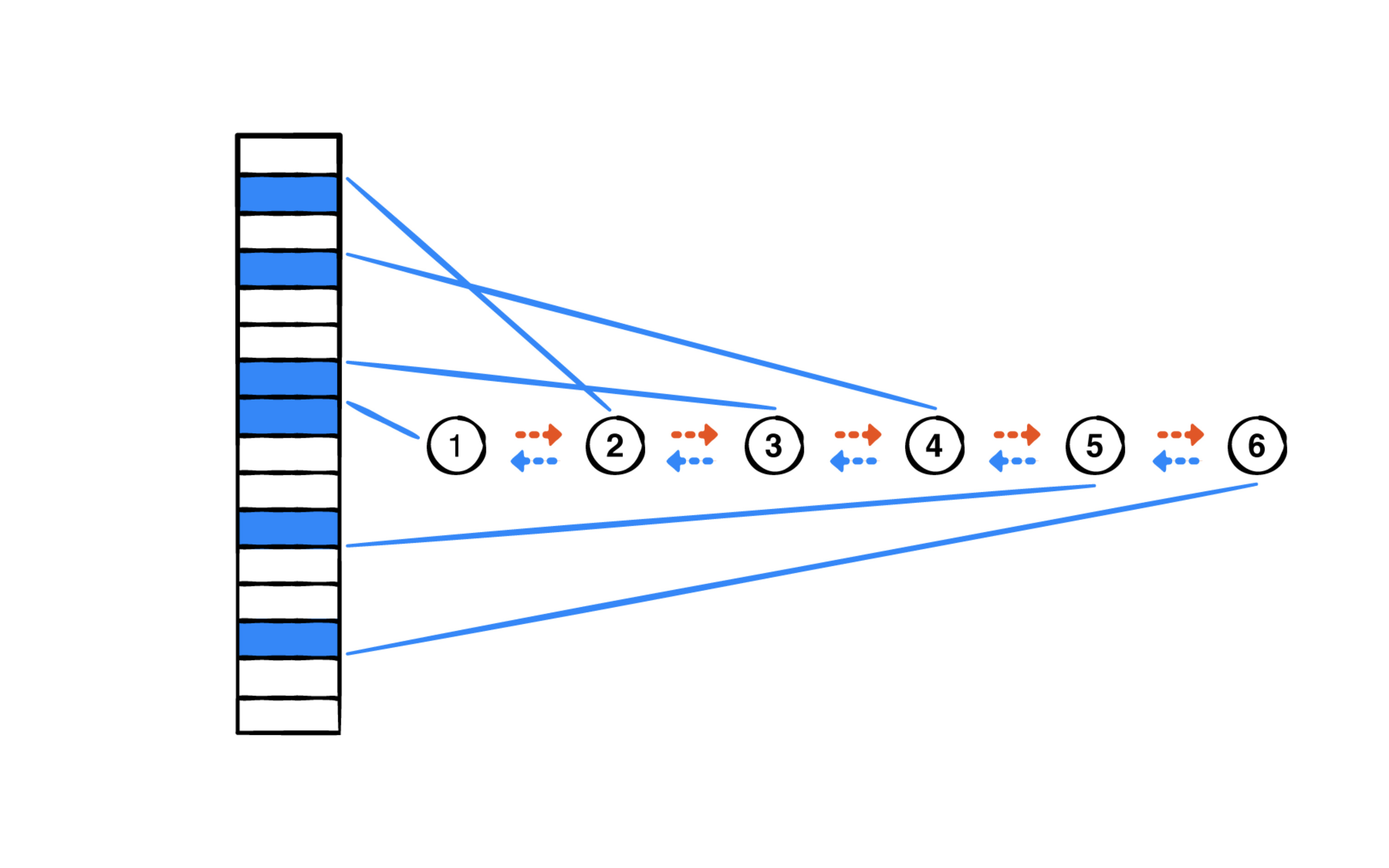
要点
队列数据结构是先进先出原则 (FIFO)，先添加到队列里面的元素先移除。
enqueue（入队）操作会插入一个元素到队列末尾。
dequeue（出队）操作会移除队列头部的元素。
数组里面的元素是连续分布的，而链表则是分散的，链表有可能丢失缓存数据。
如果队列的元素数目确定，那么使用环型缓冲区(Ring-Buffer)实现是很好的选择。
对比其它三种方式实现队列，使用栈队列的出队操作效率更加高效。
栈队列比链表队列在内存管理处更有优势。

试题
题目1：使用上面4种队列数据结构实现下面操作

默认数据：

执行下面操作：

enqueue("R")
enqueue("O")
dequeue()
enqueue("C")
dequeue()
dequeue()
enqueue("K")

环型缓冲区队列默认元素个数是5。

数组队列解决方案：

需要牢记的是，在数组的内存空间里，如果此时数组内存已满，那么再次添加一个元素进去，会导致数组内存直接加倍。

链表队列解决方案：

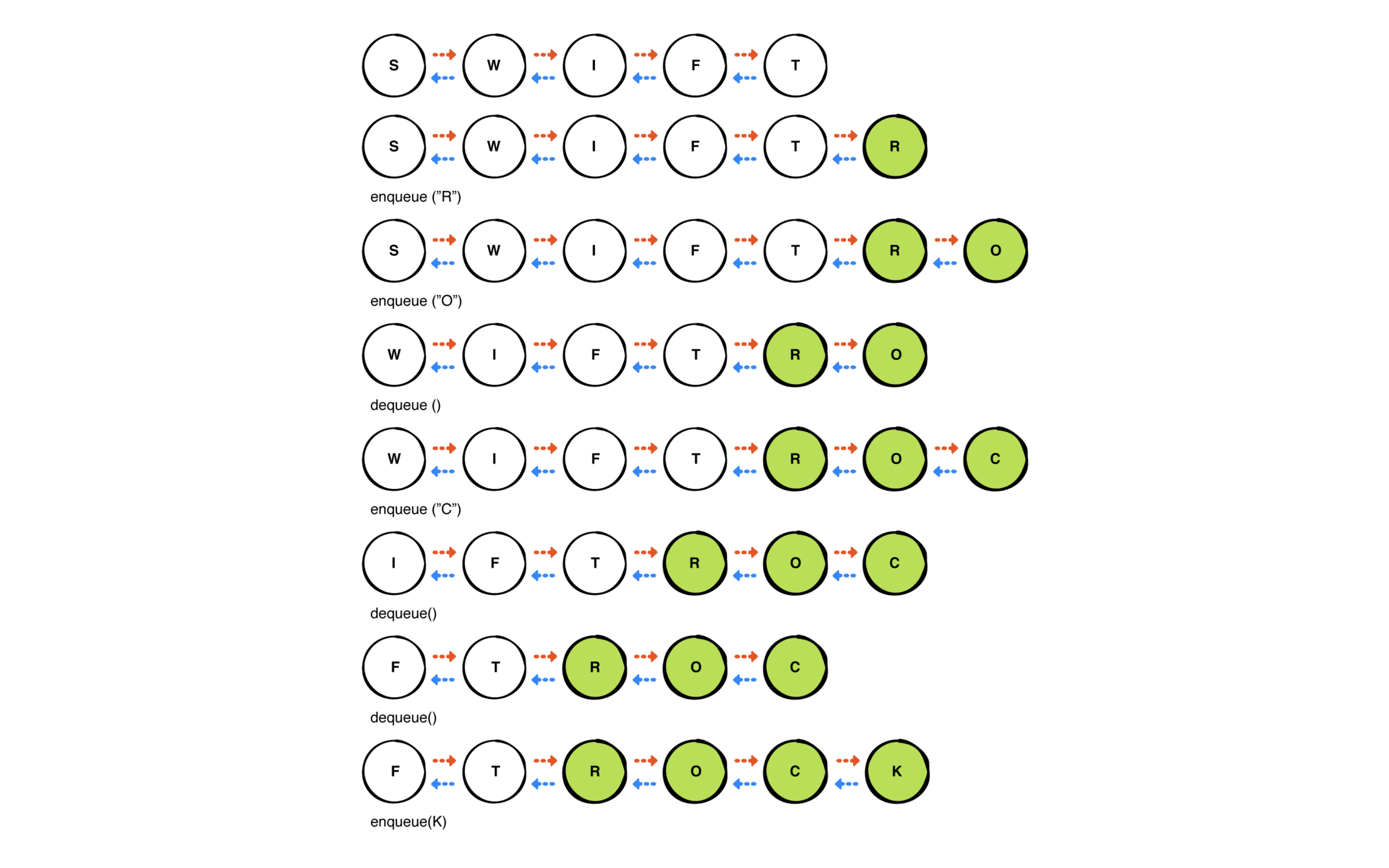
环型缓冲区队列解决方案：

这个需要记住的是由于里面的元素个数是固定的，入队操作可能失败。

栈队列解决方案：

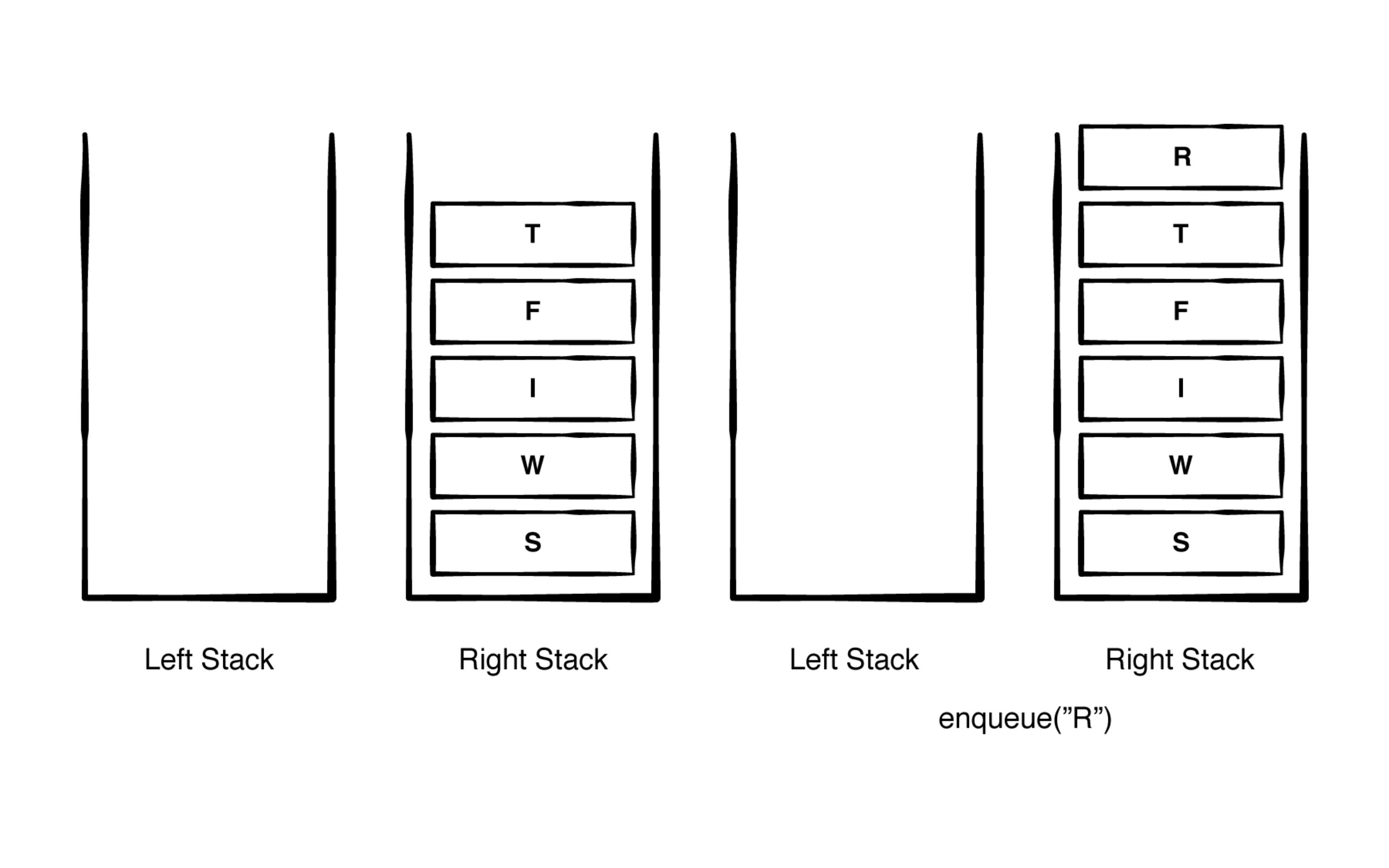
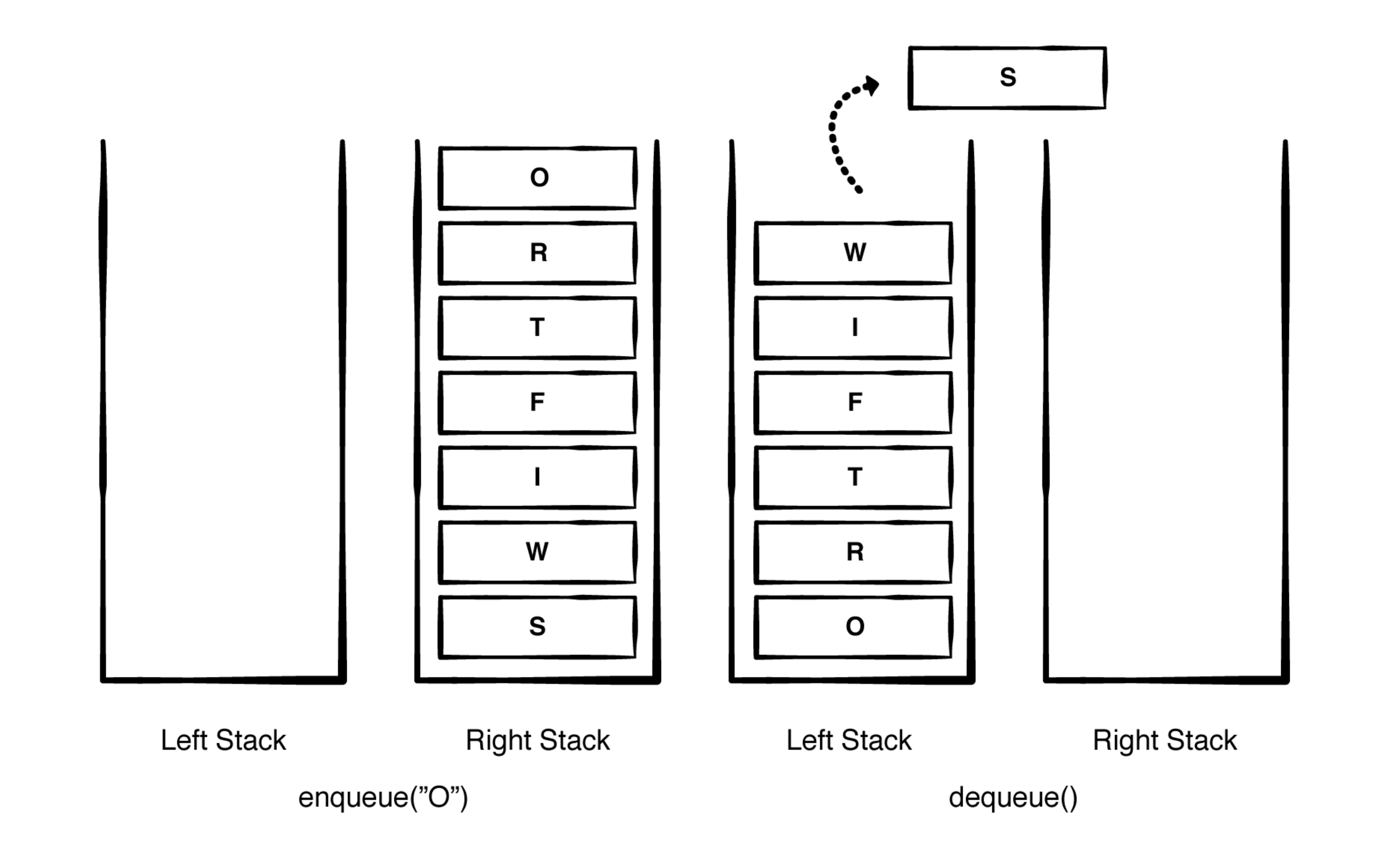
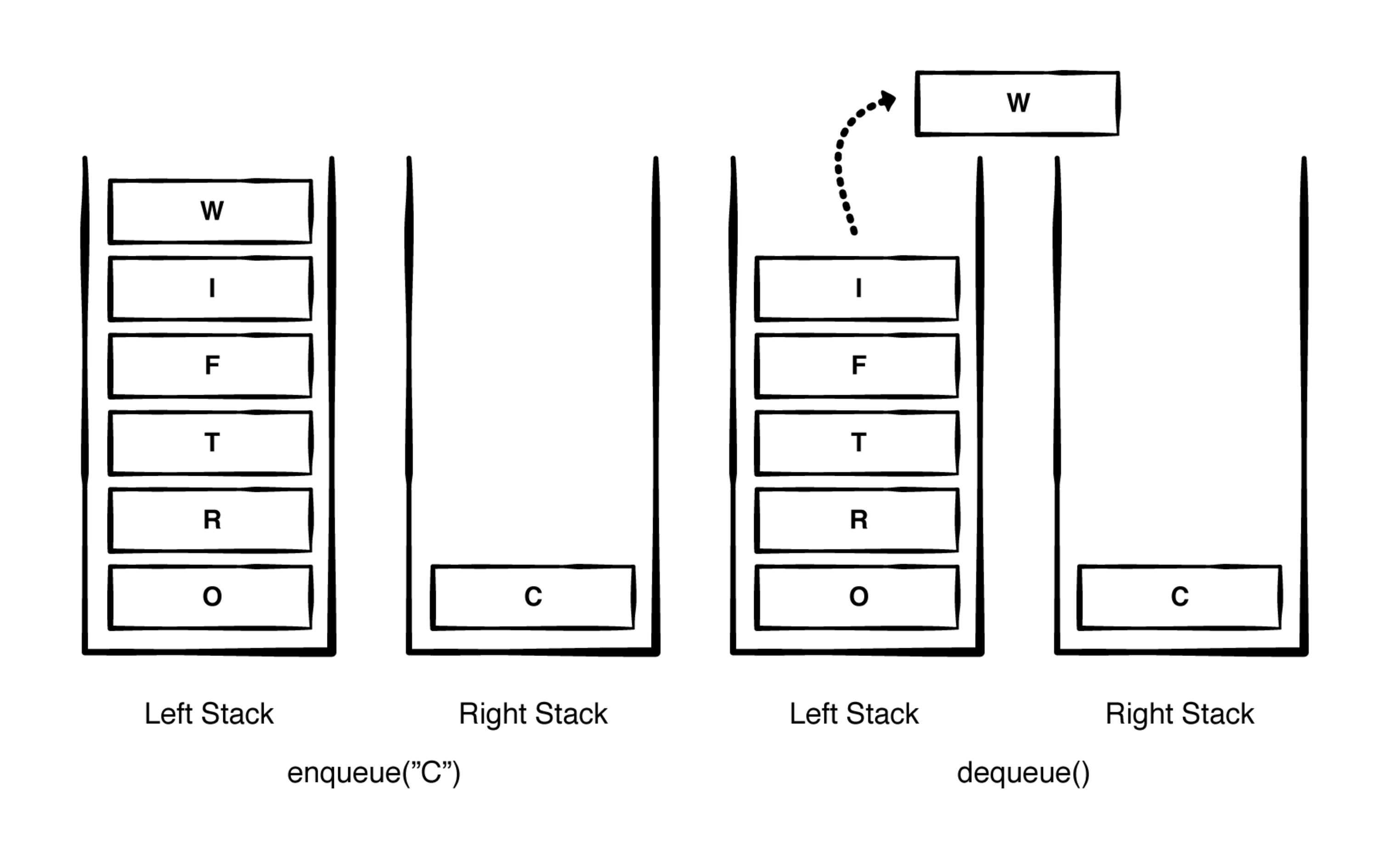
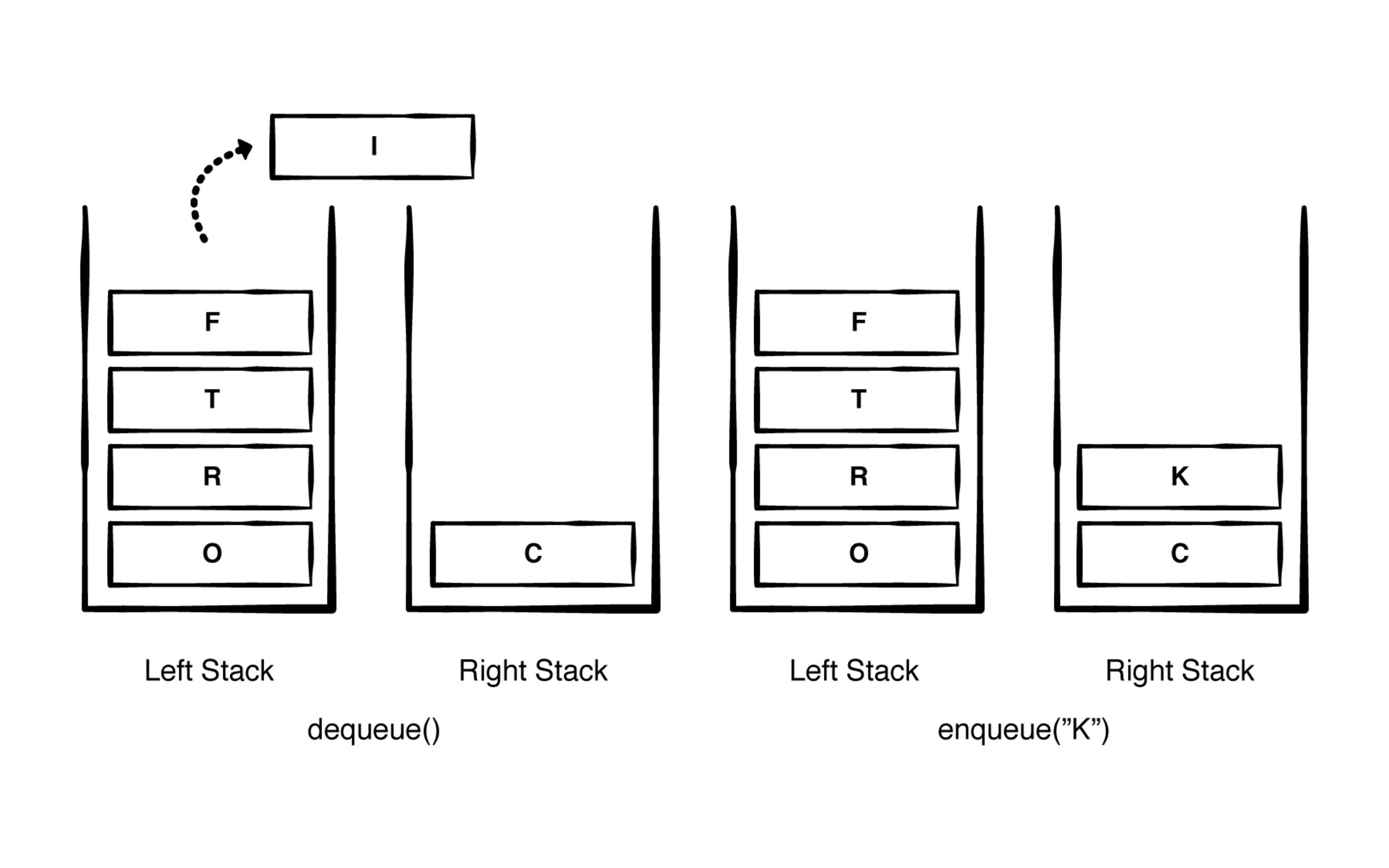
题目2：实现卡牌游戏中决定下一个出牌的人是谁

给出一个基本协议：

public protocol BoardGameManager {
    associatedtype Player
    mutating func nextPlayer() -> Player?
}

协议中有一个决定谁是下一个出牌人的方法。

下面使用数组队列实现：

extension QueueArray: BoardGameManager {
    
    public typealias Player = T
    
    public mutating func nextPlayer() -> Player? {
        // 决定出牌人出牌人
        guard let next = dequeue() else {
            return nil
        }
        // 把出队的人添加到队尾形成一个轮回
        enqueue(next)
        
        // 返回出牌人
        return next
    }
}

这个其实可以用之前实现的3种队列方式都实现一遍的😄。

测试：

var queue = QueueArray<String>()
queue.enqueue("Vincent")
queue.enqueue("Remel")
queue.enqueue("Lukiih")
queue.enqueue("Allison")
print(queue)

print("===== boardgame =======")
queue.nextPlayer()
print(queue)
queue.nextPlayer()
print(queue)
queue.nextPlayer()
print(queue)
queue.nextPlayer()
print(queue)

输出：

["Vincent", "Remel", "Lukiih", "Allison"]
===== boardgame =======
["Remel", "Lukiih", "Allison", "Vincent"]
["Lukiih", "Allison", "Vincent", "Remel"]
["Allison", "Vincent", "Remel", "Lukiih"]
["Vincent", "Remel", "Lukiih", "Allison"]

题目3：反转一个队列里面的元素

我们可以使用一个栈数据结构作为中转：

public struct Stack<Element> {
    
    private var storage: [Element] = []
    
    public init() { }
    
    public init(_ elements: [Element]) {
        storage = elements
    }
    
    public mutating func push(_ element: Element) {
        storage.append(element)
    }
    
    @discardableResult
    public mutating func pop() -> Element? {
        storage.popLast()
    }
    
    public func peek() -> Element? {
        storage.last
    }
    
    public var isEmpty: Bool {
        peek() == nil
    }
}

extension Stack: CustomStringConvertible {
    public var description: String {
        let topDivider = "----top----\n"
        let bottomDivider = "\n-----------"
        
        let stackElements = storage
            .map { "\($0)" }
            .reversed()
            .joined(separator: "\n")
        return topDivider + stackElements + bottomDivider
    }
}

extension Stack: ExpressibleByArrayLiteral {
    public init(arrayLiteral elements: Element...) {
        storage = elements
    }
}

栈的介绍可以看这里：基本数据结构 - Stack(栈)

下面是使用 数组队列 实现的：

extension QueueArray {
    
    mutating func reversed() -> QueueArray {
        var queue = self
        
        var stack = Stack<T>()
        
        while let next = queue.dequeue() {
            stack.push(next)
        }
        
        while let next = stack.pop() {
            queue.enqueue(next)
        }
        
        return queue
    }
}

测试：

var queue = QueueArray<String>()
queue.enqueue("1")
queue.enqueue("21")
queue.enqueue("18")
queue.enqueue("42")

print("before: \(queue)")
print("after: \(queue.reversed())")

输出：

before: ["1", "21", "18", "42"]
after: ["42", "18", "21", "1"]

题目4：实现一个头部和尾部都可以出队和入队的双端队列 Deque

下面是给出的基本信息。定义了一个方向的枚举 Direction。给了一个双端队列 Deque 的协议：

enum Direction {
    
    case front
    case back
}

protocol Deque {
    
    associatedtype Element
    var isEmpty: Bool { get }
    func peek(from direction: Direction) -> Element?
    mutating func enqueue(_ element: Element,
                          to direction: Direction) -> Bool
    mutating func dequeue(from direction: Direction) -> Element?
}

其实使用上面的4中队列形式都可以实现双端队列功能，这里选用的是双向链表实现。首先为之前的双向链表添加一个 last 属性，和 prepend 方法：

public class DoublyLinkedList<T> {
    
   // code code code .....
   // code code code .....
   // code code code .....

    
    public var last: Node<T>? {
        tail
    }
    
    public func prepend(_ value: T) {
        let newNode = Node(value: value)
        guard let headNode = head else {
            head = newNode
            tail = newNode
            return
        }
        
        newNode.previous = nil
        newNode.next = headNode
        headNode.previous = newNode
        
        head = newNode
    }
}

last：返回最后一个元素。

prepend：添加元素到头部。

实现：

class DequeDoublyList<T>: Deque {
    
    private var list = DoublyLinkedList<T>()
    
    typealias Element = T
    
    var isEmpty: Bool {
        return list.isEmpty
    }
    
    func peek(from direction: Direction) -> T? {
        switch direction {
        case .front:
            return list.first?.value
        case .back:
            return list.last?.value
        }
    }
    
    func enqueue(_ element: T, to direction: Direction) -> Bool {
        switch direction {
        case .front:
            list.prepend(element)
        case .back:
            list.append(element)
        }
        return true
    }
    
    func dequeue(from direction: Direction) -> T? {
        var element: T?
        switch direction {
        case .front:
            if let first = list.first {
                element = list.remove(first)
            }
        case .back:
            if let last = list.last {
                element = list.remove(last)
            }
        }
        return element
    }
    
}

其实代码的实现也很简单，就是使用一个双向链表作为底部的数据存储，然后对元素的操作判断方向即可。

基本数据结构 - Queue(队列)

基本操作

`数组队列`的实现

使用数组基本特性

enqueue（入队）

dequeue（出队）

Debug 和测试

优缺点分析

`链表队列`的实现

enqueue（入队）

dequeue（出队）

实现 peek 和 isEmpty

Debug 和测试

优缺点分析

`环型缓冲区队列`的实现

enqueue（入队）

dequeue（出队）

Debug 和测试

优缺点分析

`栈队列`的实现

使用数组特性

enqueue（入队）

dequeue（出队）

Debug 和测试

优缺点分析

要点

试题

题目1：使用上面4种队列数据结构实现下面操作

题目2：实现卡牌游戏中决定下一个出牌的人是谁

题目3：反转一个队列里面的元素

题目4：实现一个头部和尾部都可以出队和入队的双端队列 Deque

基本数据结构 - Queue(队列)

基本操作

数组队列的实现

使用数组基本特性

enqueue（入队）

dequeue（出队）

Debug 和测试

优缺点分析

链表队列的实现

enqueue（入队）

dequeue（出队）

实现 peek 和 isEmpty

Debug 和测试

优缺点分析

环型缓冲区队列的实现

enqueue（入队）

dequeue（出队）

Debug 和测试

优缺点分析

栈队列的实现

使用数组特性

enqueue（入队）

dequeue（出队）

Debug 和测试

优缺点分析

要点

试题

题目1：使用上面4种队列数据结构实现下面操作

题目2：实现卡牌游戏中决定下一个出牌的人是谁

题目3：反转一个队列里面的元素

题目4：实现一个头部和尾部都可以出队和入队的双端队列 Deque

`数组队列`的实现

`链表队列`的实现

`环型缓冲区队列`的实现

`栈队列`的实现