前言
-
文章首发于微信公众号【码猿技术专栏】
-
近期在做推荐系统中已读内容去重的相关内容,刚好用到了布隆过滤器,于是写了一篇文章记录分享一下。
-
文章的篇幅不是很长,主要讲了布隆过滤器的核心思想,目录如下: 
什么是布隆过滤器?
-
布隆过滤器是由一个长度为`m`比特的位**数组**与`k`个**哈希函数**组成的数据结构。比特数组均初始化为`0`,所有哈希函数都可以分别把输入数据尽量均匀地散列。
-
当**插入**一个元素时,将其数据通过`k`个哈希函数转换成`k`个哈希值,这`k`个哈希值将作为比特数组的`下标`,并将数组中的对应下标的值置为`1`。
-
当**查询**一个元素时,同样会将其数据通过`k`个哈希函数转换成`k`个哈希值(数组下标),查询数组中对应下标的值,如果有一个下标的值为`0`表明该元素一定不在集合中,如果全部下标的值都为`1`,表明该元素有`可能`在集合中。**至于为什么有可能在集合中?** 因为有可能某个或者多个下标的值为 1 是受到其他元素的影响,这就是所谓的`假阳性`,下文会详细讲述。
-
**无法删除一个元素**,为什么呢?因为你删除的元素的哈希值可能和集合中的某个元素的哈希值有相同的,一旦删除了这个元素会导致其他的元素也被删除。
-
下图示出一个`m=18`, `k=3`的布隆过滤器示例。集合中的 x、y、z 三个元素通过 3 个不同的哈希函数散列到位数组中。当查询元素 w 时,因为有一个比特为 0,因此 w 不在该集合中。 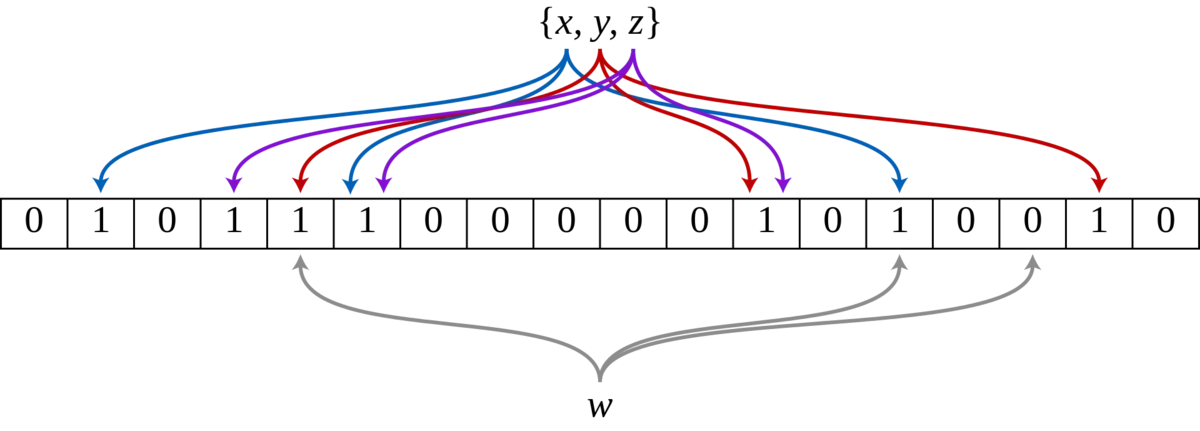
假阳性概率的计算
-
假阳性是布隆过滤器的一个痛点,因此需要不择一切手段来使假阳性的概率降低,此时就需要计算一下假阳性的概率了。
-
假设我们的哈希函数选择位数组中的比特时,都是等概率的。当然在设计哈希函数时,也应该尽量满足均匀分布。
-
在位数组长度`m`的布隆过滤器中插入一个元素,它的其中一个哈希函数会将某个特定的比特置为`1`。因此,在插入元素后,该比特仍然为 0 的概率是:
-
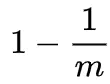
-
现有`k`个哈希函数,并插入`n`个元素,自然就可以得到该比特仍然为 0 的概率是: 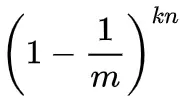
-
反过来讲,它已经被置为`1`的概率就是:
-
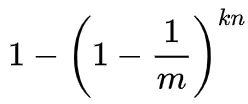
-
也就是说,如果在插入`n`个元素后,我们用一个不在集合中的元素来检测,那么被误报为存在于集合中的概率(也就是所有哈希函数对应的比特都为`1`的概率)为: 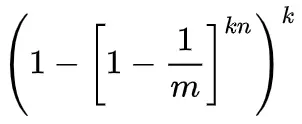
-
当`n`比较大时,根据极限公式,可以近似得出假阳性率:
-
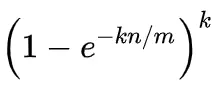
-
所以,在哈希函数个数`k`一定的情况下有如下结论:
-
位数组长度 m 越大,假阳性率越低。
-
已插入元素的个数 n 越大,假阳性率越高。
-
优点
-
用比特数组表示,不用存储数据本身,对空间的节省相比于传统方式占据绝对的优势。
-
时间效率很高,无论是插入还是查询,只需要简单的经过哈希函数转换,时间复杂度均为`O(k)`。
缺点
-
存在`假阳性`的概率,准确率要求高的场景不太适用。
-
只能插入和查询,不能删除了元素。
应用场景
-
布隆过滤器的用途很多,但是主要的作用就是去重,这里列举几个使用场景。
爬虫重复 URL 检测
-
试想一下,百度是一个爬虫,它会定时搜集各大网站的信息,文章,那么它是如何保证爬取到文章信息不重复,它会将 URL 存放到布隆过滤器中,每次爬取之前先从布隆过滤器中判断这个 URL 是否存在,这样就避免了重复爬取。当然这种存在假阳性的可能,但是只要你的比特数组足够大,`假阳性`的概率会很低,另一方面,你认为百度会在意这种的误差吗,你的一篇文章可能因为假阳性概率没有收录到,对百度有影响吗?
抖音推荐功能
-
读者朋友们应该没人没刷过抖音吧,每次刷的时候抖音给你的视频有重复的吗?他是如何保证推荐的内容不重复的呢?
-
最容易想到的就是抖音会记录用户的历史观看记录,然后从历史记录中排除。这是一种解决办法,但是性能呢?不用多说了,有点常识的都知道这不可能。
-
解决这种重复的问题,布隆过滤器有着绝对的优势,能够很轻松的解决。
防止缓存穿透
-
缓存穿透是指查询一条数据库和缓存都没有的一条数据,就会一直查询数据库,对数据库的访问压力会一直增大。
-
布隆过滤器在解决缓存穿透的问题效果也是很好,这里不再细说,后续文章会写。
如何实现布隆过滤器?
-
了解布隆过滤器的设计思想之后,想要实现一个布隆过滤器其实很简单,陈某这里就不再搬门弄斧了,介绍一下现成的实现方式吧。
Redis 实现
-
Redis4.0 之后推出了插件的功能,下面用 docker 安装:
docker pull redislabs/rebloom docker run -p6379:6379 redislabs/rebloom
-
安装完成后连接 redis 即可,运行命令:
redis-cli
-
至于具体的使用这里不再演示了,直接看官方文档和教程,使用起来还是很简单的。
Guava 实现
-
guava 对应布隆过滤器的实现做出了支持,使用 guava 可以很轻松的实现一个布隆过滤器。
1. 创建布隆过滤器
-
创建布隆过滤器,如下:
BloomFilter filter = BloomFilter.create( Funnels.integerFunnel(), 5000, 0.01); //插入 IntStream.range(0, 100_000).forEach(filter::put); //判断是否存在 boolean b = filter.mightContain(1);
-
`arg1`:用于将任意类型 T 的输入数据转化为 Java 基本类型的数据,这里转换为 byte
-
`arg2`:byte 字节数组的基数
-
`arg3`:期望的假阳性概率
2.估计最优 m 值和 k 值
-
guava 在底层对 byte 数组的基数(m)和哈希函数的个数 k 做了自己的算法,源码如下:
//m值的计算 static long optimalNumOfBits(long n, double p) { if (p == 0) { p = Double.MIN_VALUE; } return (long) (-n * Math.log(p) / (Math.log(2) * Math.log(2))); }
//k值的计算 static int optimalNumOfHashFunctions(long n, long m) { // (m / n) * log(2), but avoid truncation due to division! return Math.max(1, (int) Math.round((double) m / n * Math.log(2))); }
-
想要理解 guava 的计算原理,还要从的上面推导的过程继续。
-
由假阳性率的近似计算方法可知,如果要使假阳性率尽量小,在 m 和 n 给定的情况下,`k`值应为:
-
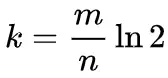
-
将 k 代入上一节的式子并化简,我们可以整理出期望假阳性率 p 与 m、n 的关系: 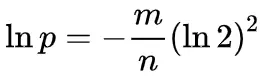
-
换算而得:
-
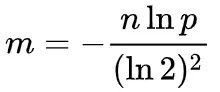
-
根据以上分析得出以下的结论:
-
如果指定期望假阳性率 p,那么最优的 m 值与期望元素数 n 呈线性关系。
-
最优的 k 值实际上只与 p 有关,与 m 和 n 都无关,即: 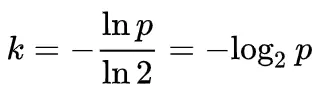
-
综上两个结论,在创建布隆过滤器的时候,确定`p`值和`m`值很重要。
-
总结
-
至此,布隆过滤器的知识介绍到这里,如果觉得陈某写得不错的,转发在看点一波,读者的一份支持将会是我莫大的鼓励。
-
**另外想和陈某私聊或者想要加交流群的朋友,公众号回复关键词`加群`加陈某微信,陈某会第一时间拉你进群。**
巨人的肩膀
-
https://blog.csdn.net/u012422440/article/details/94088166
-
https://blog.csdn.net/Revivedsun/article/details/94992323