1.二进制中1的个数

class Solution {
public:
int NumberOf1(int n) {
int num = 0;
while (n != 0) {
num++;
n &= (n - 1);
}
return num;
}
};
2.数值的整数次方

链接:https://www.nowcoder.com/questionTerminal/1a834e5e3e1a4b7ba251417554e07c00?answerType=1&f=discussion
来源:牛客网
public class Solution {
public double Power(double base, int exponent) {
if (base == 0.0){
return 0.0;
}
// 前置结果设为1.0,即当exponent=0 的时候,就是这个结果
double result = 1.0d;
// 获取指数的绝对值
int e = exponent > 0 ? exponent : -exponent;
// 根据指数大小,循环累乘
for(int i = 1 ; i <= e; i ++){
result *= base;
}
// 根据指数正负,返回结果
return exponent > 0 ? result : 1 / result;
}
}
3.整数中1出现的次数

思路是分别计算个位、十位、百位........上出现 1 的个数。 以 n =216为例: 个位上: 1 ,11,21,31,.....211。个位上共出现(216/10)+ 1个 1 。因为除法取整,210~216间个位上的1取不到,所以我们加8进位。你可能说为什么不加9,n=211怎么办,这里把最后取到的个位数为1的单独考虑,先往下看。 十位上:10~19,110~119,210~216. 十位上可看成 求(216/10)=21 个位上的1的个数然后乘10。这里再次把最后取到的十位数为1的单独拿出来,即210~216要单独考虑 ,个数为(216%10)+1 .这里加8就避免了判断的过程。 后面以此类推。 时间复杂度 O(logN)
链接:https://www.nowcoder.com/questionTerminal/bd7f978302044eee894445e244c7eee6?answerType=1&f=discussion
来源:牛客网
ublic int NumberOf1Between1AndN_Solution(int n) {
int cnt = 0;
for (int m = 1; m <= n; m *= 10) {
int a = n / m, b = n % m;
cnt += (a + 8) / 10 * m + (a % 10 == 1 ? b + 1 : 0);
}
return cnt;
}
4.丑数

链接:https://www.nowcoder.com/questionTerminal/6aa9e04fc3794f68acf8778237ba065b?answerType=1&f=discussion
来源:牛客网
public class Solution {
public int GetUglyNumber_Solution(int index) {
if(index <= 0)return 0;
int p2=0,p3=0,p5=0;//初始化三个指向三个潜在成为最小丑数的位置
int[] result = new int[index];
result[0] = 1;//
for(int i=1; i < index; i++){
result[i] = Math.min(result[p2]*2, Math.min(result[p3]*3, result[p5]*5));
if(result[i] == result[p2]*2)p2++;//为了防止重复需要三个if都能够走到
if(result[i] == result[p3]*3)p3++;//为了防止重复需要三个if都能够走到
if(result[i] == result[p5]*5)p5++;//为了防止重复需要三个if都能够走到
}
return result[index-1];
}
}
5.扑克牌顺子

链接:https://www.nowcoder.com/questionTerminal/762836f4d43d43ca9deb273b3de8e1f4?answerType=1&f=discussion
来源:牛客网
import java.util.TreeSet;
public class Solution {
public boolean isContinuous(int [] n) {
if (n.length < 5 || n.length > 5) {
return false;
}
int num = 0;
TreeSet<Integer> set = new TreeSet<> ();
for (int i=0; i<n.length;i++) {
if (n[i]==0) {
num ++;
} else {
set.add(n[i]);
}
}
if ((num + set.size()) != 5) {
return false;
}
if ((set.last() - set.first()) < 5) {
return true;
}
return false;
}
}
6.孩子们的游戏

public class Solution {
public int LastRemaining_Solution(int n, int m) {
//递归+模拟
if(n==0)return -1;
if(n==1)return 0;
return (LastRemaining_Solution(n-1,m)+m)%n;
}
}
7.求1+2+3+...+n

public class Solution {
public int Sum_Solution(int n) {
//短路求值定理 记录blog!
int sum=n;
boolean flag=(sum>0)&&((sum+=Sum_Solution(n-1))>0);
return sum;
}
}
8.不用加减乘除做加法

public class Solution {
public int Add(int num1,int num2) {
//两个数异或:相当于每一位相加,而不考虑进位;
//两个数相与,并左移一位:相当于求得进位;
//将上述两步的结果相加
while( num2!=0 ){
int sum = num1 ^ num2;
int carray = (num1 & num2) << 1;
num1 = sum;
num2 = carray;
}
return num1;
}
}
9.和为S的连续正数序列
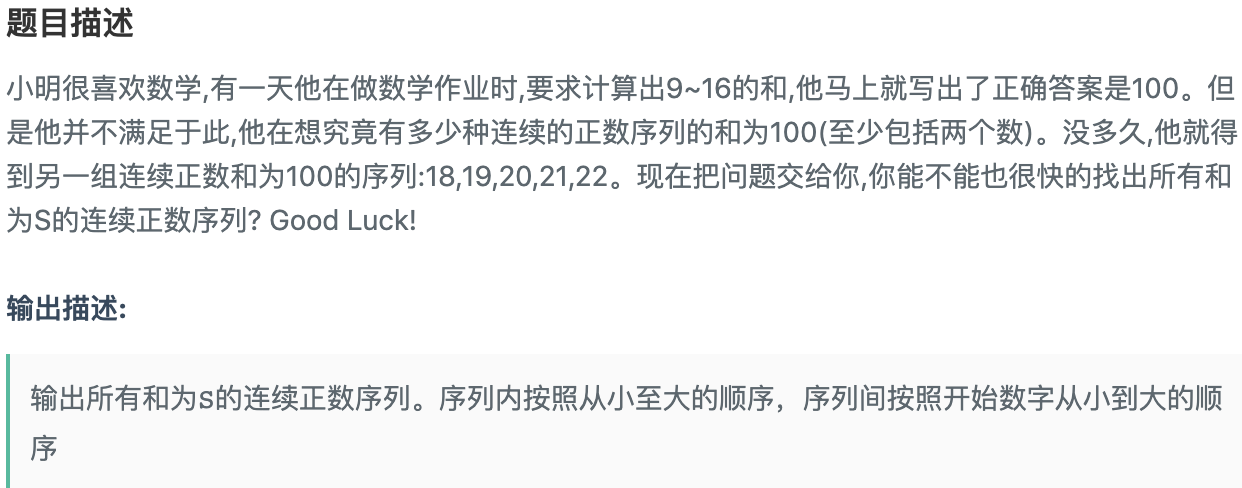
import java.util.ArrayList;
public class Solution {
public ArrayList<ArrayList<Integer> > FindContinuousSequence(int sum) {
//双指针技术
//用一个数组记录结果
ArrayList<ArrayList<Integer> > result=new ArrayList<>();
//标记两个指针
int a=1,b=2;
//用循环判断
//结束标志是当左指针a超过右指针b
while(a<b){
int s=(a+b)*(b-a+1)/2;
if(s==sum){
ArrayList<Integer >list=new ArrayList<>();
for(int i=a;i<=b;i++){
list.add(i);
}
result.add(list);
}else if(s<sum){
b++;
}else{
a++;
}
}
return result;
}
}
10.和为S的两个数

import java.util.ArrayList;
public class Solution {
public ArrayList<Integer> FindNumbersWithSum(int [] array,int sum) {
//跟上题一模一样
//因为外圈乘积最小,记住啦!
ArrayList<Integer> result=new ArrayList<Integer>();
if(array.length<=1||array==null)return result;
int smallindex=0;
int bigindex=array.length-1;
while(smallindex<bigindex){
int s=array[bigindex]+array[smallindex];
if(s==sum){
result.add(array[smallindex]);
result.add(array[bigindex]);
break;
}else if(s<sum){
smallindex++;
}else{
bigindex--;
}
}
return result;
}
}
11.最小的K个数

12.数据流中的中位数
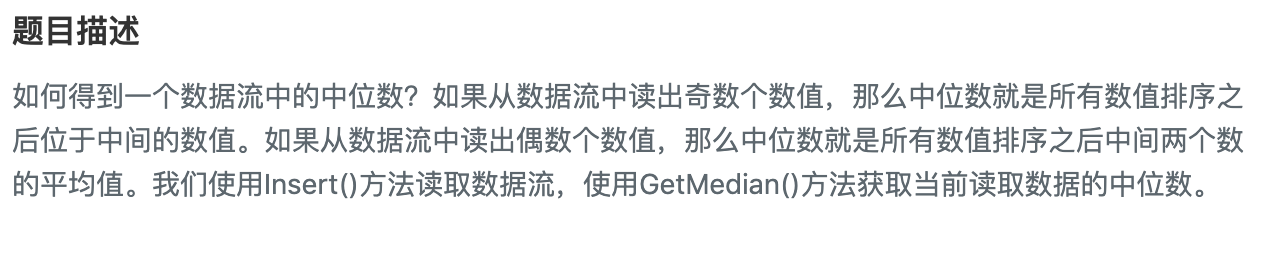
13.滑动窗口最大值

14.矩阵中的路径
dfs

15.机器人的活动范围
