01 逐步求和得到正数的最小值
题目描述【Easy】
给你一个整数数组 nums 。你可以选定任意的 正数 startValue 作为初始值。
你需要从左到右遍历 nums 数组,并将 startValue 依次累加上 nums 数组中的值。
请你在确保累加和始终大于等于 1 的前提下,选出一个最小的 正数 作为 startValue 。
示例: 输入:nums = [-3,2,-3,4,2] 输出:5 解释:如果你选择 startValue = 4,在第三次累加时,和小于 1 。 累加求和 startValue = 4 | startValue = 5 | nums (4 -3 ) = 1 | (5 -3 ) = 2 | -3 (1 +2 ) = 3 | (2 +2 ) = 4 | 2 (3 -3 ) = 0 | (4 -3 ) = 1 | -3 (0 +4 ) = 4 | (1 +4 ) = 5 | 4 (4 +2 ) = 6 | (5 +2 ) = 7 | 2
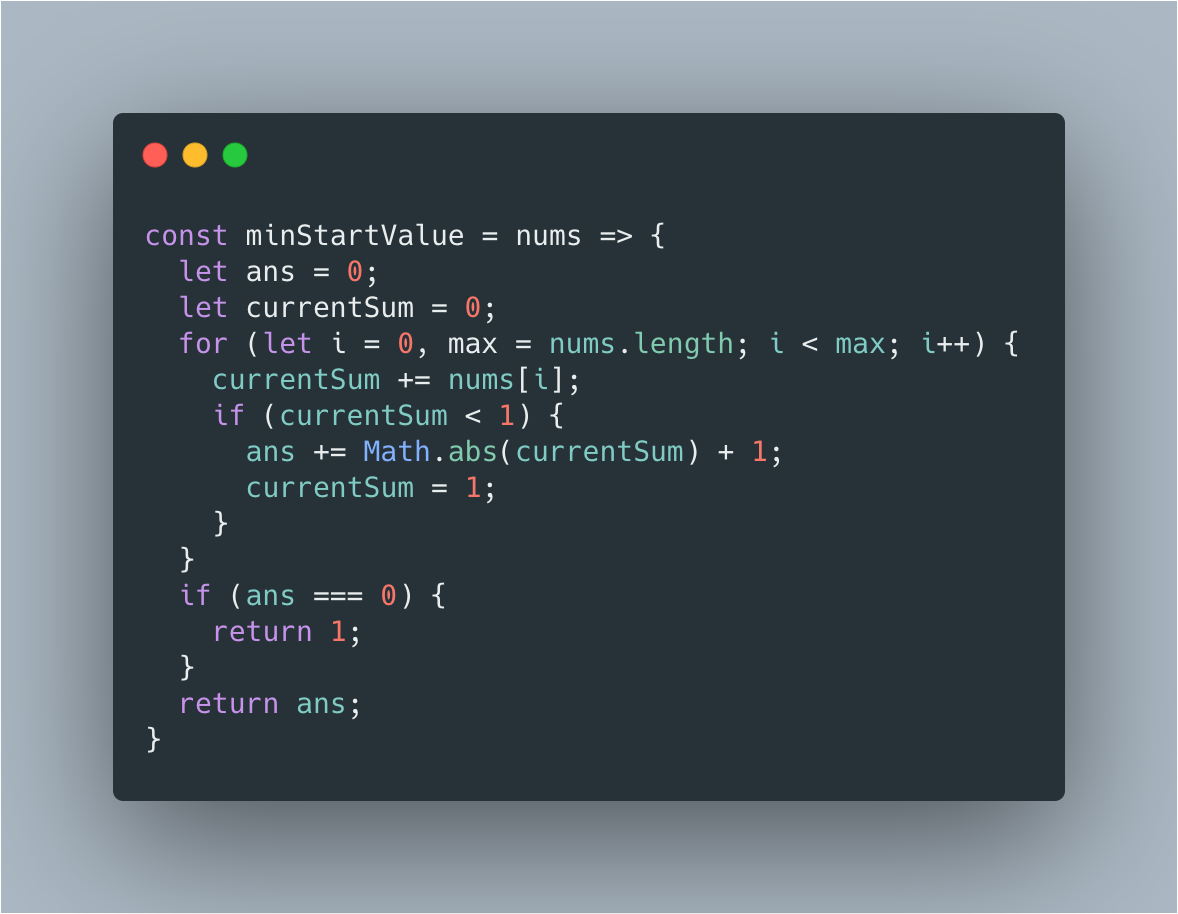
解决本题需要把握以下两个条件:
累加过程中确保当前值大于等于 1
最终结果应该是一个正整数
时间复杂度 O(n),空间复杂度 O(1)。
02 和为K的最少斐波那契数字数目
题目描述【Medium】
给你数字 k ,请你返回和为 k 的斐波那契数字的最少数目,其中,每个斐波那契数字都可以被使用多次。 斐波那契数字定义为:
F1 = 1 F2 = 1 Fn = Fn-1 + Fn-2 , 其中 n > 2 。 数据保证对于给定的 k ,一定能找到可行解。
示例: 输入:k = 7 输出:2 解释:斐波那契数字为:1,1,2,3,5,8,13 对于 k = 7,可以得到 2 + 5 = 7
第一步:计算出不大于 k 值的斐波那契数列。
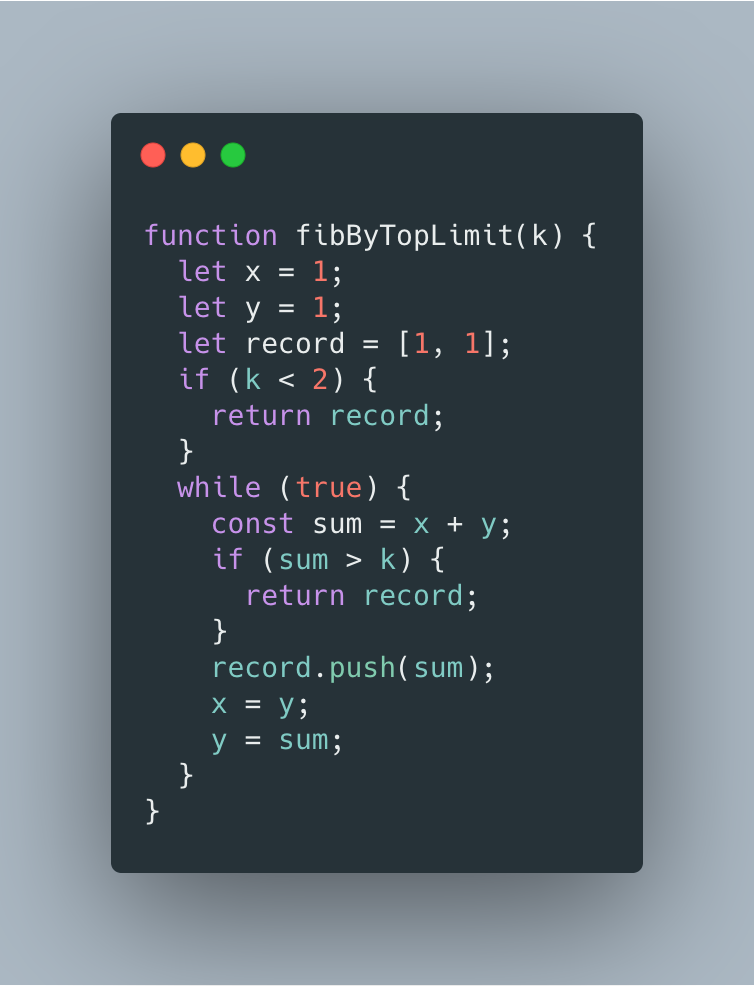
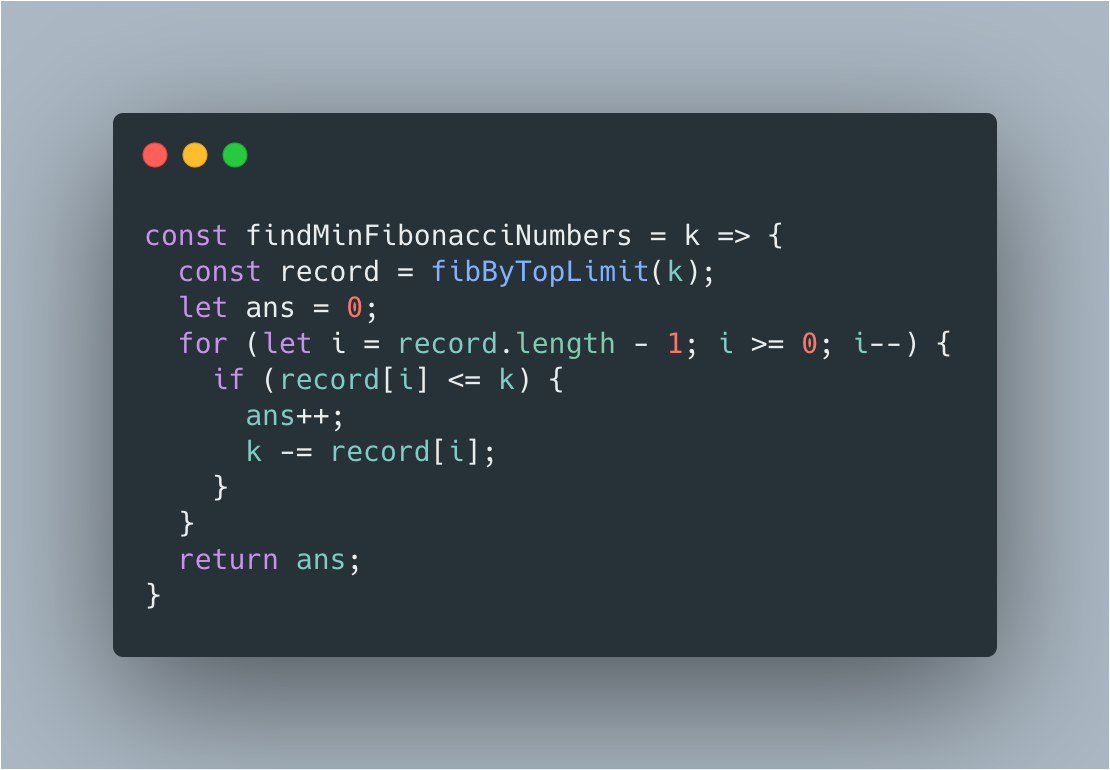
第二步:利用贪心策略,优先选择最大的斐波那契数。
时间复杂度 O(n),空间复杂度 O(n)。
03 长度为n的开心字符串
题目描述【Medium】
一个 「开心字符串」定义为:
仅包含小写字母 ['a', 'b', 'c']. 对所有在 1 到 s.length - 1 之间的 i ,满足 s[i] != s[i + 1] (字符串的下标从 1 开始)。 比方说,字符串 'abc','ac','b' 和 'abcbabcbcb' 都是开心字符串,但是 'aa','baa' 和 'ababbc' 都不是开心字符串。
给你两个整数 n 和 k ,你需要将长度为 n 的所有开心字符串按字典序排序。
请你返回排序后的第 k 个开心字符串,如果长度为 n 的开心字符串少于 k 个,那么请你返回 空字符串 。
示例: 输入:n = 1, k = 3 输出:'c' 解释:列表 ['a', 'b', 'c'] 包含了所有长度为 1 的开心字符串。按照字典序排序后第三个字符串为 'c' 。
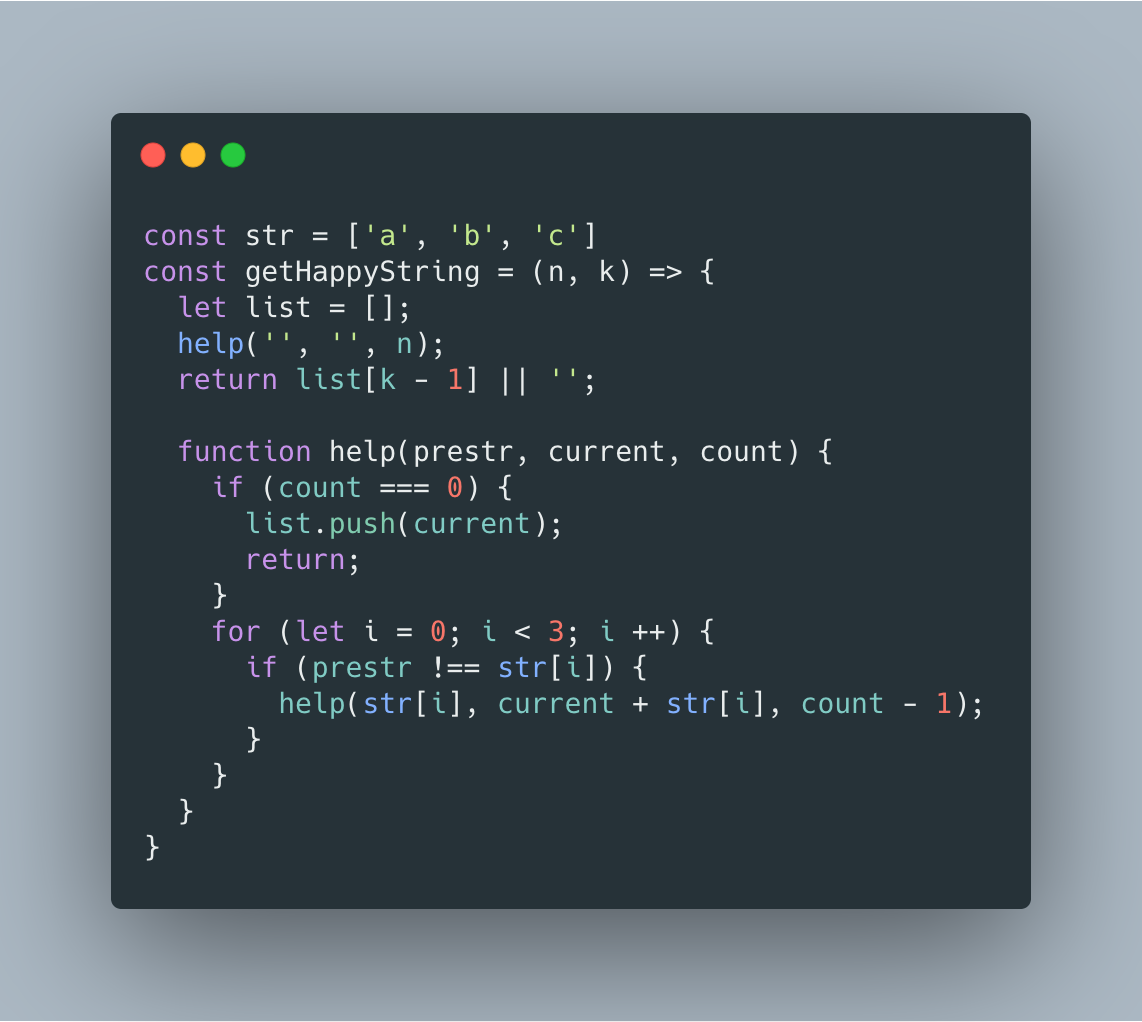
本道题中 n 的范围是 [1, 10],所以完全可以按照字典序 BFS 出所有情况。
时间复杂度 O(2^n),空间复杂度 O(n)。
04 恢复数组
题目描述【Hard】
某个程序本来应该输出一个整数数组。但是这个程序忘记输出空格了以致输出了一个数字字符串,我们所知道的信息只有:数组中所有整数都在 [1, k] 之间,且数组中的数字都没有前导 0 。
给你字符串 s 和整数 k 。可能会有多种不同的数组恢复结果。
按照上述程序,请你返回所有可能输出字符串 s 的数组方案数。
由于数组方案数可能会很大,请你返回它对 10^9 + 7 取余 后的结果。
示例: 输入:s = '1000',k = 10000 输出:1 解释:唯一可能的方案数 [1000]
本道题采用动态规划求解。
定义状态:dp[i] 表示从 i 到 n(字符串末尾)可以输出的方案数。
状态转移方程:dp[i] = dp[i + 1] + dp[i + 2] ... + dp[i + j] (i + j <= n)。
对于任意 dp[i + j] 需要满足以下两个条件:
s[i] 不为 0
Number.parseInt(s[i, j]) 不大于 k
时间复杂度 O(n^2),空间复杂度 O(n)。

05 往期精彩回顾
