1、关于递归

• 特点：
  • 函数会不停调用自己，每次调用的参数略有不同
  • 当满足某个简单条件时，则实现一个简单的调用
  • 最终算出结果
• 理解：
  • 可以用代入法快速理解递归
  • 可以用调用栈快速理解

2、选择排序

把一个数组从小到大进行排列

• 第一次从待排序的数组中选出最小的一个元素，放在第一位，然后再从剩余的未排序元素中寻找到最小的元素，然后放到已排序的数组的最后。 以此类推，直到全部待排序的数据元素的个数为零。

let minIndex = (numbers) =>{
    let index = 0
    for(let i = 1;i<numbers.length;i++){
        if(numbers[i]<numbers[index]){
            index = i
        }
    }
    return index
}

let swap = (numbers,i,j) => {
    let temp = numbers[i]
    numbers[i] = numbers[j]
    numbers[j] = temp
}

let sort = (numbers) => {
    for(let i=0;i<numbers.length-1;i++){
        let index = minIndex(numbers.slice(i))+i
        swap(numbers,index,i)
    }
    return numbers
}

sort([5,3,1,6,4])  //[1, 3, 4, 5, 6]

3、快速排序

let sort = (numbers) => {
    if(numbers.length <=1){return numbers}
    let sortIndex = Math.floor(numbers.length/2)
    let sortNumber = numbers.splice(sortIndex,1)[0]
    let left = []
    let right = []
    for(let i=0;i<numbers.length;i++){
        if(numbers[i]<sortNumber){
            left.push(numbers[i])
        }else{
            right.push(numbers[i])
        }
    }
    return sort(left).concat([sortNumber],sort(right))
}

sort([34,2,4,74,3,1])  //[1, 2, 3, 4, 34, 74]

• 图解：

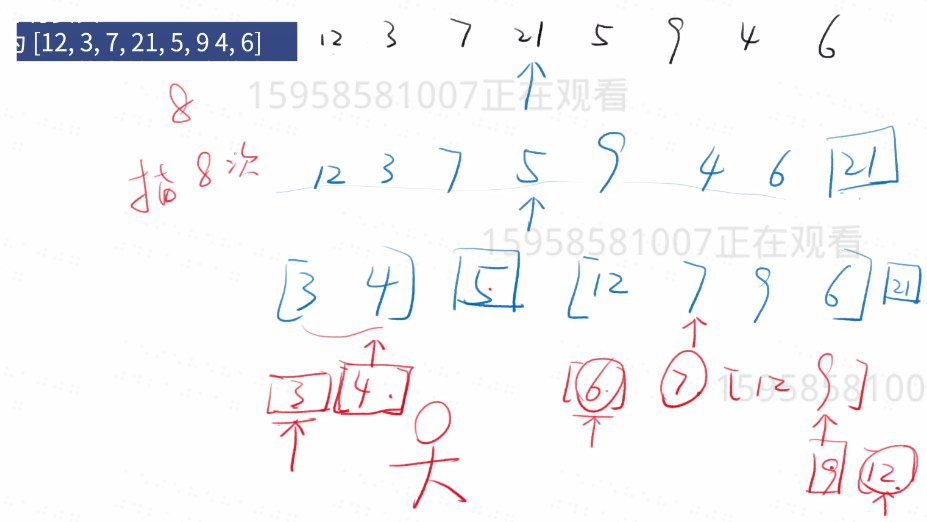
4、归并排序

let mergeSort = (numbers) => {
    if(numbers.length ===1){return numbers}
    let left = numbers.slice(0,Math.floor(numbers.length/2))
    let right = numbers.slice(Math.floor(numbers.length/2))
    console.log('left:' +left)
    console.log('right:' +right)
    return merge(mergeSort(left),mergeSort(right))
}
let merge = (a,b) =>{
    if(a.length === 0){return b}
    if(b.length === 0){return a}
    if(a[0]<b[0]){
        return [a[0]].concat(merge(a.slice(1),b))
    }else{
        return [b[0]].concat(merge(a,b.slice(1)))
    }
}

mergeSort([4,2,14,11,7,1])    // [1, 2, 4, 7, 11, 14]

• 图解：

  

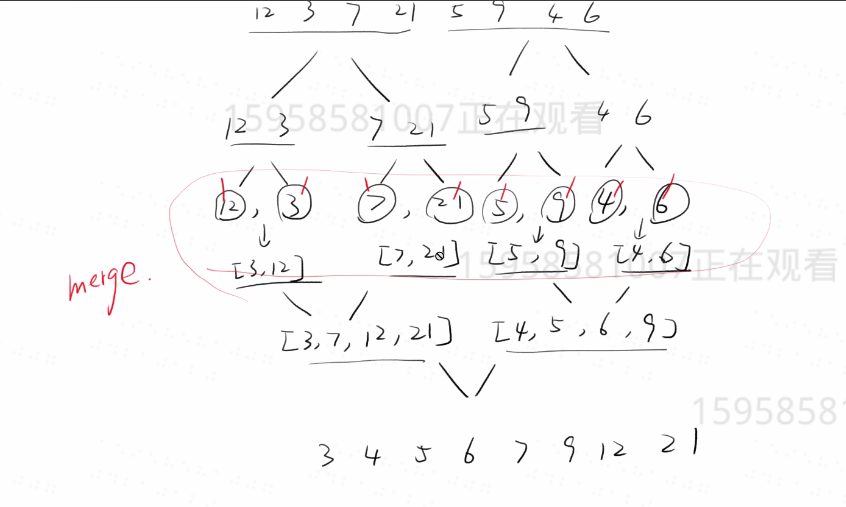
5、计数排序

let countSort = (arr) =>{
    let hashTable = {}
    let max = 0
    let result = []
    for(let i=0;i<arr.length;i++){
        if(!(arr[i] in hashTable)){
            hashTable[arr[i]] = 1
        }else{
            hashTable[arr[i]] +=1
        }
        if (arr[i]>max){
            max = arr[i]
        }
    }
    
    for(let j=0;j<=max;j++){
        if(j in hashTable){
            for(let z=0;z < hashTable[j];z++){
                result.push(j)
            }
        }
    }
    return result
}

countSort([4,12,11,9,3,2,1,1,1])  //[1,1,1,2,3,4,9,11,12]

• 图解：

  

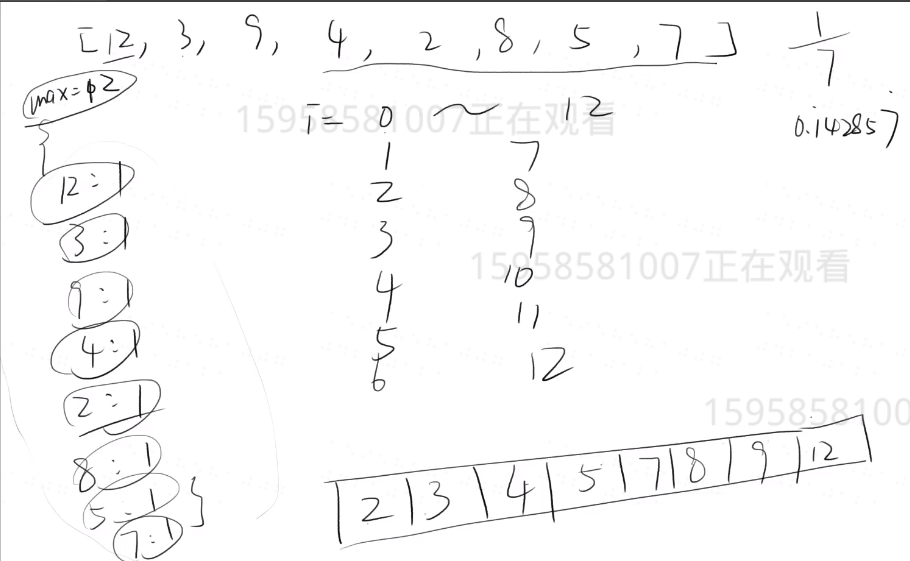
6、时间复杂度对比

• 选择排序（n^2）
• 快速排序（n* log2n）
• 归并排序（n* log2n）
• 计数排序（n+(max-min)）

声明：本文内容为饥人谷与本人所共同拥有，转载请注明出处