描述

给定一个原字符串(string)和模式串(pattern)，要求打印出模式串在原字符串中出现的位置。

实例

输入:  string = "abdadc"  pattern = "ad"
输出:  3

思路1-BF（Brute Force，暴力检索)

暴力法是很容易就能想到的思路

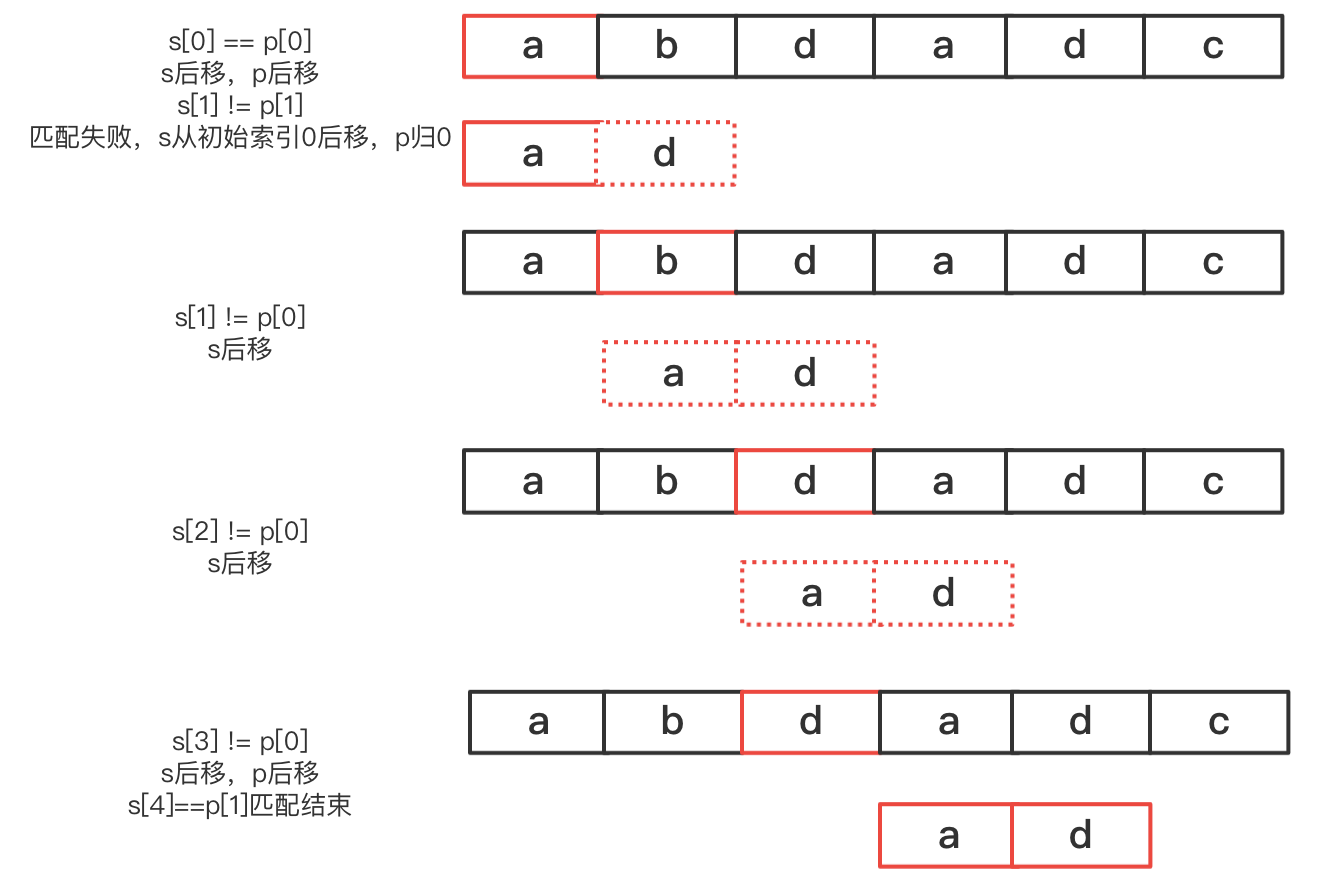
从i=0开始，依次对比s[i]和p[0]的值
如果s[i]==p[i]，对比s[i+1]和p[1]的值，直到s[i+n-1]== p[n-1]，说明字符串匹配成功。打印出当前i即可。
否则i=i+1，从步骤1重新开始对比。

void BF(char* s, char* p) {
    bool findFlag = false;
    //如果i到原字符串s末尾的距离小于p的长度，则不用计算，因为此时p已经不可能匹配成功
    for(int i = 0; i <= (strlen(s) - strlen(p)); i++) {
        int indexP = 0;
        int j = i;
        while(indexP < strlen(p)) {
            if(s[j] == p[indexP]) {
                j++;
                indexP++;
                if(indexP == strlen(p)) {
                    findFlag = true;
                    printf("匹配成功，位置为%d\n", i);
                }
            }else {
                break;
            }
        }
    }
    if(!findFlag) {
        printf("匹配失败\n");
    }
}

时间复杂度为o(n*m)，其中n为原字符串s的长度，m为模式串p的长度。

思路2-RK算法

RK算法全程Rabin-Karp，是根据算法发明者的名字来命名的。

在BF算法中，简单粗暴地对两个字符串中的所有字符依次进行比较，那么有没有简单的方法可以一次得出两个字符串对比的值呢？这就是RK算法和BF算法中不一样的地方了。PK算法比较的是两个字符串的hash值。

计算字符串hash值的算法有很多，拿最简单的按位相加来距离，把abcd...z看作是123456...24，把字符串的所有字符串对应的值相加，得出的结果就是hashcode。

例如：
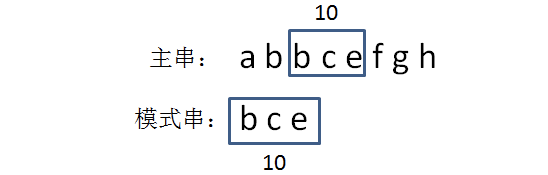
字符串"bce"的hashcode为：2+3+5=10

需要注意的是，不同的hash算法产生hash冲突的概率也不一样，按位相加产生hash冲突的概率就比较大，只是拿来举例说明，由于hash冲突的存在，当我们匹配到两个hashcode一样的字符串时，还需要通过BF来对当前子串和模式串进行验证，确保完全匹配。

生成模式串的hashcode

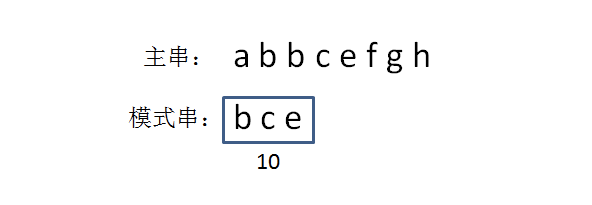
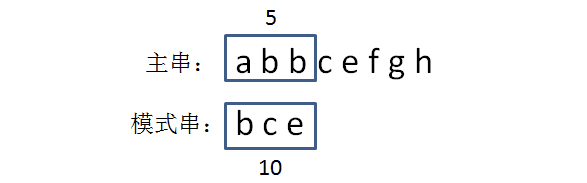
2. 生成主串当中第一个等长子串的hashcode，与模式串进行比较

发现不匹配，继续下一轮比较

生成主串当中第二个等长子串的hashcode，与模式串进行比较

5. 依次类推，找到如下子串

6. 此时，虽然子串和模式串hashcode相等，但是由于hash冲突的存在，需要利用BF法对子串和模式串进行验证，最终验证成功，匹配完成。

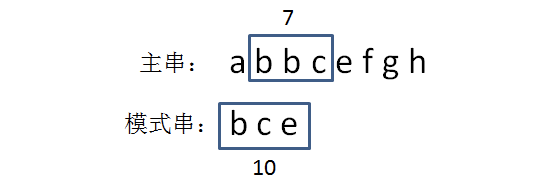
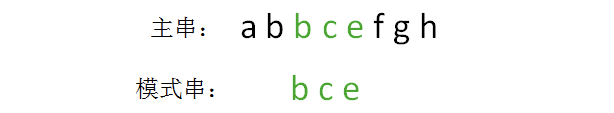
hash算法的优化

当前使用的hash算法为按位相加的算法，如果每一次改变主串的子串都重新计算hashcode的话，显然时间复杂度为o(m)，遍历n次之后，时间复杂度为o(m*n)。可以通过改进，使hash算法的时间复杂度降低。

实例中两个相邻子串abb和bbc除了abb的首字符a和bbc的尾字符c外，其他的字符都相同，我们可以根据这一点对hash算法进行优化。

old     new
abb     bbc

newHash = oldHash - 1 + 3

其中old的首字符a对应的hash为1，new的尾字符c对应的hash为3。
通过这种方法，hash算法的时间复杂度会降低到o(1)，整体时间复杂度为o(n)。  
但是在最坏的情况，hash冲突比较多，每一次还需要子串和模式串进行对比，此时的时间复杂度仍是o(m*n)

代码示例

void RK(char* s, char* p) {
    bool findFlag = false;
    //计算p的hashcode
    int hashP = 0;
    for(int i = 0; p[i]; i++) {
        hashP += (p[i]-'a');
    }
    
    int hashS = 0;
    for(int j = 0; j <= strlen(s)-strlen(p); j++) {
        if(j==0) {
            //计算第一次子串的hashcode
            for(int i = 0; i < strlen(p); i++) {
                hashS += s[i]-'a';
            }
        }else {
            //计算后续子串的hashcode
            hashS = hashS - (s[j-1]-'a') + (s[j+strlen(p)-1]-'a');
        }
        if(hashS == hashP) {
            //hashcode相等时需要对子串和模式串进行验证
            int startS = j, startP = 0;
            while(startP != strlen(p)) {
                if(s[startS] == p[startP]) {
                    startS++;
                    startP++;
                    if(startP == strlen(p)) {
                        findFlag = true;
                        printf("匹配成功，位置为%d\n", j);
                    }
                }else {
                    break;
                }
            }
        }
    }
    if(!findFlag) {
        printf("匹配失败\n");
    }
}

思路3-KMP算法

在BF算法和RK算法中，都需要依次对比子串和模式串中的值，来确保结果的准确性。那么有没有方法可以降低对比的次数呢？KMP算法就提供了解决方案。

几个概念。

字符串的前缀和后缀

如果字符串A和B，存在A=BS，其中S是任意的非空字符串，那就称B为A的前缀。
例如，”Harry”的前缀包括{”H”, ”Ha”, ”Har”, ”Harr”}，我们把所有前缀组成的集合，称为字符串的前缀集合
    
同样可以定义后缀A=SB， 其中S是任意的非空字符串，那就称B为A的后缀，
例如，”Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”}，然后把所有后缀组成的集合，称为字符串的后缀集合。
要注意的是，字符串本身并不是自己的后缀。

int next[]数组

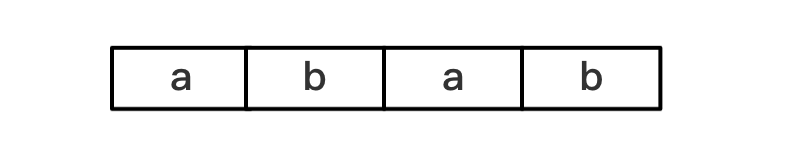
next数组长度和模式串(pattern)长度一致，value为模式字符串到当前索引位置的子串的前缀集合和后缀集合交集中最长元素的长度。

例如：

abab的next数组为：{0,0,1,2}
i=0时，子串为"a"，因为长度只有1，next[0]=0
i=1时，子串为"ab"，前缀合集为{"a"}，后缀为{"b"}，没有交集，next[1]=0
i=2时，子串为"aba"，前缀为{"a","ab"}，后缀为{"a","ba"}，交集为"a"，next[2]=1
i=3时，子串为"abab"，前缀为{"a","ab","aba"}，后缀为{"b","ab","bab"}，交集为"ab"，next[3]=2

至于next数组的求解方法，后面再说，我们先看如何利用next数组进行字符串匹配

先看下图的匹配过程

如果采用暴力法，我们的过程应该为1->2->3->4。

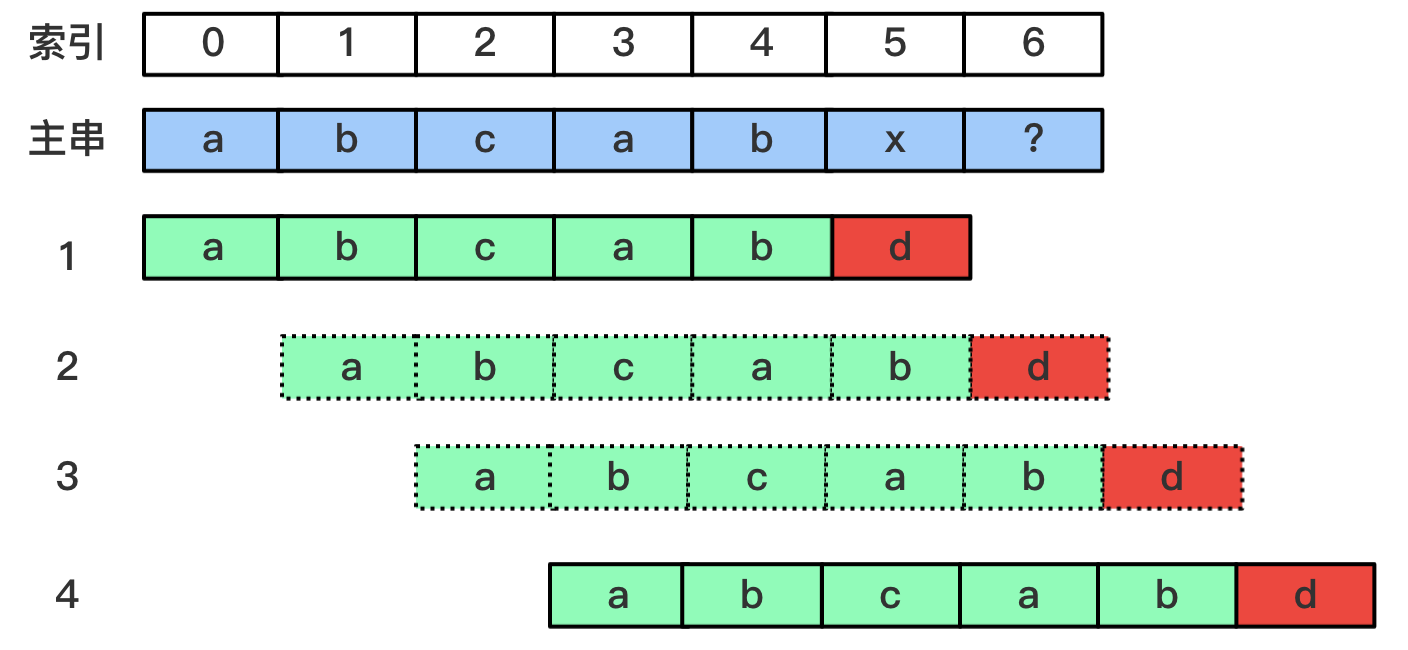
有了next数组，我们的过程为1->4，跳过了步骤2,3

为什么步骤2可以跳过呢？有没有可能步骤2或者3才是正确的匹配路径呢？

我们接下来验证一下。

假如步骤2是正确的匹配路径。那么主串s[1-4]位置的字符应该和模式串p[0-3]中字符一致，为"abca"
因为步骤1中，除了最后一个字符d其他的字符都已经匹配成功，因此模式串中p[1-4]位置的字符应该也是"abca"
综上，模式串中p[0-3]和p[1-4]字符应该是相等的，即模式串中p[0-4]的前缀集合和后缀集合存在长度为3的最长交集。回过头来看next数组的含义，不就是一样的吗。
看一下模式串"abcabd"的next数组为{0,0,0,1,2,0},next[4]的值为2，而上图中跳过匹配不成功的步骤后，能够匹配的步骤中，模式串的索引正好为2。

next数组的求法

假设已知next[i-1]的值为now，即p[0-now)和p[x-1-now，x-1]的值相等，即图中abcab。

此时p[now]==p[x]，则说明next[x]=next[x-1]+1。
p[now]!=p[x]，对比p[next[now-1]]和p[x]。

next数组的优化

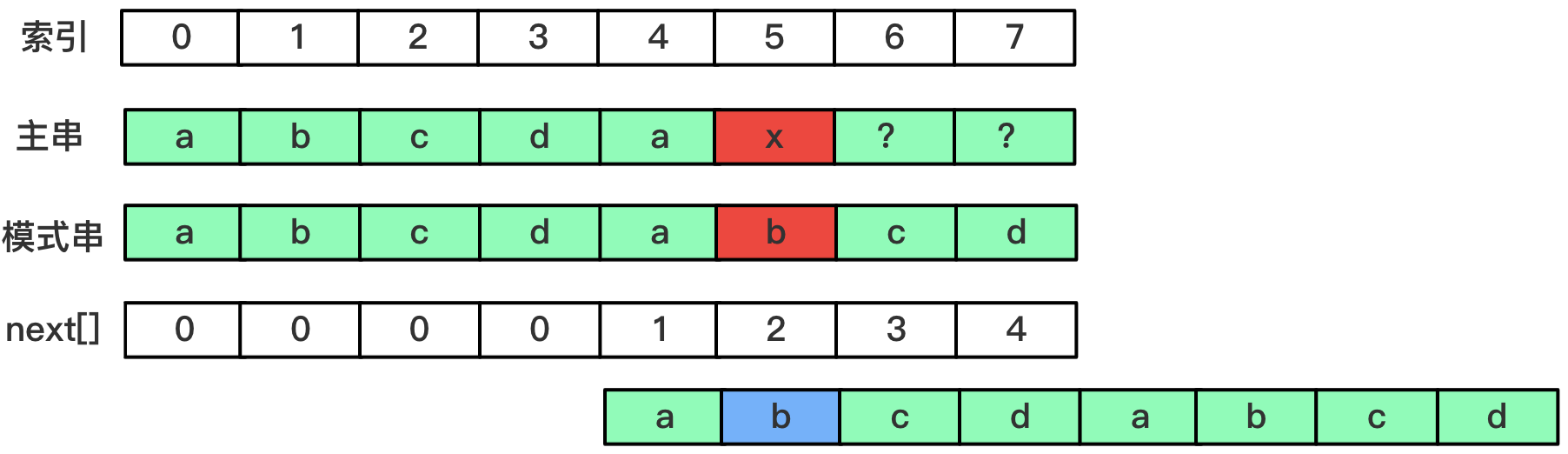
看一下上图的情况，匹配过程中发现字符x和模式串索引5处字符b不相等，根据我们的匹配规则，此时应该将模式串的当前索引移动到next[5-1]即索引为1的位置，此时我们可以发现，因为p[1]和p[5]都为b，相等，显而易见此次匹配也不可能成功，如果我们可以自动跳过这次匹配就好了。

再回头看一下我们next数组的求解

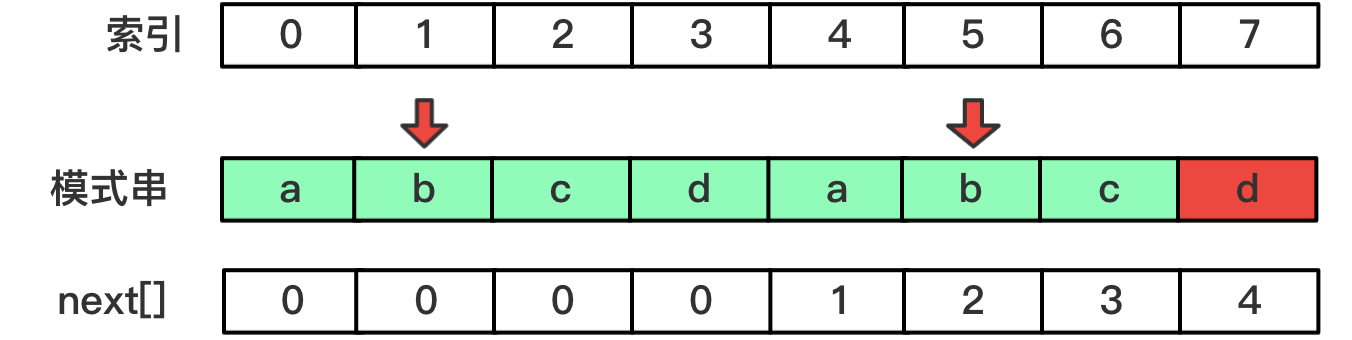
当我们求解next[5]的时候，需要将next[4]位置的字符b和5位置的字符b进行对比，如果相等，则next[5]=next[4]+1。再结合上上图的情况，此时我们不仅求解了next[5]，我们还知道，在字符串匹配的过程中，如果p[5]和s[i](i为匹配过程中主串的索引)匹配失败，我们不需要跳回next[5-1]的位置，因为p[next[5-1]]和p[5]是一样的，也不会和s[i]匹配。

代码

int* getNext(char* p) {
    int len = strlen(p);
    int *next = (int*)malloc(sizeof(int)*len);
    next[0] = 0;
    int i = 1;
    int now = next[i-1];
    while(i < len) {
        if(p[i] == p[now]) {
            now++;
            next[i] = now;
            /*
             此处为优化代码
             if(next[i-1] != 0) {
                 next[i-1] = next[next[i-1]-1];
             }
             */
            i++;
        }else {
            if(now != 0) {
                now = next[now-1];
            }else {
                next[i] = 0;
                i++;
            }
        }
    }
    return next;
}

void KMP(char* s, char* p) {
    bool findFlag = false;
    int *next = getNext(p);
    int i = 0;
    int j = 0;
    while(i < strlen(s)) {
        if(s[i] == p[j]) {
            i++;
            j++;
            if(j == strlen(p)) {
            printf("匹配成功，位置为%2d\n", i-j);
            findFlag = true;
            j = next[j-1];
        }
        }else {
            if(j != 0) {
                j = next[j-1];
            }else {
                i++;
            }
        }
    }
    if(!findFlag) {
        printf("匹配失败\n");
    }
}

获取next数组的时间复杂度为o(m)，匹配的时间复杂度为o(n)，整个算法的时间复杂度为o(m+n)。

字符串匹配算法

描述