爬楼梯算法-js

本人大三学生，js萌新一枚，希望这篇文章可以给各位小白带来一些帮助，也欢迎各位大佬多多指点。话不多说我们步入正题，一起来看看爬楼梯算法。

我们先来阅读题目

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

---

依照题目我们不难看出，假设楼梯有n阶，当我们爬完楼梯的时候，最后总是跨一步或者跨两步

看到这里是否想起了我们的递归，我们直接上代码来看一看：

function climbStairs(n) {
    if (n == 1 || n == 2) return n;
    return climbStairs(n-1) + climbStairs(n-2);
}

做到这里，问题已经解决了，但是递归是否会出现什么问题呢？我们可以想想递归是如何来解决这个算法的。 当我们算4阶楼梯的时候。它是这样实现的：

我们发现使用递归时，它会反复调用函数，直到出现终止条件，这产生了重复计算；当阶梯数很小的时候，或许给我们的感觉不太明显。但是如果阶梯数为100呢？这样重复计算就会造成时间复杂度过高，那么我们是否可以优化一下代码呢。比如不使用递归。

---

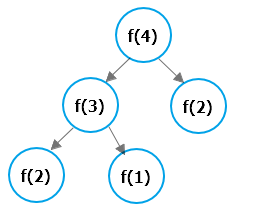
回到之前的想法：假设最后跨1阶，爬之前的台阶的方法为n-1阶楼梯的方法；如果跨2阶，那么爬之前的台阶就有n-2阶楼梯的方法。我们可以假设爬楼梯的方法函数为f();台阶数为n;那么：f(n)=f(n-1)+f(n-2);其实可以发现，随着楼梯数n的增加，爬法总数呈现斐波那契数列规律增加。那么我们是否可以设置爬一阶楼梯的方法为1，爬二阶楼梯的方法为2.这样当台阶数>2时，我们只需要循环相加就可以了。

    function f(n) {
    if (n == 1) return 1;
    if (n == 2) return 2;
    let ret = 0,
        pre = 2,
        prepre = 1; 
    for (let i = 3; i <= n; i++) {
        ret = pre + prepre; //当前楼梯数方法总是前两个楼梯数方法之和
        prepre = pre;
        pre = ret;  
    }
    return ret;
}

看到这里是否有些感觉了呢？