小白笔记：js中斐波那契数列的实现与两种优化思路

本人是一名前端的初学者，将不定时分享一些自己在学习过程中的想法，希望我的文章能对你有所帮助，若你发现文章之中存在某些错误或让你疑惑的位置，也欢迎大家在评论区指出，让我们一起讨论，共同进步！

无论把责任归咎于谁，到头来决定一切的还是自己。 --JOE 《MEGALO BOX》

1.什么是斐波那契数列

斐波那契数列（Fibonacci sequence） 又称黄金分割数列、因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(1)=1，F(2)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 3，n ∈ N*）

• 以上是度娘给的解释，可见斐波那契数列的特点是前面相邻两项之和等于后一项的值且初始两项值为1，接下来让我们来看看它在js语言中的表达形式。

2.js中斐波那契数列的表达形式

2.1 基本表达式

由该数列的公式可知由递推公式得出

let fib = function (n) {
    if(n === 1 || n === 2){
        return 1;
    }
    return fib(n-1) + fib(n-2);
  };

2.2 检测性能

• 加入一个变量redo记录fib方法被调用的次数，用for循环打印数组并输出fib调用次数redo

let redo = 0;
let fib = function (n) {
    redo++; 
    if(n === 1 || n === 2){
        return 1;
    }
    return fib(n-1) + fib(n-2);
  };
  for (let i = 1; i <= 10; i++){
    console.log(i + ':' +  fib(i) + '     fib调用次数：' + redo);
  }

得到控制台输出

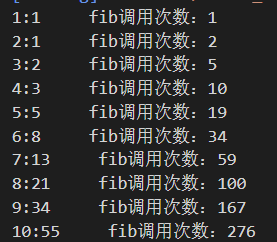
• 从输出结果中可看出这样确实可已得到我们想要的斐波那契数列，但这样程序做了太多的无用功。fib方法一共被调用了276次，我们为得到数组调用了10次，而它自身重复调用了266次去计算可能已经被计算过的值。那我们是不是可以对其进行优化呢？

3.优化算法

3.1.1 优化思路1：记忆

• 该算法是因为无法知道函数已经得出了前两项的值而重复计算，那么我们是不是可以给其加上记忆前两项值的功能使其能够大大减少重复调用的次数。

3.1.2 优化思路1实现

• 在一个名为memerize的数组里保存相邻前两项的值，当fib被调用时，先检查结果是否已存在，如果已存在，就返回结果。

let redo = 0;
let memorize = [1,1];
let fib = function (n) {
    redo++; 
    if(typeof memorize[n] != 'number'){
        return  memorize[n]=fib(n-1) + fib(n-2);
    }
    return memorize[n]
  };
  for (let i = 0; i <= 10; i++){
    console.log(i + 1 + ':' +  fib(i) + '     fib调用次数：' + redo);
  }

tips：数组中第一个元素的下标为0

得到控制台输出

• 可以看到优化后的程序性能大大提高，fib方法的调用次数共需29次，为得到结果重复了10次，它调用自己去取得之前的的存出结果重复了19次。

3.2.1 优化思路2：循环

• 我们抛开为得到斐波那契数列而从后往前递归推理得到数字的思维，从前往后观察该数列的特点，可以发现，该数列前两项值已知，只要加上一个for循环就可得到第三项从而得到整个数列。

3.2.2 优化思路2实现

• 定义变量pre为前两项中前一项，定义变量prepre为前两项中后一项，定义变量ret作为前两个两项之和的容器，得到ret值后将prepre的值赋给pre，再将ret值付给prepre，运用循环让其滑动起来，从而得到数列。

let redo = 0;
function fib(n) {
    if (n === 1 || n === 2) {
        redo++;
        return 1;
    };
    let ret = 0;
     pre = 1;
     prepre = 1;
     for(let i = 3; i<=n; i++){
        redo++;
         ret = pre + prepre;
         prepre = pre;
         pre = ret;
     }
    return ret;
}
for (let i = 1; i <= 10; i++){
    console.log(i + ':' +  fib(i) + '  fib调用及内部循环次数：' + redo);
  }

得到控制台输出

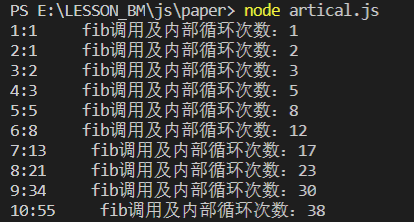
• 可以看到从前往后的推理，运用循环同样可以实现斐波那契数列，为得到结果调用了10次，内部进行循环得到之前计算的结果重复了28次，也大大提升了算法的性能。

4 总结

综上所述，为了解决递归算法会重复调用自己去计算已经得到过的值，本文提出了两种优化的思路，一种是记忆的思路、另一种是运用一个循环来从前往后，顺序的计算出数组。可以看到通过给程序加上记忆的模块或者运用循环的方法都可以大大的简化运用递归创建斐波那契数列所需要的运算量。