队列

队列也是一类特殊的线性顺序结构，它规定仅能在表的一端进行插入操作，这一端称为队尾rear；而数据的访问和删除操作必须在另一端进行，这一端称为队头front。

特殊的操作使得堆栈中的元素满足 FILO （先进先出），如图所示：

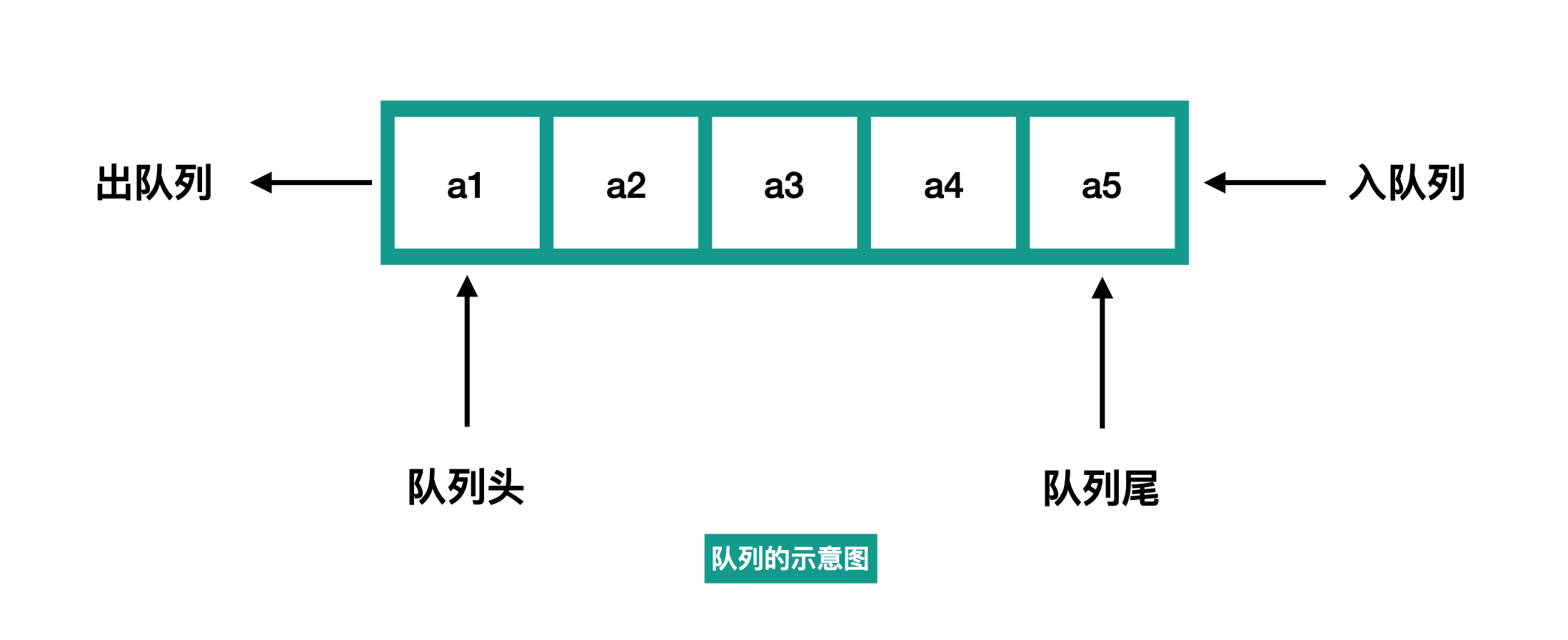
本篇所涉及的代码在这。

队列可以使用顺序存储结构和链式存储结构来实现。

顺序存储结构

顺序队列的实现比较简单，借助一维数组，我们使用标记front和rear来分别标记队头和队尾，然后按照要求进行出入队操作即可，如下图所示：

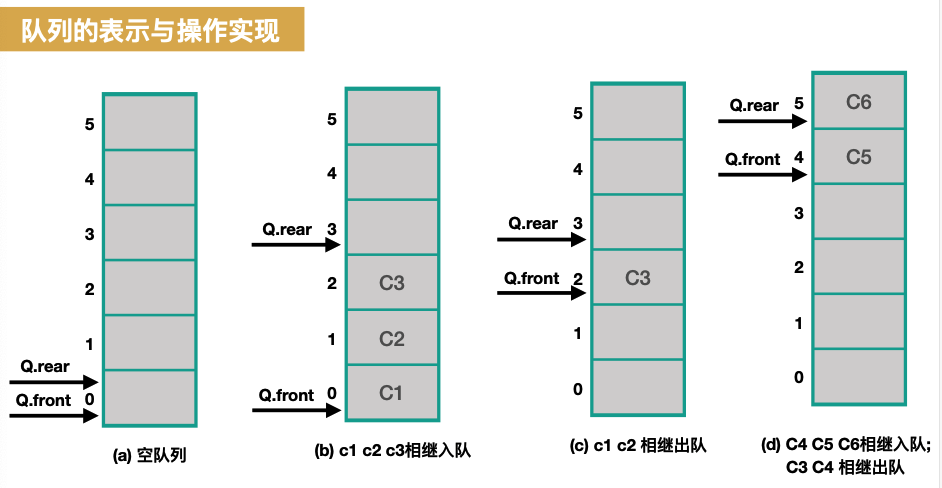
但是这样会引起假溢出。

假溢出：顺序队列在front出栈之后，front的位置会向后移动，导致front之前的空间再也无法被新入队的元素进行使用从而浪费了空间，进而导致队列在还有剩余空间的时候无法再继续入队，这样的现象就叫假溢出。

例如：上图（c）中c1,c2出对之后，front向前移动到数组的2位置，此时0和1俩个位置无法供新入队的元素进行使用了（因为入队总是从rear来进行的），在图d中就出现了假溢出。

循环队列

为了解决上述提到的假溢出问题，我们引入了循环队列。

注意：此处的循环是逻辑结构上的循环而不是存储层面的循环。从逻辑结构上，可以使用下图进行理解：

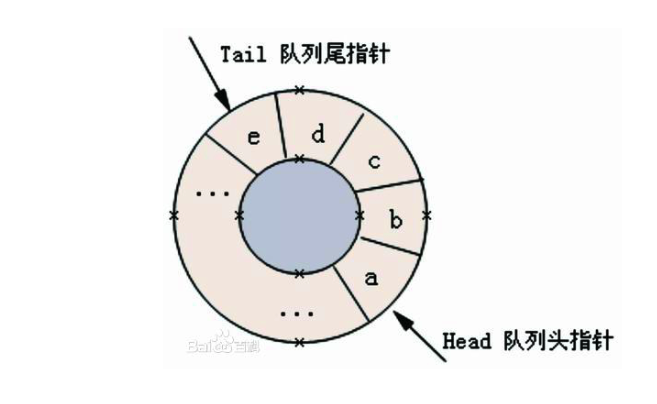
我们可以看到，由于整个结构是一个环状，所以在rear入队之时总是能够将所有的空间都充分使用从而解决了假溢出问题。

通过上图我们不难看出一些状态的判断：

队列空：Head 和 Tail 指针指向同一个位置，此时环内没有任何数据。
队列满：Head 和 Tail 指针指向同一个位置，此时环内装满了数据。

问题来了，队列的两种关键状态的判断条件是一样的，那么从程序上我们就无法分辨队列的真实状态了。

所以我们必须使用新的方法来对这两种状态进行区分。

添加flag标记我们可以使用标记来对队列的状态进行记录，从而解决上述问题。

这样的操作使用了额外的空间，而且我们需要对于标记进行额外管理。

使用空位置进行标记当队满的时候 Head 和 Tail 指向的位置是一样的，那么我们可以空出这个位置。简言之：我们不把队装满，我们规定当队列只有一个空位时，我们就认为队列已经满了。

在这种情况下，队满的判断条件变为：若 Tail + 1 的位置遇见了Head。

小结一下：

判断队空: Head == Tail;
判断队满: (Tail + 1) % MAXSIZE == Head;

从逻辑上我们可以了理解为下图：

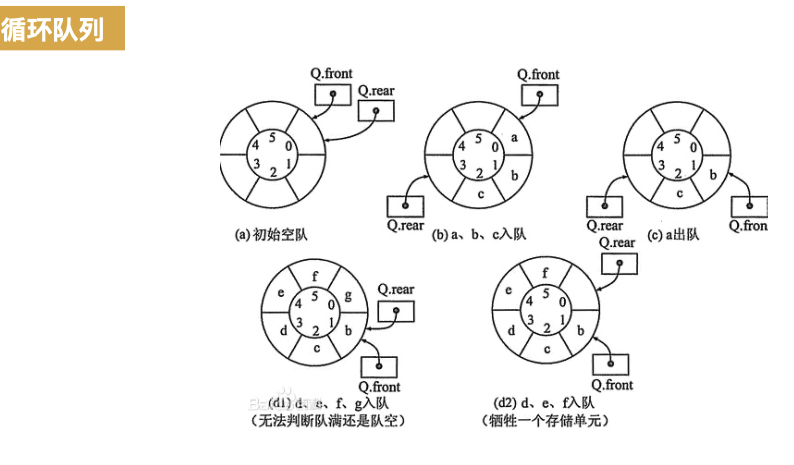
在实际的内存中的情况如下图所示：

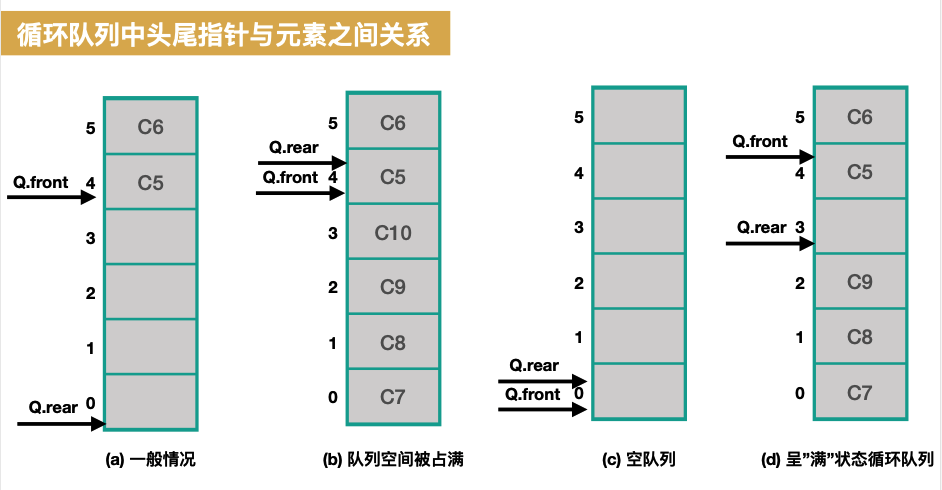
顺序方式实现队列

特别说明：经过上述讨论我们已经知道了单纯的顺序队列存在假溢出的问题，所以一般地，没有特别说明时，我们提到顺序队列你就要清楚我们说的是循环队列。

定义

顺序结构下我们需要对队列的结点进行定义，这里还定义了一些必要的状态和常数。


#define MAXSIZE 20

#define SUCCESS 1
#define ERROR 0

#define TRUE 1
#define FALSE 0

typedef int ElementType;

typedef int Status;

//定义顺序队列
typedef struct LinearQueue{
    //    数据域
    ElementType data[MAXSIZE];
    //    队头 出队在此处进行
    int front;
    //    队尾 入队在此进行
    int rear;
}LinearQueue;

初始化

顺序结构下的队列是借助一维数组来实现的。

这里还实现了一些辅助功能，例如：队列的判空，获取队列长度等。

初始化


/// 队列的初始化
/// @param q 队列
Status queueInit(LinearQueue *q){
    q->front = q->rear = 0;
    return SUCCESS;
}

清空队列


/// 清空队列
/// @param q 队列
Status queueClear(LinearQueue *q){
    q->front = q->rear = 0;
    return SUCCESS;
}

获取队列的长度


/// 获取队列的长度
/// @param q 队列
int queueGetCount(LinearQueue q){
    //    注意循环可能会出现负数，所以需要 + MAXSIZE
    return (q.rear + MAXSIZE - q.front) % MAXSIZE;
}

判断队列是否为空


/// 判断队列是否为空
/// @param q 队列
Status queueIsEmpty(LinearQueue q){
    return 0 == queueGetCount(q);
}

判断队列是否满


/// 判断队列是否满了
/// @param q 队列
Status queueIsFull(LinearQueue q){
    return q.front == (q.rear + 1) % MAXSIZE;
}

遍历并输出队列


/// 遍历并输出队列
/// @param q 队列
Status queuePrint(LinearQueue q){
    if (queueIsEmpty(q)) {
        printf("队列为空！\n");
        return ERROR;
    }
//    printf("从front开始倒序输出元素，这个顺序就是入队的顺序，也是将来出队的顺序。");
    printf("\n队列元素：");
    for (int i = 0; i < queueGetCount(q); i++) {
        int index = ((q.front + i) % MAXSIZE);
        ElementType e = q.data[index];
        printf("%d, ", e);
    }
    printf("\n\n");
    return SUCCESS;
}

入队

顺序结构下的入队需要注意对队满状态需要容错，同时注意对rear的操作。


/// 入队
/// @param q 队列
/// @param e 入队元素
Status queueIn(LinearQueue *q, ElementType e){
    if (queueIsFull(*q)) {
        printf("队列已经满了！\n");
        return ERROR;
    }
    q->data[q->rear] = e;
    q->rear = ((q->rear + 1) % MAXSIZE);
    return SUCCESS;
}

出队

顺序结构下的出队需要注意对队空状态需要容错，同时注意对front的操作。


/// 出队
/// @param q 队列
/// @param e 出队元素带回
Status queueOut(LinearQueue *q, ElementType *e){
    if (queueIsEmpty(*q)) {
        printf("队列已经空了！\n");
        return ERROR;
    }
    *e = q->data[q->front];
    q->front = (q->front + 1) % MAXSIZE;
    return SUCCESS;
}

链式结构队列

由于链式结构的结点是动态生成的，不存在浪费空间的情况，也就没有假溢出的说法了，所以链式结构下的队列理解起来十分简单。如图所示：

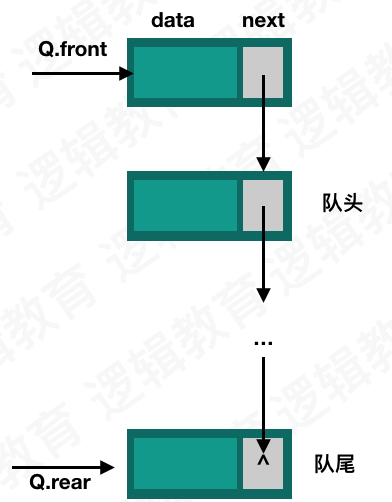
定义

链式结构下我们需要对队列的结点进行定义，这里还定义了一些必要的状态和常数。


//对于链式队列理论上来说长度是无限的。不过你也对其最大长度进行限定。
#define MAXSIZE 20

#define SUCCESS 1
#define ERROR 0

#define TRUE 1
#define FALSE 0

typedef int ElementType;
typedef int Status;

//定义队列结点类型，以及指向此类型的指针类型
typedef struct QueueNode{
    ElementType data;
    struct QueueNode *next;
}QueueNode, *QueueNodePtr;

typedef struct ChainQueue{
//    队头 结点从这里出队
    QueueNodePtr front;
//    队尾 结点从这里入队
    QueueNodePtr rear;
//    队列的长度
    int count;
}ChainQueue;

初始化

对于队列的初始化我们可以添加头结点，这样在入队时的操作更加统一，不需要对首元结点进行额外的处理。

这里还实现了一些辅助功能，例如：队列的判空，获取队列长度等。

初始化


/// 初始化
/// @param q 队列
Status queueInit(ChainQueue *q){
//    注意：这里使用了头结点，当然你也可以不用┗|｀O′|┛ 嗷~~
    q->rear = q->front = (QueueNodePtr)malloc(sizeof(QueueNode));
    q->count = 0;
    return SUCCESS;
}

队列判空


/// 判断队列是否为空
/// @param q 队列
Status queueIsEmpty(ChainQueue q){
//    当然此处你也可以使用 count 进行判空
    return q.rear == q.front;
}

获取队列的长度


/// 获取队列的长度
/// @param q 队列
int queueGetCount(ChainQueue q){
    return q.count;
}

清空队列


/// 清空队列
/// @param q 队列
Status queueClear(ChainQueue *q){
    QueueNodePtr temp;
//    p = q->front;
    while (q->front) {
        temp = q->front;
        q->front = q->front->next;
        free(temp);
    }
//    注意这里：front的位置和长度都需要处理，或者在函数内直接使用front跳步也行(代码改了，采用的这种方法)。
//    q->front = p;
    q->count = 0;
    return SUCCESS;
}

遍历输出队列


/// 遍历输出队列
/// @param q 队列
Status queuePrint(ChainQueue q){
    if (queueIsEmpty(q)) {
        printf("队列为空，无法输出！\n");
        return ERROR;
    }
    
//    输出的时候不能改变的原结构，所以不能使用队列的指针进行跳步，使用临时指针 p 进行操作。
    QueueNodePtr p;
    p = q.front->next;
    
    printf("队列信息：");
    while (p) {
        printf("%d, ", p->data);
        p = p->next;
    }
    printf("\n\n");
    return SUCCESS;
}

入队

入队操作就是在链表的尾部加入新的结点即可，注意对rear和count的处理。


/// 入队
/// @param q 队列
/// @param e 待入队的元素
Status queueIn(ChainQueue *q, ElementType e){
    
//    如果你限定了最大长度，你需要在此处进行容错判断。
    
    QueueNodePtr k;
    
//    准备入队的结点
    k = (QueueNodePtr)malloc(sizeof(QueueNode));
    k->data = e;
    k->next = NULL;
//    入队
    q->rear->next = k;
    q->rear = k;
//    长度处理
    q->count++;
    
    return SUCCESS;
}

出队

出队操作可以理解为删除链表首元结点，注意对头结点和count的处理。


/// 出队
/// @param q 队列
/// @param e 出队元素带回
Status queueOut(ChainQueue *q, ElementType *e){
    if (queueIsEmpty(*q)) {
        printf("队列为空，无法出队！");
        return ERROR;
    }
    
    QueueNodePtr temp;
    
//    注意本例是使用了头结点的。所以需要留意此处对于头结点的处理。
    temp = q->front->next;
    q->front->next = q->front->next->next;
//    带回出队结点的值并释放该结点
    *e = temp->data;
    free(temp);
//    长度处理
    q->count--;
    
    return SUCCESS;
}

小结

对于队列，最主要的就是理解它FIFO的思想。类似于堆栈一样，这样的思想也可以使用在某些特殊场景的解题思路中，而不单单是一种数据结构的实现。

【学习记录】队列 20200413

队列

顺序存储结构

循环队列

顺序方式实现队列

定义

初始化

入队

出队

链式结构队列

定义

初始化

入队

出队

小结