数据结构学习笔记-05 栈-> 和 . 大问题能拆成小问题，但是大问题解决的方法和小问题解决的方法相同或者大部分相同。e

结构划分概念

逻辑结构：线性结构、集合结构、树形结构、图形结构
物理结构：顺序储存结构、链式结构

-> 和 .

如果是指针 *p->data
如果是对象 p.data

顺序栈

#include <stdio.h>
#include "stdlib.h"

#include "math.h"
#include "time.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存储空间初始分配量 */

typedef int Status;
typedef int Element;


/*顺序结构*/
typedef struct {
    Element data[MAXSIZE];
    int top;//用于指向栈顶
}Stack;

//1.构建空栈
Status initStack(Stack *S) {
    S->top = -1;//以-1代表空战
    return OK;
}

//2.栈置空
Status nilStack(Stack *S) {
    //栈置空不需要将栈里面的元素清空，只需要修改top就行，因为数组空间已开始就已经分配了
    S->top = -1;
    return OK;
}

//3.判断栈是否为空
Status empty(Stack S) {
    if (S.top == -1) {
        return OK;
    } else {
        return ERROR;
    }
}

//栈长
int lengthStack(Stack S) {
    return S.top + 1;
}

//获取栈顶
Status queryTopStack(Stack S,Element *e) {
    if (S.top == -1) {
        return ERROR;
    } else {
        *e = S.data[S.top];
        return OK;
    }
}

//.push
Status push(Stack *S,Element e) {
    //满了
    if (S->top == MAXSIZE-1) {
        printf("！！！stack is full");
        return ERROR;
    } else {
        //栈顶指针+1;
        S->top ++;
        //将新插入的元素赋值给栈顶空间
        S->data[S->top] = e;
        
//        S->data[S->top + 1] = e;
//        S->top = S->top + 1;
        return OK;
    }
}


//pop
Status pop(Stack *S,Element *e) {
    if (S->top == -1) {
        printf("！！！stack is empty");
        return ERROR;
    } else {
        //将要删除的栈顶元素赋值给e
        *e = S->data[S->top];
        //栈顶指针--;
        S->top --;
        return OK;
    }
}

//遍历 从栈底到栈顶依次对栈中的每个元素打印
Status traverse(Stack S) {
    if (S.top == -1) {
        printf("！！！stack is empty");
        return ERROR;
    }else {
        for (int i = 0; i < S.top; i ++) {
            printf("%d,  ",S.data[i]);
        }
        printf("\n");
        return OK;
    }
}


int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, World!\n");
    
    
    //测试
    Stack S;
    //新建空栈
    Status status = initStack(&S);
    traverse(S);
    //空栈判断
    Status isEmpty = empty(S);
    
    //push
    if (status) {
        for (int j = 1; j < 10; j ++) {
            push(&S,j);
        }
    }
    traverse(S);
    
    //获取栈顶
    Element e;
    queryTopStack(S, &e);
    
    //pop
    pop(&S, &e);
    traverse(S);
    
    //栈长
    int length = lengthStack(S);
    
    //置空
    nilStack(&S);
    traverse(S);
    
    return 0;
}

链式栈

#include <stdio.h>
#include "stdlib.h"

#include "math.h"
#include "time.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存储空间初始分配量 */


typedef int STATUS;
typedef int ELEMENT;

//链式栈结构节点
typedef struct StackNode{
    ELEMENT data;
    struct  StackNode *next;
}StackNode, *LinkStackPtr;

typedef struct {
    LinkStackPtr top;//指向栈顶的指针
    int count;//数量
}LinkStack;



//构造一个空栈
STATUS StackInit(LinkStack *S) {
    S->top = NULL;
    S->count = 0;
    return OK;
}

//置空链栈
STATUS StackClear(LinkStack *S) {
    LinkStackPtr p,q;
    p = S->top;
    while (p) {
        //保存当前节点
        q = p;
        //下一个
        p = p->next;
        //释放当前节点
        free(q);
    }
    //释放完后
    S->count = 0;
    return OK;
}

//是否为空栈
STATUS StackIsEmpty(LinkStack S) {
    if (S.count == 0) {
        return TRUE;
    } else {
        return FALSE;
    }
}

//获取栈顶
STATUS StackTop(LinkStack S,ELEMENT *e) {
    if (S.top == NULL) {
        return ERROR;
    } else {
        *e = S.top->data;
        return OK;
    }
}

//链长:元素的个数
int StackLenght(LinkStack S) {
    return S.count;
}

//push
STATUS StackPush(LinkStack *S,ELEMENT e) {
    //创建新的节点
    LinkStackPtr temp = (LinkStackPtr)malloc(sizeof(StackNode));
    //赋值
    temp->data = e;
    //把当前的栈顶元素赋值给新结点的直接后继,
    temp->next = S->top;
    //将新结点temp 赋值给栈顶指针
    S->top = temp;
    //count +1
    S->count++;
    return OK;
}

//pop
STATUS StackPop(LinkStack *S,ELEMENT *e) {
    if (S->top == NULL) {
        return ERROR;
    }
    //将栈顶结点赋值给p
    LinkStackPtr temp;
    temp = S->top;
     
    //将栈顶元素赋值给*e
    e = &S->top->data;
    //使得栈顶指针下移一位, 指向后一结点.
    S->top = S->top->next;
    //count-1
    S->count--;
    //释放节点空间
    free(temp);
    
    return OK;
}

//遍历链栈
STATUS StackTraverse(LinkStack S) {
    LinkStackPtr p = S.top;
    while (p) {
        printf("%d ",p->data);
        p = p->next;
    }
    printf("\n");
    return OK;
}

int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, World!\n");
    
    int j;
    LinkStack s;
    int e;
    if(StackInit(&s)==OK)
        for(j=1;j<=10;j++)
            StackPush(&s,j);
    printf("栈中元素依次为：");
    StackTraverse(s);
    StackPop(&s,&e);
    printf("弹出的栈顶元素 e=%d\n",e);
    StackTraverse(s);
    printf("栈空否：%d(1:空 0:否)\n",StackIsEmpty(s));
    StackTop(s,&e);
    printf("栈顶元素 e=%d 栈的长度为%d\n",e,StackLenght(s));
    StackClear(&s);
    printf("清空栈后，栈空否：%d(1:空 0:否)\n",StackIsEmpty(s));
    return 0;
}

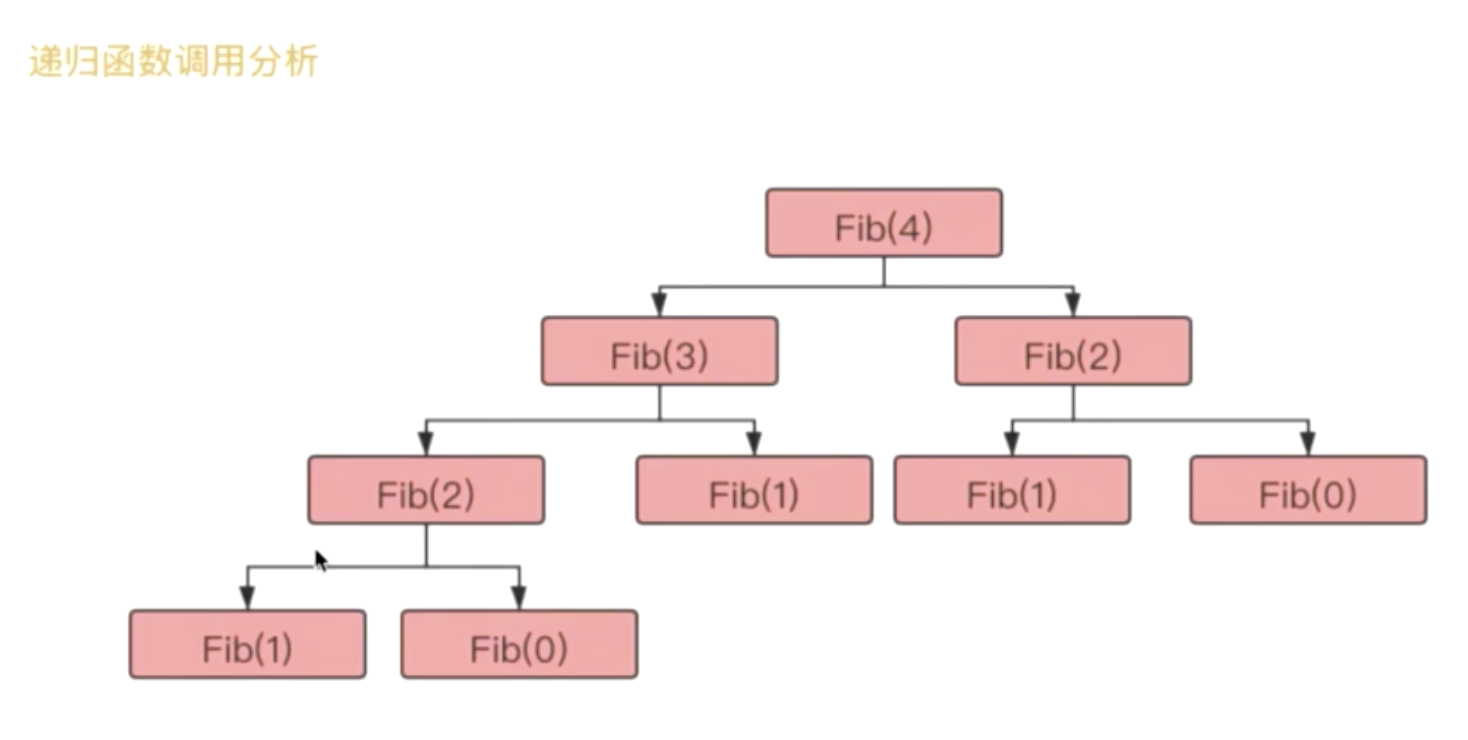
递归工作栈

数据结构是不是递归？链表是不是递归？问题是不是递归？如果有一项是，就可以采用递归

分治法

大问题能拆成小问题，但是大问题解决的方法和小问题解决的方法相同或者大部分相同。eg：n!阶乘。求10! 就要求10*9!,求9! 就要求9*8!
拆完之后，问题会简单
必须有一递归的出口(边界)

斐波那契数列

#include <stdio.h>

int Fbi(int i){
    if(i<2)
        return i == 0?0:1;
    return Fbi(i-1)+Fbi(i-2);
}

int main(int argc, const char * argv[]) {
    // insert code here...
    printf("斐波拉契数列!\n");
    // 1 1 2 3 5 8 13 21 34 55 89 144
    for (int i =0; i < 10; i++) {
         printf("%d  ",Fbi(i));
    }
    printf("\n");
   
    return 0;
}

斐波那契数列的算法实现会开辟大量的空间，并且空间的数据结构和栈很相似