前言
前几篇我们说到数据结构有两种:逻辑结构和存储结构;那怎么样可以更好的理解这两种结构呢?以下是我个人的一些见解,如果不妥,请勿采纳。
逻辑结构:包括集合结构(元素之间没有关系),线性结构(元素之间一对一的关系),树形结构(元素之间一对多的关系),图形结构(元素之间多对多的关系),就像我们小时候都有各自的理想,比如当医生,老师,科学家等等,属于目标或者说是名词。
存储结构:包括顺序存储,链式存储,就像是我们可以通过好好学习等方式来实现我们从小的梦想。
今天我们就来用顺序存储和链式存储来实现线性结构中的栈结构。
栈
栈(stack)又名堆栈,它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。也就是我们常说的先入后出(FILO)结构。
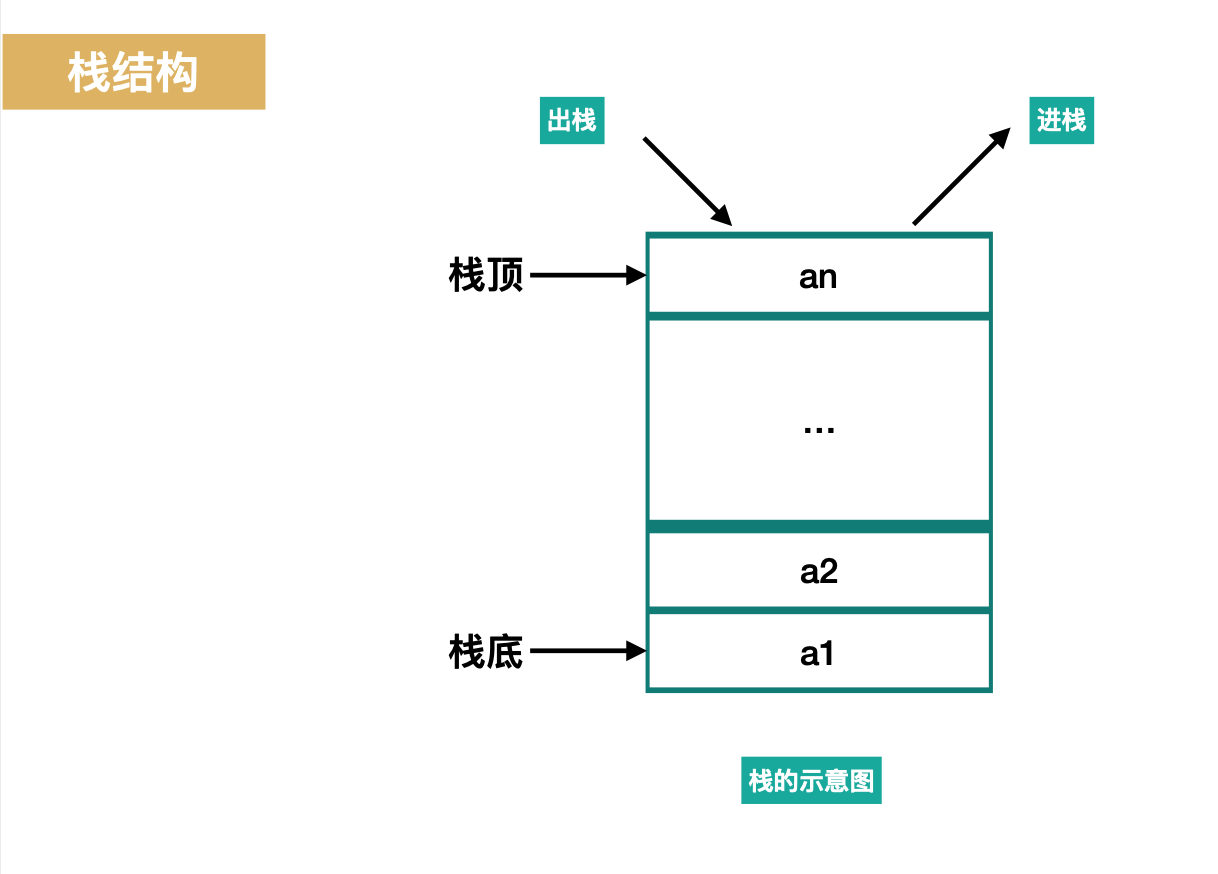
顺序存储实现栈
顺序存储结构: 数据元素存放在一组存储地址连续的存储单元里,其数据元素间的逻辑关系和物理关系是一致的。
- 创建空栈
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存储空间初始分配量 */
typedef int Status;
typedef int ElemType; /* ElemType类型根据实际情况而定,这里假设为int */
typedef struct
{
ElemType data[MAXSIZE]; // 开辟一段连续的存储地址
int top; // 用于栈顶指针
}Stack;
// 创建一个空栈
Status initStack(Stack *S)
{
S->top = -1;
return OK;
}
- 清空栈
// 清空栈
Status clearStack(Stack *S)
{
// 只需要修改top标签置位-1就可以了.
S->top = -1;
return OK;
}
- 入栈(进栈,压栈)
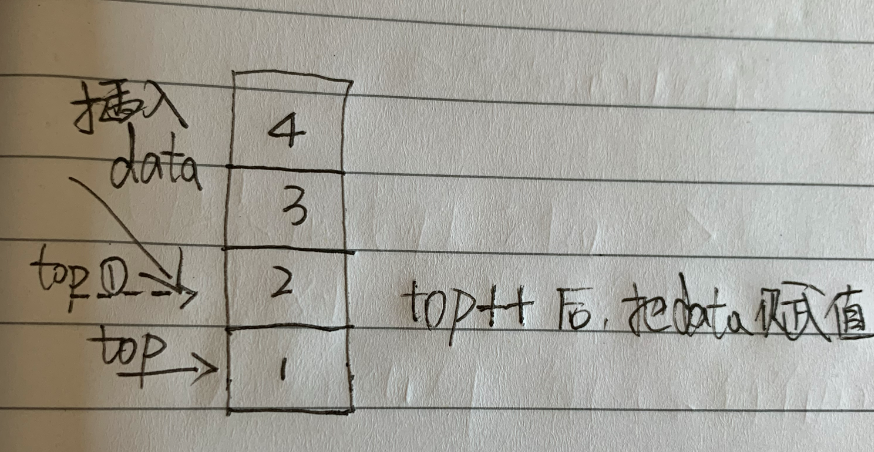
// 入栈
Status pushStack(Stack *S,ElemType data)
{
// 先判断栈是否已满
if (S->top == MAXSIZE - 1) {
return ERROR;
}
// 从栈尾插入数据,栈顶指针top + 1
S->top ++;
// 将新插入的数据放到栈顶
S->data[S->top] = data;
return OK;
}
- 出栈(退栈)
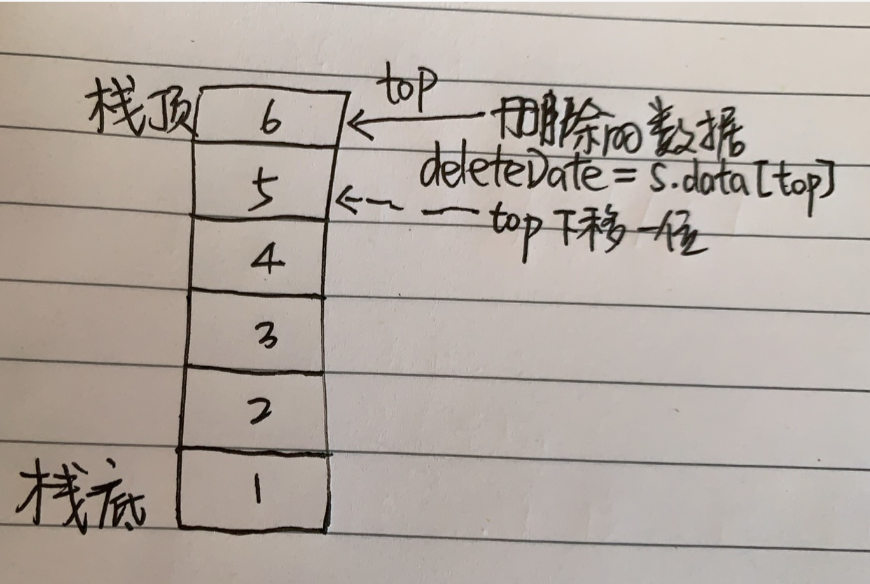
// 出栈
Status popStack(Stack *S, ElemType *deleteData)
{
// 判断栈是否是空栈
if (S->top == -1) {
return ERROR;
}
// 返回要删除的数据
*deleteData = S->data[S->top];
// 栈顶指针top --
S->top --;
return OK;
}
- 打印栈元素
// 打印栈
Status printStack(Stack S)
{
printf("栈中的元素:");
for (int i = 0; i <= S.top; i ++) {
printf("%d",S.data[i]);
printf("\n");
}
return OK;
}
在顺序存储中,栈的栈顶指针是最重要的标志,入栈,出栈主要是栈顶指针移动,数据插入删除的过程。
链式存储实现栈
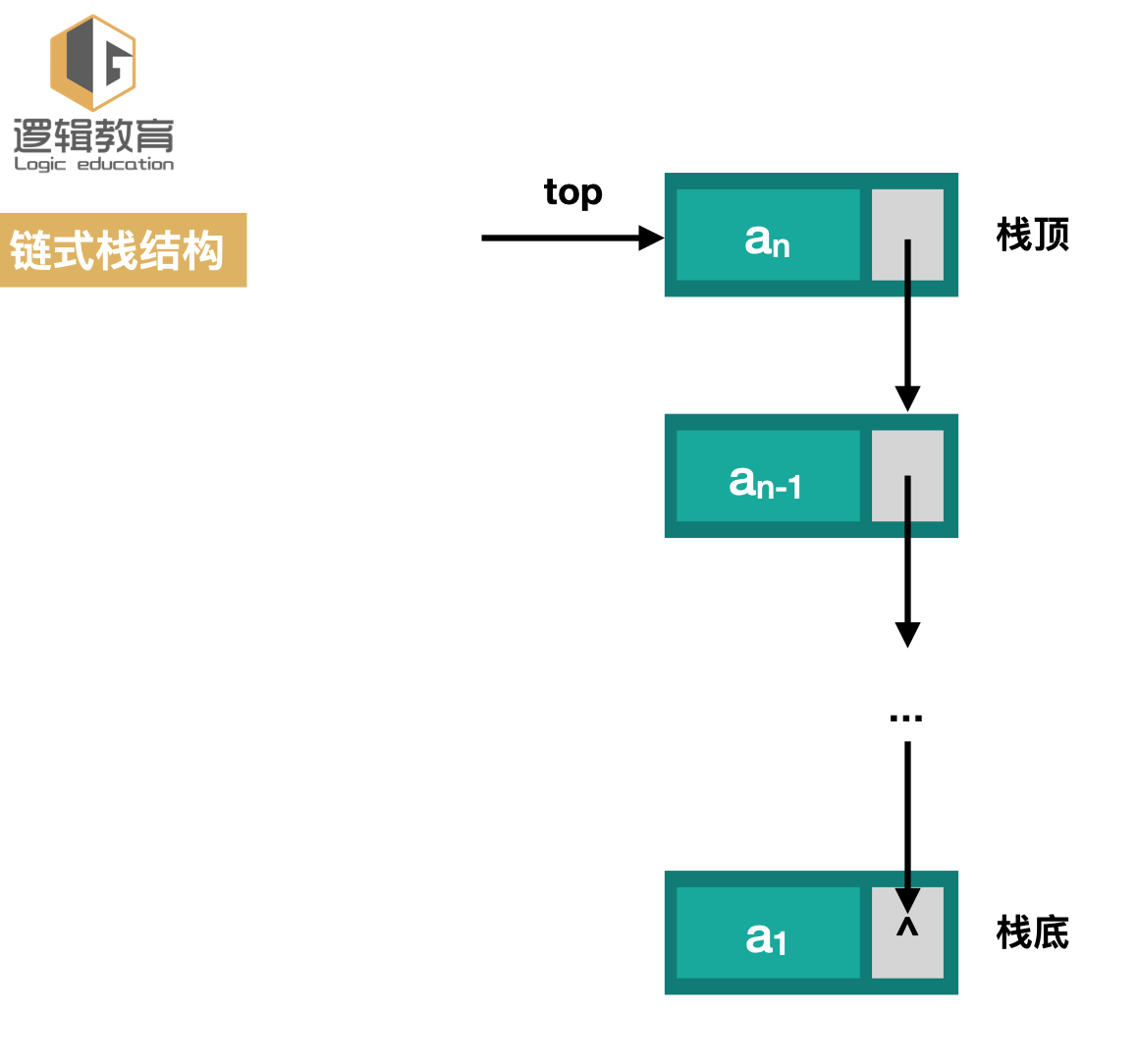
单链表结构实现栈,栈顶top,next指向下一个结点,栈底结点的next指向空。
- 定义栈
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存储空间初始分配量 */
typedef int Status;
typedef int ElemType; /* ElemType类型根据实际情况而定,这里假设为int */
// 栈里的结点
typedef struct
{
ElemType data;
struct stackNode *next;
}stackNode, *linkStackNode;
// 链式栈结构
typedef struct
{
linkStackNode top; // 固定不动的,使用链式的next指向的指针
int count;
}linkStack;
- 创建空栈
// 创建一个空栈
Status initLinkStack(linkStack *S){
S->top = NULL;
S->count = 0;
return OK;
}
- 清空栈
// 清空栈
Status clearLinkStack(linkStack *S){
// 定义两个变量,记录释放的指针和头指针
linkStackNode tempNode,top;
top = S->top;
while (top) {
tempNode = top; // 从栈顶开始释放
top = top->next;
free(tempNode);
}
return OK;
}
- 判断是否为空栈
// 判断是否为空栈
Status isEmptyStack(linkStack S){
if (S.count == 0) {
return TRUE;
}
return FALSE;
}
- 获取栈顶元素
// 获取栈顶元素
Status getTop(linkStack S, ElemType *topData){
if (S.top == NULL) {
return ERROR;
}
*topData = S.top->data;
return OK;
}
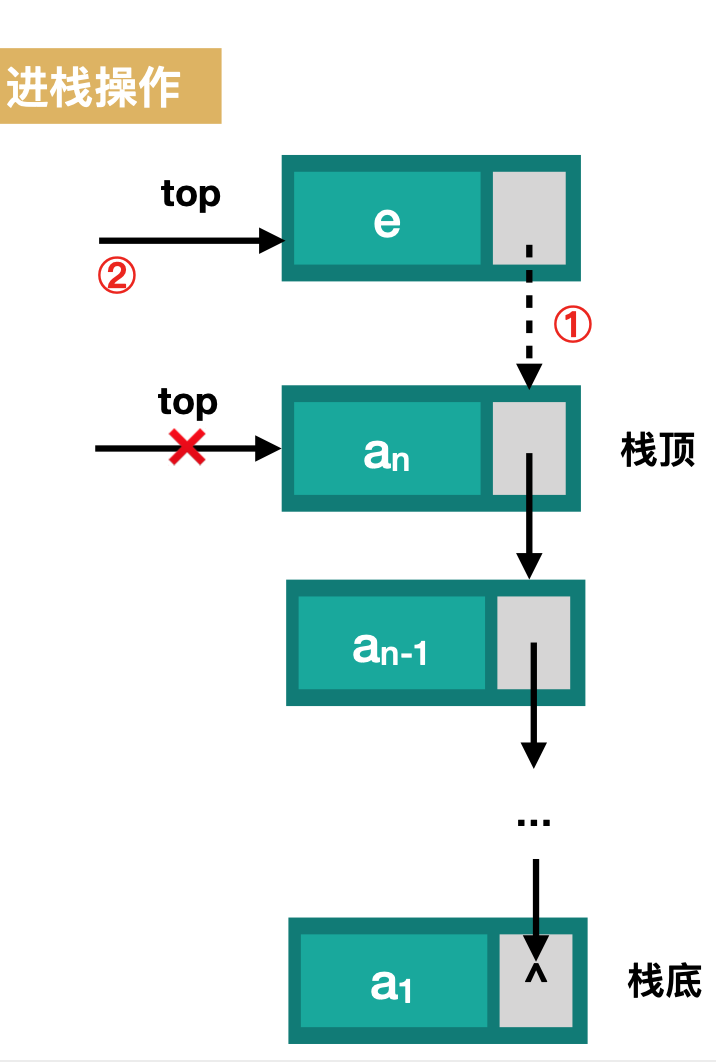
- 入栈
// 入栈
Status pushLinkStack(linkStack *S,ElemType data){
// 创建一个新结点
linkStackNode temp = (linkStackNode)malloc(sizeof(stackNode));
// 赋值
temp->data = data;
// 把当前的栈顶元素赋值给新结点的直接后继
temp->next = S->top;
// 把top上移
S->top = temp;
// 栈的个数++
S->count ++;
return OK;
}
- 出栈
// 出栈
Status popLinkStack(linkStack *S,ElemType *data){
// 判断是否空栈
if (isEmptyStack(*S)) {
return ERROR;
}
linkStackNode temp = S->top;
*data = temp->data;
// top下移一位
S->top = temp->next;
// 释放原top指针
free(temp);
// 个数递减
S->count--;
return OK;
}
- 打印栈
Status printLinkStack(linkStack S){
linkStackNode temp = S.top;
while (temp) {
printf("%d ",temp->data);
temp = temp->next;
}
printf("\n");
return OK;
}
int main(int argc, const char * argv[]) {
// insert code here...
printf("链栈定义与实现\n");
int j;
linkStack s;
int e;
if(initLinkStack(&s)==OK)
for(j=1;j<=10;j++)
pushLinkStack(&s,j);
printf("栈中元素依次为:");
printLinkStack(s);
popLinkStack(&s,&e);
printf("弹出的栈顶元素 e=%d\n",e);
printLinkStack(s);
printf("栈空否:%d(1:空 0:否)\n",isEmptyStack(s));
getTop(s,&e);
printf("栈顶元素 e=%d 栈的长度为%d\n",e,s.count);
clearLinkStack(&s);
printf("清空栈后,栈空否:%d(1:空 0:否)\n",isEmptyStack(s));
return 0;
}
运行结果:
链栈定义与实现
栈中元素依次为:10 9 8 7 6 5 4 3 2 1
弹出的栈顶元素 e=10
9 8 7 6 5 4 3 2 1
栈空否:0(1:空 0:否)
栈顶元素 e=9 栈的长度为9
清空栈后,栈空否:1(1:空 0:否)