数据结构与算法之栈与队列（上）

栈

相关定义

• 定义：它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。
• 栈顶：表尾称为栈顶
• 栈底：相对栈顶的另一端称为栈底
• 进栈出栈：向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

特点：先进后出，后进先出

栈的结构：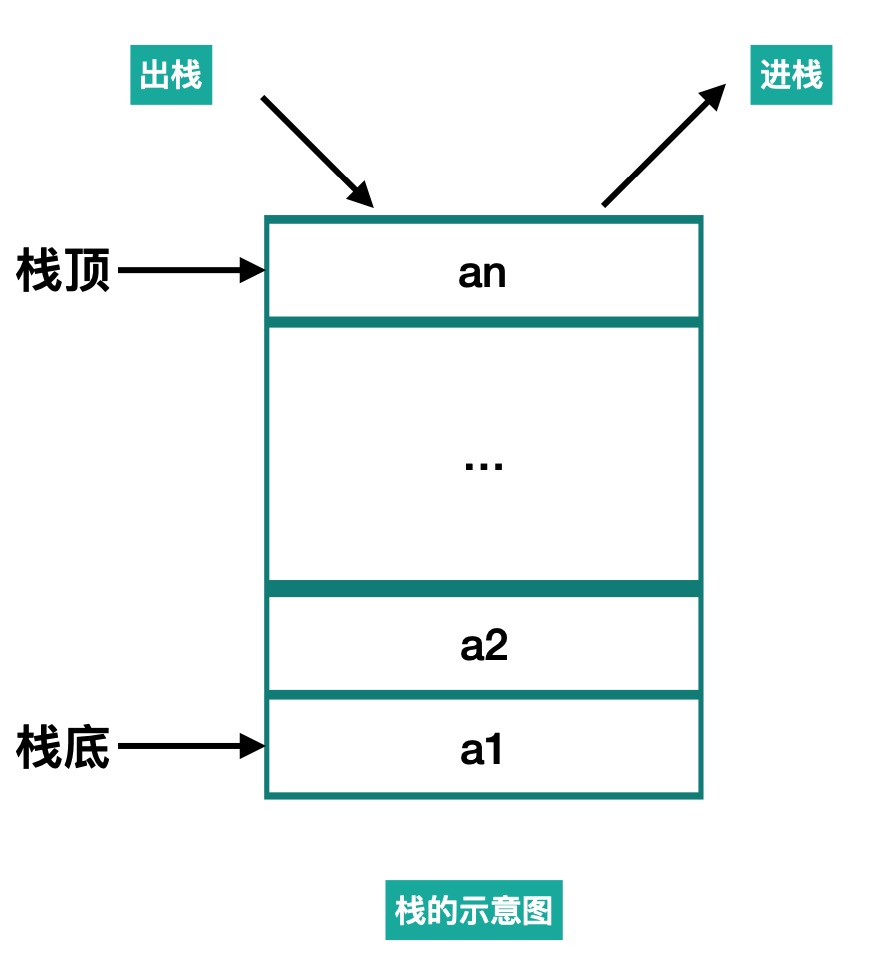

栈的代码实现

    顺序栈

• 顺序栈结构

typedef int Status;
typedef int SElemType; /* SElemType类型根据实际情况而定，这里假设为int */

/* 顺序栈结构 */
typedef struct
{
    SElemType data[MAXSIZE];
    int top; /* 用于栈顶指针 */
}SqStack;

• 构建空的顺序栈

  #pragma mark - 构建空的顺序栈
  Status InitSqStack(SqStack *S){
      //初始化默认栈顶的top = -1
      S->top = -1;
      return OK;
  }
  

• 清空顺序栈

  #pragma mark - 清空栈
  Status CleanSqStack(SqStack *stack){
      //栈顶top = -1即栈为空
      stack->top = -1;
      return OK;
  }
  
  

• 判断顺序是否为空

  #pragma mark - 判断栈是否为空
  bool EmptySqStack(SqStack *stack){
      if (stack->top == -1) {
          return true;
      }else{
          return false;
      }
  }
  
  

• 获得栈的长度

  #pragma mark - 获得栈的长度
  int GetSqStackLength(SqStack stack){
      return stack.top + 1;
  }
  
  

• 获得栈顶元素

  #pragma mark - 获得栈顶元素
  Status GetTopElemType(SqStack stack, SElemType *data){
      if (stack.top == -1) {
          return ERROR;
      }
      *data = stack.data[stack.top];
      return OK;
  }
  
  

• 入栈（压栈）

  #pragma mark - 入栈
  Status PushSqStack(SqStack *stack, SElemType data){
      if (stack->top == MAXSIZE - 1) {//栈满了
          return ERROR;
      }
      stack->top++;
      stack->data[stack->top] = data;
      return OK;
  }
  

• 出栈

  #pragma mark - 出栈
  Status PopSqStack(SqStack *stack, SElemType *data){
      if (stack->top == -1) {//空栈
          return ERROR;
      }
      *data = stack->data[stack->top];
      printf("出栈的元素是:%4d\n",*data);
      stack->top--;
      return OK;
  }
  
  

• 遍历栈

  #pragma mark - 遍历栈
  void TraversalSqStack(SqStack stack){
      if (stack.top != -1) {
          printf("栈的内容\n");
          int i = 0;
          while (i<=stack.top) {
              //从栈底开始遍历
              printf("%d\n",stack.data[i++]);
          }
      }
  }

栈与链表

• 链式栈的结构

/**
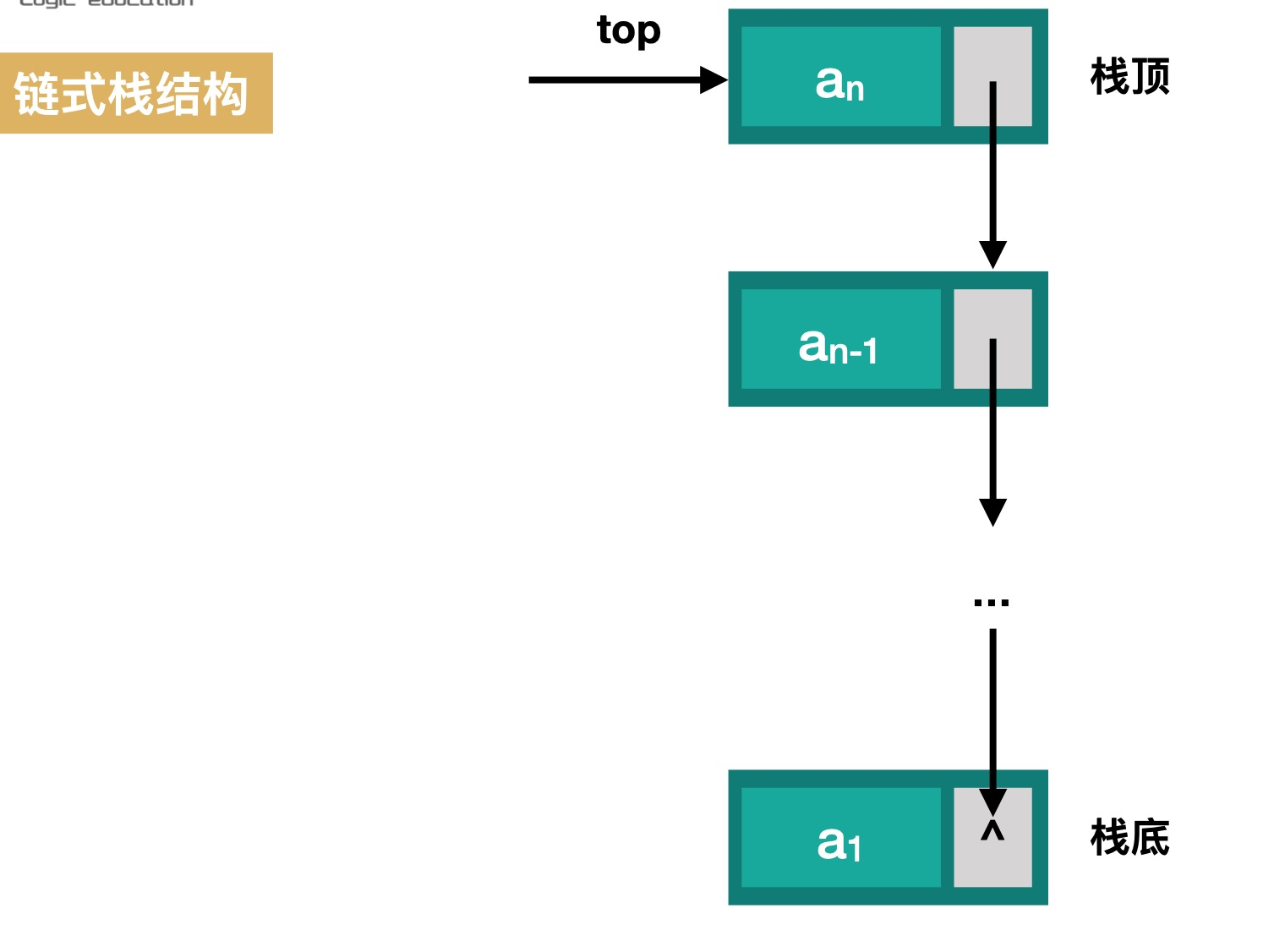
 栈结点
 */
typedef struct StackNode{
    SElemType data;
    struct StackNode *next;
}StackNode,*ModelStack;
/**
 链式栈的结构
 */
typedef struct {

    ModelStack top;
    //表示栈的长度
    int count;
}LinkStack;

• 初始化链式栈

  #pragma mark -初始化链式栈
  Status InitStackNode(LinkStack *stack){
      stack->top = NULL;
      stack->count = 0;
      return OK;
  }
  
  

• 链式栈清空

  #pragma mark - 将链式栈清空
  Status CleanStackNode(LinkStack *stack){
      ModelStack p,temp;
      //p指向栈顶
      p = stack->top;
      while (p) {
          temp = p;
          p = p->next;
          free(temp);
      }
      stack->top = NULL;
      stack->count = 0;
      return OK;
  }
  
  
  

• 是否是空的链式栈

  #pragma mark - 判断是否是空的链式栈
  bool EmptyStackNode(LinkStack stack){
      return stack.count == 0;
  }
  
  
  

• 获得链式栈的长度

  #pragma mark - 获得链式栈的长度
  int GetStackNodeLength(LinkStack stack){
      return stack.count;
  }
  
  

• 链式栈的入栈

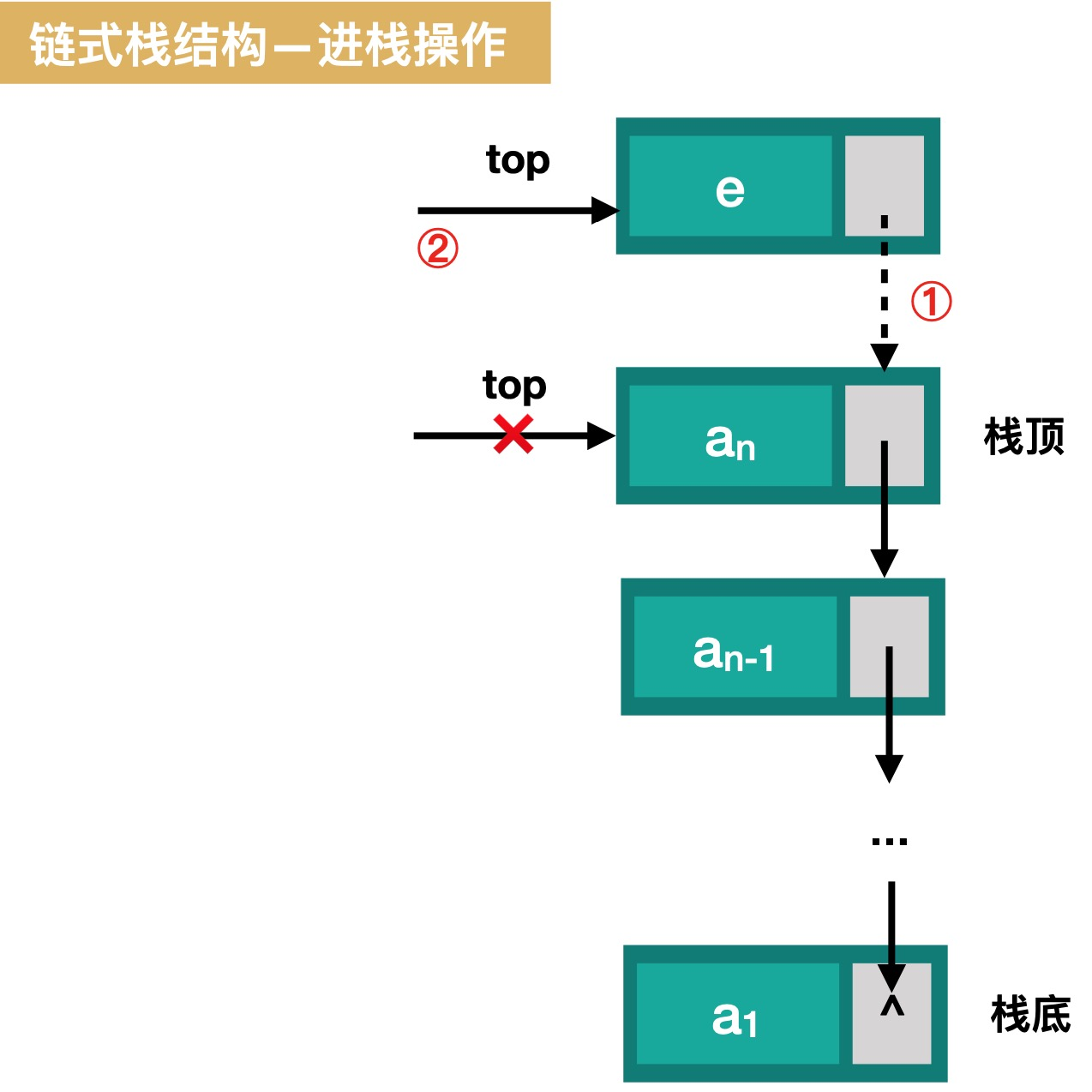
  #pragma mark - 入栈（压栈）
  Status PushStackNode(LinkStack *stack, SElemType data){
      if (!stack) {
          return ERROR;
      }
      ModelStack p = (ModelStack)malloc(sizeof(StackNode));
      //把当前的栈顶元素赋值给新结点的直接后继,stack->top是链式栈中前一个结点
      p->next = stack->top;
      p->data = data;
      //新的结点变成链式栈中的栈顶结点
      stack->top = p;
      
      stack->count++;
      return OK;
  }
  
  
  

• 链式栈的出栈

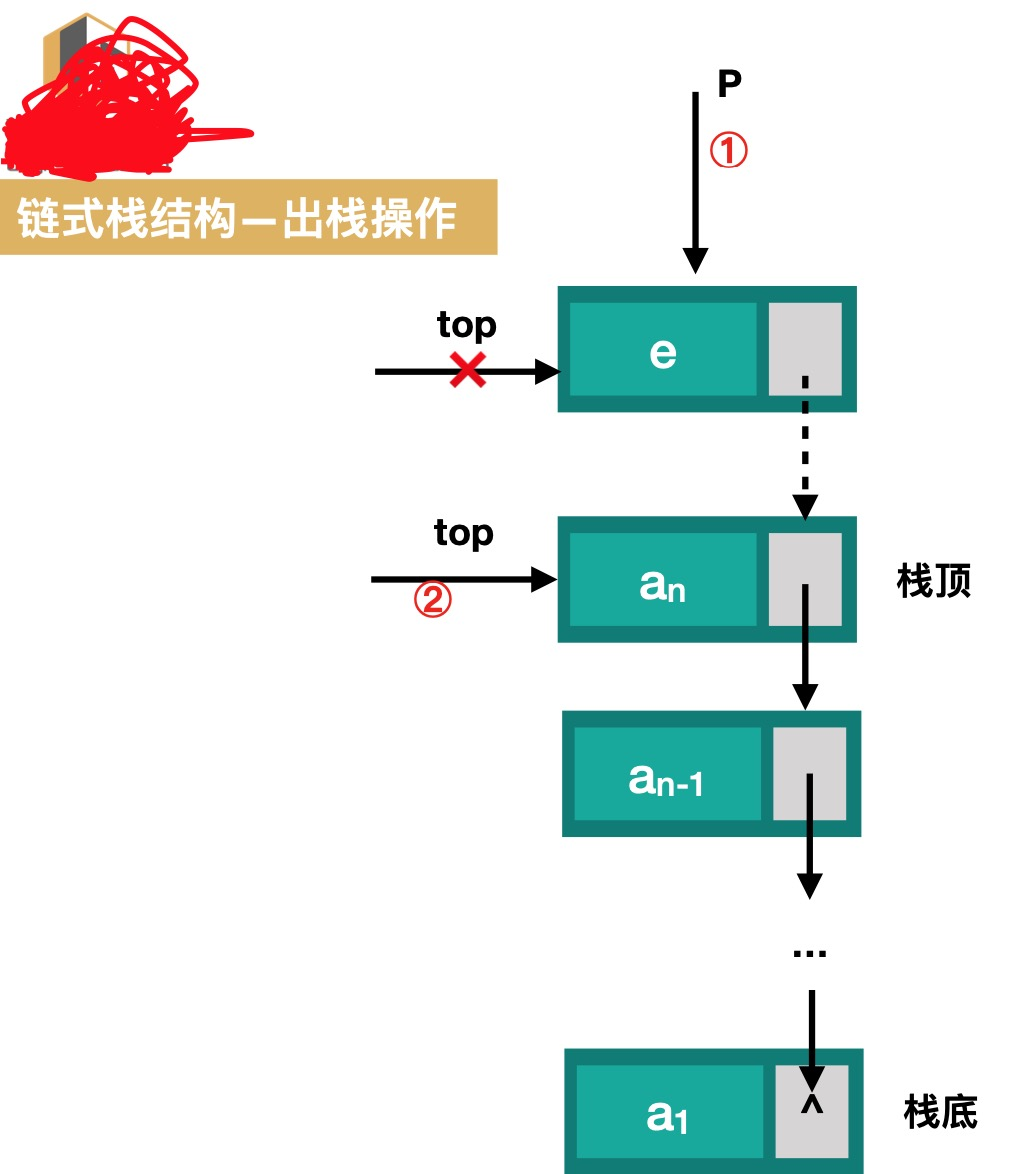
  #pragma mark - 出栈
  Status PopStackNode(LinkStack *stack, SElemType *data){
      if (!stack) {
          return ERROR;
      }
      ModelStack top = stack->top;
      *data = top->data;
      stack->top = top->next;
      free(top);
      stack->count--;
      return OK;
  }
  
  
  

• 链式栈的遍历

  #pragma mark - 遍历链式栈
  Status TraversalStackNode(LinkStack stack){
      if (stack.count == 0) {
          return ERROR;
      }
      ModelStack p = stack.top;
      printf("链式栈的内容：\n");
      while (p) {
          printf("%d\n",p->data);
          p = p->next;
      }
      return OK;
  }
  

栈与递归

   使用递归的情况

• 定义是递归的
• 数据结构是递归的
• 算法要求是递归的

两个函数之间如何调用的：在⾼级语⾔的程序中,调⽤函数和被调⽤的函数之间的链接与信息交换都是通过栈来进⾏的.通常,当在⼀个函数的运⾏期间调⽤另⼀个函数时, 在运⾏被调⽤函数之前, 系统需要先完成3件事情:

1. 将所有的实参,返回地址等信息调⽤传递被调⽤函数保存;

3. 将控制转移到被调函数⼊⼝;

⽽从被调⽤函数返回调⽤函数之前,系统同样需要完成3件事:

 兔子问题：如果兔⼦子2个⽉月之后就会有繁衍能⼒力力,那么⼀一对兔⼦子每个⽉月能⽣生出⼀一对兔⼦子; 假设所有的兔⼦子都不不死,那么n个⽉月后能⽣生成多少只兔⼦子?

/**
 如果兔⼦子2个⽉月之后就会有繁衍能⼒力力,那么⼀一对兔⼦子每个⽉月能⽣生出⼀一对兔⼦子; 假设所有的兔⼦子都不不死,那么n个⽉月后能⽣生成多少只兔⼦子?
思路：按月份计算，想算第n个月的兔子就需要先算n-1个月，想算n-1个月就要先算n-2个月的，依次类推直到第一个月位置，所以这是个递归
 复杂度：
        时间复杂度O(2^n),空间复杂度:O(1)
 */

long long getFbi(long n){
    if (n<2) {
        return n == 0 ? 0: 1;
    }
    return getFbi(n-1) + getFbi(n-2);
}

队列

相关定义

• 队列：它是一种操作受限的线性表，其限制在表的一端进行插入，另一端进行删除。
• 对尾、对头：可进行插入的一端称为队尾（rear）,可进行删除的一端称为队头（front）
• 入队、出队：向队中插入元素叫入队，新元素进入之后就称为新的队尾元素。从队中删除元素叫出队，元素出队后，其后继结点元素就称为新的队头元素。

特点：先进先出

几种队列图（本文是循环队列，链式队列在下一篇文章）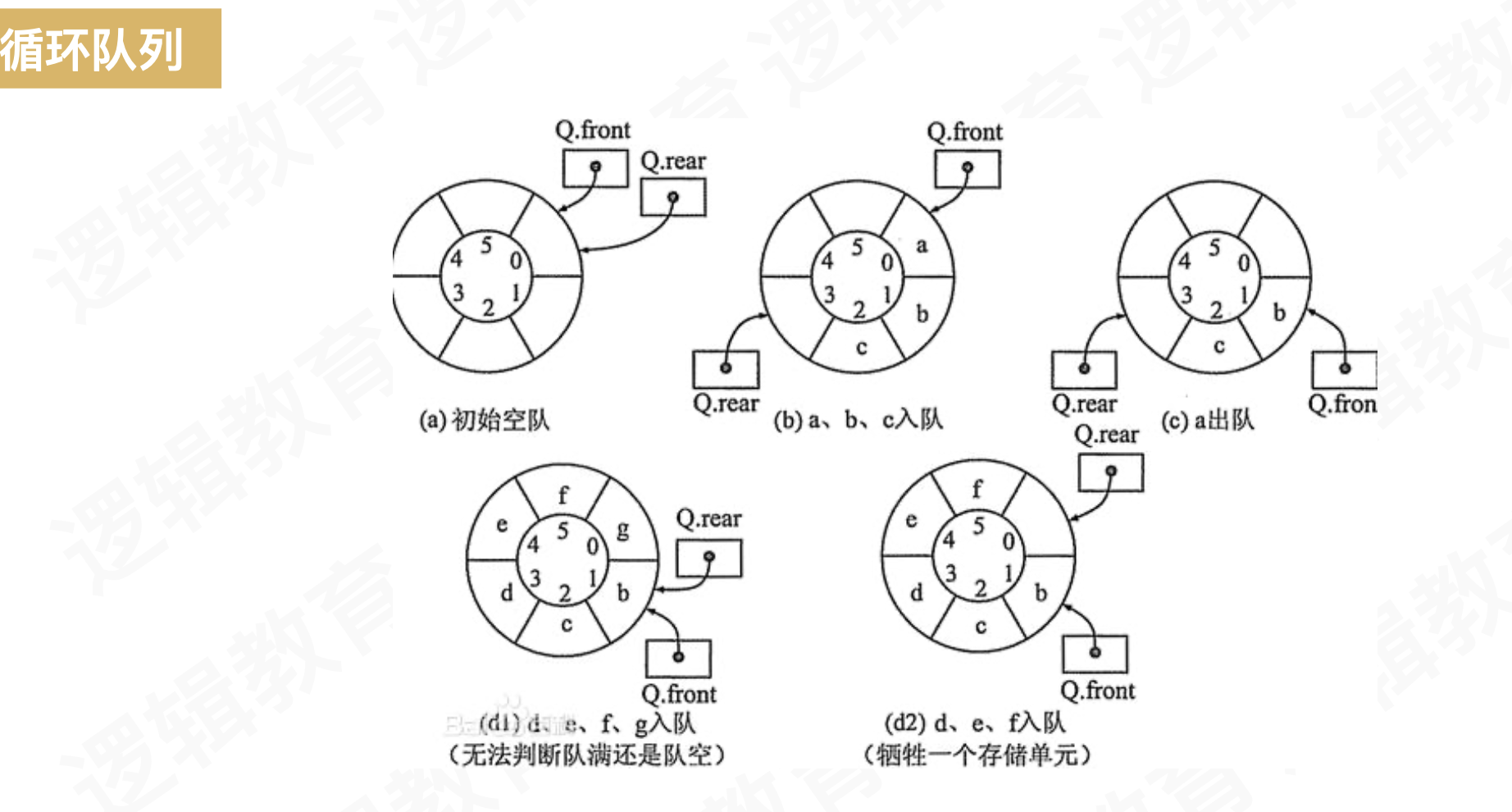

本文只对队列做简单介绍，下一篇文章将介绍队列

下一篇：数据结构与算法之栈与队列（下）