[翻书、走台阶问题]探索Fibonacii算法(JS实现)

引入

在算法题目中有翻书问题和走台阶的问题

• 共有n个台阶，每次只能上1个台阶或者2个台阶，共有多少种方法爬完台阶。
• 共有n页书，每次只能翻一页或者两页书，共有多少种方法翻完书。

以上两种场景，本质上都是斐波那契数列（Fibonacci sequence）

斐波那契数列,指的是这样一个数列：1、1、2、3、5、8、13、…… 斐波那契数列以如下被以递推的方法定义 F(1)=1，F(2)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 3，n ∈ N*）

我们从公式中，不难得出：

• F(1) = 1
• F(2) = 2
• F(n) = F(n-1) + F(n-2) (n>=3)

最简单的实现

function fibonacii(n){
    if(n === 1){
        return 1;
    }
    if(n === 2){
        return 2;
    }
    if(n > 2){
        return fibonacii(n-1) + fibonacii(n-2);
    }
}

export default fibonacii;

然后编写测试用例

import fibonacii from '../src/Fibonacci';

test('fibonacii:4',()=>{
    expect(fibonacii(4)).toEqual(5)
})

最后通过测试，耗时0.894s

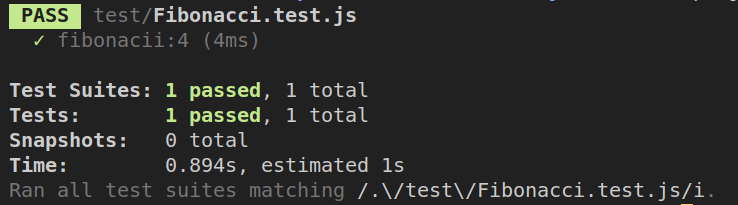
然后我们将输入进fibonacii()的值设为45;

会发现耗时11.45s

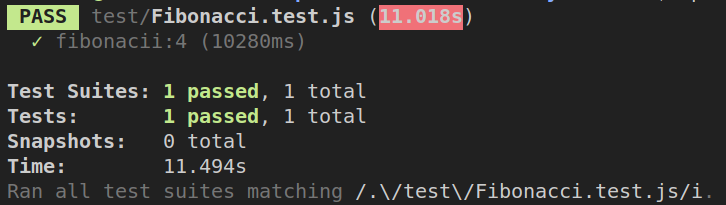
之后随着值变大，耗时也在成指数级别增长。

改进策略

因为F(50) = F(49) + F(48) = F(48) + F(47) + F(47) + F(46) = F(47) + (46) + F(46) + F(45) + F(46) + F(45) + F(45) + F(44) = ……

由此可得，F(47)此时已经算了3次，同理F(45)和F(46)也算了不只一次。

所以使用数组保存变量，用空间换取时间

function fibonacii(n){
    let res = new Array(n+1).fill(0);
    res[1] = 1;
    res[2] = 2;
    for(let i=3;i<n+1;i++){
        res[i] = res[i-1] + res[i-2];
    }
    return res[n]
}

编写同样的测试用例，计算第45位Fibonacii数

import fibonacii from '../src/Fibonacci';

test('fibonacii:4',()=>{
    expect(fibonacii(45)).toEqual(1836311903)
})

结果耗时

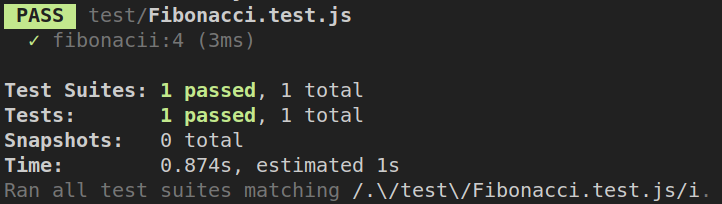
发现由之前的11.45秒到0.874秒 时间下降明显。

另一种方案

使用对象(字典)保存已经计算的变量，同样是空间换取时间

let cache = {};

function fibonacii(n){
   if (!(n in cache)){
    cache[n] =  _fibonacii(n);
   }

   return cache[n]
   
}
function _fibonacii(n){
    if(n === 1 || n === 2){
        return n;
    }else{
        return fibonacii(n-1) + fibonacii(n-2);
    }
}

同样计算45，结果为

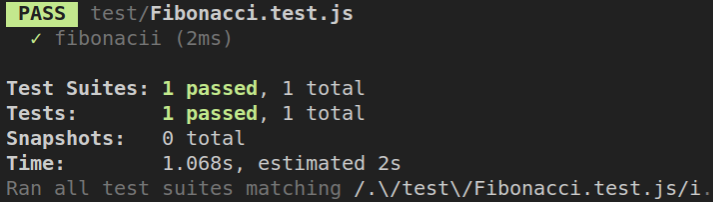
时间复杂度

在计算机科学中，时间复杂性，又称时间复杂度，算法的时间复杂度是一个函数，它定性描述该算法的运行时间。

使用O表示，是一种粗略的估计。

• N个数，F(N)
• 赋值：let a = 1; O(1)
• return 1; O(1)
• n === 2; O(1)
• O(1) 相对于 O(N)可以忽略
• O(N) 相对于 O(N^2)可以忽略
• O(N^2) 相对于 O(N^3)可以忽略

在下面这个算法中

function fibonacii(n){
    let res = new Array(n+1).fill(0);
    res[1] = 1; //O(1)
    res[2] = 2; //O(1)
    //循环为 O(n-2)
    for(let i=3;i<n+1;i++){
        res[i] = res[i-1] + res[i-2]; //赋值为O(1)
    }
    return res[n] //O(1)
}

所以这个算法的时间复杂度为:

O(1)+O(1)+O(n-2)*O(1) + O(1) = O(n+1)约等于O(n)

O(n)又叫线性时间复杂度

而在未被优化的算法中：

//假设时间复杂度为F(n);
//所以时间复杂度：F(n) = F(n-1) + F(n-2)
function fibonacii(n){
    if(n === 1){ // O(1)
        return 1; // O(1)
    }
    if(n === 2){ // O(1)
        return 2; // O(1)
    }
    if(n > 2){
        return fibonacii(n-1) + fibonacii(n-2); // F(n-1)+F(n-2)
    }
}

export default fibonacii;

而Fibonacii数列通项公式为(F(n)等于该通项公式)：

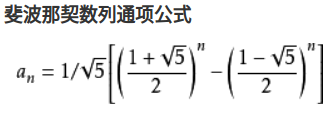
约等于2^n（指数级别）时间复杂度

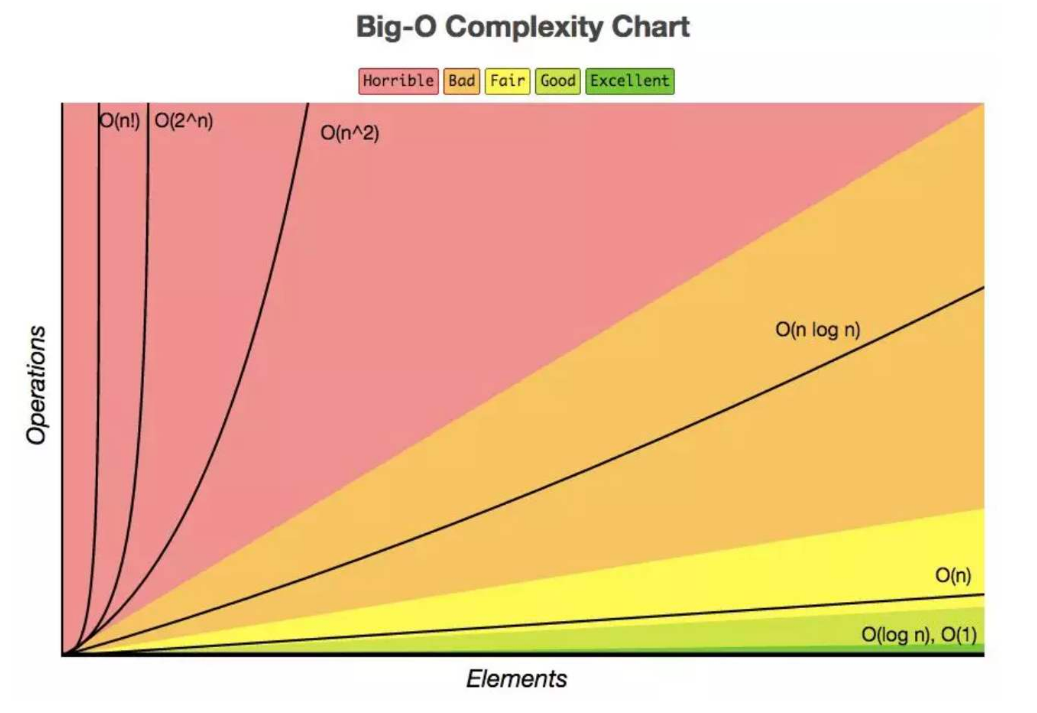
在下图可以得知，O(n)远远好于O(2^n)，所以后两个算法远远好于第一个算法。