数据结构-栈

先简单聊聊

之前学习的线性表以及线性表在物理结构中顺序存储和链式存储两种方式的代码实现。今天我们来学习一下一种特殊的线性表---栈，以及栈的顺序存储和链式存储。

1、栈是什么

栈是一种特殊的线性表，特殊点在于栈具有“先进后出”的一种形式。

1.1、何为“先进后出”

之前我们在学习线性表的时候，实现过相关的插入和删除方法。在线性表中，你可以在任意的位置插入和删除数据结点。而栈，只能在指定的位置插入和删除数据结点，我们通常叫这个指定位置为“栈顶”。对应的另一端，我们叫“栈底”。

概念比较简单，接下来我们直接上代码

2、相关代码

既然栈是线性表的一种，根据往期的学习，一下的代码要分为顺序存储和链式存储两种方式的实现

2.1、顺序存储

#include <stdio.h>
#include <stdlib.h>

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 20

typedef int Status;
typedef int SElemType;

typedef struct Stack{
    SElemType *data;
    int top;
}SqStack;

// init
Status initStack(SqStack *stack) {
    stack->data = (SElemType*)malloc(sizeof(SElemType) * MAXSIZE);
    stack->top = -1;
    return OK;
}

// clear
Status clearStack(SqStack *stack) {
    stack->top = -1;
    return OK;
}

// is empty
Status isEmptyStack(SqStack stack) {
    if (stack.top == -1) {
        return TRUE;
    } else {
        return FALSE;
    }
}

// stack长度
int length(SqStack stack) {
    return stack.top + 1;
}

//获取栈顶元素
Status getTopElem(SqStack stack, SElemType *elem) {
    if (stack.top == -1) {
        return ERROR;
    } else {
        *elem = stack.data[stack.top];
        return OK;
    }
}

// 入栈
Status pushElem2Stack(SqStack *stack, SElemType elem) {
    if (stack->top == MAXSIZE - 1) {
        return ERROR;
    }
    
    stack->top ++;
    stack->data[stack->top] = elem;
    return OK;
}

// 出栈
Status popElemFromStack(SqStack *stack, SElemType *elem) {
    if (stack->top == -1) {
        return ERROR;
    }
    
    *elem = stack->data[stack->top];
    stack->top--;
    return OK;
}

// 打印栈
Status displayStack(SqStack stack) {
    if (stack.top == -1) {
        return ERROR;
    }
    
    for (int i = 0; i <= stack.top; i++) {
        printf("%5d", stack.data[i]);
    }
    printf("\n");
    return OK;
}

2.2、链式存储

#include <stdio.h>
#include <stdlib.h>

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

typedef int Status;
typedef int ElemType;

typedef struct StackNode{
    ElemType data;
    struct StackNode *next;
    
}StackNode, *StackNodePtr;

typedef struct LinkStack{
    StackNodePtr top;
    int count;
}LinkStack;

//init
Status initStack(LinkStack *stack) {
    stack->top = NULL;
    stack->count = 0;
    return OK;
}

//clear
Status clearStack(LinkStack *stack) {
    StackNodePtr p = stack->top;
    StackNodePtr q;
    while (p) {
        q = p->next;
        free(p);
        p = q;
    }
    stack->top = NULL;
    stack->count = 0;
    
    return OK;
}

//isEmpty
Status isEmptyStack(LinkStack stack) {
    if (stack.count == 0) {
        return TRUE;
    } else {
        return FALSE;
    }
}

//length
int length(LinkStack stack) {
    return stack.count;
}

//getTopElem
Status getTopElem(LinkStack stack, ElemType *elem) {
    if (stack.top == NULL) {
        return ERROR;
    }
    *elem = stack.top->data;
    return OK;
}

//pushElem2Stack
Status pushElem2Stack(LinkStack *stack, ElemType elem) {
    StackNodePtr node = (StackNodePtr)malloc(sizeof(StackNode));
    if (node == NULL) {
        return ERROR;
    }
    node->data = elem;
    node->next = stack->top;
    stack->top = node;
    stack->count ++;
    return OK;
}

//popElemFromStack
Status popElemFromStack(LinkStack *stack, ElemType *elem) {
    if (stack->top == NULL) {
        return ERROR;
    }
    StackNodePtr p = stack->top;
    *elem = p->data;
    stack->top = stack->top->next;
    free(p);
    stack->count --;
    return OK;
}

//displayStack
Status displayStack(LinkStack stack) {
    StackNodePtr p = stack.top;
    while (p) {
        printf("%5d", p->data);
        p = p->next;
    }
    printf("\n");
    return OK;
}

3、栈的应用

在我们平时开发中，很少直接使用栈。但是栈又是相对比较基础的数据结构。

很多时候系统会给我们封装提供以栈的方式实现的模块，例如iOS中的UINavigationViewController，可能一些非客户端app的开发者不知道这个东西。它就是从一个界面中，点击一个按钮，进入到另一个界面，相当于栈的入栈；当你点击返回的时候，回到前一个界面，相当于出栈。

其实，还有一个我们更常用的，而且每个人都会用的，但平时不会太多去注意到的一个点，就是函数调用。在高级语言的程序中，调用函数和被调用函数之间的链接和信息交换都是通过栈的形式来实现的。

3.1、函数调用

在一个函数（以下用“调用函数”表示）内，调用另一个函数（以下用“被调用函数”表示），在运行被调用函数之前，系统会先完成下面的几件事

• 将实参、返回地址等相关信息传递给被调用函数中保存
• 为被调用函数的局部变量分配存储空间
• 将控制转移到被调用函数的入口

从被调用函数返回到调用函数之前，系统同样会做一些事情

• 保存被调用函数的结果
• 释放被调用函数的数据区
• 根据被调用函数保留的返回地址，将控制权转移回调用函数中。

当多个函数构成嵌套条用时，按照“先调用后返回”方式，也就是先进后出的栈的形式实现的。

比如代码实现：

int second(int d){ 
int x,y;
//...
}
int first(int s ,int t){ 
int i;
//... 
second(i)//2.⼊入栈 
//...
}
void main( ){ 
int m,n;
first(m ,n); //1.⼊入栈
//...
}

当main函数中，调用了first函数，main函数就是调用函数，first函数就是被调用函数。方法调用的栈结构如图：

first函数中又调用了second函数，如图：

函数调用时，栈空间中保存了方法名，参数，和相关临时变量。

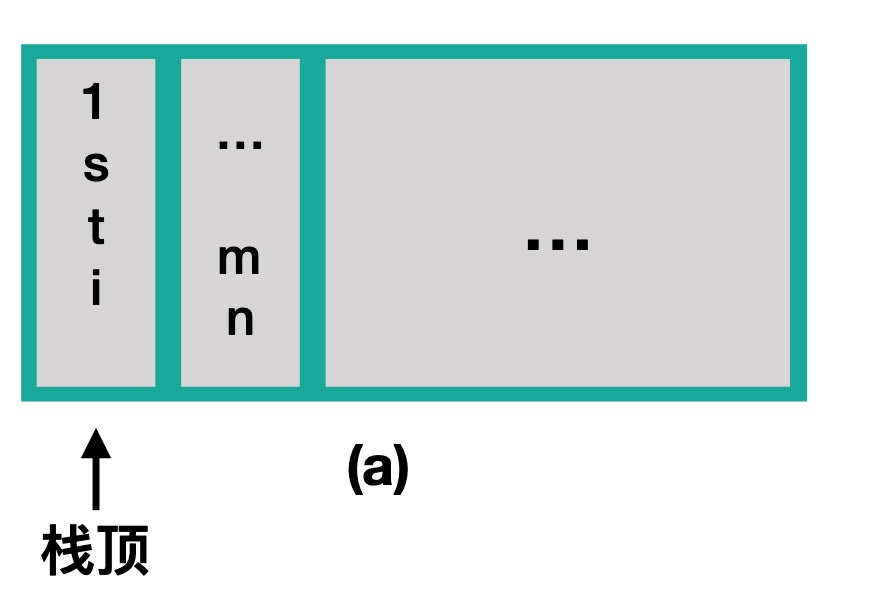
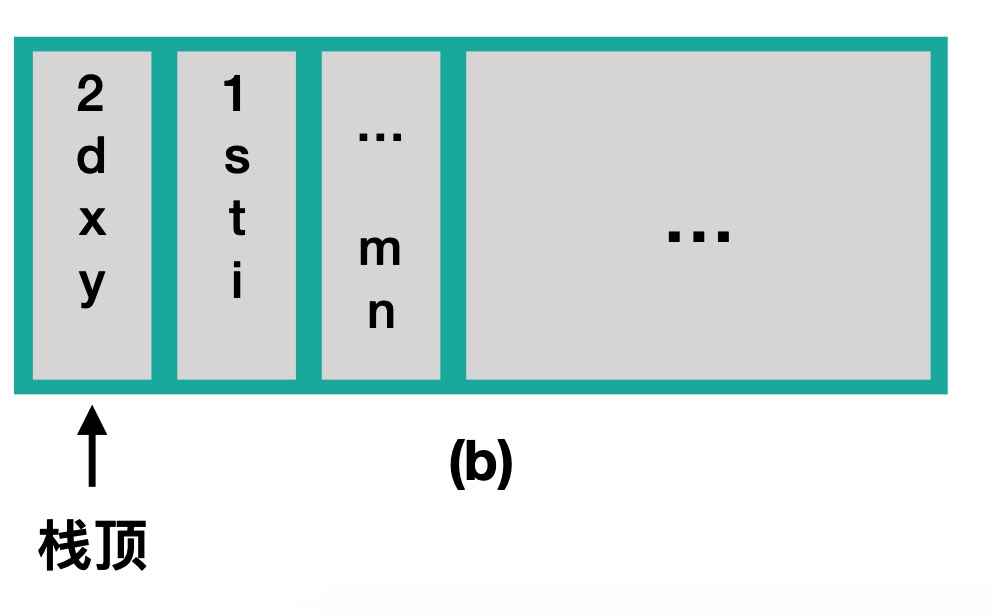
3.2、递归函数

递归函数运行过程类似多个函数嵌套调用，只是调用函数和被调用函数是同一个函数。

为了保证递归函数的正确调用，系统需要设立一个“递归工作栈”作为整个递归函数运行期间的数据存储区。每一层递归所需信息构成一个工作记录，其中包括所有的实参，所有的局部变量以及上一层的返回地址。每进入一层递归，就产生一个新的工作记录压入栈顶。没退出一个递归，就从栈顶弹出一个记录。

扩展内容

什么是递归？

在一个函数，过程或数据结构敌营的内部又直接或间接出现定义本身的应用；则称为他们是递归的或者是递归定义。

在下面3中情况下，我们会使用到递归来解决问题

1. 定义是递归的

阶乘

// Fact(n)
// 若n=0, 则返回1;
// 若n > 1, 则返回n*Fact(n-1);
 long Fact(Long n){
 if(n=0) return -1;
 else return n * Fact(n-1);
}

斐波拉契数列

//Fib(n)
// 若n=1或者n=2,则返回1;
// 若n > 2, 则Fib(n-1) + Fib(n-2);
long Fib(Long n){
    if(n == 1 || n == 2) return 1;
    else return Fib(n-1)+Fib(n-2);
}

2. 数据是递归的 之前我们学习过的链表，就是一种数据递归。链表结点中包含data和next指针，next指向的是链表结点的类型。遍历链表时可以使用递归的方式

void TraverseList(LinkList p){
    if(p == NULL) return; 
    else{
        printf("%d",p->data); 
        p TraverseList(p->next);
    }
}

3. 问题的解法是递归的

有一类问题，虽然问题本身并没有明显的递归结构，但是采取递归求解比迭代更简单，如Hanoi塔问题、八皇后问题、迷宫问题

//汉诺塔 Hanoi
void Hanoi(int n, char a, char b, char c) {
    if (n == 1) {
        moves(a, 1, c);
    } else {
        Hanoi(n-1, a, c, b);
        moves(a, n, c);
        Hanoi(n-1, b, a, c);
    }
}

int main(int argc, const char * argv[]) {
    // insert code here...
    printf("Hello, Hanoi!\n");
    Hanoi(4, 'a', 'b', 'c');
    return 0;
}

使用递归的条件

• 能讲问题转变成小问题，而小问题和原问题解法相同或类同，不同的仅仅是处理的对象数据，并且这些处理更小且变化有规律
• 可以通过转换而使得问题简化
• 必须有一个明确的递归出口或称为递归边界值。

总结

这节课的学习是在原有的基础上扩展出来的，但是注意到了平时不注意的点（函数调用是栈的逻辑）。希望以上的总结，可以给你带来帮组。记住：沿途的风景要比目的地更弯的否！！！