查找算法1. 顺序查找 2. 二分查找将数列按有序化(递增或递减)排列，查找过程中采用跳跃式方式查找，即先以有序数列的

1. 顺序查找

2. 二分查找

将数列按有序化(递增或递减)排列，查找过程中采用跳跃式方式查找，即先以有序数列的中点位置为比较对象，如果要找的元素值小于该中点元素，则将待查序列缩小为左半部分，否则为右半部分。通过一次比较，将查找区间缩小一半。折半查找是一种高效的查找方法。它可以明显减少比较次数，提高查找效率。但是，折半查找的先决条件是查找表中的数据元素必须有序。

3. 插值查找

插值查找（Interpolation Search）是根据要查找关键字key与查找表中最大最小记录的关键字比较后的查找方法，其核心就在于插值的计算公式key-arr[low]/arr[high]-arr[low]。细看是不是key在整序列中的占比哟。所以mid的计算公式为：

（high-low）*（key-arr[low]）/（arr[high]-arr[low]）。对比折半查找的mid = （high-low）/2。

代码和折半查找一模一样，唯独mid的计算方式发生改变。这样的好处在于，对表长较长，且关键字分分布比较均匀，插值查找算法的平均性能要比折半查找要好的多。但是如果表中关键字分布极端不均匀那么插值查找还不如折半查找呢。

package cn.dzp.flyroc.search;

public class InterSearchDemo {

    public static void main(String[] args){
        int[] arr ={1,3,6,8,32,56,59,67,76,86,95,99,200,298,299,300,309,345,356,387,293,399,400,490,500};
        interSearch(arr, 6);


    }

    //插值查找
    public static void interSearch(int[] arr, int key){
        int low = 0;        
        int high = arr.length-1;

        int mid;        //定义中间值

        while (low <= high){

            mid = low + (key - arr[low])/(arr[high]-arr[low])*(high-low);       //中间值
            if (arr[mid] == key){       //如果找到
                System.out.println("这个元素的索引是："+mid);
                return ;
            }else if(arr[mid] < key){       //中间值小
                low = mid +1;
            }else {     //中间值大
                high = mid -1;

            }
        }
    }
}

4. 斐波那契查找

斐波那契查找就是在二分查找的基础上根据斐波那契数列分割的，在斐波那契数列找一个等于略大于待查找表长度的数f(k),待查找表长度扩展为f(k)-1(如果原来数组长度不够f(k)-1，则需要扩展，扩展时候用原待查找表最后一项填充),mid = low + f(k-1) -1,已mid为划分点，将待查找表划分为左边，右边

划分图示

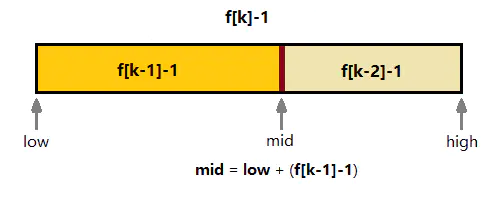
划分原因

斐波那契数列 f(k) = f(k - 1) + f(k -2)

假如待查找数组长度为f(k),不考虑mid的情况下，左边为f(k - 1),右边为f(k-2),考虑mid的情况下要不左边是f(k-1) - 1或者右边是f(k - 2) - 1，逻辑不好写

如果待查找长度为f(k) - 1，mid = low + (f(k - 1) - 1)则不存在这样的问题

为什么待查找长度不为f(k-1) - 1，不为f(k+1) - 1?感兴趣的自己去论证

#include <stdio.h>
#include <cstring>

int size = 20;
void fibonacci (int *f) {
    f[0] = 1;
    f[1] = 1;
    for (int i = 2; i < size; i++) {
        f[i] = f[i-1] + f[i-2];
    }
}

int fibonacciSearch (int *a, int n, int key) {
    int f[size];
    fibonacci(f);
    
    //找到略大于n的f(k)
    int index = -1;
    for (int k = 0; k<size; k++) {
        if (f[k] > n) {
            index = k;
            break;
        }
    }
    
    //填充数组长度为tmp - 1;
    int *temp;//将数组a扩展到F[k]-1的长度
    temp = new int [f[index] - 1];
    memcpy(temp,a,n*sizeof(int));
    
    int i = n;
    while (i < f[index] - 1) {
        temp[i] = a[n - 1];
        i++;
    }
    
    int low =0,high = f[index] - 2;
    while (low <= high) {
        int mid = low + f[index - 1] - 1;
        if (temp[mid] == key) {
            if (mid < n) {
                return mid;
            } else {
                return n-1;
            }
        } else if (temp[mid] > key) {
            high = mid - 1;
            index = index - 1;
        } else {
            low = mid + 1;
            index = index - 2;
        }
    }
    
    return -1;
}

int main(int argc, const char * argv[]) {
    int a[] = {0,16,24,35,47,59,62,73,88,99};
    int key=99;
    int index=fibonacciSearch(a,sizeof(a)/sizeof(int),key);
    printf("locate at %d\n",index);
    return 0;
}

5. 树表查找

6. 分块查找

分块查找又称索引顺序查找，它是顺序查找的一种改进方法。

算法流程：

先选取各块中的最大关键字构成一个索引表；
查找分两个部分：先对索引表进行二分查找或顺序查找，以确定待查记录在哪一块中；然后，在已确定的块中用顺序法进行查找。

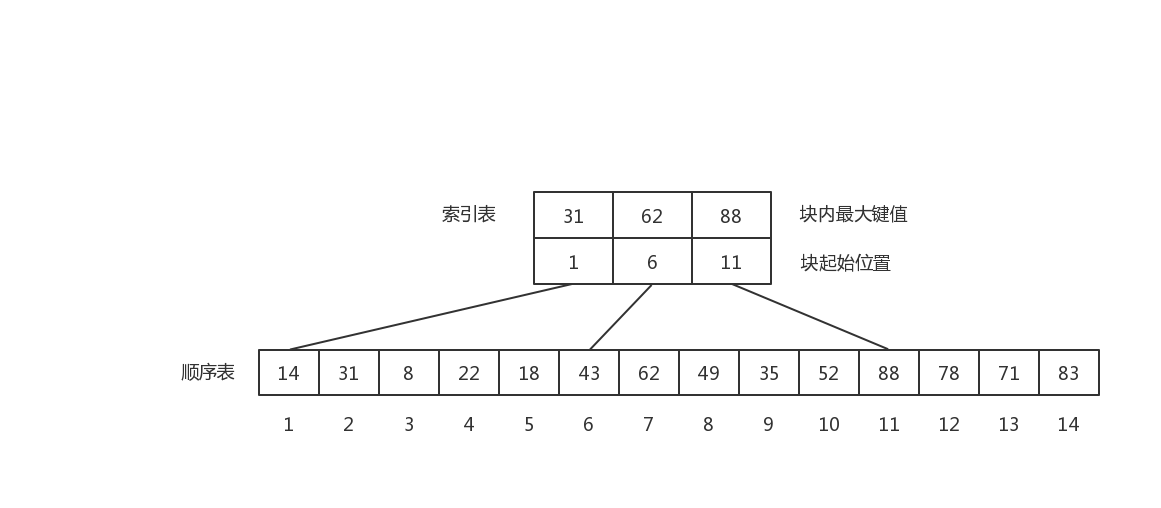
注：算法的思想是将n个数据元素"按块有序"划分为m块（m ≤ n）。每一块中的结点不必有序，但块与块之间必须"按块有序"，每个块内的的最大元素小于下一块所有元素的任意一个值。

所以，给定一个待查找的key，在查找这个key值位置时，会先去索引表中利用顺序查找或者二分查找来找出这个key所在块的索引开始位置，然后再根据所在块的索引开始位置开始查找这个key所在的具体位置。

查找算法