在上一节中，我们介绍了非重叠社区发现问题中基于标签传播的算法。而非重叠社区另一种经典的做法就是基于模块度的社区发现算法。接下来，我们将首先介绍模块度的概念，为基于模块度的社区发现算法打好基础。

模块度

我们可以发现，在LPA算法中，没有指标能够衡量当前社区划分的好坏，仅仅是根据一定的更新原则更新到网络收敛为止。由于其随机性强，很容易出现执行多次的结果各不相同，难以收敛稳定。
为了评价社区划分的优劣，Newman等人提出了模块度的概念，用模块度来衡量社区划分的好坏。一个相对好的结果，就是社区内部节点连接更为稠密，社区间连接更为稀疏，此时的模块度会更大。这样就将社区发现问题转换为最大化网络模块度问题。

模块度公式

模块度第一版定义

根据上面描述的情况，如何定义社区内部节点连接更为稠密呢？
Newman给出了如下的概念：假设网络被划分成 $k$ 个社区，那么定义一个 $k \times k$ 的对称矩阵 $e$ ，其中元素 $e_{ij}$ 就表示社区 $i$ 和社区 $j$ 的连边数， $e_{ii}$ 表示的就是社区i内部的连边数。那么我们可以发现，矩阵 $e$ 的迹 $Tr(e)=\sum_i e_{ii}$ 表示的就是相同社区内边的集合。那么很明显， $Tr(e)$ 越大，越能表示社区内部链接越稠密，说明社区划分的结果越合理。但是存在这么一个问题，就是无法展现出社区间连接更为稀疏。如果整个网络划分到一个社区中，此时的 $Tr(e)$ 应该是最大的。
因此Newman又定义了一个行（或列）的和 $a_i = \sum_j e_ {ij}$ ，表示与社区i相连的所有边。
此时可以定义出第一版模块度的公式：

Q = \sum_i(e_{ii}-a_i^2) = \sum_i(e_{ii}) - \sum_i(a_i^2) = Tr(e) - ||e^2||

根据定义我们可以发现，模块度其实就是对网络的所有社区做一个累加操作，用社区内的边度数减去社区内节点的度数。直观上，如果社区的节点都只内部相连，这个值会较大。如果社区内的节点还和外面的节点有较多链接，这个值就会较小。
我们用以下一个例子进行说明。网络总共包含6个节点：a，b，c，d，e，f，存在下述4种社区划分结果，其中社区编号分别为1，2，3，4，5，6。

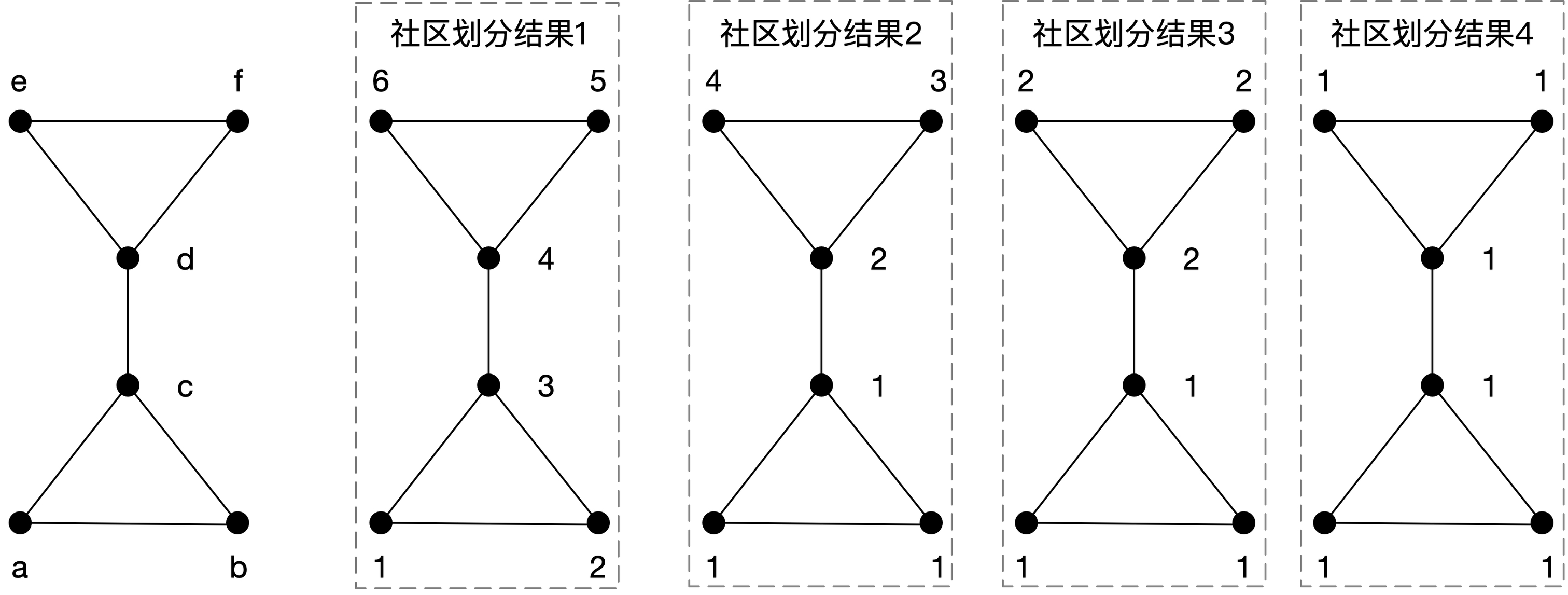
以第二种社区划分结果为例，我们可以写出它的社区矩阵：

e_2 = \left[
\begin{matrix}
2*3 & 1 & 0 & 0 \\
1 & 2*0 & 1 & 1 \\
0 & 1 & 2*0 & 1 \\
0 & 1 & 1 & 2*0
\end{matrix}
\right] = \left[
\begin{matrix}
6 & 1 & 0 & 0 \\
1 & 0 & 1 & 1 \\
0 & 1 & 0 & 1 \\
0 & 1 & 1 & 0
\end{matrix}
\right]

这里要注意，计算社区内部节点的时候，每条边要算两次。算两次的原因在于我们在计算社区间的边，实际上也是算了两遍（比如节点c,d这条边，属于社区 $1$ 和社区 $2$ ，那么其实 $e_{21}$ 和 $e_{12}$ 都算了1）。
还有一点值得注意，为了保证结果的可度量性，我们在计算时需要根据总边数（这个边数也要算两次，这个例子中总边数就是 $2\times7=14$ ）进行归一化。根据上述的公式，我们可以计算模块度 $Q$ ：

Q_2=\frac{6}{14}-(\frac{7}{14})^2-(\frac{3}{14})^2-(\frac{2}{14})^2-(\frac{2}{14})^2 \approx 0.092

同理，我们可以列出其他三种社区划分结果的矩阵并计算想要的模块度Q。
社区划分结果 $1$ 中，共有6个社区，得到：

e_1 = \left[
\begin{matrix}
0 & 1 & 1 & 0 & 0 & 0 \\
1 & 0 & 1 & 0 & 0 & 0 \\
1 & 1 & 0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 & 1 & 1 \\
0 & 0 & 0 & 1 & 0 & 1 \\
0 & 0 & 0 & 1 & 1 & 0 \\
\end{matrix}
\right]

Q_1=0-(\frac{2}{14})^2-(\frac{2}{14})^2-(\frac{3}{14})^2-(\frac{3}{14})^2-(\frac{2}{14})^2-(\frac{2}{14})^2 = -0.236

社区划分结果 $3$ 中，共有2个社区，得到：

e_3 = \left[
\begin{matrix}
6 & 1 \\
1 & 6 \\
\end{matrix}
\right]

Q_3= \frac{12}{14} - (\frac{7}{14})^2 - (\frac{7}{14})^2= 0.357

社区划分结果 $4$ 中，共有1个社区，得到：

e_4 = \left[
\begin{matrix}
14 \\
\end{matrix}
\right]

Q_4= \frac{14}{14} - (\frac{14}{14})^2 = 0

第一版定义详情可以见于论文Finding and evaluating community structure in networks的第四部分。

模块度第二版定义

第二版的模块度定义为：社区内边数的比例（社区边数/网络总边数）-社区内节点产生边数的期望（随机网络下同样的社区的期望边数）。具体的公式如下：

Q=\frac{1}{2m}\sum_{vw}\left[A_{vw}-\frac{k_vk_w}{2m}\right]\delta(c_v,c_w)

其中 $A_{vw}$ 表示该网络的邻接矩阵的元素。也就是：

A_{vw}=
\begin{cases}
1, & 节点v和节点w相连 \\
0, & otherwise
\end{cases}

$c_v$ 表示节点 $v$ 所属的社区。函数 $\delta(c_v,c_w)$ 表示两个社区是否相同，也就是：

\delta(c_v,c_w)=
\begin{cases}
1, & c_v = c_w \\
0, & otherwise
\end{cases}

根据这两个定义，我们就可以计算社区内边数的比例（社区边数/网络总边数）。
社区边数之和为 $\sum_{vw}A_{vw}\delta(c_v,c_w)$ ,网络总边数为 $\sum_{vw}A_{vw}$ 。
此时要注意，由于 $v$ 和 $w$ 可互换，相当于网络中每条边计算了2次。所以我们定义网络的实际边数 $m=\frac{1}{2}\sum_{vw}A_{vw}$ 。
同时，根据邻接矩阵的性质，我们也可以计算出一个节点的度数 $k_v = \sum_wA_{vw}$ 。
我们已经能够计算社区内边数的比例，接下来就是计算随机网络下同样的社区的期望边数。我们不妨这么考虑，无论随机网络是什么样子，整体的网络结构是不能变化的，也就是这个网络的边仍然是 $m$ 条（如果和版本一那样考虑，就是 $2m$ 条）。而每个节点的度数也是不能变化的（变化的话就不是同一个网络了）。我们以“版本一”的定义来考虑，对于 $v$ 和 $w$ 构成的边 $e_{vw}$ ，假定 $v$ 是起点， $w$ 是终点，那么 $e_{vw}$ 就存在 $k_wk_v$ 种边的组合，而总的边数只有 $2m$ 条，所以期望就是 $\frac{k_vk_w}{2m}$ （期望边数不一定是整数）。
至此，我们就完成了模块度的定义。我们可以对模块度的定义进行进一步的计算：

\begin{eqnarray}
Q &=& \frac{1}{2m}\sum_{vw}\left[A_{vw}-\frac{k_vk_w}{2m}\right]\delta(c_v,c_w)\\
&=& \frac{1}{2m}\left[ \sum_{vw}A_{vw}-\frac{\sum_vk_v\sum_wk_w}{2m}\right]\delta(c_v,c_w) \\
&=& \frac{\sum_{vw}A_{vw}\delta(c_w,c_v)}{2m} - \frac{\sum_vk_v\sum_wk_w\delta(c_w,c_v)}{(2m)^2} \\
&=& \sum_i[\frac{in}{2m} - (\frac{tot}{2m})^2]\\
&=& \sum_i(e_{ii}-a_i^2)
\end{eqnarray}

惊喜的是，虽然初始的定义不同，但是通过推导，我们发现版本一和版本二的结果完全一致。仔细一想，我们可以发现社区内的边数之和其实就是社区矩阵 $e$ 的迹 $Tr(e)$ ，而随机网络下的同社区中总的期望边数也等价于该社区内的总度数的平方（为保证网络结构稳定，节点的度数必须要有边承载，而一条边必须要承接两个节点的度数，所以是平方）。

第二版定义详情可以见于论文Finding community structure in very large networks的第二部分。