经典排序算法共有十种,在这里我就介绍下我学习的的五种排序算法:选择排序(Selection Sort)、快速排序(Quick Sort)、归并排序(Merge Sort)、计数排序(Counting Sort)和冒泡排序(Bubble Sort)
1.选择排序(Selection Sort)
选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
代码实现:
//选择排序(用for循环)
let sort = (numbers) => {
for (let i = 0; i < numbers.length - 1; i++) {
console.log(`----`);
let index = minIndex(numbers.slice(i)) + i;
console.log(`index:${index}`);
if (index !== i) {
console.log(`i:${i}`);
swap(numbers, index, i);
console.log(`swap ${index}:${i}`);
}
}
return numbers;
};
let swap = (array, a, b) => { //函数交换数组两个元素
let temp = array[a];
array[a] = array[b];
array[b] = temp;
};
let minIndex = (numbers) => numbers.indexOf(min(numbers));
let min = (numbers) => { //函数取最小值
if (numbers.length > 2) {
return min([numbers[0], min(numbers.slice(1))]);
} else {
return Math.min.apply(null, numbers);
}
};
sort([5, 2, 8, 9, 24, 15, 36]); //[2,5,8,9,15,24,36]动画演示:
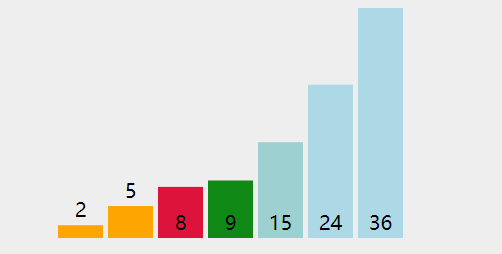
算法分析:
表现最稳定的排序算法之一,因为无论什么数据进去都是O(n2)的时间复杂度,所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。理论上讲,选择排序可能也是平时排序一般人想到的最多的排序方法了吧。
2.快速排序(Quick Sort)
快速排序(Quick Sort)的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
代码实现:
//快速排序
let quickSort = (arr) => {
if (arr.length < 2) {
return arr;
}
let pivotIndex = Math.floor(arr.length / 2); //把数组分成两部分
let pivot = arr.splice(pivotIndex, 1)[0]; //pivot为基准
let left = [];
let right = [];
for (let i = 0; i < arr.length; i++) {
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat([pivot], quickSort(right));
};
quickSort([8, 6, 4, 2, 48, 26, 39]); //[2,4,6,8,26,39,48]
动画演示:
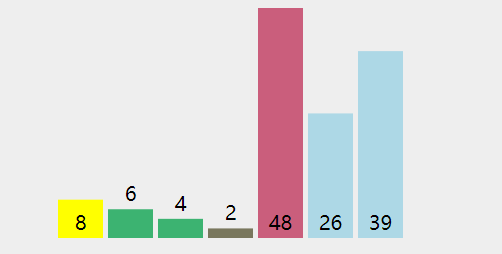
算法分析:
快速排序是一种稳定的排序方法。和选择排序一样,快速排序表现比选择排序快得多,因为是O(nlogn)的时间复杂度。代价是需要额外的内存空间。
3.归并排序(Merge Sort)
归并排序(Merge Sort)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
代码实现
//归并排序
let mergeSort = (arr) => {
let a = arr.length;
if (a === 1) {
return arr;
}
let left = arr.slice(0, Math.floor(a / 2));
let right = arr.slice(Math.floor(a / 2));
return merge(mergeSort(left), mergeSort(right));
};
let merge = (a, b) => { //比较合并
if (a.length === 0) {
return b;
}
if (b.length === 0) {
return a;
} else {
return a[0] > b[0]
? [b[0]].concat(merge(a, b.slice(1)))
: [a[0]].concat(merge(a.slice(1), b));
}
};
mergeSort([8,5,2,7,15,52,37])//[2,5,7,8,15,37,52]动画演示:
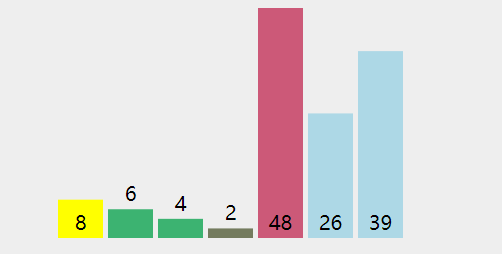
算法分析:
归并排序是一种稳定的排序方法。和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是O(nlogn)的时间复杂度。代价是需要额外的内存空间。
4.计数排序(Counting Sort)
计数排序(Counting Sort)不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
代码实现:
//计数排序;
let countSort = (arr) => {
let hashTable = {},
max = 0,
result = [];
for (let i = 0; i < arr.length; i++) { //遍历整个数组
if (!(arr[i] in hashTable)) {
hashTable[arr[i]] = 1;
} else {
hashTable[arr[i]] += 1;
}
if (arr[i] > max) {
max = arr[i];
}
}
for (let j = 0; j <= max; j++) {
if (j in hashTable) {
for (let a = 0; a < hashTable[j]; a++) {
result.push(j);
}
}
}
return result;
};
countSort([5,5,4,9,4,2,7,4,7,3,8,1,6,3,5])//[1,2,3,3,4,4,4,5,5,5,6,7,7,8,9]动画演示:
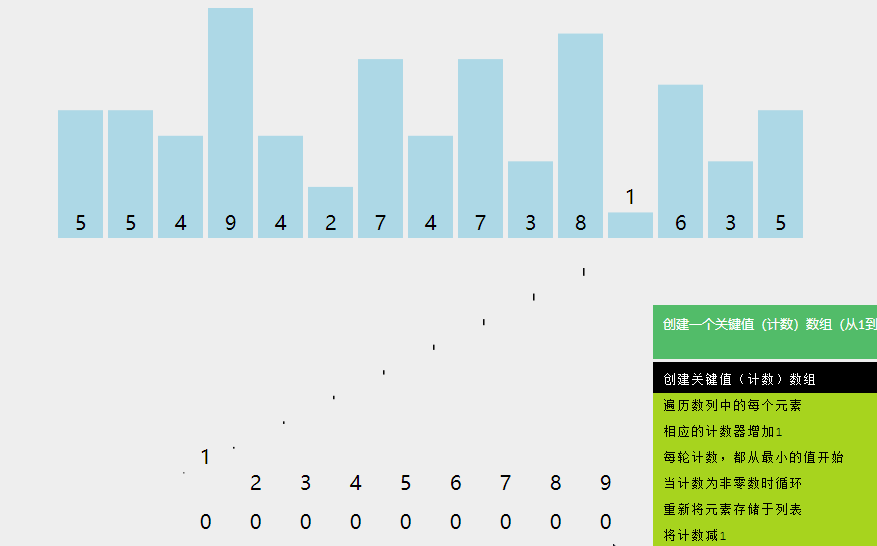
算法分析:
计数排序是一个稳定的排序算法。当输入的元素是 n 个 0到 k 之间的整数时,时间复杂度是O(n+k),空间复杂度也是O(n+k),其排序速度快于任何比较排序算法。当k不是很大并且序列比较集中时,计数排序是一个很有效的排序算法。
5.冒泡排序(Bubble Sort)
冒泡排序(Bubble Sort)是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
代码实现:
//冒泡排序
function bubbleSort(arr) {
var len = arr.length;
for (var i = 0; i < len - 1; i++) {
for (var j = 0; j < len - 1 - i; j++) {
if (arr[j] > arr[j+1]) { // 相邻元素两两对比
var temp = arr[j+1]; // 元素交换
arr[j+1] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
bubbleSort([8,5,2,7,15,49,37]) //[2,5,7,8,15,37,49]动画演示:
算法分析:
冒泡排序是一种稳定的排序方法。和选择排序一样,冒泡排序的性能不受输入数据的影响,时间复杂度和选择排序一样都是O(n2)。
前端小白,请留言指正!!!