什么是动态规划

 动态规划，说实在的我第一眼看到这个名字，还是上大二的时候。听名字真的很高大上的，甚至有点不知所云的意味在里面。在学校上课的时候一般的课程安排时会把贪心算法和动态规划放作一章的内容进行相应的讲解，因为他们出发的目的相同都是为了寻求最优解。（圈重点来啦!!）动态规划是干嘛的？就是为了能够得到最优解才存在的。
 在动态规划中，我们引入一个叫做OPT的概念（局部最优解），需要得到全局的最优解，我们就需要得到局部的最优解。随后就引入了动态规划的核心思想，通过求得一个个局部最优解得到最终的最优解。

一 斐波那契数列

 上面说了动态规划是用来解决什么问题的以及动态规划的核心思想，可如何去求得一个个局部最优解？通过斐波那契数列我们做一个简单的认识吧。

 其实这道题如果采用暴力法去做很容易，但其实这套题是一道很好的入手动态规划的题目

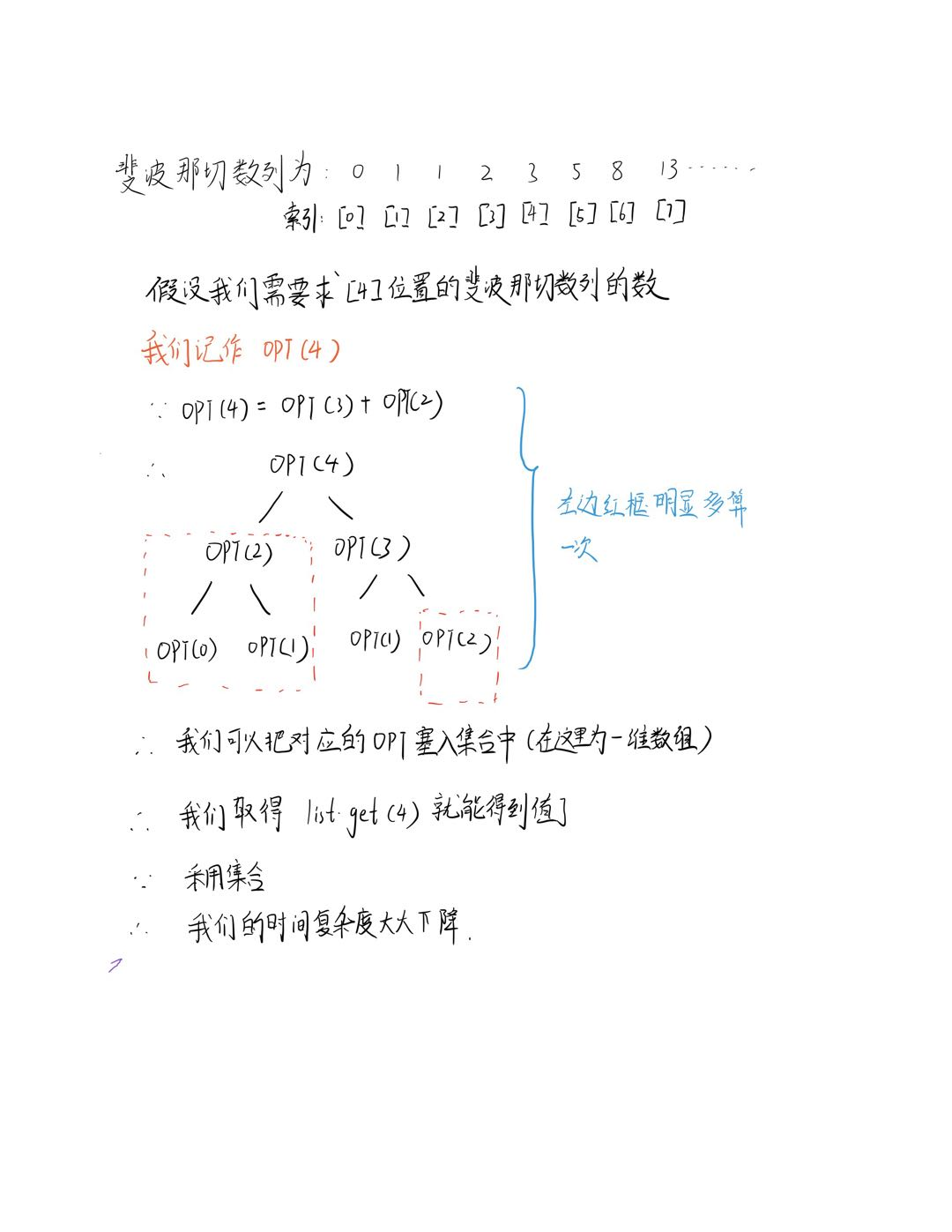
代码

class Solution {
    public int fib(int N) {
        //定义斐波那契数列的记录list
        List fib = new ArrayList();
        //首先把1和2塞进去
        fib.add(0);
        fib.add(1);
        //
        for (int i = 2;i<N+1;i++){
            fib.add((int)fib.get(i-2)+(int)fib.get(i-1));
        }

        return (int)fib.get(N);
    }
}

二 工人做任务问题

循序渐进，我们来看一道选择工作需要考虑:工时以及工人所获得金钱的问题

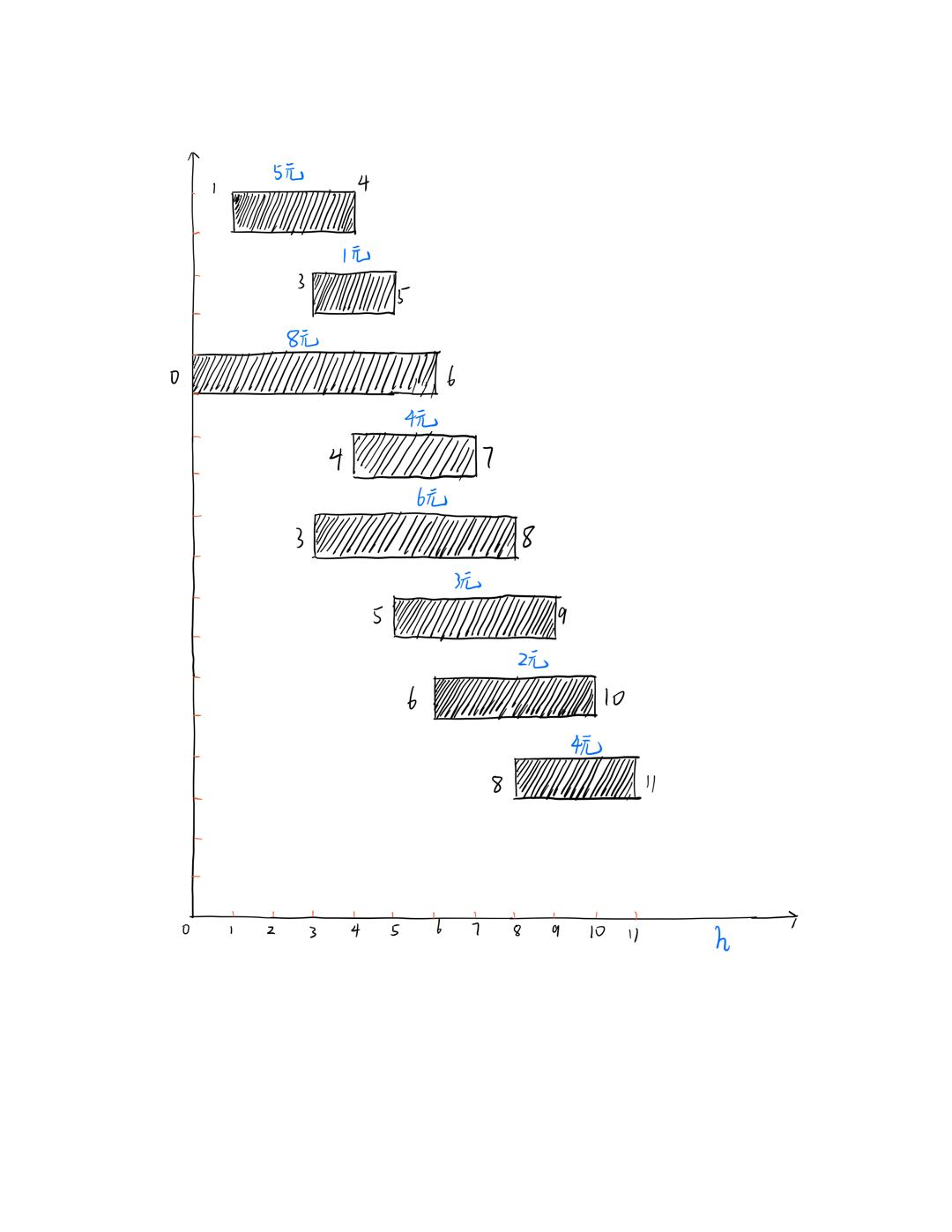
 这道题的大体意思在于，我们如何选择才能保证我们所获得的收益最大。
 思路如下：

三 最大值

 选择一堆不相邻的数字使得和最大
 例子：arr =[1,2,4,1,7,8,3]
    return 15;

思路

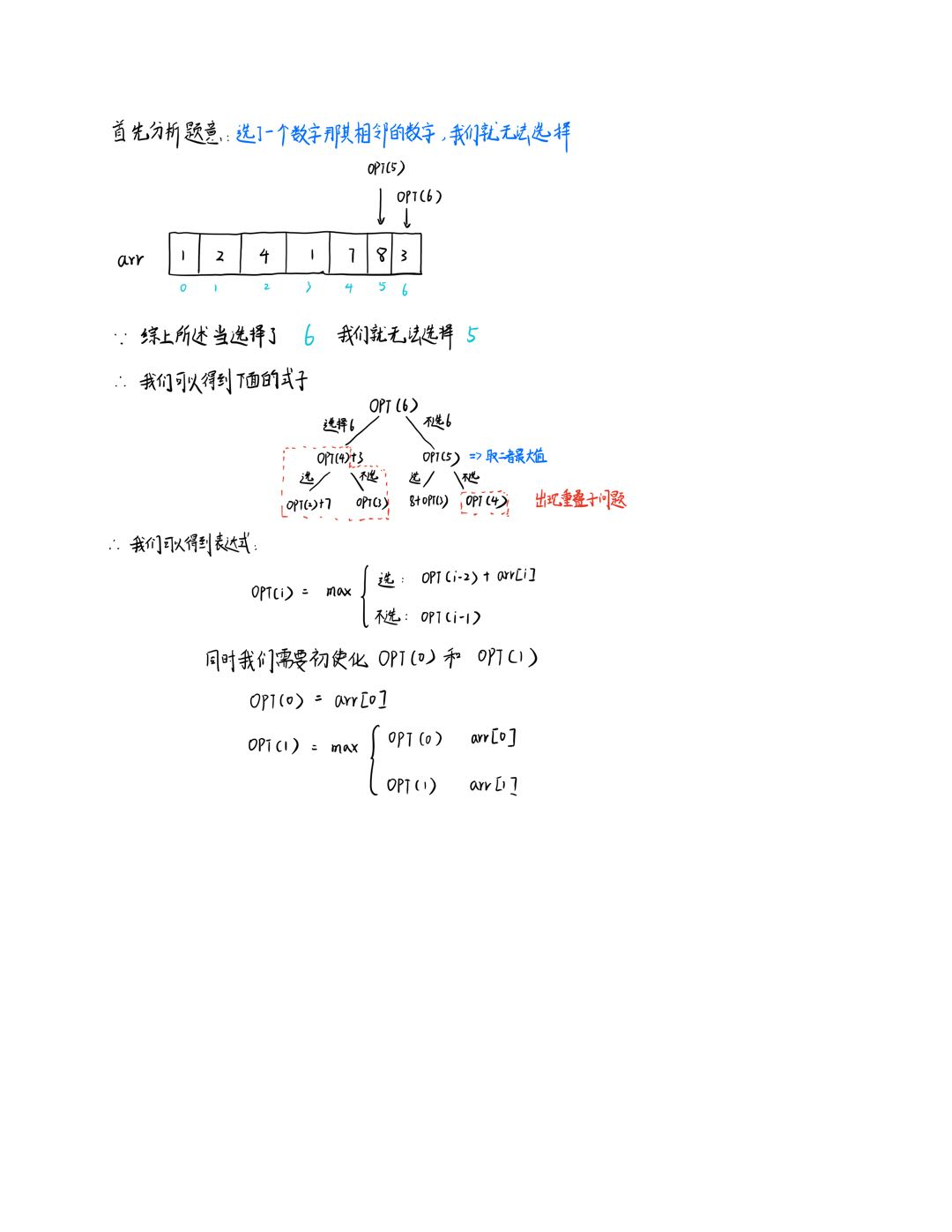
代码

public int findBiggestSum(int[] nums ){
        //新建一个dp数组
        int [] dp = new int[nums.length];

        //初始化dp数组的前两位
        dp[0] = nums[0];
        dp[1] = Math.max(nums[0],nums[1]);

        //将剩下的dp数组填补完整
        for (int i=2 ; i<dp.length ; i++){
            int numberA = dp[i-2]+nums[i];
            int numberB = dp[i-1];
            dp[i]= Math.max(numberA,numberB);
        }

        return dp[nums.length-1];
    }

四  求得是否可构成目标值

  给定一个目标值（targert），同时给定一串数组arr，其中arr与target的数字都为正整数，求得这些数字能否构成target
 例子：arr = [3,34,4,12,5,2]
    target = 9;
    return true;

思路

代码

    public boolean dpSubset(int[] nums , int target){
        //新建一个二维数组
        boolean[][] dp = new boolean[nums.length][target+1];

        //填补第一列
        for (int i =1 ;i<dp.length;i++){
            dp[i][0] = true;
        }

        //填补第一行
        for (int i = 0 ; i<dp[0].length;i++){
            dp[0][i] = false;
        }

        //第一列中 剩余值等于nums[0]的依据判定条件肯定是true
        dp[0][nums[0]] = true;

        //填补二维数组
        for (int i= 1 ; i<dp.length;i++){
            for (int j=1;j<target+1;j++){
                //如果当前大于target 那证明我们就不能选他只能让他等于 i-1
                if (nums[i]>j) dp[i][j] = dp[i-1][j];
                else {
                    //取得subset 看是不是 符合条件 获得那个地方的boolean值
                    boolean numberA = dp[i-1][target-nums[j]];
                    //当我们不选的时候直接取i-1
                    boolean numberB = dp[i-1][j];
                    dp[i][j] = numberA||numberB;
                }
            }
        }
        //返回右下角
        return dp[nums.length-1][target];
    }

总结

以上的几道题 可以循序渐进的初步认识动态归化 总结也希望能帮到别人