序
文章中用到的代码已整理放在
欢迎star一起学习!
数据结构
在开始学习数据结构之前,先说说为什么会有数据结构,以及为什么要使用数据结构,结合所学的关于操作系统的知识,笔者认为是计算机在进行内存管理的时候,会产生内存碎片、因此为了让内存的利用效率更高,所以才有了各种数据结构。下面所说的数据结构其实也分为两种、线性和非线性的结构。
举个例子,前端经常接触的数组就是线性结构,数组是一段连续分配的内存,因此如果计算机内存中全部都是这样的连续内存的话,各个程序所占内存不一样,这样的话就会出现所谓的内存碎片,所以也有像链表这样的结构,不是连续的,而是通过指针将各个内存片段连接起来。
另外需要注意的是,计算机中的数组都是一块固定的内存空间,大小在一开始就是固定的,添加删除元素,以及扩容开销其实是比较大的,这个不像 js 中的数组,js 的数组是对象的一种,因此不存在上述中的问题。
通过数组这个例子,我们可以看到其实每种结构都是有自己的适用场景,没有说哪种数组结构是最好的,最好的一般都是最合适的。
栈
栈结构我们可以理解为堆在桌子上的书,放在最下面的书只能最后拿出来,而放在最上面的书则是可以最先拿出来,这就是栈的LIFO,后进先出。
栈就是在一段数据的一端进行操作,因此栈的操作会非常快,并且也比较容易去实现。在 JS 中的执行栈就是栈结构的,每次执行一条语句或方法,都会将其压入栈中,如果方法中嵌套了方法,就先压入外层方法,再压入内层方法,因此出栈的时候会是内层方法先执行先出栈,然后才到外部方法执行出栈。
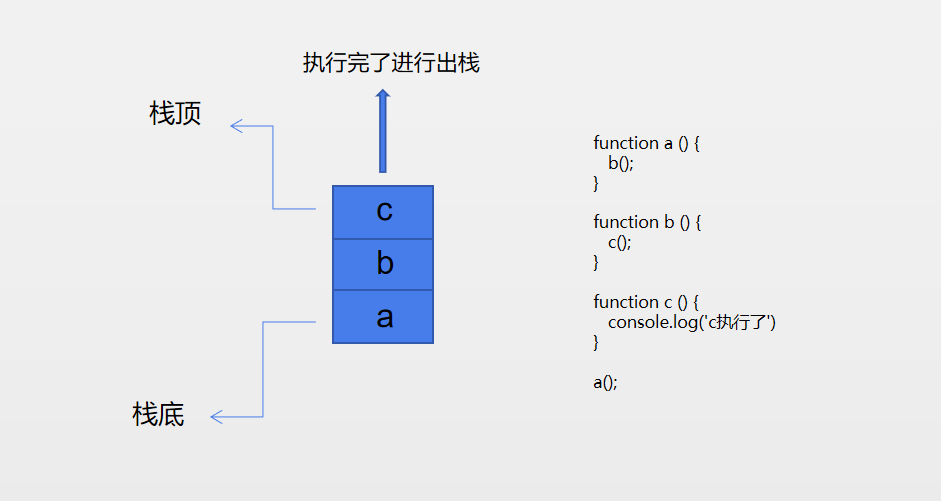
接下来就用 JS 来实现栈的数据结构,主要有这么几个重要的方法:入栈、出栈和查看栈顶的元素。
function Stack() {
this.dataSource = []
this.push = push
this.pop = pop
this.peek = peek
}
// 入栈
function push(elem) {
this.dataSource.push(elem)
}
// 出栈
function pop() {
this.dataSource.pop()
}
// 查看栈顶元素
function peek() {
// 注意这里查看栈顶元素不是删除栈顶元素,因此我们选择数组中最后一个元素返回即可
// 如果栈中没有数据的话,则返回null
return this.dataSource[this.dataSource.length - 1] || null
}
来看一个栈结构的应用,利用栈结构来将十进制转成二进制
/**
* 十进制转二进制的利用栈的数据结构
* @param {number} decNumer 需要进行转换的数字
*/
function dec2bin(decNumer) {
const stack = new Stack()
while (decNumer > 0) {
stack.push(decNumer % 2)
decNumer = Math.floor(decNumer / 2)
}
let binStr = ''
while (!stack.isEmpty()) {
binStr += stack.pop()
}
return binStr
}
同样通过这个案例,我们也可以实现任意进制的转换,代码这里就不给出了,有兴趣可以自己来实现一下。
队列
队列结构和栈结构是比较相似的,队列的特点是FIFO,先进先出,可以理解为排队买奶茶,队首的人先付账买奶茶,如果还有人想要买,那么只能从队尾开始排队,队首的人买完奶茶,则从这个队列退出。
在 js 中的队列,事件循环就是其中之一。js 是单线程,遇到异步任务的时候,会将任务加入一个队列中,档主线程空闲的时候,按照加入队列的顺序,一个一个的执行队列中的任务。
因此我们也可以发现队列有两个重要的操作,出队和入队,结合栈的操作,来看看实现的代码:
function Queue () {
this.data = []
}
// 入队
Queue.prototype.enqueue = function (ele) {
this.data.push(ele)
}
// 出队
Queue.prototype.dequeue = function () {
return this.data.shift()
}
// 查看队首元素
Queue.prototype.front = function () {
return this.data[0]
}
// 查看队列是否为空
Queue.prototype.isEmpty = function () {
return this.data.length === 0
}
// 查看队列长度
Queue.prototype.size = function () {
return this.data.length
}
// 查看队列成员
Queue.prototype.toString = function () {
let ret = ''
for (let i = 0; i < this.data.length; i++) {
ret += this.data[i] + ''
}
return ret
}
接下来再说一种特殊的队列,叫做优先级队列,所谓优先级,就是队列中的每个成员都有一个优先级,优先级高的成员可以插入优先级低的成员的前面。
举个例子,在医院排队就诊的病人,医院会根据病人的患病紧急程度安排就诊顺序,这个就是优先级队列的一种实现。
根据以上的理解,优先级队列的代码实现方式也有两种,一种就是每个插入的成员按照优先级高低来进行排序,出队的时候则按照正常的删除队首元素即可;另外一种则是插入的时候正常排在队尾,但是出队的时候,会删除优先级最高的成员,按照医院排队的例子,就是每个人按顺序挂号,但是如果有病种的患者,则可以优先就诊。
来看看优先级队列的实现代码
// 队列成员
function QueueElem (elem, priority) {
this.elem = elem
this.priority = priority
}
// 优先级队列
function PriorityQueue () {
this.data = []
}
// 入队
PriorityQueue.prototype.enqueue = function (elem, priority) {
const priorityElem = new QueueElem(elem, priority)
// 优先级队列长度为0时,直接将元素添加进去
if (this.data.length === 0) {
this.data.push(priorityElem)
} else {
let isAdd = false
for (let i = 0; i < this.data.length;i++) {
// 如果插入的元素的优先级比当前的元素高,那么就插入当前元素的前面的位置
if (priority < this.data[i].priority) {
this.data.splice(i, 0, priorityElem)
isAdd = true
break
}
}
// 如果插入的元素比当前队列中的所有的元素优先级都要低,那么就插入队尾
if (!isAdd) {
this.data.push(priorityElem)
}
}
}
// 出队
PriorityQueue.prototype.dequeue = function () {
return this.data.shift()
}
// 查看队首元素
PriorityQueue.prototype.front = function () {
return this.data[0]
}
// 队列是否为空
PriorityQueue.prototype.isEmpty = function () {
return this.data.length === 0
}
// 队列长度
PriorityQueue.prototype.size = function () {
return this.data.length
}
// 查看队列成员
PriorityQueue.prototype.toString = function () {
let ret = ''
for (let i = 0; i < this.data.length; i++) {
ret += this.data[i].elem + this.data[i].priority + '\n'
}
return ret
}
另外一种出队删除优先级最高的成员留给大家思考。
链表
js 中的数组其实是由对像来实现的,他并不像其他语言中的数组那样,操作效率会比较低,这个时候可以考虑用链表来进行操作。链表的插入删除操作的效率要比数组高很多,只需要改变节点的指向即可插入或删除节点,但是如果要进行查找元素的操作的话,链表无法从中间开始查找,必须从头一个个遍历节点。所以如果是插入和删除的操作的话,则可以考虑使用链表操作。
链表就是各个节点通过指针连接在一起组成的结构,链表分为单向链表、双向链表、循环链表等,这里只会和大家说说前两者的实现。
下面结合代码和示意图来说明链表结构,先来说说单向链表。单向链表就是每个节点有一个指针指向下一个节点,并且有一个head指针,指向链表的第一个元素,有一个tail指针指向链表的尾部,那么就是下面这样一个结构:
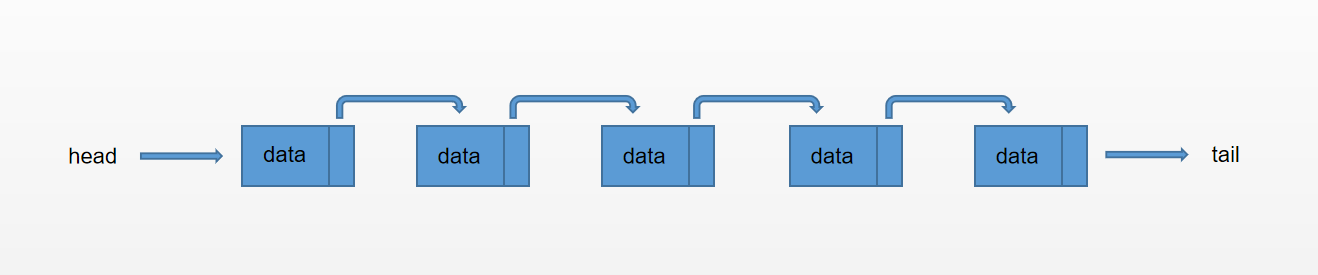
链表的每一个节点和单向链表看起来是这样的:
/**
* 链表节点
* @param {any} element 链表节点保存数据
*/
function Node(element) {
this.element = element
this.next = null
}
// 单向链表
function LinkedList() {
this.head = null
this.length = 0
}
接下来则是重点的插入和删除节点操作:
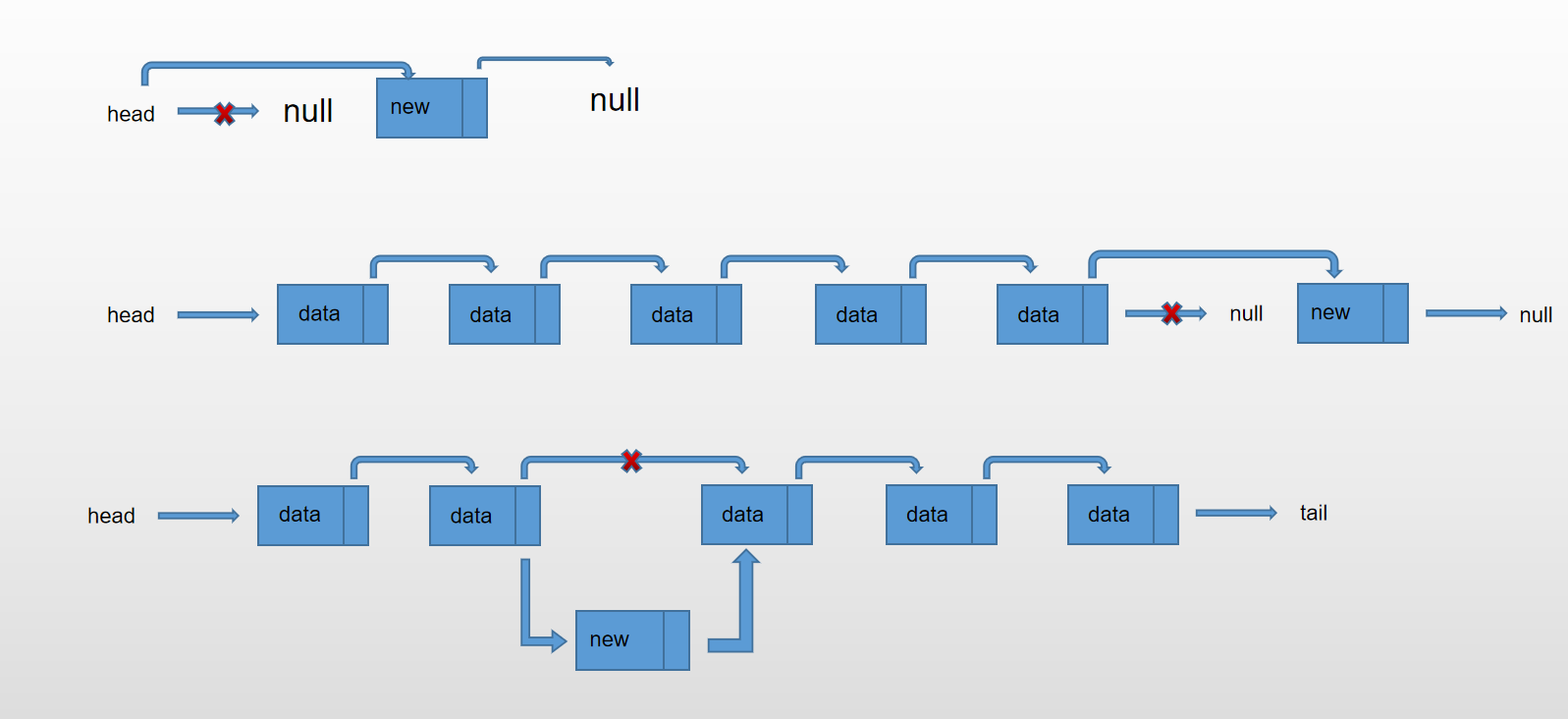
可以看到插入节点分为三种情况,一种是空链表插入节点,直接将head指针指向要插入的节点即可,另外则是往链表尾部插入节点,分为以下几个步骤
- 找到链表尾部节点
- 将尾部节点的下一个节点指向新节点
下面的代码展示了如何在这两种情况下插入节点
LinkedList.prototype.append = function (element) {
const newNode = new Node(element)
// 如果链表为空,则直接将head节点指向新节点
if (this.length === 0) {
this.head = newNode
} else {
// 从头部开始,判断下一个节点是否为空,如果为空,则代表当前节点为链表的最后一个节点
// 则把当前节点的next引用赋给新节点
let currentNode = this.head
while (currentNode.next) {
currentNode = currentNode.next
}
currentNode.next = newNode
}
// 链表长度记得+1
this.length++
}
最后来看看如何往指定位置插入新节点,根据上图,我们也有以下几步:
- 设置currentNode节点,表示当前遍历到的节点,从head节点开始。
- 如果currentNode节点的索引等于要找的位置,那当前的currentNode就是要插入新节点的位置。
- 将新节点的下一个节点指向原来currentNode的下一个节点。
- 将currentNode的下一个节点指向新节点。
注意:3、4步的顺序不能替换、原因就是当前节点的下一个节点会赋值给下一个节点,这样当前节点的下一个节点的引用被改变了,新节点就无法指向这个节点了。
/**
* @param {number} position 要插入的元素位置
* @param {element} element 要插入链表的元素
*/
LinkedList.prototype.insert = function (position, element) {
// 边界处理
if (position < 0 || position > this.length) return false
const newNode = new Node(element)
if (position === 0) {
newNode.next = this.head
this.head = newNode
} else {
// 从1开始计数,因为position为0时的情况上面已经处理过了
let count = 1
let currentNode = this.head
while (count++ < position) {
currentNode = currentNode.next
}
// 顺序不能变
newNode.next = currentNode.next
currentNode.next = newNode
}
this.length++
return true
}
好了,有了插入节点的实例,那么接下来的删除节点也就很简单了。
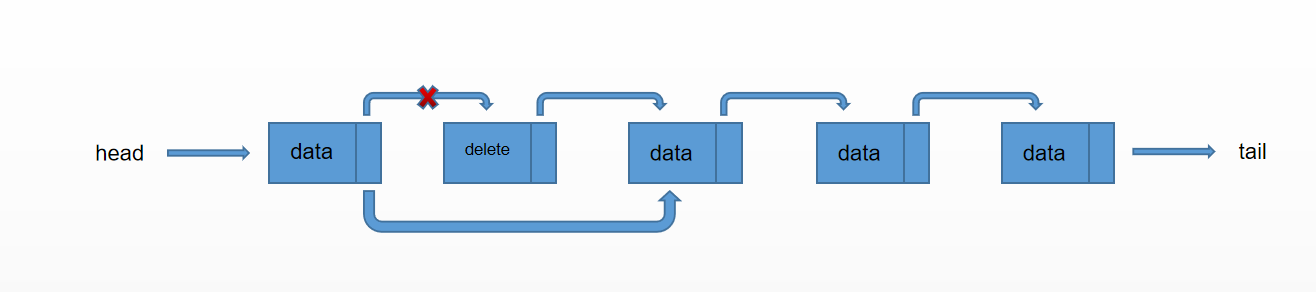
如图我们有以下几步,来删除一个指定位置的节点:
- 找到要删除的节点。
- 找到要删除的节点的上一个节点。
- 将要删除的节点的上一个节点的下一个节点指向要删除的节点的下一个节点。
这个文字描述起来比较难理解,所以对着这个图慢慢理解一下,这里有一个问题,就是我们没有将要删除的节点的下一个节点指向null,原因就是删除节点现在已经没有节点指向他了,即使他有指向别的节点,垃圾回收也会将删除节点的引用一并清除的。
现在我们是删除指定位置的节点,那如果是删除指定的节点呢?其实也很简单,只要先找出指定节点的位置,那就变成了上面的根据指定位置来删除节点了。
看看删除指定节点的代码实现:
// 找到指定节点的位置
LinkedList.prototype.indexOf = function (element) {
let currentNode = this.head
let index = 0
while (currentNode) {
if (currentNode.element === element) {
return index
}
currentNode = currentNode.next
index++
}
return -1
}
// 删除指定位置的节点
LinkedList.prototype.removeAt = function (position) {
// 处理边界
if (position < 0 || position > this.length - 1) return false
let currentNode = this.head
if (position === 0) {
this.head = this.head.next
} else {
let count = 0
let previous = null
while (count++ < position) {
previous = currentNode
currentNode = currentNode.next
}
previous.next = currentNode.next
}
// 记得删除完以后,长度-1
this.length--
return true
}
// 删除指定节点
LinkedList.prototype.remove = function (element) {
const index = this.indexOf(element)
return this.removeAt(index)
}
有了上面单向链表的基础知识,我们就能构造出双向链表,所谓双向链表,其实就是比单向链表多了一个指针,用来指向节点的上一个节点。
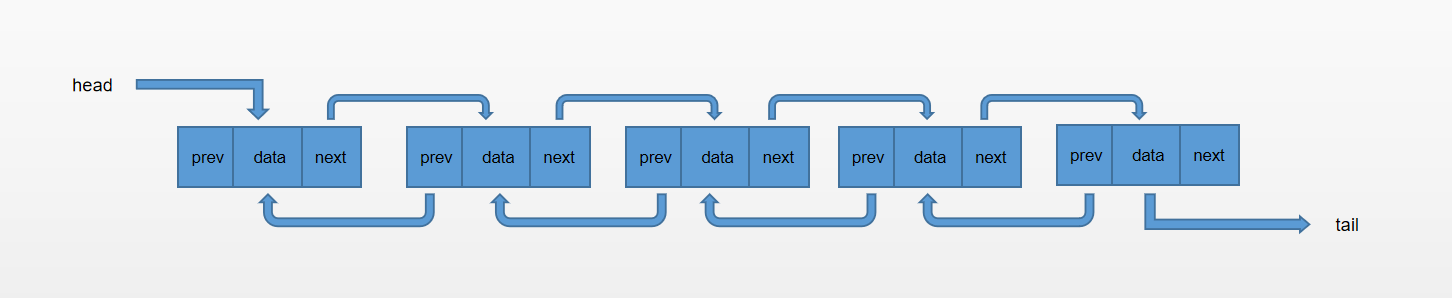
这里就不详细分析双向链表的具体操作,直接展示完整代码:
// 双向链表
function DNode (element) {
this.element = element
this.next = null
this.prev = null
}
function DoublyLinkedList () {
this.head = null
this.tail = null
this.length = 0
}
DoublyLinkedList.prototype.append = function (element) {
const newNode = new DNode(element)
if (this.length === 0) {
this.head = newNode
this.tail = newNode
} else {
let currentNode = this.head
while (currentNode.next) {
currentNode = currentNode.next
}
currentNode.next = newNode
newNode.prev = currentNode
this.tail = newNode
}
this.length++
}
DoublyLinkedList.prototype.insert = function (position, element) {
const newNode = new DNode(element)
if (position < 0 || position > this.length) return false
if (this.length === 0) {
this.head = newNode
this.tail = newNode
} else {
if (position === 0) {
newNode.next = this.head
this.head.prev = newNode
this.head = newNode
} else if (position === this.length) {
this.tail.next = newNode
newNode.prev = this.tail
this.tail = newNode
} else {
let currentNode = this.head
let count = 0
while (count++ < position) {
currentNode = currentNode.next
}
newNode.next = currentNode
newNode.prev = currentNode.prev
currentNode.prev.next = newNode
currentNode.prev = newNode
}
}
this.length++
return true
}
DoublyLinkedList.prototype.indexOf = function (element) {
let currentNode = this.head
let index = 0
while (currentNode) {
if (currentNode.element === element) {
return index
}
currentNode = currentNode.next
index++
}
return -1
}
DoublyLinkedList.prototype.removeAt = function (position) {
if (position < 0 || position > this.length - 1) return null
let currentNode = this.head
// 删除元素的时候,当链表长度为0时返回null
if (this.length === 1) {
this.head = null
this.tail = null
} else {
if (position === 0) {
this.head.next.prev = null
this.head = this.head.next
} else if (position === this.length - 1) {
this.tail.prev.next = null
this.tail = this.tail.prev
} else {
let index = 0
while (index++ < position) {
currentNode = currentNode.next
}
currentNode.prev.next = currentNode.next
currentNode.next.prev = currentNode.prev
}
}
this.length--
return currentNode.element
}
DoublyLinkedList.prototype.remove = function (element) {
const index = this.indexOf(element)
return this.removeAt(index)
}
最后就是循环链表,顾名思义,就是首尾相连的链表

可以看到链表的结尾再次指向了head,其他其实和单向链表是一样的,那么如何让链表首尾相连呢。可以通过加入下面的代码来实现:
// 省略重复代码
this.head.next = this.head
就这么简单的一句代码可以让首尾相连,大家可以细品这句做了什么工作,具体代码就不实现了,一般如果需要从后向前遍历节点的时候,又不想创建双向链表的话,则可以使用循环链表代替,从链表尾部节点向后移动就等于从后往前遍历。
字典
字典在 js 中对象就是通过这种形式来实现的,简单来说就是 key-value 结构,和我们理解 js 中的对象是一样的。
字典结构有以下的特点:
- 字典的主要特点是一一对应的关系
- 字典中的key不可以重复,但是value是可以重复的,并且key是无序的
- 这种映射关系在某些编程语言中也可以称之为Map
在 js 中我们使用对象来实现字典结构,主要在于添加元素时需要判断字典中是否已经包含该键,因为字典中的键都是唯一的,其他就是简单的取对象属性的操作了。
function Dictionary() {
this.data = {}
}
Dictionary.prototype.has = function (element) {
return this.data.hasOwnProperty(element)
}
Dictionary.prototype.add = function (element) {
if (this.has(element)) return false
this.data[element] = element
return true
}
Dictionary.prototype.delete = function (element) {
if (!this.has(element)) return false
delete this.data[element]
return true
}
Dictionary.prototype.clear = function () {
this.data = {}
}
Dictionary.prototype.size = function () {
return Object.keys(this.data).length
}
Dictionary.prototype.values = function () {
return Object.keys(this.data)
}
Hash(散列)
hash 其实是一种存储数据的方法,也可以称为算法,并不是数据结构,hash表(散列表)才是数据结构。hash表具有添加、删除及取用数据非常快的优点,同时他也有不足的地方:
- 空间利用率不高
- 哈希表中的元素是无序的
- 不能快速找出哈希表的如最大值和最小值等特殊值
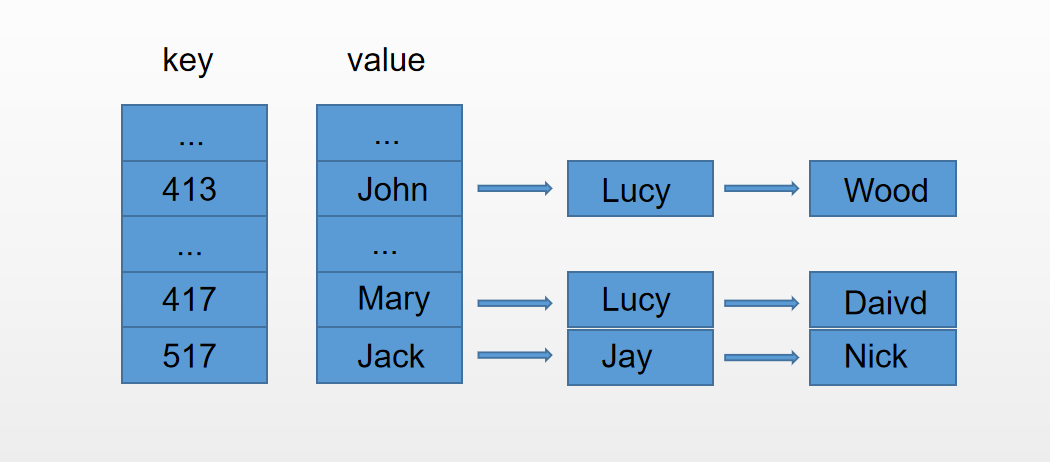
例如通过某种方法将一组号码簿存储到hash表中,如下图所示

这个某种方法就是将原来的号码经过一些计算,映射成hash表中唯一的键,这个方法就叫做哈希函数,而这个将号码映射为唯一索引的过程就叫做哈希化。当存储的数据越来越多的时候,就可能会存在多个输入的key会映射到同一个索引,这个就叫做碰撞。
先来设计一个简单的哈希函数,利用字符的ASCII值当做key
function simpleHash(data) {
let total = 0
for (let i = 0; i < data.length; i++) {
total += data.charCodeAt(i)
}
return total / this.table.length
}
通过这种哈希函数的话,得到相同key的可能性还是比较大的,先来说说碰撞的解决方法,然后再去设计一个更好的哈希函数:
- 链地址法(拉链法)
- 开放地址法(寻址法)寻找空白的单元格添加重复的数据
-
线性探测 聚集问题 一连串填充单元
-
二次探测 对探测步长优化
-
再哈希法
-
链地址法,就是发生碰撞的时候,将value变成数组或者链表结构,而不再是原来只能存储一个数据的情况,这样的话,当获取某个key对应的value时,得到的则是一个数组或者是链表。
线性探测法,则是发生碰撞的时候,去寻找下一个空白的位置,根据哈希表的一个结构,可以知道表中会有一些空间是闲置的,因此线性探测就是在碰撞的时候找到这些闲置的空间,并将发生碰撞的值存储在这些空间当中。需要注意的时,如果需要删除某一个key时,不能直接将key对应的value设置为 null,原因是删除操作的话会影响到下次的查询操作,所以最好删除元素的时候,将删除的元素标记为-1。
线性探测每次的步长为1,这样一个接一个的寻找闲置的单元,这样也会导致一连串的连续的单元聚集在一起,产生聚集问题。带来的后果就是设置或获取某个key时,花费的时间更多,所以接下有了这个二次探测法,则是对步长进行了一定的优化,假设当前查找的元素的位置是x,那么下次查找的位置可以是x + 1^2,以此类推,之后则是x + 2^2, x + 3^2等等。
虽然这样查找可以跳过一些聚集,但是当存储的值变多的时候,依然会产生上面的连续步长的聚集问题,当然这种情况会比线性探测的几率小很多。接下来就是再哈希法,再去设计一个哈希函数,依赖某个设定的关键字,将关键字进行哈希化以后得到的值来作为探测的步长。这个哈希函数,其实已经有一个默认的方法了:
// constant为关键字,最好为质数,且小于数组容量
let stepSize = constant - (key % constant)
现在来设计一个哈希函数就显得非常重要,一个好的哈希函数需要满足下面两个条件:
- 快速计算 (霍纳法则)
- 均匀分布
其中快速计算是指哈希函数的运算时间复杂度要比较低,这里提到了一个概念:霍纳法则,其实就是对于多项式的一种优化算法,降低了多项式运算的时间复杂度。另外均匀分布则是说,我们希望哈希表的空间能够得到充分利用,因此对于每个存储的数据一定要均匀分布,而不是聚集在了某一处地方。
根据这两个条件,来看看下面的更好的一个哈希函数
/**
* @param str 需要进行哈希化的字符串
* @param size 哈希表的长度
* @returns 字符串映射的索引
*/
function hashFn (str, size) {
// 使用霍纳法则进行多项式优化
// 这里采用了37来扩大hashCode
let hashCode = 0
for (let i = 0; i < str.length; i++) {
hashCode = 37 * hashCode + str.charCodeAt(i)
}
return hashCode % size
}
这个哈希函数其实对比上面的简单的哈希函数,其实就是多了一个hashcode。至于为什么hashcode是37,这个大体因为37是一个质数,因为质数的一些数学特质、能够使得得到的索引能够均匀分布在哈希表中,37就是一个哈希表中常用的一个质数。有兴趣可以去了解一下质数的一些特性,这里不详细展开了。
来看看如何利用这个哈希函数去设计一个哈希表:
function HashTable () {
// 存储数据的数组
this.storage = []
// 哈希表中已经存在的元素个数
this.count = 0
// 哈希表的初始容量
this.capacity = 7
}
// 插入数据
HashTable.prototype.put = function (key, val) {
const index = this.hashFn(key, this.capacity)
let bucket = this.storage[index]
if (!bucket) {
bucket = []
this.storage[index] = bucket
}
for (let i = 0; i < bucket.length; i++) {
const tuple = bucket[i]
if (tuple[0] === key) {
tuple[1] = val
return
}
}
bucket.push([key, val])
this.count++
// 如果存储数据的数量大于哈希表容量的0.75,则容量进行扩容,扩容后的容量为质数
if (this.count > this.capacity * 0.75) {
const prime = this.getPrime(this.capacity * 2)
this.resize(prime)
}
}
// 删除数据
HashTable.prototype.remove = function (key) {
const index = this.hashFn(key, this.capacity)
const bucket = this.storage[index]
if (!bucket) return null
for (let i = 0; i < bucket.length; i++) {
const tuple = bucket[i]
if (tuple[0] === key) {
bucket.splice(i, 1)
this.count--
// 如果存储数据的数量小于哈希表容量的0.25,则减少容量,减少后的容量为一个质数
if (this.capacity > 7 && this.count < this.capacity * 0.25) {
const prime = this.getPrime(Math.floor(this.capacity / 2))
this.resize(prime)
}
return tuple[1]
}
}
return null
}
// 扩容或减容
HashTable.prototype.resize = function (capacity) {
const oldStorage = this.storage
this.storage = []
this.count = 0
this.capacity = capacity
for (let i = 0; i < oldStorage.length; i++) {
const bucket = oldStorage[i]
if (!bucket) continue
for (let j = 0; j < bucket.length;j++) {
const tuple = bucket[j]
this.put(tuple[0], tuple[1])
}
}
}
// 判断一个数是否是质数
HashTable.prototype.isPrime = function (num) {
// 如果一个数可以被因式分解的话,则这两个相乘的数字,
// 其中一个一定小于等于这个数,另外一个一定大于等于这个数
// 所以我们只要取这个数的平方根,计算2到平方根之间是否可以被整除
const temp = parseInt(Math.sqrt(num))
for (let i = 2; i < temp; i++) {
if (num % i === 0) {
return false
}
}
return true
}
// 获取一个质数
HashTable.prototype.getPrime = function (num) {
while (!this.isPrime(num)) {
num++
}
return num
}
这里的 hashTable 的实现主要在于动态扩容和减容,计算哈希表中存储数据的数量,如果存储数据的数量大于哈希表容量的0.75,则进行扩容,扩容就是将容量缩小一半,然后传入判断质数的方法,得到一个质数来作为扩容后的容量,同样缩容也是如此。
树
树在 js 中遇到的可能不多,不过像一些虚拟dom中能够经常看到他的身影。树结构的种类也非常多,一般用的比较多的也就是二叉树了。
树结构是非线性的,可以表示一对多的关系,综合了其他数据结构的一些优点,并且也弥补了其他数据结构的缺点,例如,树结构是有序的,并且可以很快查找出最大值、最小值这样的特殊值。
先来看关于树的一些概念:
- 树:n(n >= 0)个节点构成的有限集合,n = 0时成为空树
- 根(Root):在第一层的节点
- 子树(SubTree):父节点左右节点构成的完整树
- 父节点
- 子节点
- 兄弟节点
- 节点的度(Degree):节点的子树个数
- 树的度:树的节点中最大的度
- 叶节点(Leaf):度为0的节点
- 节点的层次:根节点在1层,其他各层在父节点的层次+1
- 树的深度:树中节点的最大层次
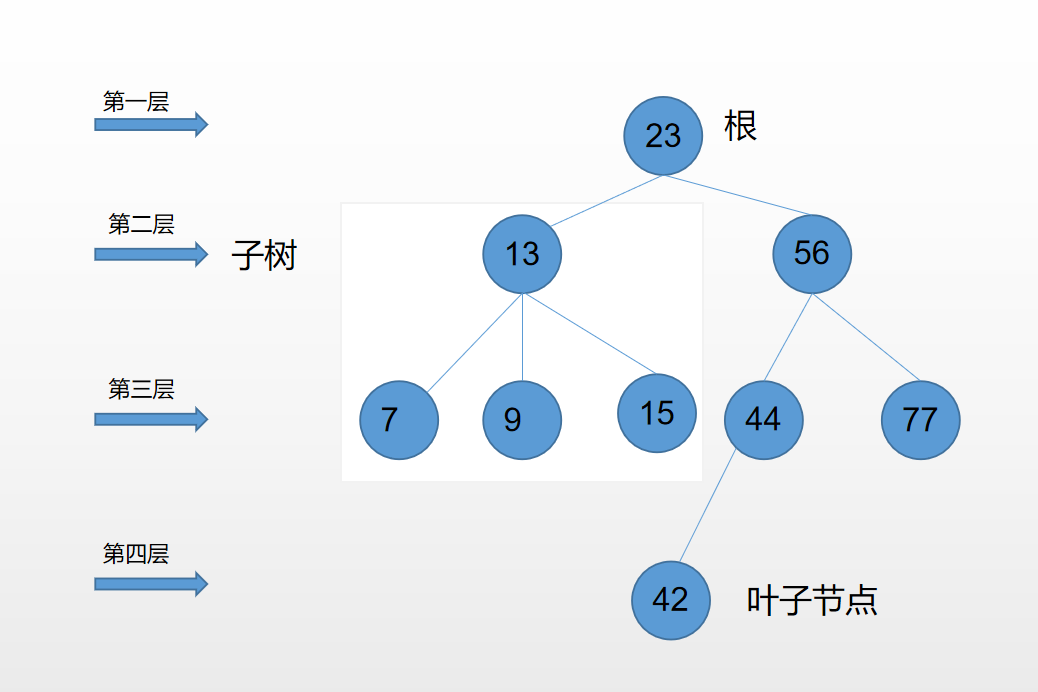
常见的树的一些种类:
- 二叉树
- 完美二叉树(满二叉树)
- 完全二叉树
- 二叉搜索树(BST)
- 平衡树
- AVL树
- 红黑树
大体知道树的一些种类后,主要是展示一下前端比较常用的二叉搜索树的实现。先来看看二叉搜索树的一些特性:
- 二叉搜索树是二叉树,可以为空
- 非空左子树的所有值小于其根节点的值
- 非空右子树的所有值大于其根节点的值
- 左右子树本身也是一颗二叉搜索树
有了这些特性之后,先从简单的说起,来看看如何去遍历一颗二叉树,主要三种遍历方法:
- 先序遍历,从根节点开始,然后到左子树,最后到右子树。
- 中序遍历,先访问左子树,然后到根节点,最后访问右子树。中序遍历实际就是以升序来访问树上的所有节点。
- 后续遍历,先访问叶子节点,再访问左右子树。
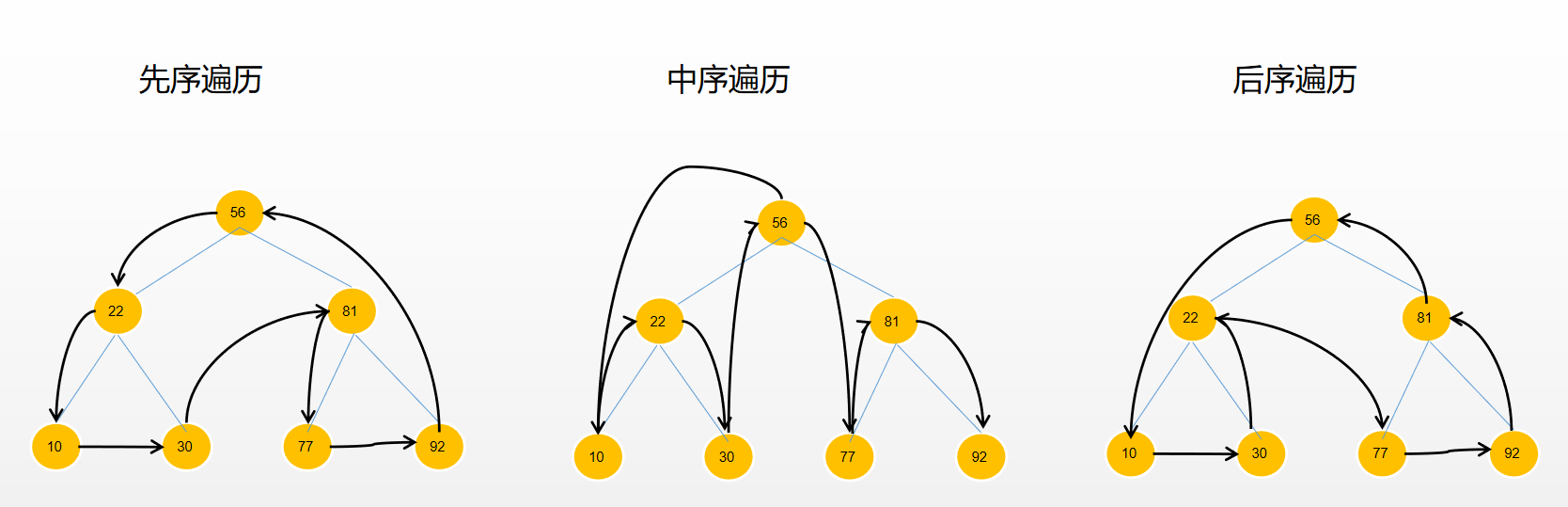
按照这个思路,下面直接上代码:
function Node(data) {
this.data = data
this.left = null
this.right = null
}
function BST() {
this.root = null
}
// 先序遍历
BST.prototype.preOrder = function() {
preOrderTraverse(this.root)
}
// 中序遍历
BST.prototype.inOrder = function() {
inOrderTraverse(this.root)
}
// 后序遍历
BST.prototype.postOrder = function() {
postOrderTraverse(this.root)
}
function preOrderTraverse(node) {
if (node !== null) {
console.log('preOrder:' + node.data)
preOrderTraverse(node.left)
preOrderTraverse(node.right)
}
}
function inOrderTraverse(node) {
if (node !== null) {
inOrderTraverse(node.left)
console.log('inOrder:' + node.data)
inOrderTraverse(node.right)
}
}
function postOrderTraverse(node) {
if (node !== null) {
postOrderTraverse(node.left)
postOrderTraverse(node.right)
console.log('postOrder:' + node.data)
}
}
说完二叉搜索树的遍历,接着就来说说比较复杂的部分,二叉搜索树的添加和删除节点。
添加节点相对而言简单一点,主要分为两种情况:一种就是往空树中插入节点,那么直接将根节点指向要插入的节点即可。另外一种则是根节点存在的情况下。这时可以用递归,也可以用迭代的方法来解决。我们主要来说说递归的思路。要插入一个新节点,肯定需要判断新节点的值应该被放在哪个位置,于是从根节点开始,先判断根节点的值和要插入节点值的大小比较,如果比根节点大,那就去根节点的右子树去继续遍历,如果比根节点小,那则去根节点的左子树去找。
根据这个思路代码实现就很明了了:
BST.prototype.insert = function(data) {
const newNode = new Node(data)
// 如果根节点不存在
if (!this.root) {
this.root = newNode
} else {
// 使用递归方法遍历二叉树,插入合适的位置
insertNode(this.root, newNode)
// 使用循环的方法
// 定义指向当前遍历到的节点的引用
// let current = this.root
// 保存遍历节点的父节点的引用
// 后续需要把新节点挂载到这个引用上
// let parent
// 遍历整棵树
// while(true) {
// parent = current
// 如果要插入的节点的值小于遍历节点的值
// 继续往当前节点左边节点遍历
// if (data < current.data) {
// current = current.left
// if (current === null) {
// parent.left = newNode
// break
// }
// } else {
// current = current.right
// if (current === null) {
// parent.right = newNode
// break
// }
// }
// }
}
}
function insertNode(current, newNode) {
if (newNode.data < current.data) {
if (current.left === null) {
current.left = newNode
} else {
insertNode(current.left, newNode)
}
} else {
if (current.right === null) {
current.right = newNode
} else {
insertNode(current.right, newNode)
}
}
}
如果是迭代的方法的话,那就是一层层的循环遍历去找到适当的插入位置。
说完插入节点,删除节点的情况相对就更复杂一些了。
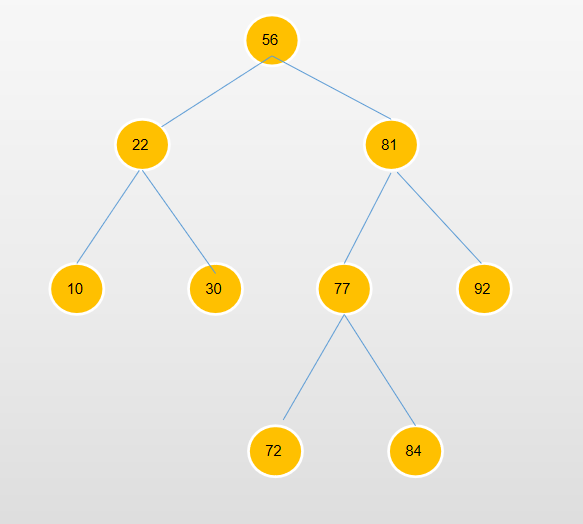
首先我们需要一个值来保存删除节点的父节点,因为到时候肯定需要这个父节点来改变左右子节点的指向,另外就是还需要一个值来判断这个被删除节点是父节点的左子节点还是右子节点,这个则是需要后续在父节点上来指定改变的是左子节点的引用,还是父子节点的引用。
我们来根据上图展示删除节点的几种情况:
- 删除的节点是叶子节点,并且删除节点的父节点为根节点,那么直接将根节点指为null。
- 删除的节点是叶子节点,并且删除节点的父节点不是根节点,如果删除节点是父节点的左子节点,那么父节点的left节点指向null,否则 right节点指向null。
- 删除的节点只有一个左子节点,删除节点是父节点的左子节点,那么就将父节点的左子节点指向删除节点的左子节点即可,如果删除节点是父组件的右子节点,就将父节点的右子节点指向删除节点的左子节点。
- 如果删除的节点有两个子节点,那么又会有以下图中显示的这些情况。
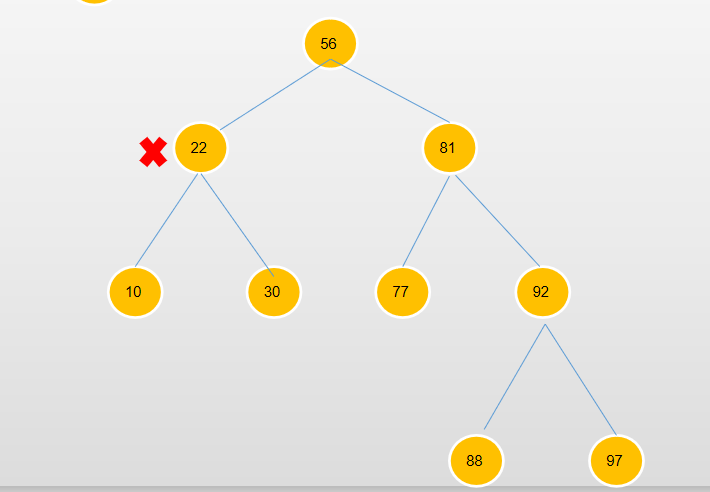
如果删除节点22的话,可以直接将节点10或者是节点30提到节点22的位置都能保证二叉搜索树的特性。如果删除的节点是81呢,又该如何做呢?
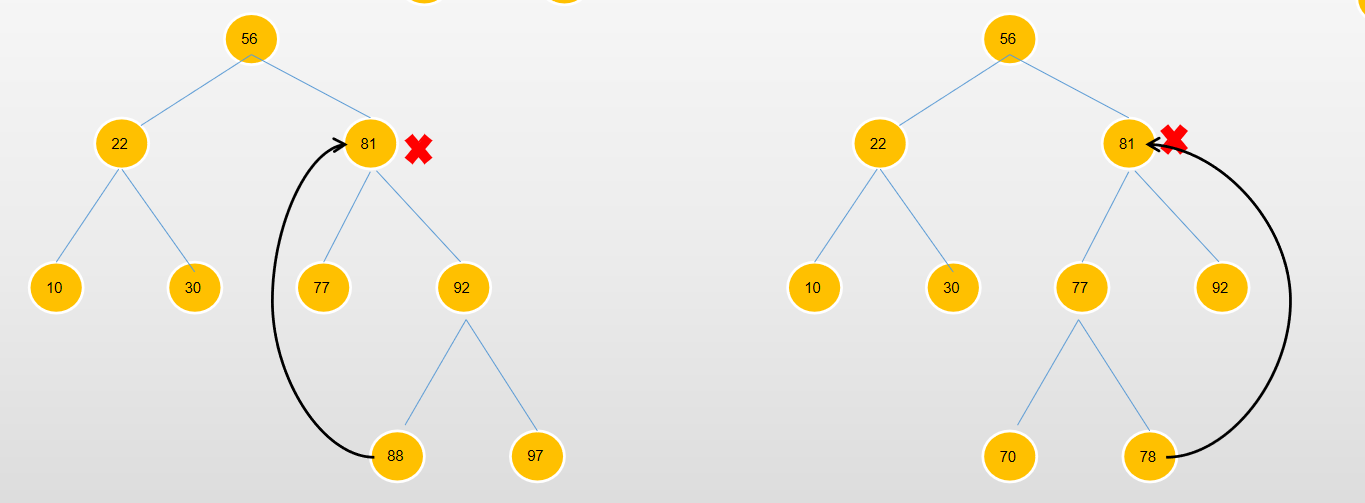
看上左图,可以选择将节点77提到删除节点的位置,那如果是将节点92提上去,我们就将节点92的子树提上去,再去改变节点77,将节点88的左子节点指向节点77,也能满足条件。那如果是将88提上去是否可以呢,又或者是97提上去呢。所以对于删除节点来说,重要的地方就在于找到删除节点的后继节点,使得依然满足二叉搜索树的条件。
通过不断的往88节点上面加子节点,也能推断出这样一个结论,如果我们要找被删除节点的左子树上的节点来替代被删除节点的话,那其实就是找被删除节点左子树的最大值的叶子节点,如上右图,如果节点78还有一个右子节点的话,那么选择替换的节点就是这个右子节点,也就是整个左子树的最大值节点,反之,如果选择的是右子树的节点替换删除节点的话,则挑选右子树上最小的节点。
好了,有了这些分析,就来完成一下二叉搜索树的删除节点逻辑,这里我们以寻找右子树的节点替换删除节点:
BST.prototype.remove = function(data) {
let current = this.root
// 保存删除节点的父节点以及删除节点位于父节点的左边还是右边
let parent, isLeft
// 查找要删除的值
while (current.data !== data) {
parent = current
if (data < current.data) {
current = current.left
isLeft = true
} else {
current = current.right
isLeft = false
}
}
// 如果删除的值不存在
if (current === null) return false
// 如果删除的是叶子节点
if (current.left == null && current.right == null) {
// 如果删除的节点是根节点
// 如果删除的节点是父节点的左子节点
// 如果删除的节点是父节点的右子节点
if (current == this.root) {
this.root = null
} else if (isLeft) {
parent.left = null
} else {
parent.right = null
}
}
// 如果删除的节点只有一个子节点
else if (current.left === null) {
if (current === this.root) {
this.root = current.right
} else if (isLeft) {
parent.left = current.right
} else {
parent.right = current.right
}
}
else if (current.right === null) {
if (current === this.root) {
this.root = current.left
} else if (isLeft) {
parent.left = current.left
} else {
parent.right = current.left
}
}
// 删除的节点有两个子节点(查找后继节点为例)
// 需要改变父节点的指向,指向后继节点
// 需要将后继节点的左子节点指向删除节点的左子节点,
else {
const subsequent = getSubsequent(current)
if (current === this.root) {
this.root = subsequent
} else if (isLeft) {
parent.left = subsequent
} else {
parent.right = subsequent
}
subsequent.left = current.left
}
}
// 查找当前节点的后继节点
// 使用后继节点来替换删除的节点,并改变节点指向
function getSubsequent(node) {
// 保存后继节点、后继节点的父节点
let subsequentParent
let subsequent = node
let current = node.right
while (current !== null) {
subsequentParent = subsequent
subsequent = current
current = current.left
}
// 如果查找的后继节点不是需要删除节点的右节点
if (subsequent !== node.right) {
// 将后继节点的父节点的左子节点指向后继节点的右子节点
subsequentParent.left = subsequent.right
// 将后继节点的右子节点指向删除节点的右子节点
subsequent.right = node.right
}
return subsequent
}
这里称替换节点为删除节点的后继节点,在找到后继节点后,还需要去改变后继节点和后继节点父节点的指向。
说完了删除节点,最后就是获取最大最小值节点,这个比较简单,其实就是遍历整个节点就可以了。代码也非常简单:
BST.prototype.min = function() {
let node = this.root
while (true) {
node = node.left
if (node.left === null) {
return node.data
}
}
}
BST.prototype.max = function() {
let node = this.root
let parent
while (node !== null) {
parent = node
node = node.right
}
return parent.data
}
图
图可以理解为树的一般形式,树其实是一种特殊的图。图就是由顶点和边组成的一种关系。先来看一组术语,了解图的一些概念:
- 顶点,图中的节点
- 度(相邻顶点的数量)
- 路径,几个顶点连接在一起构成的边
- 简单路径(不重复的路径)
- 回路(终点和起点一致的路径
- 无向图
- 有向图(节点路径带有方向的图)
- 无权图
- 带权图(节点带有权重的图)
图的边的表示方法有两种:
- 邻接表
- 邻接矩阵
这里我们采用的是邻接表的方法来表示图,所谓邻接表大概就是这样一种表示方法
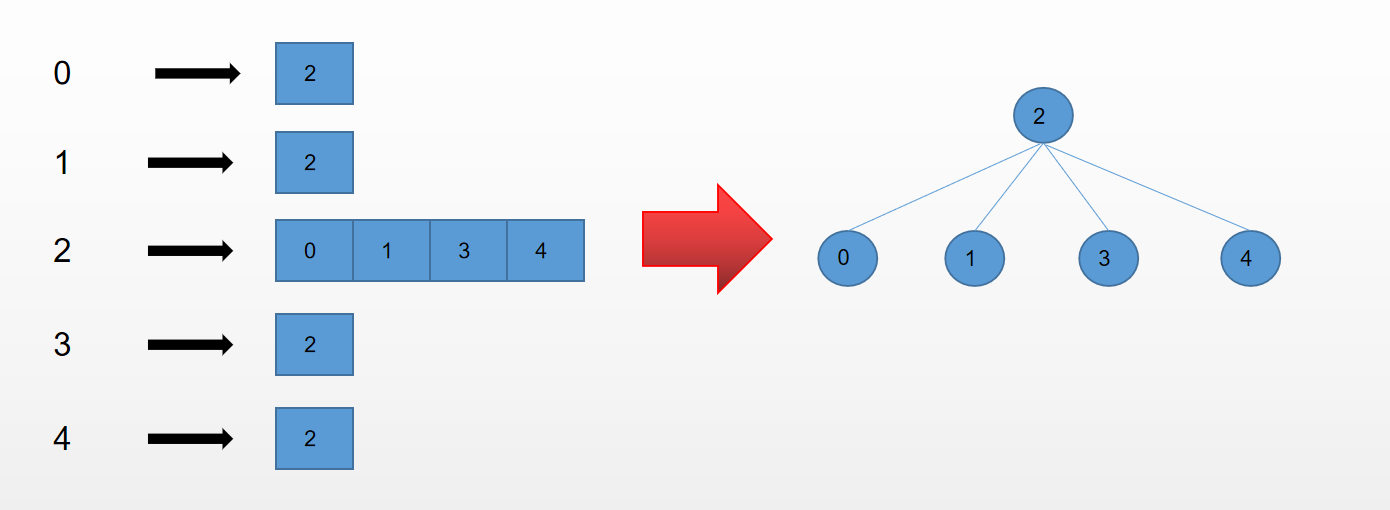
用邻接表来表示的话,就是某个顶点关联了和他相邻的其他顶点,实际就是我们上面的右图组成的一个图。我们用一个Map结构来保存我们的边的信息,键保存顶点,值保存和这个顶点相邻的其他顶点,代码实现如下:
function Graph() {
this.vertexes = []
this.edges = new Map()
// 标记访问过的顶点
this.marked = []
// 初始化所有顶点标记为未访问
for (let i = 0; i < this.vertexes.length; i++) {
this.marked[this.vertexes[i]] = false
}
}
// 添加顶点
Graph.prototype.addVertexes = function(v) {
this.vertexes.push(v)
// 初始化边为空数组
this.edges.set(v, [])
}
// 添加边
Graph.prototype.addEdges = function(v1, v2) {
this.edges.get(v1).push(v2)
this.edges.get(v2).push(v1)
}
Graph.prototype.toString = function() {
let ret = ''
for (let i = 0; i < this.vertexes.length; i++) {
ret += this.vertexes[i] + '->'
const edges = this.edges.get(this.vertexes[i])
for (let j = 0; j < edges.length; j++) {
ret += edges[j] + ' '
}
ret += '\n'
}
return ret
}
图的另外一个重点则是图的两种遍历:
- 广度优先搜索BFS(Breadth-First-Search)
- 深度优先搜索DFS(Depth-First-Search)
广度优先遍历先去遍历初始的节点,然后遍历初始节点的所有其他相邻的节点,将访问过的节点标记为 true,而深度优先遍历则是运用到了递归,先遍历初始节点,再去递归遍历初始节点没有访问过的其他节点。
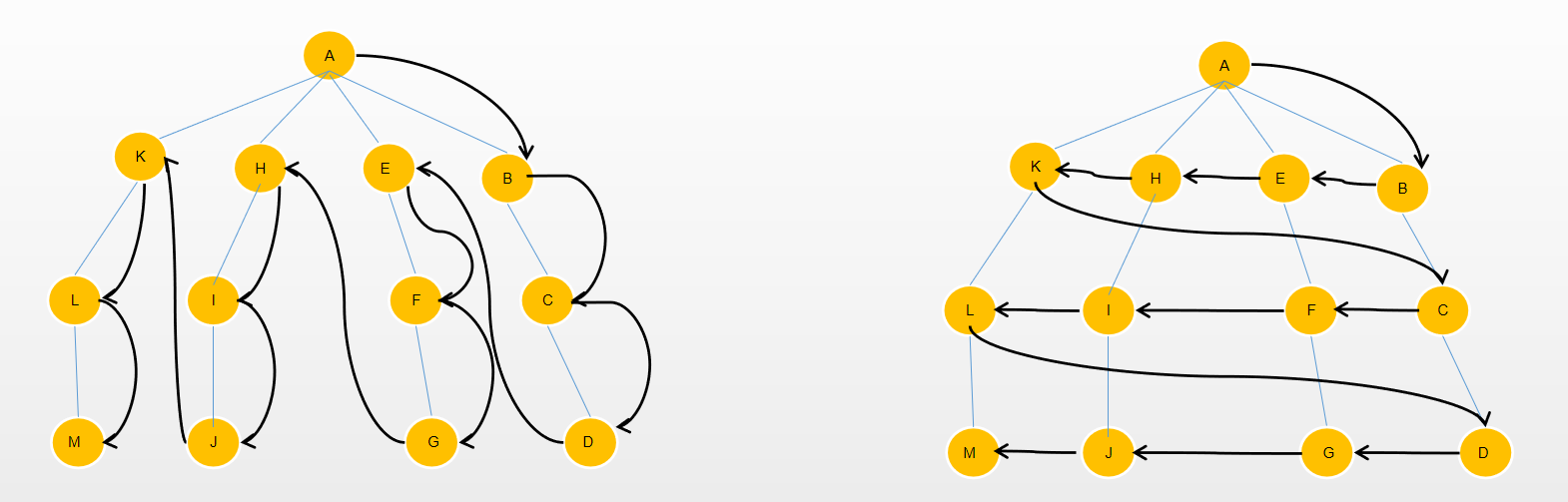
// bfs
Graph.prototype.bfs = function(s) {
let queue = []
this.marked[s] = true
queue.push(s)
while(queue.length > 0) {
const v = queue.shift()
const edges = this.edges.get(v)
if (edges !== undefined) {
console.log('Visited vertex: ' + v)
}
for (let i = 0; i < edges.length; i++) {
if (!this.marked[edges[i]]) {
this.marked[edges[i]] = true
queue.push(edges[i])
}
}
}
}
// dfs
Graph.prototype.dfs = function(s) {
this.marked[s] = true
const edges = this.edges.get(s)
if (edges !== undefined) {
console.log('Visited vertex: ' + s)
}
for (let i = 0; i < edges.length; i++) {
if (!this.marked[edges[i]]) {
this.dfs(edges[i])
}
}
}
算法
在说具体的算法之前,先简单说下时间复杂度,时间复杂度是用来衡量算法执行效率,一般说一个算法的复杂度低,默认说的就是时间复杂度。另外还有空间复杂度也是衡量算法的指标之一,不过更多情况下,依然以时间复杂度为准。需要注意时间复杂度并不是指算法的执行花费时间,而是指算法所花费执行时间的趋势,所以我们看到的算法时间复杂度,其实是执行执行去除系数,最低次幂,常数项等得到的一个值,一般用大O表示法来说明算法的时间复杂度。
排序算法
- 冒泡排序
/**
* 冒泡排序
* 时间复杂度:O(n^2)
*/
function bubleSort(arr) {
const len = arr.length
// 两两比较,因此数组长度最低为2,外层循环比较次数为len - 1
for (let i = len; i >= 2; i--) {
// 每次排序之后,获得最右边的值,下次排序比较次数-1,因此j < i -1
for (let j = 0; j < i - 1; j++) {
if (arr[j] > arr[j + 1]) {
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]
}
}
}
return arr
}
冒泡排序就是数组中的元素两两进行比较,如果后面的值大于前面的值的话,则交换位置。外层循环控制遍历数组的次数,内层循环每次结束后,较大的值则会往右边排列,所以每次内层循环的次数也会减少1。用一个具体的例子来展示上面排序的执行过程:
const arr = [8, 9, 12, 5, 7, 3, 10]
// 第一轮循环后,arr顺序变成这样 [8, 9, 5, 7, 3, 10, 12]
// 第二轮循环后,arr顺序变成这样 [8, 5, 7, 3, 9, 10, 12]
// 第三轮循环后,arr顺序变成这样 [5, 7, 3, 8, 9, 10, 12]
// 第四轮循环后,arr顺序变成这样 [7, 3, 5, 8, 9, 10, 12]
// 第五轮循环后,arr顺序变成这样 [3, 5, 7, 8, 9, 10, 12]
// 所以排序后的arr就变成了[3, 5, 7, 8, 9, 10, 12]
- 选择排序
/**
* 选择排序
* 时间复杂度:O(n^2)
* 交换次数小于冒泡排序
*/
function selectSort(arr) {
const len = arr.length
// 取第一个值和剩下所有的值进行比较,最后一个值不需要和其他值比较,因此外层循环次数为len - 1
for (let i = 0; i < len - 1; i++) {
// 内层循环每次获得左边最小值,每次比较i和i+1后面的所有值
for (let j = i + 1; j < len; j++) {
if (arr[i] > arr[j]) {
[arr[i], arr[j]] = [arr[j], arr[i]]
}
}
}
return arr
}
选择排序则是依次从数组中取出一个值,然后和数组中剩下的值进行比较,最后一个值不需要和其他的值比较,因为最后一个值其实已经比较过了,因此外层循环的次数是len-1。每次外层循环后,会得到一个左边较小的值。还是以上面数组的例子展示一下选择排序的排序过程:
const arr = [8, 9, 12, 5, 7, 3, 10]
// 先使用8和9进行比较,然后8再和12比较,以此类推
// 第一轮循环后,arr顺序变成这样 [3, 9, 12, 8, 7, 5, 10]
// 第二轮循环后,arr顺序变成这样 [3, 5, 12, 9, 8, 7, 10]
// 第三轮循环后,arr顺序变成这样 [3, 5, 7, 12, 9, 8, 10]
// 第四轮循环后,arr顺序变成这样 [3, 5, 7, 8, 12, 9, 10]
// 第五轮循环后,arr顺序变成这样 [3, 5, 7, 8, 9, 12, 10]
// 第六轮循环后,arr顺序变成这样 [3, 5, 7, 8, 9, 10, 12]
// 所以排序后的arr就变成了[3, 5, 7, 8, 9, 10, 12]
- 插入排序
/**
* 插入排序
* 时间复杂度: O(n^2)
* 相对于冒泡排序和选择排序效率更高
*/
function insertSort(arr) {
const len = arr.length
// 比较每项的数值和他左边已排序的树进行比较,外层排序次数len - 1
for (let i = 0; i < len - 1; i++) {
// 内层排序从1开始,和他左边的值进行比较
for (let j = i + 1; j > 0; j--) {
if (arr[j - 1] > arr[j]) {
[arr[j - 1], arr[j]] = [arr[j], arr[j - 1]]
}
}
}
return arr
}
插入排序和冒泡排序类似,都是相邻两个元素进行比较,不同是插入排序是元素和他左边已经排序好的元素进行比较,所以相对于以上两种排序算法,效率会高一点。还是来看看插入排序的执行过程:
const arr = [8, 9, 12, 5, 7, 3, 10]
// 先使用9和8比较,8当做已经排序好的元素,第一次已排序好的只有8,然后以此类推
// 第一、二轮循环后,顺序不变,所以arr顺序还是这样 [8, 9, 12, 5, 7, 3, 10]
// 第三轮循环后,arr顺序变成这样 [5, 8, 9, 12, 7, 3, 10]
// 第四轮循环后,arr顺序变成这样 [5, 7, 8, 9, 12, 3, 10]
// 第五轮循环后,arr顺序变成这样 [3, 5, 7, 8, 9, 12, 10]
// 第六轮循环后,arr顺序变成这样 [3, 5, 7, 8, 9, 10, 12]
// 所以排序后的arr就变成了[3, 5, 7, 8, 9, 10, 12]
- 希尔排序
/**
* 希尔排序
* 多数情况下效率高于简单排序,最坏情况下的时间复杂度为O(n^2)
*/
function shellSort(arr, gap) {
const len = arr.length
for (let i = 0; i < gap.length; i++) {
const n = gap[i]
for (let j = i + n; j < len; j++) {
for (let k = j; k > 0; k -= n) {
if (arr[k] < arr[k - n]) {
[arr[k], arr[k - n]] = [arr[k - n], arr[k]]
}
}
}
}
return arr
}
// 动态计算间隔序列
function shellSort1(arr) {
const len = arr.length
let h = 1
while (h < len / 3) {
h = h * 3 + 1
}
while (h >= 1) {
for (let i = h; i < len; i++) {
for (j = i; j >= h; j -= h) {
if (arr[j] < arr[j - h]) {
[arr[j], arr[j - h]] = [arr[j - h], arr[j]]
}
}
}
h = (h - 1) / 3
}
return arr
}
希尔排序就是以一个间隔来两两比较大小,如下图
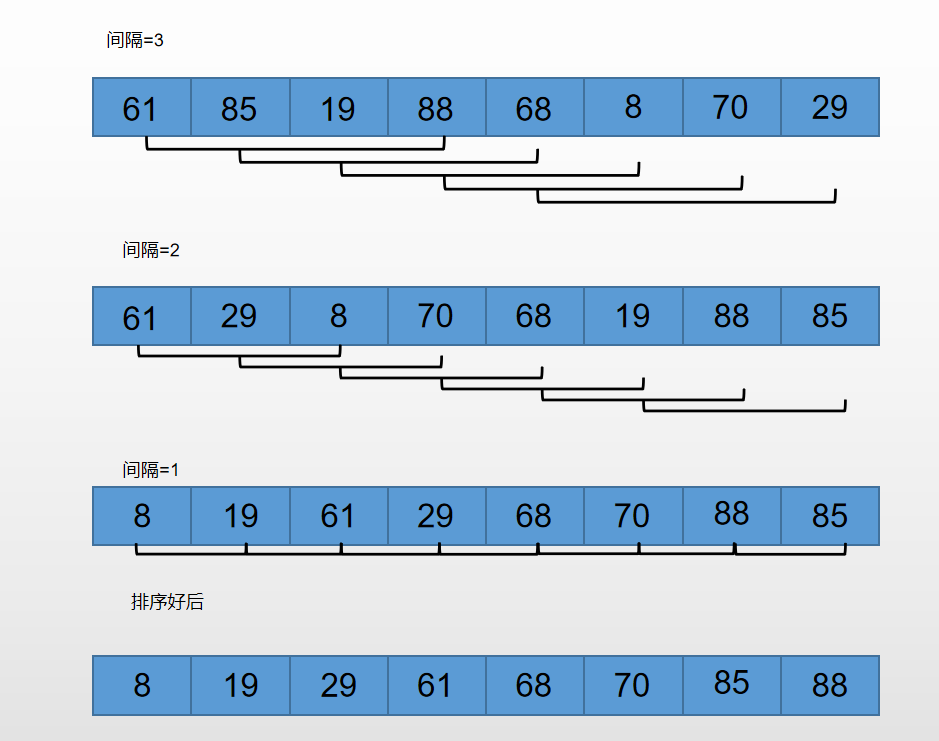
- 快速排序
/**
* 快速排序
* 多数情况下效率最高的
* 时间复杂度:O(nlogn)
*/
function quickSort(arr) {
const len = arr.length
if (len === 0) return []
// 枢纽的选择会影响快速排序的效率
const pivot = arr[0]
const left = []
const right = []
for (let i = 1; i < len; i++) {
if (arr[i] < pivot) {
left.push(arr[i])
} else {
right.push(arr[i])
}
}
return quickSort(left).concat(pivot, quickSort(right))
}
快速排序的思路相较于上面几种排序算法,算是非常容易理解的,就是在数组中找一个值(注意,其实这个值的选择也会影响到快速排序的效劳),然后根据这个值将数组拆分为两个部分,再分别对这两个数组执行递归操作,最后得到的就是我们排序后的结果。
动态规划
动态规划简单来说的话,就是将一个问题分解为若干个相关的部分,通过求出每个部分的最优解,从而得到整个问题的最优解。动态规划和递归不同,递归是通过结论,反推初始的原因,而动态规划则是从底部开始,一层层分解问题,求得部分的问题的解,最终得到最终答案。
下面的斐波那契数列就是一个比较典型的动态规划的例子,如果通过递归来解决问题的话,也非常容易得到下面的代码:
function fibo(n) {
if (n === 1 || n === 2) return 1
return fibo(n - 1) + fibo(n - 2)
}
如果n越来越大的话,则这个算法的效率也会越来越低,并且当n超过某个值后,在node上运行会导致堆栈溢出,原因就是次算法保存了非常多的调用栈。但是仔细分析之后会发现,递归的时候,重复计算了很多次,如果我们将这些计算过的值保存下来,放到下一次的运算中,那么算法的效率就会提升很多。
下面就是斐波那契数列的优化算法:
/**
* 动态规划
* 斐波那契数列的优化
*/
function dynFib(n) {
const val = []
for (let i = 0; i <= n; i++) {
val[i] = []
}
if (n === 1 || n === 2) {
return 1
} else {
val[1] = 1
val[2] = 1
for (let i = 3; i <= n; i++) {
val[i] = val[i - 1] + val[i - 2]
}
return val[n - 1]
}
}
可以看到这次就是将计算过的值保存在了 val 的数组中,这样下次计算从数组中直接取,效率就大大的提升了。
贪心算法
首先得先分析问题是否可以用贪心算法解决,一般来说就是问题无法求得最优解,或者是求得最优解的过程复杂,成本过高。另外则是需要分析能否将整个问题分解为一个个的子问题,并且在只考虑当前子问题的情况下求的解,能否推导或堆叠出全局的解,这才能下结论,说这个问题可以用贪心算法来解决。来看一个著名的背包问题:
现在有四种物品,重量分别为5,20,10,12,他们的价值分别为50,140,60,80,现有一个容量为30的背包,问如何取物品,使得背包中物品的价值最大
/**
* 贪心算法
* 背包问题
*/
function ksack(values, weights, capacity) {
// 初始化剩余容量,物品数量,装入背包的物品价值
let load = 0, i = 0, w = 0
while (load < capacity && i < 4) {
if (weights[i] <= (capacity - load)) {
w += values[i]
load += weights[i]
} else {
// 如果当前物品容量大于背包剩余容量
// 计算背包剩余容量和当前物品容量的比率
// 物品总价值加上当前物品的价值乘以容量比率
let r = (capacity - load) / weights[i]
w += r * values[i]
load += weights[i]
}
i++
}
return w
}
每选择一次物品的时候,如果背包容量能够放下当前物品,则放入物品,如果放不下的话,则计算容量价值比,根据比例加上相对应的价值。
结语
关于数据结构和算法,其实细分还有很多种,本文只是抛砖引玉,也是笔者的学习数据结构算法的入门,有兴趣可以一起研究呀,也欢迎指点纠正。
参考
- 数据结构与算法javascript描述
- javascript数据结构与算法
- 数据结构与算法