为什么要学习数据结构与算法

什么是数据结构？什么是算法？

很多写程序的人都听说过一个公式：程序设计 = 数据结构 + 算法。

然而我在工作中根本没用到这些东西，因为我们平时可能更多的是利用别人已经封装好的接口、类库实现业务逻辑，很少需要自己实现数据结构和算法。但是，别人是如何封装的呢？为什么这样设计呢？

所以想要写出高质量的代码，成为一个优秀的开发者，这些是我们必须要掌握的。

作为一个从事iOS开发n年的程序员，在即将步入三十岁的年龄，感受到了深深的危机，因此从这篇文章开始记录我学习数据结构与算法的过程，不再做一个老菜鸟。

数据结构概念

1.数据

数据是信息的载体，在计算机科学中是指所有能输入到计算机中并能被计算机程序识别和处理的符号集合。可以将数据分为两大类：一类是整数、实数等数值数据；另一类是文字、声音、图形和图像等非数值数据。

2.数据元素

数据元素是数据的基本单位，在计算机程序中通常作为一个整体进行考虑和处理。一个数据元素可由若干个数据项组成。

3.数据项

数据项指不可分割的、具有独立意义的最小数据单位，数据项有时也称为字段或域。

4.数据结构

逻辑结构

数据结构是指互相之间存在着一种或多种关系的数据元素的集合。在任何问题中，数据元素都不会是孤立的，在它们之间存在着这样或那样的关系，这种数据元素之间存在的关系称为数据的逻辑结构。根据数据元素之间关系的不同特性，通常有以下4类基本的逻辑结构。

1、集合结构：在集合结构中，数据元素之间的关系是“属于同一个集合”。数据元素之间除了同属一个集合外，不存在其他关系。
2、线性结构：在该结构中，数据元素除了同属于一个集合外，数据元素之间还存在着一对一的顺序关系。
3、树形结构：该结构的数据元素之间存在着一对多的层次关系。
4、图状结构：该结构的数据元素之间存在着多对多的任意关系，图状结构也称为网状结构。

物理结构

数据结构包括数据的逻辑结构和物理结构。数据的逻辑结构可以看做从具体问题抽象出来的数学模型，它与数据的存储无关。数据的逻辑结构在计算机中的存储表示称为数据的物理结构（或称存储结构），它所研究的是数据结构在计算机中的实现方法，包括数据结构中数据元素的存储表示及数据元素之间关系的表示。在计算机中，数据的存储方法包括顺序存储和链式存储。

顺序存储方法通过数据元素在计算机中存储位置关系来表示元素间的逻辑关系，通常把逻辑上相邻的元素存储在物理位置相邻的存储单元中。顺序存储是一种最基本的存储表示方法，通常借助程序设计语言中的数组来实现。
链式存储方法对逻辑上相邻的元素不要求其物理位置相邻，元素间的逻辑关系通过指针字段来表示，链式存储结构通常借助程序设计语言中的指针来实现。

除了顺序存储方法和链式存储方法外，有时为了查找方便还采用索引存储方法和散列表（Hash）存储方法。讨论数据结构的目的就是在计算机中实现对数据的操作，因此在讨论数据的组织结构时必然要考虑在该结构上进行的操作（或称运算）。事实上，数据结构是专门研究某一类数据的表示方法及其相关操作实现算法的一门学科。

算法

算法是对特定问题求解步骤的一种描述，是指令的有限序列。其中每一条指令表示一个或多个操作。

算法与数据结构是相辅相成的。解决某一类特定问题的算法可以选定不同的数据结构，而且选择恰当与否直接影响算法的效率。

算法特性

有穷性：一个算法必须在有穷步之后结束，即必须在有限时间内完成。
确定性：算法的每一步必须有确切的定义，无二义性，且在任何条件下算法只有唯一一条执行路径，即对于相同的输入只能得出相同的输出。
可行性：算法中的每一步都可以通过已经实现的基本运算的有限次执行得以实现。
输入：一个算法具有零个或多个输入，这些输入取自特定的数据对象集合。
输出：一个算法具有一个或多个输出，这些输出同输入之间存在某种特定的关系。

算法设计要求

正确性：算法的执行结果应当满足预先规定的功能和性能要求。正确性要求表明算法必须满足实际需求，达到解决实际问题的目标。
可读性：一个算法应当思路清晰、层次分明、简单明了、易读易懂。可读性要求表明算法主要是人与人之间交流解题思路和进行软件设计的工具，因此可读性必须要强。同时一个可读性强的算法，其程序的可维护性、可扩展性都要好得多，因此，许多时候人们往往在一定程度上牺牲效率来提高可读性。
健壮性：当输入不合法数据时，应能适当处理，不至于引起严重后果。健壮性要求表明算法要全面细致地考虑所有可能的边界情况，并对这些边界条件做出完备的处理，尽可能使算法没有意外的情况。
高效性：有效使用存储空间和有较好的时间效率。高效性主要是指时间效率，即解决相同规模的问题时间尽可能短。一般来说，数据结构上的基本操作主要有以下几种。

算法分析

所谓好的算法，除了满足上文提到的几个基本要求外，还必须以较少的时间与空间代价来解决相同规模的问题。因此，一个算法的优劣，可以从该算法在计算机上运行的时间和所占存储空间来衡量和评判。算法分析就是预先分析算法在实际执行时的时空代价指标。

时间复杂度

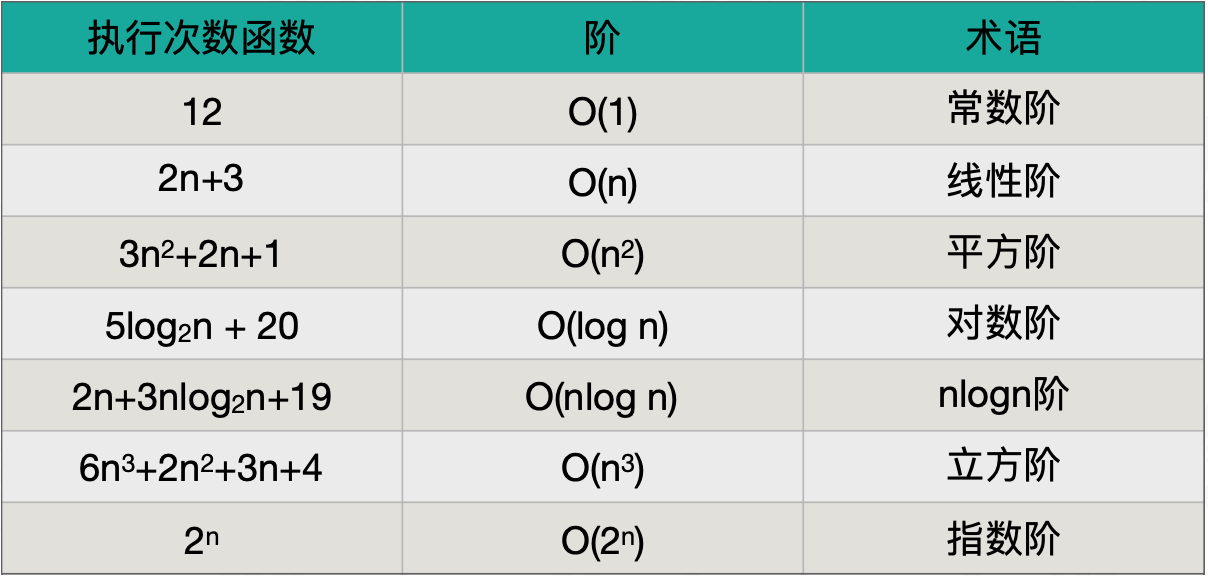
大Ο记号：使用大Ο记号表示的算法的时间复杂度称为算法的渐进时间复杂度。公式：T(n) = O(f(n)) n：表示数据规模的大小； T(n)：表示代码执行的时间； f(n)：表示每行代码执行的次数总和； O：表示代码的执行时间 T(n) 与 f(n) 表达式成正比；

常数阶

//执行2次
 int sum = 0;               
 sum = (1+n)*n/2;

线性阶O(n)

//执行n次 
int sum = 0;               
for (int i = 0; i < n; i++) {
       sum += i;
}

平方阶O(n^2)

//x=x++; 执行n*n次 
 for (int i = 0; i< n; i++) {
        for (int j = 0; j < n ; j++) {
            x=x++;
        }
   }

对数阶O(log n)

//执行log2 n 次
x = 1;
while (x < n)
 x = 2 *x;

立方阶O(log n^3)

//执行n*n*n次
int sum = 1;                       
for (int i = 0; i < n; i++) {       
     for (int j = 0 ; j < n; j++) {   
         for (int k = 0; k < n; k++) { 
             sum = sum * 2;         
         }
     }
 }

nlogn 阶 O(nlog n)

//执行n*log2 n 次
count = 0;
for(k=1;k<=n;k*=2){
   for(j=1;j<n;j++){
      count++
  }
}

空间复杂度

一个程序的空间复杂度是指程序运行从开始到结束所需的存储量与问题规模的对应关系，记做： S(n)=Ο(f(n)) 其中n为问题的规模（或大小）。一个上机执行的程序除了需要存储空间来寄存本身所用指令、常数、变量和输入数据外，还需要一些对数据进行操作的工作单元和存储为实现计算所需信息的辅助空间。若输入数据所占空间只取决于问题本身、和算法无关，则只需分析除输入数据和程序之外的额外空间，否则应同时考虑输入数据本身所需空间（和输入数据的表示形式有关）。若额外空间相对于输入数据量来说是常数，则称此算法为原地工作，辅助空间为Ο(1)。如果所占空间量依赖于特定的输入，则除特别指明外，均按最坏情况来分析。算法执行时间的耗费和所占存储空间的耗费是相互矛盾的，难以兼得。即算法执行时间上的节省是以增加存储空间为代价的，反之亦然。不过，一般而言，常常已以算法执行时间作为算法优劣的主要衡量指标。

数据结构与算法（一）：基本概念