内容介绍

快速排序简介
快速排序(Quicksort)是对冒泡排序的一种改进。快速排序由C. A. R. Hoare在1960年提出。快速排序算法被列为20世纪十大算法之一,这足以说明的他的作用和重要性。快速排序是程序员必须掌握的一种排序算法。
希尔排序相当于直接插入排序的升级,它们同属于插入排序类,快速排序其实就是我们前面认为最慢的冒泡排序的升级,它们都属于交换排序类。它也是通过不断比较和移动交换来实现排序的,只不过它的实现,增大了记录的比较和移动的距离,快速排序会取一个分界值,将比分界值大的记录从前面直接移动到后面,比分界值小的记录从后面直接移动到前面,从而减少了总的比较次数和移动交换次数。
快速排序的思想
快速排序的思想:取一个分界值,通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比分界值小,另外一部分的所有数据比分界值大,然后再按此方法对这两部分数据分别进行相同操作,整个排序过程可以递归进行,最终达到整个数据变成有序序列。


快速排序动画演示
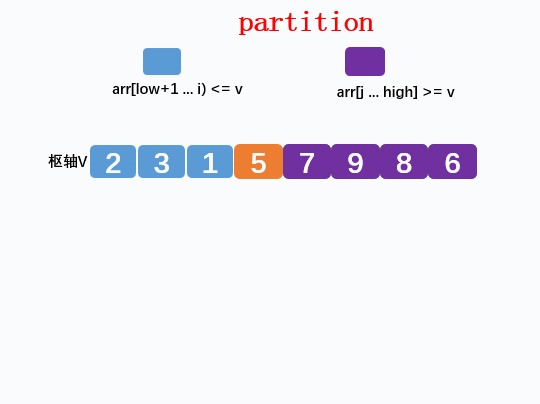
快速排序分析
一般没有特殊要求排序算法都是升序排序,小的在前,大的在后。
数组由{5, 3, 1, 9, 7, 2, 8, 6} 这8个无序元素组成。
快速排序步骤:
取一个分界值:我们暂且拿待排序数据的最前一个元素作为分界值(枢轴)。

分区,low到high之间的元素分成左边小于枢轴,最右边大于枢轴。

分区后小于枢轴和大于枢轴的两个区域再进行分区,依次类推直到每个分区数据满足左边小于枢轴,右边大于枢轴,排序完成。
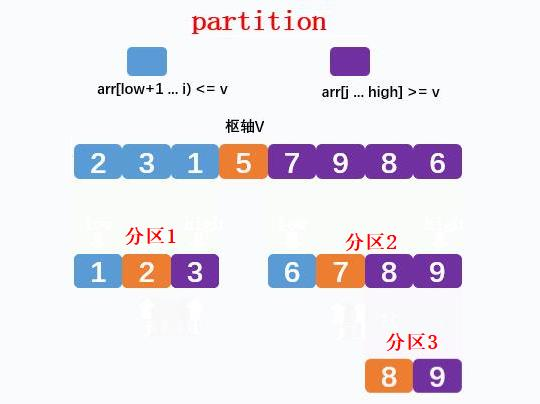
最终结果,如下图:

快速排序需要解决的两个问题:
- 分区后还需要分区可以使用递归。
- 分区时如何让小于枢轴的数据放到枢轴左边,大于枢轴的数据放到枢轴的右边。
使用两个指针(i,j),i是用来找小于枢轴的数据,j是用来找大于枢轴的数据。
i. 循环查找到需要换位置的数据,进行换位置。
ii. 当i索引的数据大于枢轴,这个数据需要换位置,记录i的值,停止查找。
iii. 当j索引的数据小于枢轴,这个数据需要换位置,记录j的值,停止查找。
iv. 如果i > j说明已经找完了,退出循环。
v. 让i和j位置的元素换位置,i++,指针向右移动继续找大于枢轴的数据,j--向左移动继续找小于枢轴的数据。过程如下动画所示: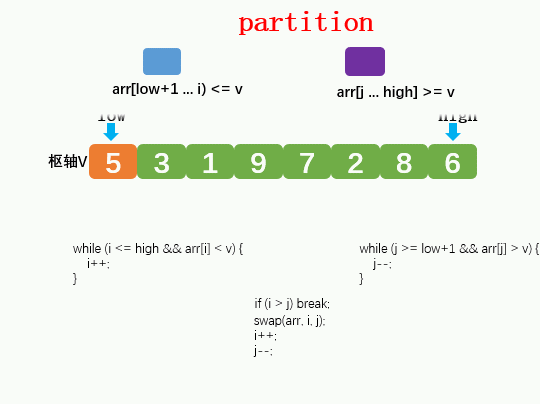
快速排序代码编写
代码说明:
void quickSort(int[] arr)方法:用于快速排序的方法,参数为需要排序的数组。void qSort(int[] arr, int low, int high)方法:用于将数组指定范围的数据进行快速排序,此方法不暴露给用户使用。int partition(int[] arr, int low, int high)方法:快速排序的分区,将low到high之间的元素分成左边小于枢轴,最右边大于枢轴,返回枢轴的位置。void swap(int[] arr, int start, int end)方法:将arr数组start索引和end索引的元素进行交换位置。
快速排序代码如下:
public class QuickSortTest {
public static void main(String[] args) {
int[] arr = new int[] {5, 3, 1, 9, 7, 2, 8, 6};
quickSort(arr);
System.out.println("排序后:" + Arrays.toString(arr));
}
public static void quickSort(int[] arr) {
qSort(arr, 0, arr.length-1);
}
// 对arr数组的[low, right]部分进行快速排序
private static void qSort(int[] arr, int low, int high) {
if (low >= high) return;
// 快速排序的分区,将low到high之间的元素分成左边小于枢轴,最右边大于枢轴
int pivot = partition(arr, low, high);
// 再次对枢轴左边和右边的数据进行分区。
qSort(arr, low, pivot - 1);
qSort(arr,pivot + 1, high);
}
// 快速排序的分区,将low到high之间的元素分成左边小于枢轴,最右边大于枢轴,返回枢轴的位置。
private static int partition(int[] arr, int low, int high) {
// 将第一个元素作为枢轴
int v = arr[low];
int i = low + 1; // arr[low+1, i) <= v; arr(j, high] >= v
int j = high;
while (true) {
// 从左边找到大于枢轴的数据
while (i <= high && arr[i] < v) {
i++;
}
// 从右边找到小于枢轴的数据
while (j >= low+1 && arr[j] > v) {
j--;
}
if (i > j) break;
swap(arr, i, j); // 交换i和j位置的元素
i++; // 左边的指针向右移动继续找大于枢轴的数据
j--; // 右边的指针向左移动继续找小于枢轴的数据
}
// 交换枢轴到j索引,保证枢轴左边的元素小于枢轴,枢轴右边元素大于枢轴。
swap(arr, low, j);
return j;
}
// 数组两个元素交换
public static void swap(int[] arr, int start, int end) {
if (start == end)
return;
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
}
}
快速排序代码优化1
优化枢轴的选取
我们知道快速会不断对数据进行分区,选定一个枢轴,将小于枢轴的数据放到左边,大于枢轴的数据放到右边。
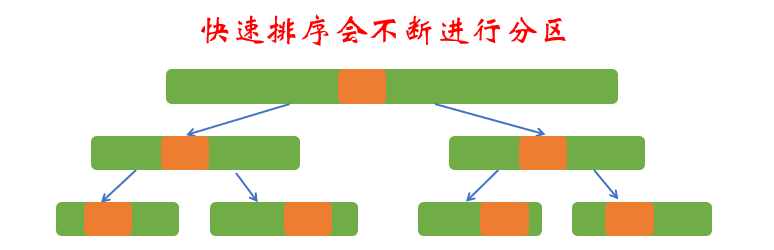
前面我们在对数据进行分区时,都是以数组最前面一个元素作为枢轴,枢轴的选取不够合理。这样会存在一个问题,当数据本身近乎有序时比如数据为:{1, 2, 3, 5, 6, 7, 9, 8},分区时选择最左边的数据作为枢轴,恰好是数组最小或最大数据,导致分区时,数据都在数轴一侧会导致快速排序退化为一个O(n2)的算法。

如何选取枢轴才不会让近乎有序的数据排序退化成O(n^2)呢,我们可以看到原因是我们一直选取数组最前面的一个数据作为枢轴,因此我们可以随机选取一个元素作为数轴,这样,每次都选取到最大或最小的概率就会非常低。改进后的代码如下:
public class QuickSortTest2 {
public static void main(String[] args) {
int[] arr = new int[] {5, 3, 1, 9, 7, 2, 8, 6};
quickSort(arr);
System.out.println("排序后:" + Arrays.toString(arr));
}
public static void quickSort(int[] arr) {
qSort(arr, 0, arr.length-1);
}
// 对arr数组的[low, right]部分进行快速排序
public static void qSort(int[] arr, int low, int high) {
if (low >= high) return;
// 快速排序的分区,将low到high之间的元素分成左边小于枢轴,最右边大于枢轴
int pivot = partition2(arr, low, high);
// 再次对枢轴左边和右边的数据进行分区。
qSort(arr, low, pivot - 1);
qSort(arr,pivot + 1, high);
}
// 数组两个元素交换
public static void swap(int[] arr, int start, int end) {
if (start == end)
return;
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
}
// 快速排序的分区,将low到high之间的元素分成左边小于枢轴,最右边大于枢轴,返回枢轴的位置。
private static int partition2(int[] arr, int low, int high) {
// 将第一个元素作为枢轴,如果数组是近乎有序的数组,那么每次使用第一个元素拆分,会让拆分倾斜到一边,非常的不平衡.
// 修改成随机选取一个元素作为数轴
Random ran = new Random();
// 得到随机的索引
int rIndex = ran.nextInt(10000000) % (high - low + 1) + low;
// 拿这个随机索引的数据和最前面的数据交换,这个随机的数据作为数轴
swap(arr, low, rIndex);
// 将第一个元素作为枢轴
int v = arr[low];
int i = low + 1; // arr[low+1, i) <= v; arr(j, high] >= v
int j = high;
while (true) {
// 从左边找到大于枢轴的数据
while (i <= high && arr[i] < v) {
i++;
}
// 从右边找到小于枢轴的数据
while (j >= low+1 && arr[j] > v) {
j--;
}
if (i > j) break;
swap(arr, i, j); // 交换i和j位置的元素
i++; // 左边的指针向右移动继续找大于枢轴的数据
j--; // 右边的指针向左移动继续找小于枢轴的数据
}
// 交换枢轴到j索引,保证枢轴左边的元素小于枢轴,枢轴右边元素大于枢轴。
swap(arr, low, j);
return j;
}
}
快速排序代码优化2
小数据量使用插入排序
现在我们的快速排序是一直分区,直到分区中的每个元素都有序,我们知道插入排序在数据量小时效率相对较高,当元素数量较少时,我们可以使用插入排序来替换继续分区,从而提高插入排序的效率,优化后代码如下:
public class QuickSortTest3 {
public static void main(String[] args) {
int[] arr = new int[] {5, 3, 1, 9, 7, 2, 8, 6};
quickSort(arr);
System.out.println("排序后:" + Arrays.toString(arr));
}
public static void quickSort(int[] arr) {
qSort(arr, 0, arr.length-1);
}
// 对arr数组的[low, right]部分进行快速排序
public static void qSort(int[] arr, int low, int high) {
if (low >= high) return;
if (high - low <= 15) {
insertionSort(arr, low, high);
return;
}
// 快速排序的分区,将low到high之间的元素分成左边小于枢轴,最右边大于枢轴
int pivot = partition2(arr, low, high);
// 再次对枢轴左边和右边的数据进行分区。
qSort(arr, low, pivot - 1);
qSort(arr,pivot + 1, high);
}
// 对数组指定索引范围的元素使用插入排序
public static void insertionSort(int[] arr, int low, int high) {
for (int i = low + 1; i <= high; i++) {
int e = arr[i]; // 得到当前这个要插入的元素
int j;
for (j = i; j > low && arr[j-1] > e; j--) {
arr[j] = arr[j-1];
}
arr[j] = e;
}
}
// 快速排序的分区,将low到high之间的元素分成左边小于枢轴,最右边大于枢轴,返回枢轴的位置。
private static int partition2(int[] arr, int low, int high) {
// 将第一个元素作为枢轴,如果数组是近乎有序的数组,那么每次使用第一个元素拆分,会让拆分倾斜到一边,非常的不平衡.
// 修改成随机选取一个元素作为数轴
Random ran = new Random();
// 得到随机的索引
int rIndex = ran.nextInt(10000000) % (high - low + 1) + low;
// 拿这个随机索引的数据和最前面的数据交换,这个随机的数据作为数轴
swap(arr, low, rIndex);
// 将第一个元素作为枢轴
int v = arr[low];
int i = low + 1; // arr[low+1, i) <= v; arr(j, high] >= v
int j = high;
while (true) {
// 从左边找到大于枢轴的数据
while (i <= high && arr[i] < v) {
i++;
}
// 从右边找到小于枢轴的数据
while (j >= low+1 && arr[j] > v) {
j--;
}
if (i > j) break;
swap(arr, i, j); // 交换i和j位置的元素
i++; // 左边的指针向右移动继续找大于枢轴的数据
j--; // 右边的指针向左移动继续找小于枢轴的数据
}
// 交换枢轴到j索引,保证枢轴左边的元素小于枢轴,枢轴右边元素大于枢轴。
swap(arr, low, j);
return j;
}
// 数组两个元素交换
public static void swap(int[] arr, int start, int end) {
if (start == end)
return;
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
}
}
快速排序代码优化3
3路快速排序
前面我们在进行分区时,大量和枢轴重复的数据还会进入下一次排序。代码如下:
private static int partition2(int[] arr, int low, int high) {
...
while (true) {
// 从左边找到大于枢轴的数据
while (i <= high && arr[i] < v) {
i++;
}
// 从右边找到小于枢轴的数据
while (j >= low+1 && arr[j] > v) {
j--;
}
if (i > j) break;
swap(arr, i, j); // 交换i和j位置的元素
i++; // 左边的指针向右移动继续找大于枢轴的数据
j--; // 右边的指针向左移动继续找小于枢轴的数据
}
...
}
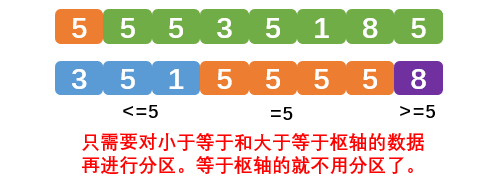
进行一次分区后,大量和枢轴重复的数据还会进入下一次排序,浪费性能,和枢轴相同的数据不用再进入下次分区。效果如下:

因此我们在进行分区时,可以将数据分成3个区域,小于枢轴的数据,等于数轴的数据,大于枢轴的数据,这样处理的好处是等于枢轴的数据不会进入下一次分区,所以在待排序数据中出现大量重复数据时可以提高效率。
优化后代码:
public class QuickSortTest4 {
public static void main(String[] args) {
int[] arr = new int[] {5, 3, 1, 9, 7, 2, 8, 6};
quickSort3Ways(arr);
System.out.println("排序后:" + Arrays.toString(arr));
}
public static void quickSort3Ways(int[] arr) {
qSort3Ways(arr, 0, arr.length-1);
}
// 对arr数组的[low, right]部分进行快速排序
public static void qSort3Ways(int[] arr, int low, int high) {
if (low >= high) return;
if (high - low <= 15) {
insertionSort(arr, low, high);
return;
}
int pivot = partition3Ways(arr, low, high);
qSort3Ways(arr, low, pivot - 1);
qSort3Ways(arr,pivot + 1, high);
}
private static int partition3Ways(int[] arr, int low, int high) {
// 将第一个元素作为枢轴,如果数组是近乎有序的数组,那么每次使用第一个元素拆分,会让拆分倾斜到一边,非常的不平衡.
// 修改成随机选取一个数字进行拆分
Random ran = new Random();
int rIndex = ran.nextInt(10000000) % (high - low + 1) + low;
swap(arr, low, rIndex);
int v = arr[low];
int lt = low; // arr[l+1...lt] < v
int gt = high + 1; // arr[gt...r] > v
int i = low+1; // arr[lt+1...i) == v
while (i < gt) {
if (arr[i] < v) {
swap(arr, i, lt+1);
i++;
lt++;
} else if (arr[i] > v) {
swap(arr, i, gt-1);
gt--;
} else {
i++;
}
}
swap(arr, low, lt);
return lt;
}
// 对数组指定索引范围的元素使用插入排序
public static void insertionSort(int[] arr, int low, int high) {
for (int i = low + 1; i <= high; i++) {
int e = arr[i]; // 得到当前这个要插入的元素
int j;
for (j = i; j > low && arr[j-1] > e; j--) {
arr[j] = arr[j-1];
}
arr[j] = e;
}
}
// 数组两个元素交换
public static void swap(int[] arr, int start, int end) {
if (start == end)
return;
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
}
}
快速排序代码优化4
减少递归次数
我们知道,递归对性能有一定影响,上面的qSort3Ways方法内部先进行分区,然后进行两次递归。如果待排序的序列划分极端不平衡,递归深度将趋近于n,而不是平衡时的log2n, 除了分区次数变多,影响排序效率之外。栈的大小是很有限的,每次递归调用都会耗费一定的栈空间,因此减少递归,可以提高性能,并且防止栈空间不足而导致的栈溢出问题。
减少递归次数后的代码如下:
public class QuickSortTest5 {
public static void main(String[] args) {
int[] arr = new int[] {5, 3, 1, 9, 7, 2, 8, 6};
quickSort3Ways(arr);
System.out.println("排序后:" + Arrays.toString(arr));
System.out.println("我被递归了:" + count);
}
public static void quickSort3Ways(int[] arr) {
qSort3Ways(arr, 0, arr.length-1);
}
private static int count;
// 对arr数组的[low, right]部分进行快速排序
public static void qSort3Ways(int[] arr, int low, int high) {
if (low >= high) return;
count++;
if (high - low <= 15) {
insertionSort(arr, low, high);
} else {
while (low < high) {
int pivot = partition3Ways(arr, low, high);
qSort3Ways(arr, low, pivot - 1);
low = pivot + 1; // 循环会对右边的区域进行分区,而不是递归再对右边进行分区
}
}
}
private static int partition3Ways(int[] arr, int low, int high) {
// 将第一个元素作为枢轴,如果数组是近乎有序的数组,那么每次使用第一个元素拆分,会让拆分倾斜到一边,非常的不平衡.
// 修改成随机选取一个数字进行拆分
Random ran = new Random();
int rIndex = ran.nextInt(10000000) % (high - low + 1) + low;
swap(arr, low, rIndex);
int v = arr[low];
int lt = low; // arr[l+1...lt] < v
int gt = high + 1; // arr[gt...r] > v
int i = low+1; // arr[lt+1...i) == v
while (i < gt) {
if (arr[i] < v) {
swap(arr, i, lt+1);
i++;
lt++;
} else if (arr[i] > v) {
swap(arr, i, gt-1);
gt--;
} else {
i++;
}
}
swap(arr, low, lt);
return lt;
}
// 对数组指定索引范围的元素使用插入排序
public static void insertionSort(int[] arr, int low, int high) {
for (int i = low + 1; i <= high; i++) {
int e = arr[i]; // 得到当前这个要插入的元素
int j;
for (j = i; j > low && arr[j-1] > e; j--) {
arr[j] = arr[j-1];
}
arr[j] = e;
}
}
// 数组两个元素交换
public static void swap(int[] arr, int start, int end) {
if (start == end)
return;
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
}
}
总结
- 快速排序其实就是我们前面认为最慢的冒泡排序的升级,它们都属于交换排序类。
- 快速排序的思想:取一个分界值,通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比分界值小,另外一部分的所有数据比分界值大,然后再按此方法对这两部分数据分别进行相同操作,整个排序过程可以递归进行,最终达到整个数据变成有序序列。
- 快速排序代码优化1:优化枢轴的选取。
- 快速排序代码优化2:小数据量使用插入排序。
- 快速排序代码优化3: 3路快速排序。
- 快速排序代码优化4:减少递归次数。
快速排序算法被列为20世纪十大算法之一,经过多次的优化后,在整体性能上,依然是排序算法王者,快速排序是程序员必须掌握的一种排序算法。

---------- End ----------
原创文章和动画制作真心不易,您的点赞就是最大的支持!
想了解更多文章请关注微信公众号:表哥动画学编程