数据分析小案例：销量预测（python）将数据存储为csv格式，导入python。并画出散点图，观察气温和销售量的关系。

案件

1，现有冰激凌店一年的历史销售数据

2，数据包括单日的销售量、气温、周几（问题：如何用这些数据预测冰激凌的销量？）

模拟实验与分析

将数据存储为csv格式，导入python。并画出散点图，观察气温和销售量的关系。

[Python]

纯文本查看

复制代码

import pandas as pd

icecream = pd.read_csv("icecream.csv")

import matplotlib.pyplot as plt

import pylab

plt.rcParams['font.sans-serif'] = ['SimHei']

plt.scatter(icecream.iloc[:,1],icecream.iloc[:,0])

plt.xlabel("气温")

plt.ylabel("销售量")

pylab.show()

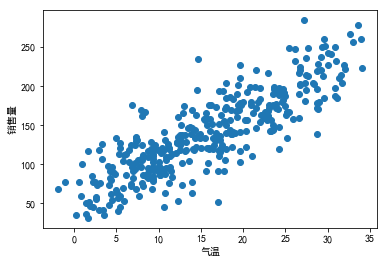
计算两者间的相关系数。

[Python]

纯文本查看

复制代码

1	`icecream.iloc[:,0:2].corr()`

结果为：

[Python]

纯文本查看

复制代码

销售量气温[/align]

销售量 1.000000 0.844211

气温 0.844211 1.000000

销售量和气温的相关系数为0.84，结合散点图，认为两者相关。下面用回归分析的方法，通过气温来预测冰激凌销量。

[Python]

纯文本查看

复制代码

from sklearn.linear_model import LinearRegression

model = LinearRegression()

feature_cols = ['气温']

X = icecream[feature_cols]

y = icecream.销售量

model.fit(X,y)

plt.scatter(icecream.气温, icecream.销售量)

plt.plot(icecream.气温, model.predict(X) , color='blue')

plt.xlabel('气温')

plt.ylabel('销售量')

plt.show()

print("截距与斜率:",model.intercept_,model.coef_)

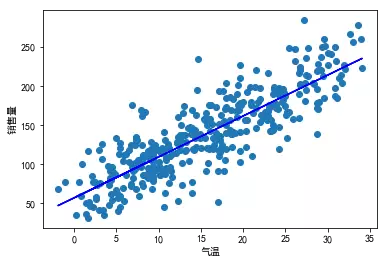
[Python]

纯文本查看

复制代码

1	`截距与斜率:` `57.1673282152` `[` `5.21607823]`

于是，散点图中的线函数式为y＝5.2X＋57.2。所以，当气温为25度时，预测的销售量为5.2*25+57.2=187.52，约188个。
几个小概念回归分析：预测数据时的简便手法。在此例中，销售量为反应变量，也叫因变量，气温为解释变量，也叫自变量。虽然影响销售量的因素除了气温外还有很多，但回归分析中我们要把现实情况简化并公式化，这个过程叫做建模。本例中只用1个解释变量进行模型化称为一元线性回归，如果反应变量同时受到多个解释变量的影响，称为多元线性回归。

更多python学习资料可关注：gzitcast