浅析简易k线图图表
先说下实现的需求: 我们需要一个x轴分为12个刻度,x轴最大值为24. y轴最大刻度值为180,这样的一个k线图,如右图所示

我们先来整理下思路:
x最大为刻度24,y最大值为180.那么我们怎么去绘制x轴刻度呢? 仔细想想,x轴分为12份,最大值24.并且k线图表的宽度是已知的,那么我们等比例计算: xStep(一个刻度)=已知宽度/24。 不就可以知道一个刻度值是多少了么?
那我们再来分析分析y轴的怎么处理。
现在已知的数值:最大值180,图表的高度(ps:别纠结图表高宽怎么来的啊~会挨板子的。控件生命周期onLayout 哪里就可以获取了) 那么 参考x轴的计算方式,一样我们可以通过:yStep=已知高度/180.是不是挺简单的啊。至于驼峰,留到文末再说。有了思路,那么代码实现起来就很容易了,写这篇简易文章的出发点是想跟大家说说自己平常的个人观点,不要什么场景、事物开始前都想着直接找轮子,自己尝试实现、摸索的过程对于个人是y很有益的。咳咳咳,不好意思。我跑题了。 回到原点,接下来开始编码部分:
编写X轴
继承View 重写onLayout 获取已知高宽
@Override
protected void onLayout(boolean changed, int left, int top, int right, int bottom) {
super.onLayout(changed, left, top, right, bottom);
width = getWidth();
height = getHeight();
}
按照上面分析的公式,绘制X轴刻度
xPaint = new Paint();
xPaint.setAntiAlias(true);
xPaint.setStrokeWidth(xlinewidth);
xPaint.setStrokeCap(Paint.Cap.ROUND);
xPaint.setColor(xlinecolor);
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
step = width / 24f;
y_step = height / 180f;
canvas.drawLine(0, height, width, height, xPaint);
for (int i = 0; i <= 12; i++) {
canvas.drawLine((i * 2) * step, 0, (i * 2) * step, height, xPaint);
}
}

知道刻度步伐,实现轴刻度是不是简单多了。 接下来我们绘制k线吧。 我有一个24长度的集合数据:
ArrayList<Integer> data = new ArrayList<>();
data.add(10);
data.add(50);
data.add(100);
data.add(40);
data.add(120);
data.add(60);
data.add(80);
data.add(160);
data.add(90);
data.add(80);
data.add(60);
data.add(40);
data.add(20);
data.add(50);
data.add(80);
data.add(100);
data.add(130);
data.add(160);
data.add(180);
data.add(50);
data.add(120);
data.add(100);
data.add(80);
data.add(60);
data.add(10);
集合的角标分别对应x轴的1-24,我想把他们体现在图标上。那要怎么做呢? 其实想想,我们已知xStep和yStep,那么不久可以知道每个值在每个刻度的x,y坐标了么? 如 data集合0角标:x坐标=xStep1 y坐标=yStep10(data集合0角标的值)。 绘制一个点需要x,y就足够了。 那么我们的实现逻辑代码如下:
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
step = width / 24f;
y_step = height / 180f;
canvas.drawLine(0, height, width, height, xPaint);
for (int i = 0; i <= 12; i++) {
canvas.drawLine((i * 2) * step, 0, (i * 2) * step, height, xPaint);
}
Path path = new Path();
path.moveTo(0, height);
for (int i = 0; i < data.size(); i++) {
float x = (i + 1) * step; //这是x坐标
float y = height - (data.get(i) * y_step);//这是y坐标 总高度-y坐标,是为了从下往上
path.lineTo(x, y);
}
canvas.drawPath(path, linePaint);
}
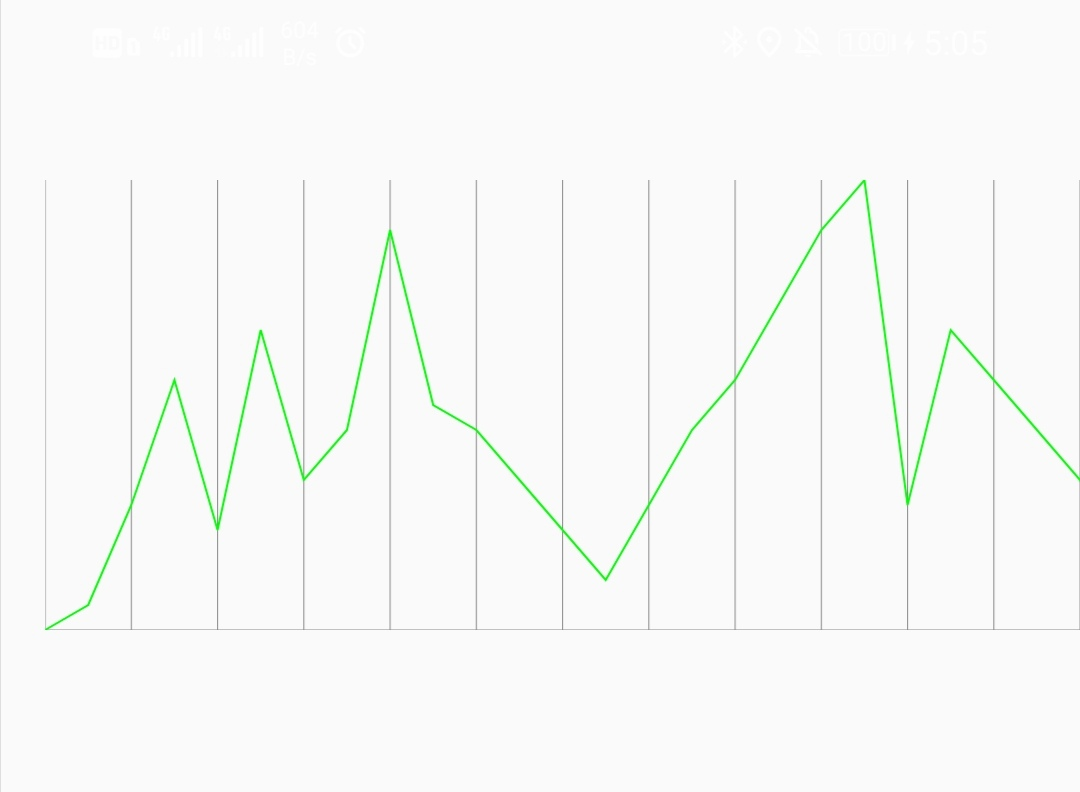
到了这一步是不是感觉特别简单啊,那么恭喜你,又收获了自定义综合使用路上的小小知识点。毕竟水滴石穿嘛。 言归正传,我们还有最后一个步骤,渲染驼峰呢~~~ 这一步我就不罗嗦了,官方其实有提供api的,小火鸡们平常要多查查看看文档啊(LinearGradient)
mPaintShader = new Paint();
mPaintShader.setAntiAlias(true);
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
step = width / 24f;
y_step = height / 180f;
canvas.drawLine(0, height, width, height, xPaint);
for (int i = 0; i <= 12; i++) {
canvas.drawLine((i * 2) * step, 0, (i * 2) * step, height, xPaint);
}
//绘制折线
Path path = new Path();
path.moveTo(0, height);
for (int i = 0; i < data.size(); i++) {
float x = (i + 1) * step; //这是x坐标
float y = height - (data.get(i) * y_step);//这是y坐标 总高度-y坐标,是为了从下往上
path.lineTo(x, y);
}
path.lineTo(width, height);
canvas.drawPath(path, linePaint);
Shader mShader = new LinearGradient(0, height + 10, 0, 0, getResources().getColor(R.color.colorAccent1), getResources().getColor(R.color.colorAccent5), Shader.TileMode.REPEAT);
//新建一个线性渐变,前两个参数是渐变开始的点坐标,第三四个参数是渐变结束的点的坐标。连接这2个点就拉出一条渐变线了,
// 。然后那个数组是渐变的颜色。下一个参数是渐变颜色的分布,如果为空,每个颜色就是均匀分布的。最后是模式,这里设置的是循环渐变
mPaintShader.setShader(mShader);
canvas.drawPath(path, mPaintShader);
}
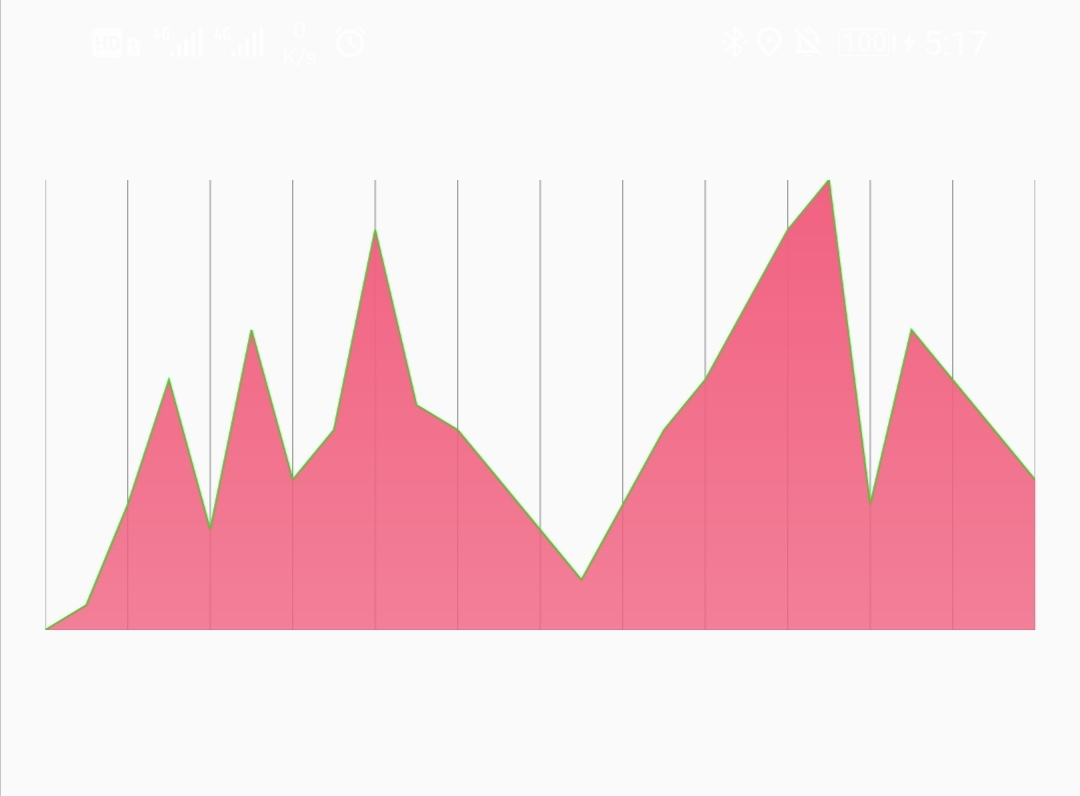
回过头看看,这一切实现起来不麻烦吧,只要平常多分析分析,碰到需求可以适当尝试一下自己实现,毕竟技术进阶之路不是一味的搬轮子~~不喜勿碰