小码哥数据结构与算法(九): AVL树

平克曼
179 阅读9分钟

一、AVL树

  • AVL树是最早发明的自平衡二叉搜索树之一

  • AVL 取名于两位发明者的名字

  • G. M. Adelson-Velsky 和 E. M. Landis（来自苏联的科学家）

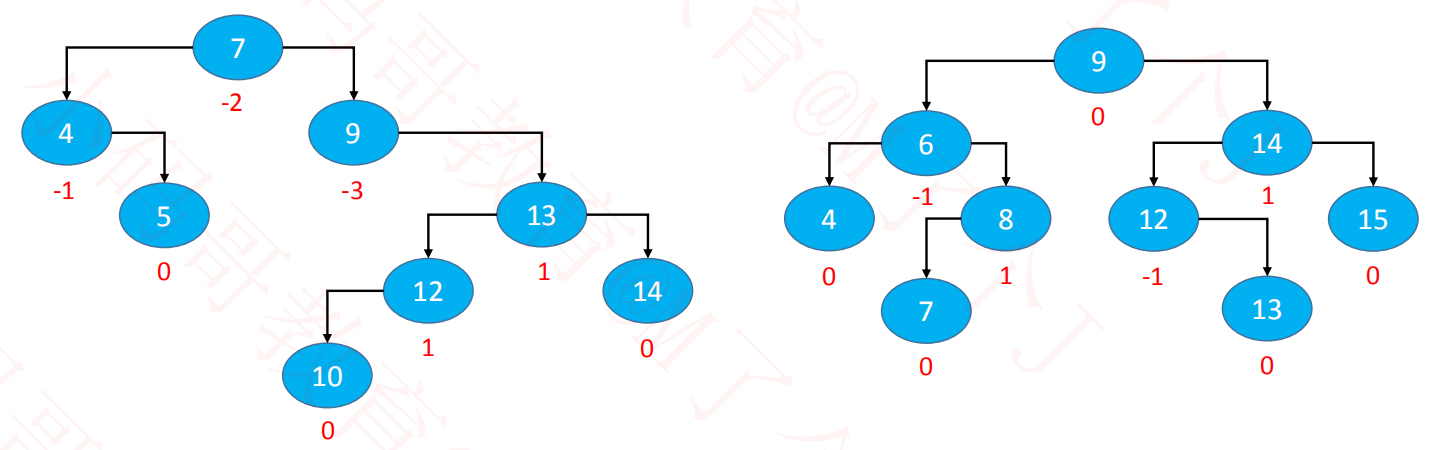
  • 平衡因子（Balance Factor）：某结点的左右子树的高度差

    AVL树的特点

    • 每个节点的平衡因子只可能是 1、0、-1（绝对值 ≤ 1，如果超过 1，称之为“失衡”）

    • 每个节点的左右子树高度差不超过 1

    • 搜索、添加、删除的时间复杂度是 O(logn)

image-20200328003921752

图1-1

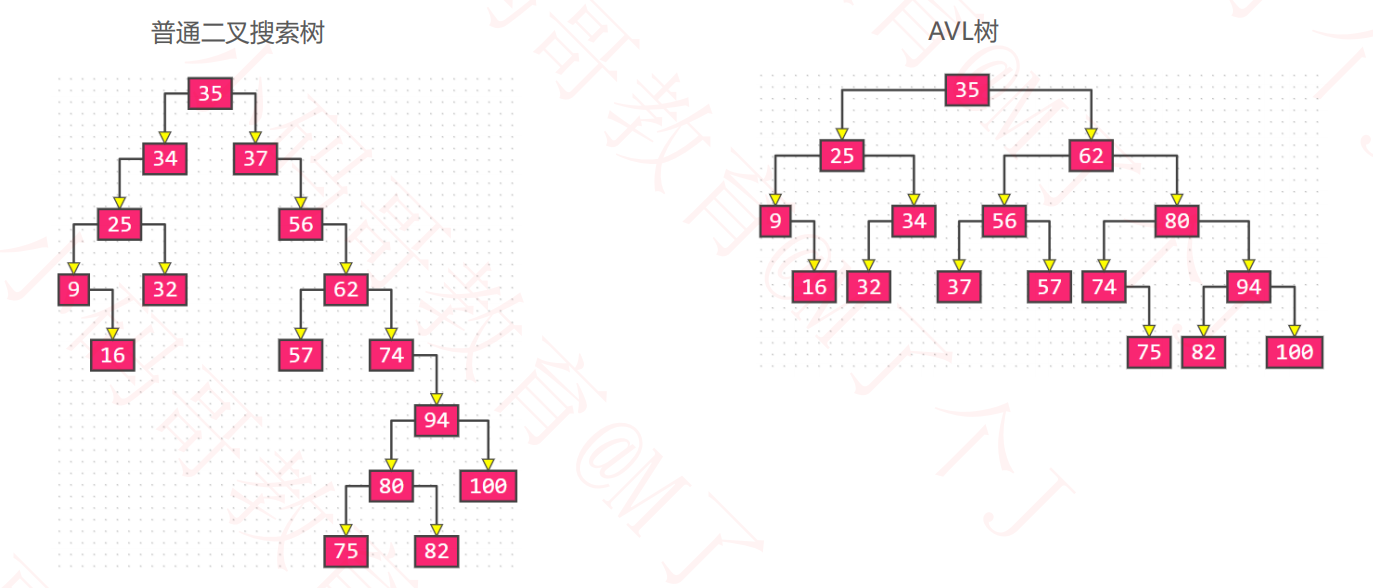
平衡对比

输入数据：35, 37, 34, 56, 25, 62, 57, 9, 74, 32, 94, 80, 75, 100, 16,82

image-20200328004028606

图1-2

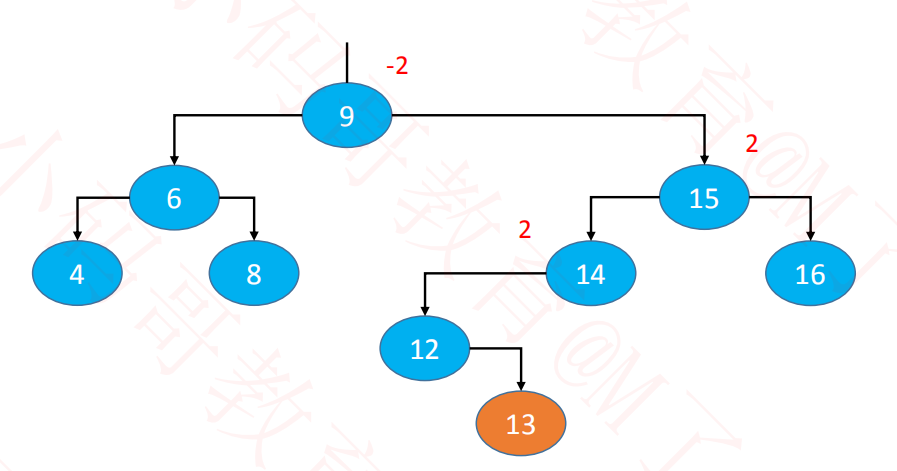
二、添加导致的失衡与解决方案

示例：往下面这棵子树中添加 13

最坏情况：可能会导致所有祖先节点都失衡

父节点、非祖先节点，都不可能失衡

image-20200328004334531

图2-1

1、LL – 右旋转（单旋）

image-20200328004903056

图2-2

2、RR – 左旋转（单旋）

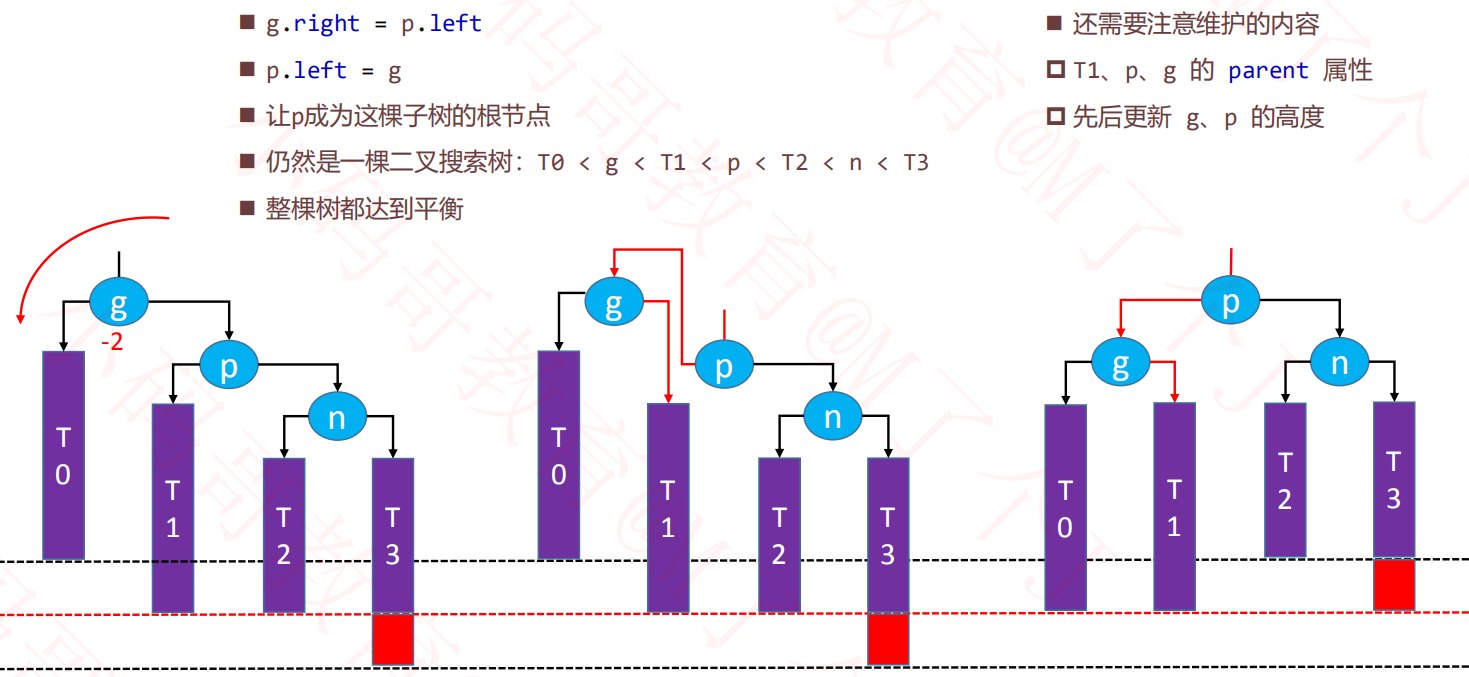
image-20200328004945370

图2-3

3、LR - RR左旋转，LL右旋转（双旋）

图2-4

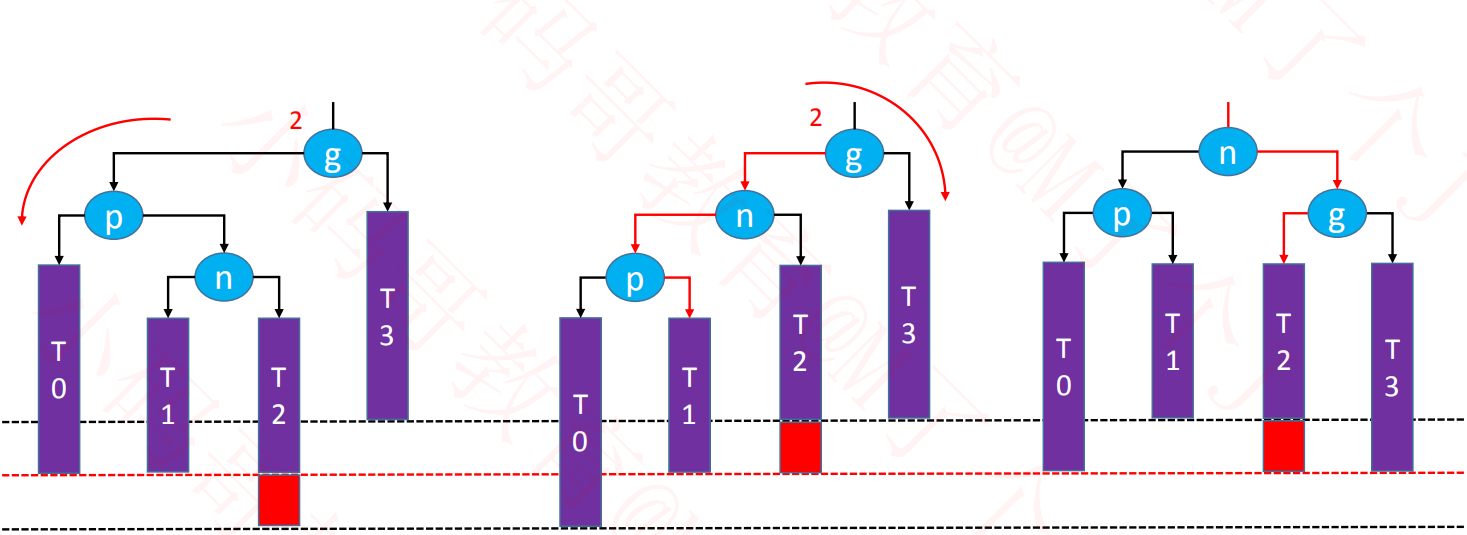
4、RL - LL右旋转，RR左旋转（双旋）

image-20200328005250371

图2-5

三、afterAdd实现

1、接口设计

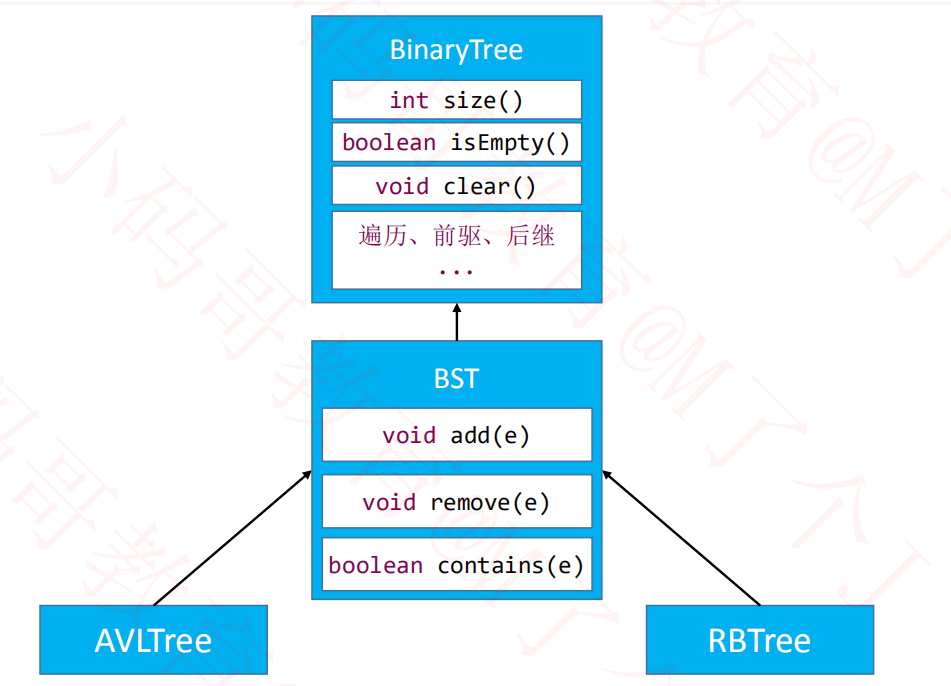
image-20200328011137233

图3-1 
    父类BST里面的空实现,AVL重写,实现afterAdd操作
	/**
     * 添加node之后的调整
     * @param node 新添加的节点
     */
    protected void afterAdd(Node<E> node) { }

1.1、修改创建Node的方式

BinaryTree:
    /*创建节点,取代直接new的操作,方便avl和rb调用父类操作*/
    protected Node<E> createNode(E element, Node<E> parent) {
        return new Node<>(element, parent);
    }

AVL:
	/*重写父类的方法,返回avl节点*/ //1创建avl节点,加一个height,avl节点由createNode创建
    @Override
    protected Node<E> createNode(Object element, Node parent) {
        return new AVLNode<>(element,parent);
    }

1.2、维护AVL自己的AVLNode

private static class AVLNode<E> extends Node<E> {
        int height = 1; //节点的高度

        public AVLNode(E element, Node<E> parent) {
            super(element, parent);
        }
    }

2、afterAdd

添加可能会导致是所有祖先节点失衡,只需要高度最低的失衡祖先节点恢复平衡即可 添加导致的失衡,只用进行O(1)级别的调整.

protected void afterAdd(Node<E> node) {
    while ((node = node.parent) != null) {
        //如果平衡,刚插入节点的高度是1是已知的,所以node.parent(1)=1+1,通过while循环总是能计算出`已平衡节点`的高度
        if (isBalanced(node)) {
            // 更新高度
            updateHeight(node);
        } else {
            // 恢复平衡
            rebalance(node); //
            // 整棵树恢复平衡
            break;
        }
    }
}

2.1、计算平衡因子

AVLNode:
//计算平衡因子 
public int balanceFactory(){
    //左子树
    int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
    //右子树
    int rightHeight = right == null ? 0 :((AVLNode<E>)right).height;
    // 1 0 -1三种
    return leftHeight - rightHeight;
}

2.2、节点平衡

private boolean isBalanced(Node<E> node){
    return Math.abs(((AVLNode<E>) node).balanceFactory()) <= 1;
}

2.3、更新高度

更新高度的思路:
新增的节点它一定是一个子节点,子节点的高度默认就是1,所以每增加一个节点,在没有失衡的情况下
更新的其实的node.parent.parent...高度,一直会更新到root.
    2
1       3
例如上面的例子:
a.先添加2,2.height=1;
b.然后2.left添加1,1.height=1,node.parent!=null 更新高度,2.height=2.left.height+1=2
c.然后root.right添加3,3.height=1,node.parent!=null 更新高度,此时左右子树高度相等(默认返回左子树高度),2.height=2.left.height+1=2

AVLNode:
/*插入的节点肯定是一个叶子节点,节点的高度为它子树的高度+1,所以刚插入节点的高度就是1*/
public void updateHeight(){
    //左子树
    int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
    //右子树
    int rightHeight = right == null ? 0 :((AVLNode<E>)right).height;
    height = Math.max(leftHeight, rightHeight) + 1;
}

private void updateHeight(Node<E> node) {
    ((AVLNode<E>)node).updateHeight();
}

2.4、恢复平衡

#1.

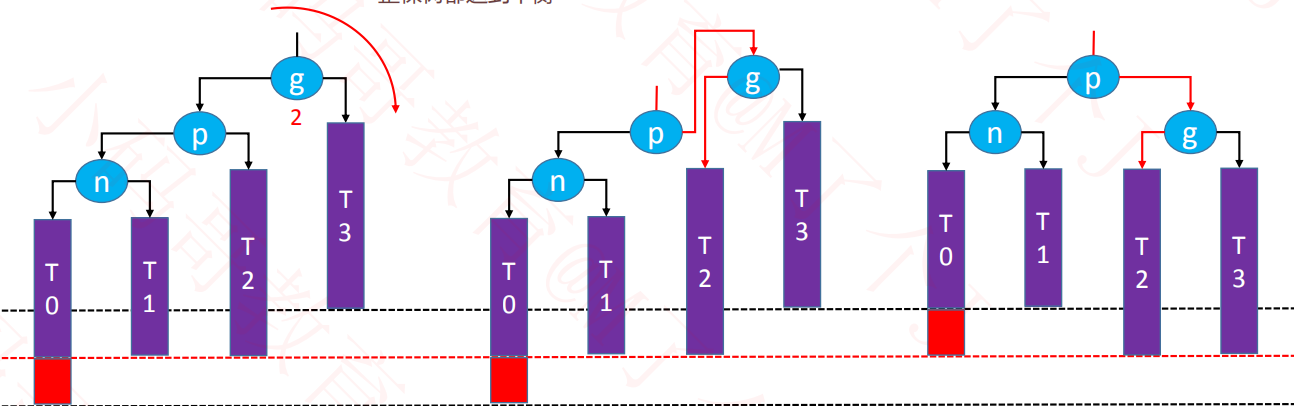
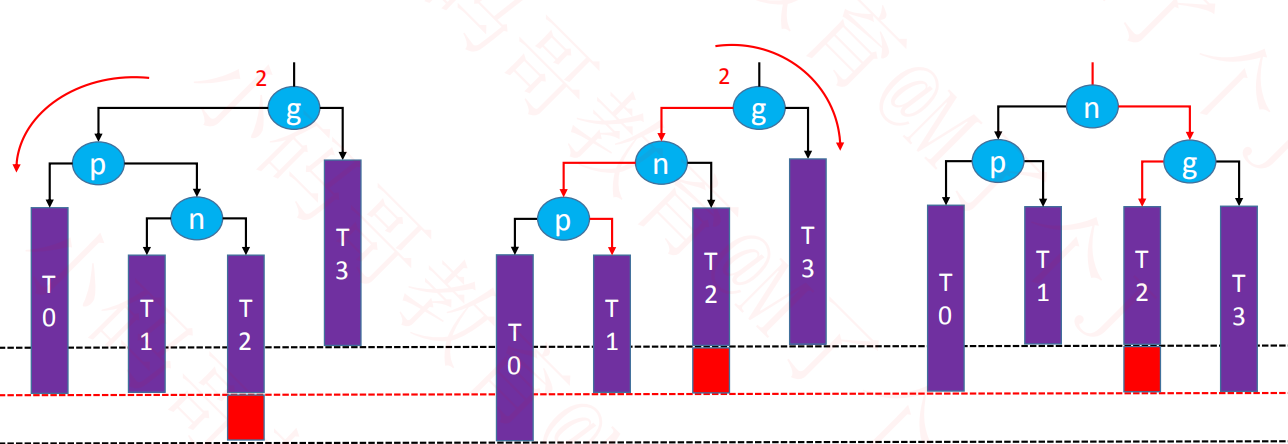
image-20200328173842080

图3-2

#2.

image-20200328173924601

图3-3

#3.

image-20200328173959095

图3-4

#4.

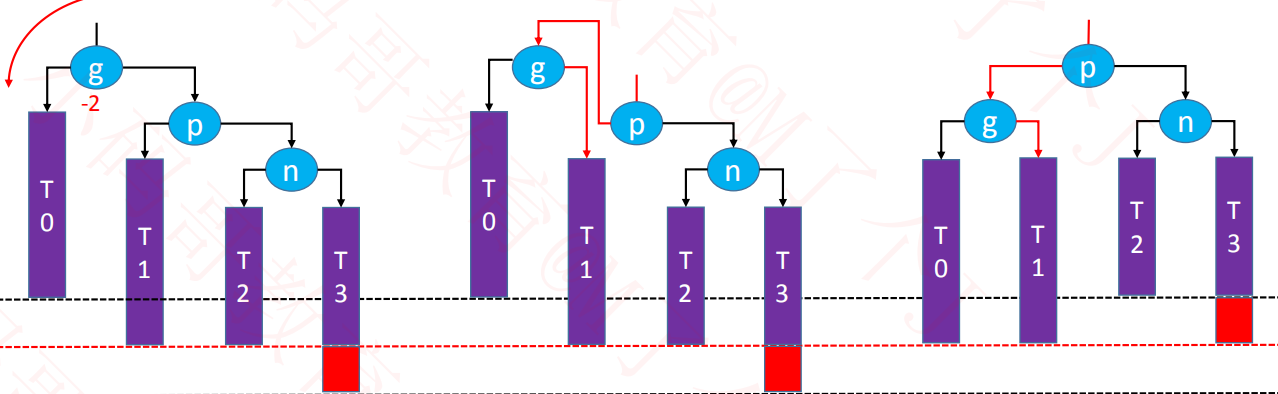
image-20200328174037481

图3-5 
/*grand为高度最低的不平衡节点*/
private void rebalance(Node<E> grand) {
    // 找p,grand左右子树最高的节点
    Node<E> parent = ((AVLNode<E>)grand).tallerChild();
    // 找node,p左右子树最高的节点
    Node<E> node = ((AVLNode<E>)parent).tallerChild();

    //判断是那种情况
    if (parent.isLeftChild()){ //L
        if (node.isLeftChild()){ // LL 右旋 #1
            rotateRight(grand);
        }else { // LR
            rotateLeft(parent);  //先对parent左旋#2
            rotateRight(grand);  //再对grand右旋
        }
    }else { //R
        if (node.isLeftChild()){ //RL
            rotateRight(parent);  //先对parent右旋 #3
            rotateLeft(grand);   //在对grand
        }else{ //RR
            rotateLeft(grand); // #4
        }
    }
}

2.5、找左右子树最高的节点

AVLNode:
public Node<E> tallerChild(){
    //左子树
    int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
    //右子树
    int rightHeight = right == null ? 0 :((AVLNode<E>)right).height;

    if (leftHeight > rightHeight) return left;
    if (leftHeight < rightHeight) return right;
    return isLeftChild() ? left : right ; //默认返回left...
}

2.6、左旋

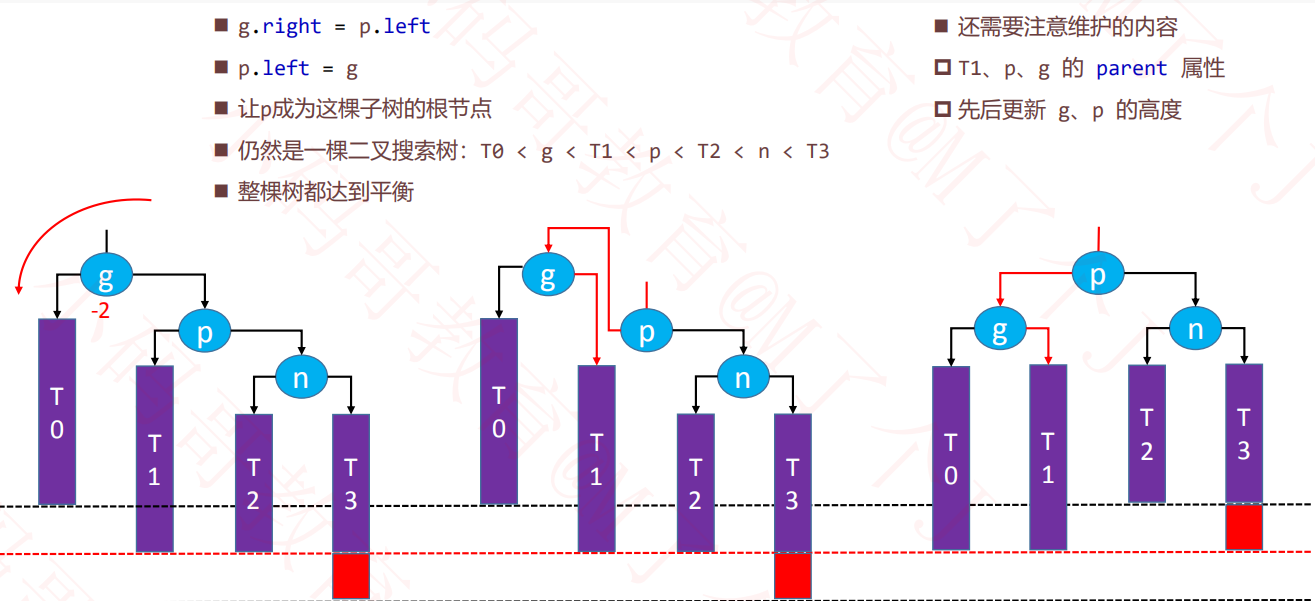
image-20200328174213675

图3-6 
private void rotateLeft(Node<E> grand) {
    //获得p节点,一定在g的右边
    Node<E> p = grand.right;
    //获得child节点,一定在p的左边
    Node<E> child = p.left;

    //旋转
    grand.right = child;
    p.left = grand;
    
    //旋转之后的维护
    afterRotate(grand, p, child);
    
//--------------------------------------
/*    //让p成为这棵子树的根节点
    p.parent = grand.parent;
    if (grand.isLeftChild()){
        p.parent.left = p;
    }else if (grand.isRightChild()){
        p.parent.right = p;
    }else { //grand为根节点
        root = p;
    }

    //维护child的parent
    if (child != null) {
        child.parent = grand;
    }

    //维护grand的parent
    grand.parent = p;

    //更新grand,p的高度
    updateHeight(grand);
    updateHeight(p);*/
}

2.7、右旋

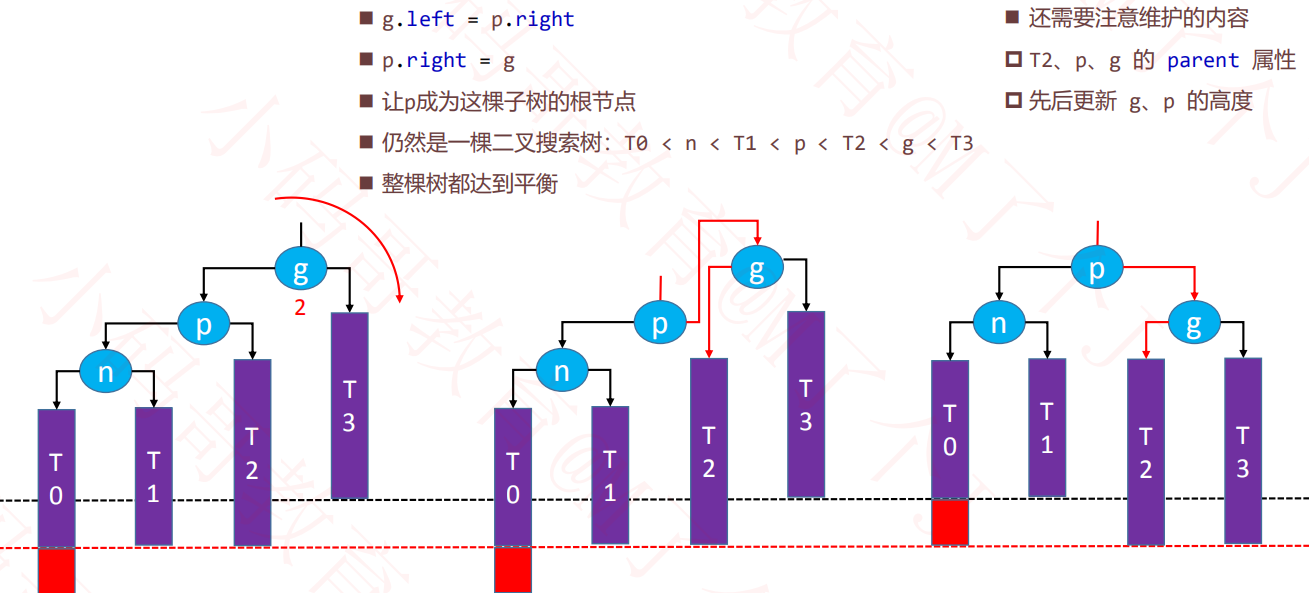
image-20200328174318860

图3-7 
private void rotateRight(Node<E> grand) {
    Node<E> p = grand.left;
    Node<E> child = p.right;

    //旋转
    grand.left = child;
    p.right = grand;
    
    afterRotate(grand, p, child);
    
//--------------------------------------
/*    //让p成为这棵子树的根节点
    p.parent = grand.parent;
    if (grand.isLeftChild()){
        p.parent.left = p;
    }else if (grand.isRightChild()){
        p.parent.right = p;
    }else { //grand为根节点
        root = p;
    }

    //维护child的parent
    if (child != null) {
        child.parent = grand;
    }

    //维护grand的parent
    grand.parent = p;

    //更新grand,p的高度
    updateHeight(grand);
    updateHeight(p);*/
}

2.8、旋转后维护关系

左旋或右旋后,维护p grand child的parent和更新高度都是统一的代码,所以可以提出来.

private void afterRotate(Node<E> grand, Node<E> parent, Node<E> child) {
    p.parent = grand.parent;
    if (grand.isLeftChild()){
        p.parent.left = p;
    } else if (grand.isRightChild()) {
        p.parent.right = p;
    } else {
        root = p;
    }

    if (child != null) {
        child.parent = grand;
    }

    grand.parent = p;

    updateHeight(grand);
    updateHeight(p);
}

2.9、打印avl节点:显示parent和height

BinaryTree:
public Object string(Object node) {
    /*E p = ((Node<E>) node).parent != null ? ((Node<E>) node).parent.element:null;
        return ((Node<E>) node).element+"_P("+ p +")"+height();*/
    return node; //方便avl树打印高度.
}

AVLNode:
public String toString() {
    E p = parent != null ? parent.element:null;
    return element+"_P("+ p +")"+"`h:"+height;
}

2.10、统一旋转

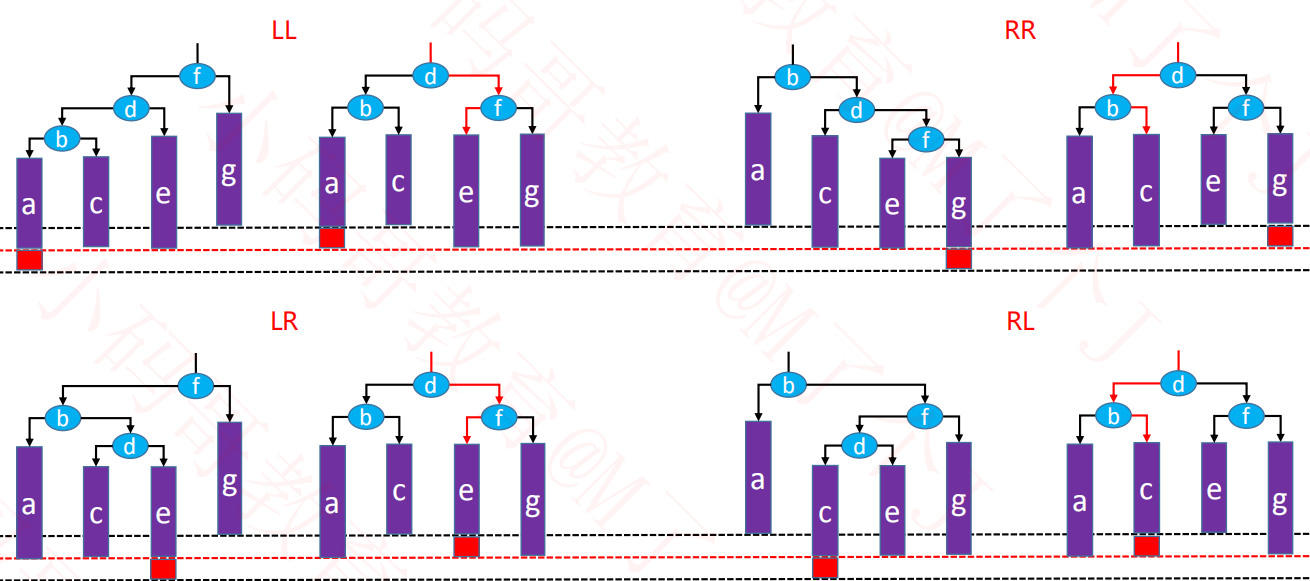
image-20200328223114244

图3-8

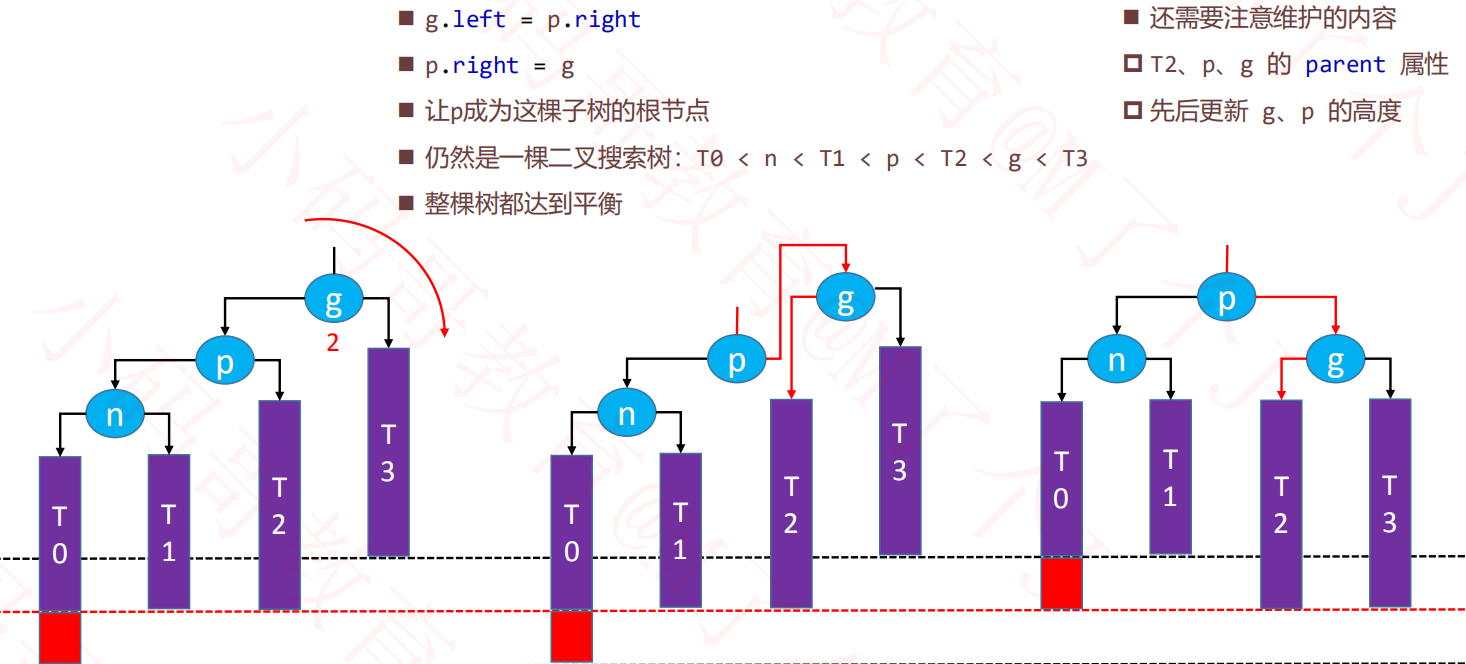
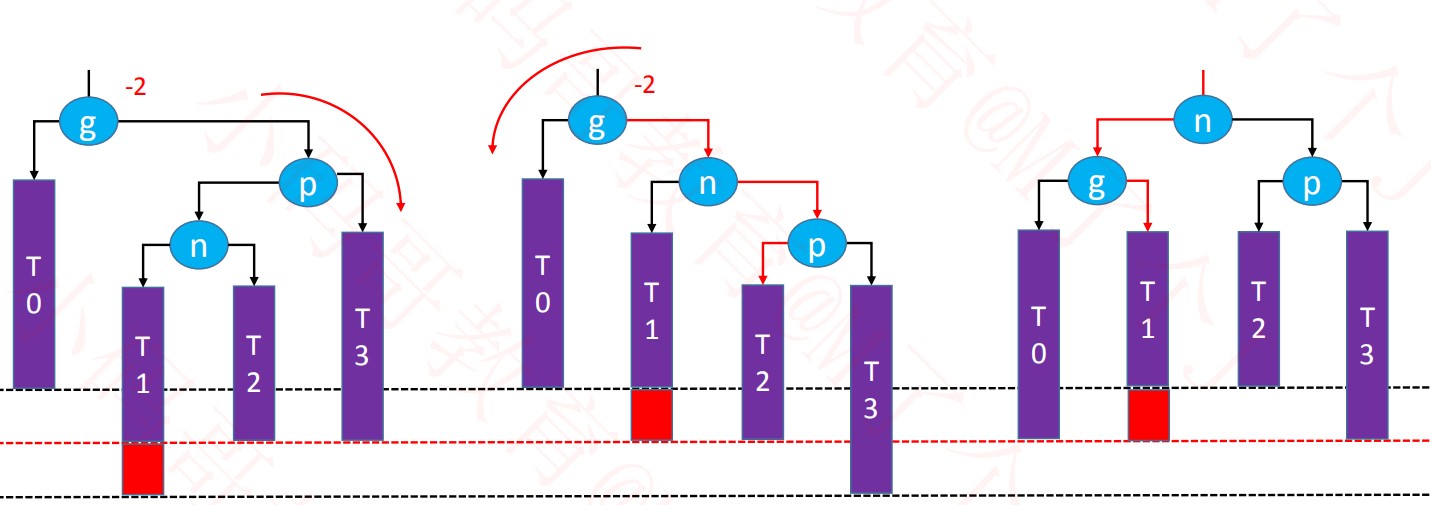
==可以发现每种类型的失衡状况经过旋转后得到的结果都是统一的==那么旋转操作逻辑可以整合成一段通用的代码逻辑.传入的参数可以对照LL、LR、RR、RL往里面套，a-g是从小到大排列的 。

private void rebalance(Node<E> grand) {
    // 找p,grand左右子树最高的节点
    Node<E> parent = ((AVLNode<E>)grand).tallerChild();
    // 找node,p左右子树最高的节点
    Node<E> node = ((AVLNode<E>)parent).tallerChild();

    //判断是那种情况
    if (parent.isLeftChild()){ //L
        if (node.isLeftChild()){ // LL
            rotate(grand, node.left, node, node.right, parent, parent.right, grand, grand.right);
        }else { // LR
            rotate(grand, parent.left, parent, node.left, node, node.right, grand, grand.right);
        }
    }else { //R
        if (node.isLeftChild()){ //RL
            rotate(grand, grand.left, grand, node.left, node, node.right, parent, parent.right);
        }else{ //RR
            rotate(grand, grand.left, grand, parent.left, parent, node.left, node, node.right);
        }
    }
}

统一旋转:a-g对应==图3-8==

    private void rotate(Node<E> r,
                        Node<E> a, Node<E> b, Node<E> c,
                        Node<E> d,
                        Node<E> e, Node<E> f, Node<E> g){
        //让d成为这颗子树的根节点
        d.parent = r.parent;
        if (r.isLeftChild()) {
            r.parent.left = d;
        } else if (r.isRightChild()) {
            r.parent.right = d;
        } else { //r为根节点
            root = d;
        }

        //串a-b-c
        b.left = a;
        if (a != null) a.parent = b;
        b.right = c;
        if (c != null) c.parent = b;
        updateHeight(b);

        //串e-f-g
        f.left = e;
        if (e != null) e.parent = f;
        f.right = g;
        if (e != null) e.parent = f;
        updateHeight(f);

        //串b-d-f
        d.left = b;
        d.right = f;
        b.parent = d;
        f.parent = d;
        updateHeight(d);
    }

2.11、统一旋转优化

通过==图3-8==可以发现a一直是b的左子树，g一直是f的右子树，所以这两个不需要维护。

**注意:**在AVL树里面可以不维护，在其他数据结构可能要维护。

private void rebalance(Node<E> grand) {
    // 找p,grand左右子树最高的节点
    Node<E> parent = ((AVLNode<E>)grand).tallerChild();
    // 找node,p左右子树最高的节点
    Node<E> node = ((AVLNode<E>)parent).tallerChild();

    //判断是那种情况
    if (parent.isLeftChild()){ //L
        if (node.isLeftChild()){ // LL
            rotate(grand, node, node.right, parent, parent.right, grand);
        }else { // LR
            rotate(grand, parent, node.left, node, node.right, grand);
        }
    }else { //R
        if (node.isLeftChild()){ //RL
            rotate(grand, grand, node.left, node, node.right, parent);
        }else{ //RR
            rotate(grand, grand, parent.left, parent, node.left, node);
        }
    }
}

private void rotate(Node<E> r,
                    Node<E> b, Node<E> c,
                    Node<E> d,
                    Node<E> e, Node<E> f){
    //让d成为这颗子树的根节点
    d.parent = r.parent;
    if (r.isLeftChild()) {
        r.parent.left = d;
    } else if (r.isRightChild()) {
        r.parent.right = d;
    } else { //r为根节点
        root = d;
    }

    //串b-c
    b.right = c;
    if (c != null) c.parent = b;
    updateHeight(b);

    //串e-f
    f.left = e;
    if (e != null) e.parent = f;
    updateHeight(f);

    //串b-d-f
    d.left = b;
    d.right = f;
    b.parent = d;
    f.parent = d;
    updateHeight(d);
}

四、删除导致的失衡与解决方案

示例：删除子树中的 16

可能会导致==父节==点或==祖先节点==失衡（只有1个节点会失衡），其他节点，都不可能失衡

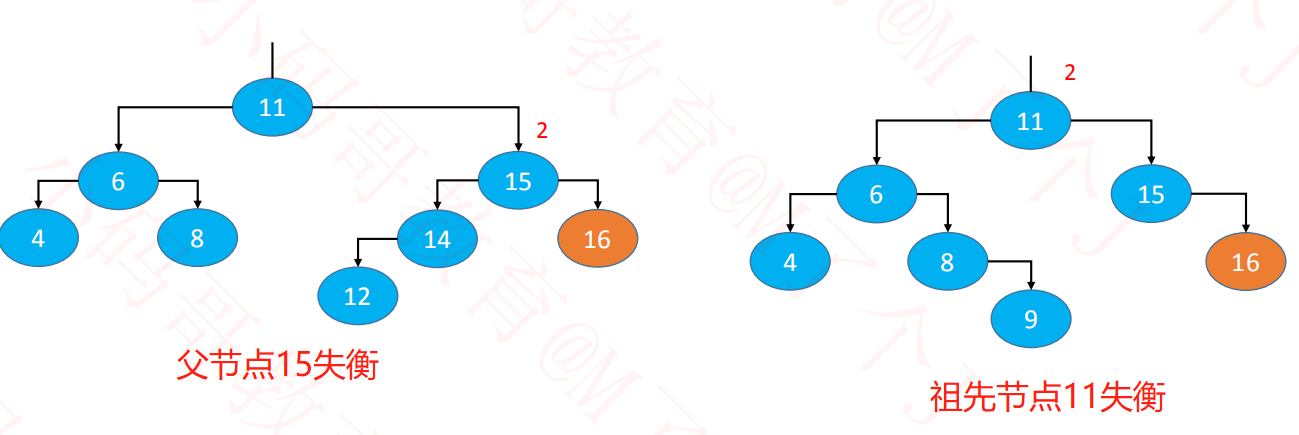
image-20200328234641981

图4-1

  • 如果绿色节点不存在，更高层的祖先节点可能也会失衡，需要再次恢复平衡，然后又可能导致更高层的祖先节点失衡...

  • 极端情况下，所有祖先节点都需要进行恢复平衡的操作，共 O(logn) 次调调整

1、LL – 右旋转（单旋）

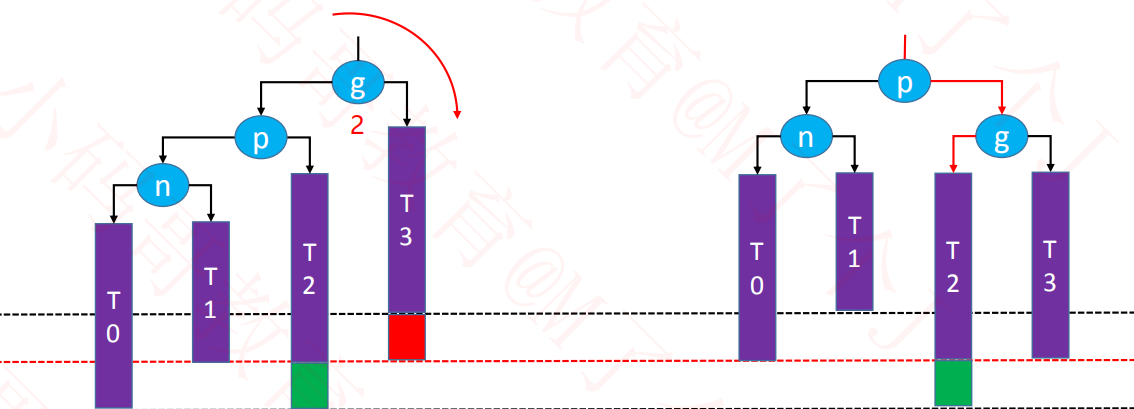
image-20200328234952638

图4-2

2、RR – 左旋转（单旋）

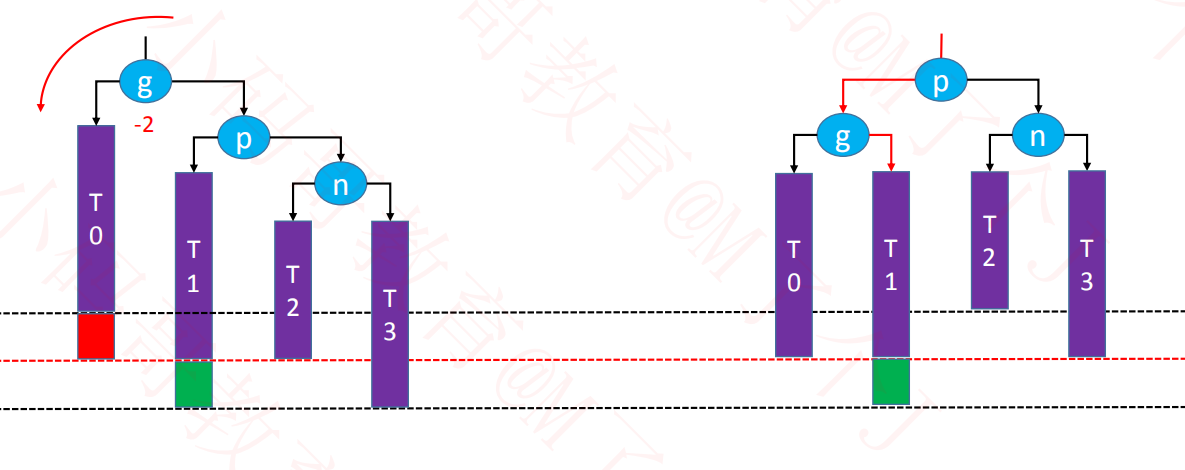
image-20200328235132630

图4-3

3、LR - RR左旋转，LL右旋转（双旋）

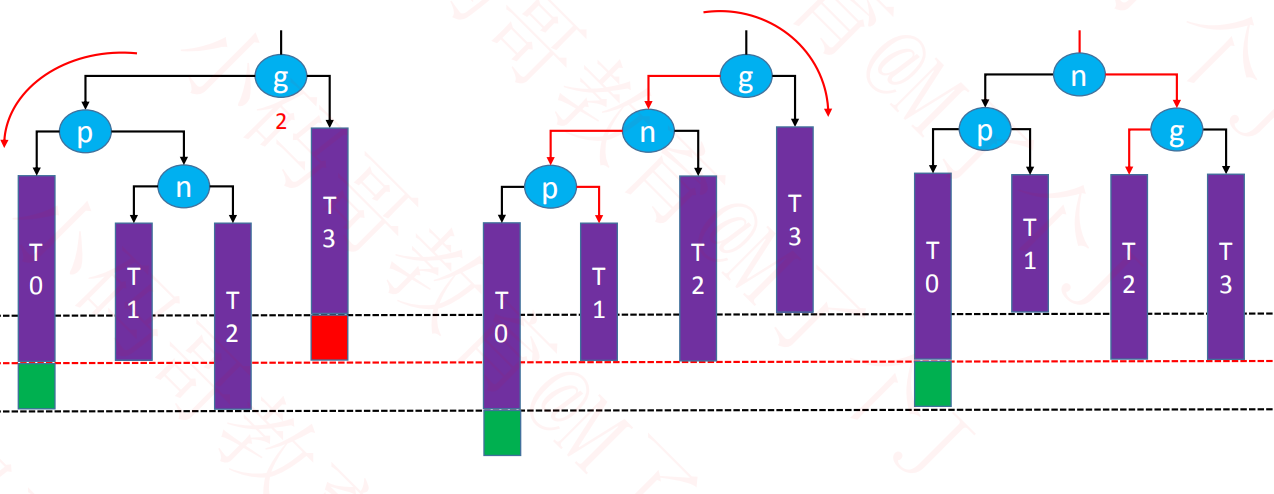
image-20200328235150010

图4-4

4、RL - LL右旋转，RR左旋转（双旋）

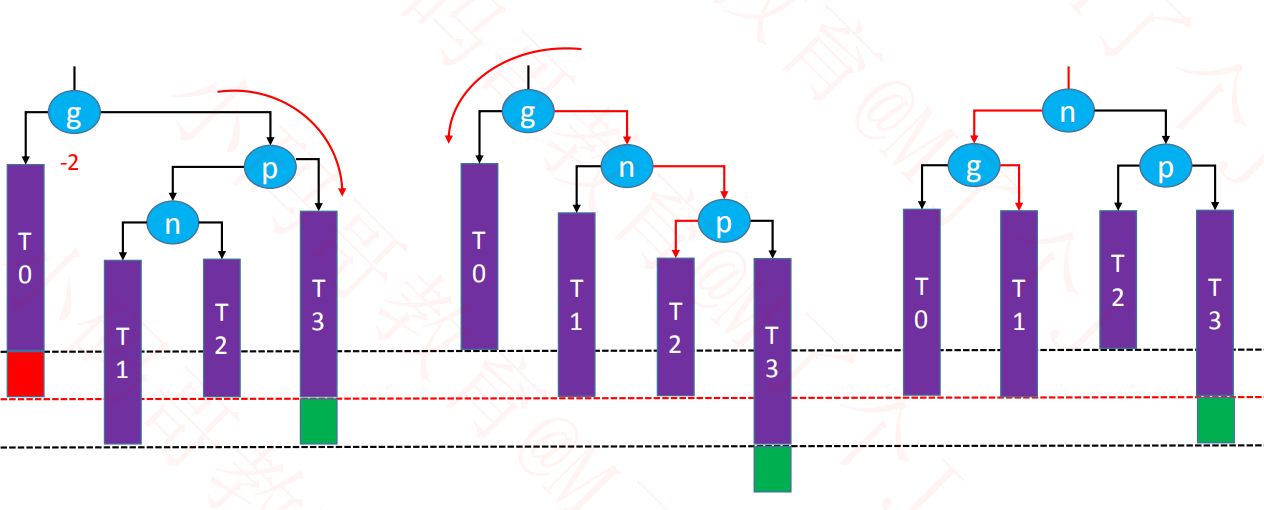
image-20200328235200672

图4-5

五、afterRemove实现

1、接口设计

父类BST里面的空实现,AVL重写,实现afterRemove操作
/**
  * 删除node之后的调整
  * @param node 新添加的节点
  */
protected void afterRemove(Node<E> node) { }

2、何时执行 afterRemove()

删除节点分为三种情况:

  1. 度为2

    删除度为2的节点，就是间接删除他的==前驱==或==后继==，所以afterRemove放在#a处是不合适的

  2. 度为1

    删除度为1的节点，就是让他的父亲节点的left或right指向他的子节点

  3. 度为0

    让他的父亲节点的left或right指向null

综上所诉，应该在#b、#c、#d处执行afterRemove（） 。

**补充：**在#e处其实也行，但这只针对AVL树，对红黑树来说#b、#c、#d处传递的参数可能都不一样。

private void remove(Node<E> node) {
        if (node == null) return;
        size--;
         ....
        //afterRemove(node); #a.
             
        // 删除node节点（node的度必然是1或者0）
        Node<E> replacement = node.left != null ? node.left : node.right;

        if (replacement != null) { // node是度为1的节点
            // 更改parent
            replacement.parent = node.parent;
            // 更改parent的left、right的指向
            if (node.parent == null) { // node是度为1的节点并且是根节点
                ...
            } else if (node == node.parent.left) {
                ...
            } else { // node == node.parent.right
                ...
            }
            //删除节点后,它父节点已经不指向它了,但是他的内部还保留指向它父节点的指针.
            afterRemove(node); //#b
        } else if (node.parent == null) { // node是叶子节点并且是根节点
                ...
            afterRemove(node); //#c
        } else { // node是叶子节点，但不是根节点
            if (node == node.parent.left) {
                ...
            } else { // node == node.parent.right
                ...
            }
            afterRemove(node); //#d
        }
    	 afterRemove(node); //#e
    }

3、afertRemove

删除节点后,可能导致父节点或祖父节点失衡,恢复平衡后,可能导致更高层的祖先节点失衡 最多需要O(logn)次调整

protected void afterRemove(Node<E> node) {
    while ((node = node.parent) != null) {
        if (isBalanced(node)) {
            // 更新高度
            updateHeight(node);
        } else {
            // 恢复平衡
            rebalance(node);
            //break; 不能中断,需要一直向上验证祖先节点是否失衡
        }
    }
}

六、总结

  • 添加

    • 可能会导致所有祖先节点都失衡
    • 只要让高度最低的失衡节点恢复平衡，整棵树就恢复平衡【仅需 O(1) 次调整】

  • 删除

    • 可能会导致父节点或祖先节点失衡（只有1个节点会失衡）
    • 恢复平衡后，可能会导致更高层的祖先节点失衡【最多需要 O(logn) 次调整】

  • 平均时间复杂度

    • 搜索：O(logn)
    • 添加：O(logn)，仅需 O(1) 次的旋转操作
    • 删除：O(logn)，最多需要 O(logn) 次的旋转操作
avatar
文章
阅读
粉丝